浅谈如何通过构建生活实践情境实现数学建模能力

高咏咏

摘 要：聚焦2020年高考试题，数学试卷上出现钢琴黑白键这一现象引起了广泛讨论。如何应对高考试题创新中出现的变数再次成为热议话题。文章将回顾历年高考及模考数学真题中的“乐理题”，分析其具体知识考查重点，并试图指出：高考题中音乐题频繁出现，恰恰是落实1952年以来，教育部课程标准对“注重数学文化的渗透，提升学生应用数学解决实际问题的能力”这一条标准的要求。对数学建模思想应用于生活艺术诸领域的考察，正是对数学核心素养的考查。对此，我们应该着重培养灵活运用高中数学基础知识的能力，锻炼学生在生活实践情境中解决数学问题的能力，培养学生的学科意识与问题关切。

关键词：高考数学;音乐与数学;数学建模

聚焦2020年高考试题，数学试卷上出现钢琴黑白键这一现象引起了广泛讨论。媒体纷纷评论：“从小学钢琴的孩子有福了。”从一方面看，这种说法固然有其合理性，加强对中学学生的美学教育不但是教育部推进素质教育改革发展的要求，也是时代发展的必然趋势。另一方面，这种说法也必然会引起另一个问题：难道不会钢琴的孩子就一定做不出这道高考数学题吗？答案当然是否定的。如果我们进一步深入分析命题人的出题思路，我们就会发现：高考题中音乐题频繁出现，事实上是对将数学建模思想应用于生活实践情境能力的考查，这并不强求学生具备相关的乐理知识。

需要进一步澄清的是：音乐与数学并非两个毫不相干的学科，恰恰是数学建模思维的发展，赋予我们认识文化生活实践诸领域一个新的维度。因而，高考试题中出现乐理题并不是出人意料的超纲，而恰恰是教育部课程标准对“注重数学文化的渗透，提升学生应用数学解决实际问题的能力”这一条标准的要求。面对高考数学试题的创新沿革，我们需要担忧的恰恰不是“如何补充领域外的知识来应对考查范围的变数”，而是如何用数学建模思维统摄生活中的杂多。简而言之便是：用数学思想渗透生活实践，数学不仅仅在试题本上，也在生活中。对数学建模思想应用于生活艺术诸领域的考查，正是对数学核心素养的考查。

同时，我们也需要意识到，2020全国2卷文科高考数学题中出现乐理题，或者更宽泛地来说，高考数学题中出现与艺术美育相关的题，并不是一个个别现象。如果我们追踪五年内各省市高考题和模拟试题，我们会发现这种通过构建生活情境来检验学生数学思维能力与建模能力的考查思路与方法，在近几年数学考试命题中是一脉相承的。因此，在对高考数学进行准备复习工作时，我们聚焦题目考查的重点、方法与思路，培养学生在生活实践情境中灵活运用数学建模思维发现和解决问题的能力。

文章主要分为三个部分，首先，我们将回顾历年高考及模考数学真题，给出较为合理的解题方法，并分析其具体知识考查重点。其次，我们将进一步分析命题人的考查重点与考查思路对学生相应能力的要求。最后，我们将着眼于这些要求，探索如何针对这类题目的命题思路，培养学生的相关能力，以应对考试。

一、 试题解法分析

（一）2020全国卷二文科高考数学第3题分析

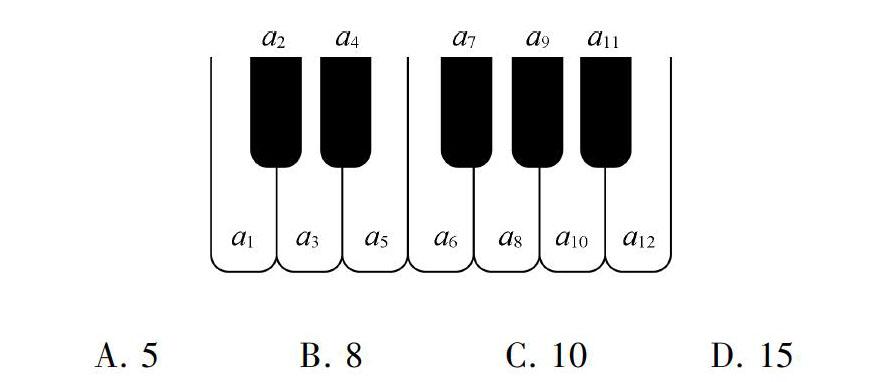
题目：如图，将钢琴上的12个键依次记为a1，a2…a12，设1≤i≤j≤k≤12，若k-j=3且j-i=4，则称ai，aj，ak，为原位大三和弦;若k-j=4且j-i=3，则称ai，aj，ak为原位小三和弦，用这12键可以构成原位大三和弦与原位小三和弦的个数为（  ）

A. 5

B. 8

C. 10

D. 15

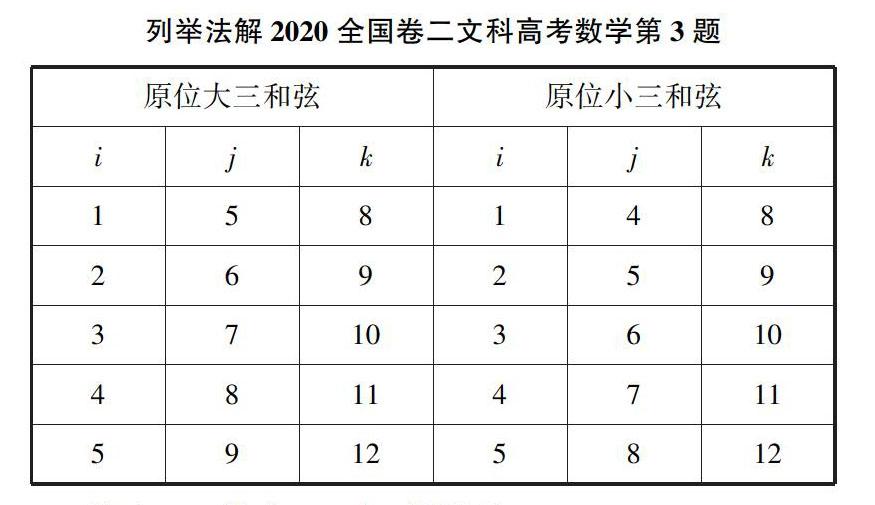
这道题目看上去较为抽象复杂，事实上用排列组合中的简单列举法就可以解出。

综上，一共有10个，答案选C。

如果学生有过学过键盘乐器的经验，确实容易对此类生活情境有着更直观的把握。但事实上，命题人在这里引入钢琴键盘，并不是为了考查学生的乐理知识，而是要考查学生在生活实践情境中灵活运用相关知识的能力。另一点需要澄清的是：要解答这道试题需要的并不是额外的乐理知识，事实上，解答这道题所需要的乐理知识已经以数学模型的方式在题目中表达了出来。更具体地说，命题人在题目中已经对黑白键进行了数学符号化，将原位大三和弦和原位小三和弦的定理用数学公式表达出来，为考生对陌生领域的把握提供了桥梁，因而已经将音乐问题转化成了数学问题。恰恰是通过数学桥梁的搭建，学生能够用最基础的排列组合知识，解决陌生领域的问题。

数学建模在生活情境中的运用远不止于此，《普通高中课程标准》中明确指出：“音乐的要素都与数学相关，特别是音的律制与数学的关系十分密切。”2018年北京高考数学第2题道选择题就精确贴合课程标准，考察了学生运用数学方法解决律制问题的能力。

（二）2018年北京高考数学第2题分析

题目：“十二平均律”是通用的音律体系，明代朱载堉最早用数学方法计算出半音比例，为这个理论的发展做出了重要贡献。十二平均律将一个纯八度音程分为十二份，依次得到十三个单音，从第二个单音起，每一个单音的频率与它的前一个单音的频率的比都等于122，若第一个单音的频率为f，则第八个单音的频率为（  ）

A. 32f

B. 322f

C. 1225f

D. 1227f

這道题是建立了等比数列模型，需要运用的基础知识点是幂指数的运算，是高中数学必修一的基础知识点之一。如果说上一题是在生活情境之上构建数学模型，那么这道题则是与音乐领域用数学表达的既有范式有关。作为给乐器人声调音校准的范式，五度相生律、纯律、十二平均律等律制的演变革新恰恰与人类历史上数学的进展密切相关。培养学生的学科意识和学科关切，扩展学生的学科视野近些年愈发被重视，因此，音乐与数学模块作为D类选修课程变得愈发重要起来。

以上选择的两道题目都是高考数学试题中出现乐理题的典型案例。事实上，回溯历年高考数学及模拟真题，有不少试题涉及音乐及相关艺术文化实践场景。选择这两道题目作为示例的原因是：首先，这两道题目均为高考真题，在一定程度上代表了近几年高考命题的命题思路和方向;其次，这两道试题较好地体现了数学与音乐深度结合的思路。在第一道题中，命题人用数学建模的方法较为精简准确地概括了抽象的和声学知识，将黑白琴键数字化、符号化，不仅符合课程标准规定的考察重点，也切实符合当代音乐研究的发展方向。在第二道题中，命题人用短短几十字揭示了数学科学发展与律学变革的关系，体现了命题人相当精深数学科学史素养，这种历史的跨学科思维与素养是近年来中学数学教育新的侧重点。