利用Tracker软件研究扭摆的振动

王 林 肖桂娜 耿钰超

(上海师范大学数理学院 上海 200234)

研究扭摆振动是大学物理实验的重要内容，扭摆实验是利用光电门传感器测量扭摆振动周期，此方法难以描绘扭摆的振动图像，而扭摆的振动图像是研究扭摆振动的重要步骤，通过振动图像能分析出扭摆在较长时间内的阻尼振动情况.

本文利用Tracker软件自动追踪功能，获得相应的数据与振动图像，利用数据分析功能，研究在短时间内扭摆的简谐振动，分析不同摆角对振动周期的影响，通过对长时间内扭摆振动进行图像拟合，研究扭摆阻尼振动规律，并且计算出阻尼系数.

1 实验原理

由于扭摆在振动的过程中受摩擦力矩与空气力矩的共同影响，扭摆在较长时间内的振动属于一种阻尼振动，这种力矩称为阻力矩.在振动角速度较小的情况下，可认为阻力矩的大小正比于扭摆的角速度大小，则阻力矩为

(1)

式中c为扭摆的阻力系数，扭摆在回复力矩与阻力矩的作用下，可得到

(2)

其中I为扭摆没有放置物体时的转动惯量，k为扭摆的扭转系数.在式(2)中将I除遍各项，得

(3)

令

(4)

式中ω0是扭摆振动系统的固有圆频率，β是振动的阻尼因数，将式(4)代入式(3)，可得

(5)

我们通过简单的实验可知，扭摆振动运动状态是欠阻尼状态，则式(5)的运动学方程为

(6)

其中A为扭摆振动的振幅，φ为振动的初相位，它们都是初始条件.通过式(6)可以看出扭摆运动的振幅Ae-β t是随时间的推移成指数的形式衰减的，最终衰减为零，整个振动则以ω1为圆频率做周期性变化.

由于扭摆的衰减较小，在短时间内扭摆的转动可以看成一个简谐振动，其回复力矩

Mc=-kθ

(7)

根据刚体的转动定理得

(8)

(9)

其中ω为扭摆振动的圆频率[1].

2 实验操作与数据采集

2.1 Tracker软件说明

Tracker软件属于一款视频跟踪操作分析软件，同时它还是面向物理教育的免费开源软件, Tracker软件解决了过去物体教学过程中只能观察物体运动过程而不能描绘出物体具体运动轨迹的问题，同时它还能对记录下的物体运动过程进行定量分析.通过视频拍摄技术将物体的运动过程记录下来，将其导入进Tracker软件中，利用Tracker软件中的定标、建立坐标系、自动追踪等功能，根据物体运动轨迹按原比例描绘图像，同时软件还可以记录每一个坐标点的速度、加速度、角速度、摆角等数据，利用Tracker软件中的数据拟合功能，观察实验曲线与我们的理论拟合曲线是否重合，从而来判断实验的准确性.同时在此过程中可以将物体的运动图像与数据提取出来进行分析.

2.2 实验操作

(1)将扭摆置于水平面上，并且调平.为了便于软件追踪，在扭摆的金属托盘摆动位置贴一个异于背景颜色的彩色纸片.实验装置如图1所示.

(2)本实验利用的是视频画质为4K,60 fps的数码相机或手机相机，笔者采用的是数码相机.将实验器材按图1摆放.这里最好能将相机放置在扭摆的正上方，这样能清晰地拍摄视频.将扭摆转至离平衡位置90°左右，松手并开始记录.

(3)将记录的视频导入Tracker软件中，建立坐标轴，将坐标原点放在托盘中心，竖轴与扭摆平衡位置重合.然后根据事先放好的实物长度定标，并隐藏坐标线与定标尺.

图1 研究扭摆振动实验装置图

(4)点击创建窗口，建立质点，然后按住Shift+Ctrl键选择标记带颜色的质点，拖动方框选择匹配区域，点击自动搜索，软件将会自动搜索出标记位置在不同时间内的坐标，根据需要将纵横坐标调整为摆角与时间的关系，如图2所示.同时可以得到在不同时间内摆角、角速度、角加速度大小等数据.

(5)数据点采集完成后，双击图进入图像数据处理界面，将图像调至合适大小，如图3所示.

(6)通过图3可看出扭摆的振幅在逐渐衰减，根据式(6)可知扭摆的振幅将随时间呈指数衰减，选择Tracker软件中的数据拟合的自定义公式，拟合包络线方程，在自定义公式的界面中编辑公式：θ=A*exp(-β*t)，手动调节变量，使包络线与实验图像的各个波峰相交，最终包络线的方程为:θ=1.6*exp(-0.026*t)，包络线图像如图4所示.

图2 质点追踪轨迹界面图

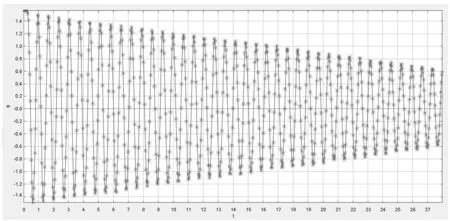
图3 实验散点连线图

图4 阻尼振动包络线图

(7)因为扭摆的振动是一个欠阻尼状态，阻尼因数应该小于1，由包络线方程可知，扭摆的阻尼因数为0.026 s-1，符合理论.根据式(6)可以编辑阻尼振动公式:θ=A*exp(-β*t)*cos(ωt+φ)，手动调节参数使拟合图像与实验图像吻合，如图5所示.

图5 振动拟合图像

图5中的方点为扭摆振动在不同时刻的位置数据点，实线曲线为扭摆振动的拟合图像，拟合函数为

θ=1.6e0.026tcos(9.054t-2.53)

(10)

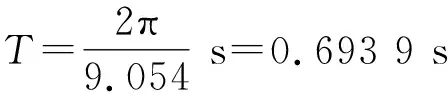
根据式(6)可知扭摆的振动圆频率理论值

(11)

而实验测量结果振动圆频率为9.054 rad/s，相对误差为0.871%，说明实验结果有效.

(8)双击坐标轴，用质点振幅与角速度建立阻尼振动的相图，如图6所示，通过图6可知，扭摆振动的相轨迹是椭圆，表示扭摆的振动随着时间的推移，旋转的振幅与最大角速度都在衰减，最终停止[2].

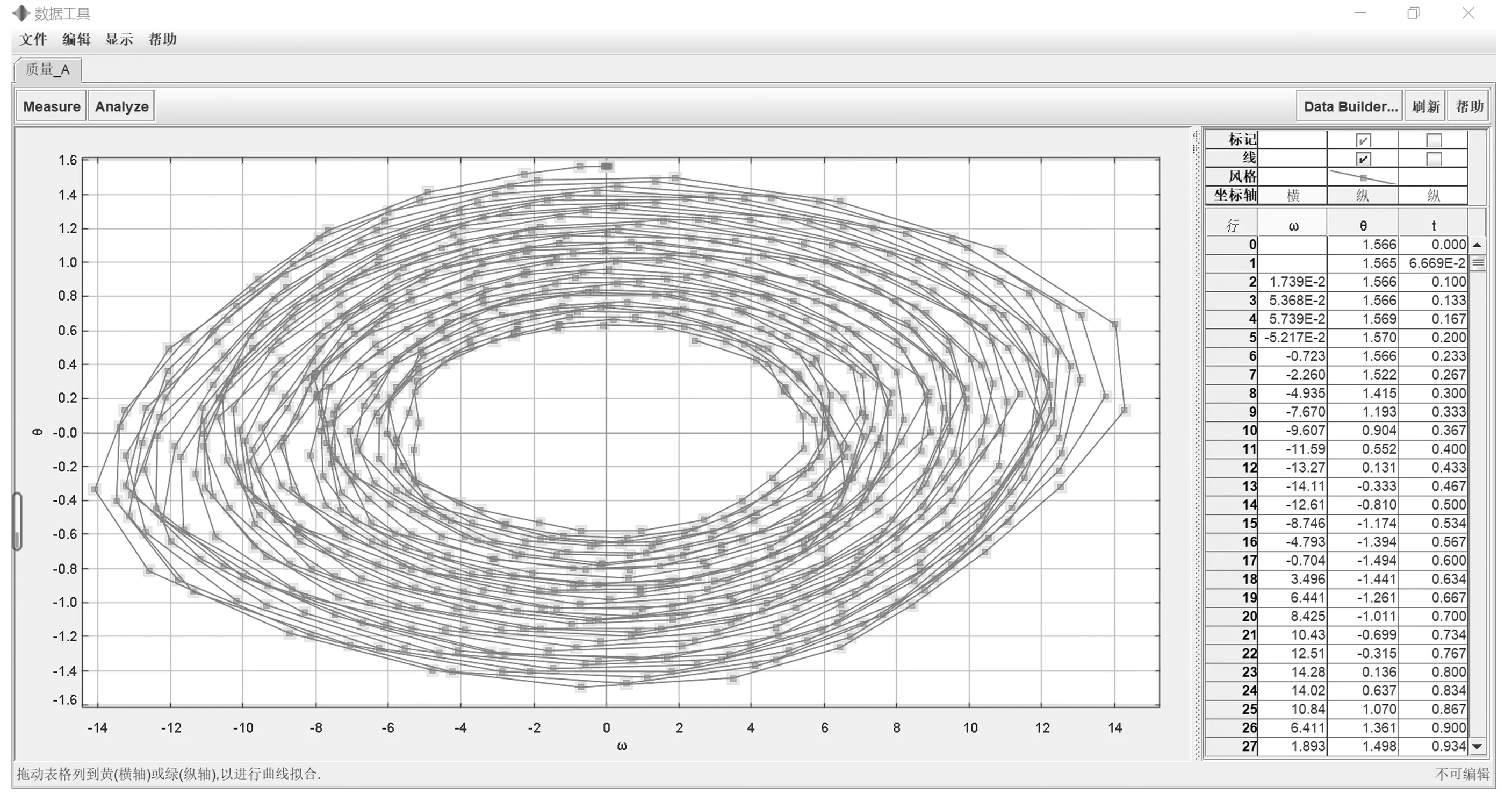
图6 阻尼振动相图

3 利用Tracker软件探究不同摆角对周期的影响

在扭摆振动实验中，一般要求在摆角为90°左右释放，扭摆摆角的大小对扭摆振动是否有影响？现在运用Tracker软件与光电门传感器两种方法探究不同的摆角对振动周期的影响，以光电门传感器测量的数据为标准，探究Tracker软件测量周期是否准确，同时观察摆角的不同是否会对周期产生影响.根据式(9)可知扭摆在短时间内的振动可以看成简谐振动.

按照上述实验操作，用视频记录摆角从20°～110°扭摆的振动过程，将记录的不同摆角的视频分别导入Tracker软件中.以30°摆角为示例，选择视频区域为两个周期左右，打开数据图像功能，点击数据拟合，编辑公式

θ=Acos(ωt+φ)

手动调整参数，使拟合函数与实验图像吻合，如图7所示.

图7 30°摆角的振动拟合图

由图可得拟合函数

θ=0.58cos(9.08t+0.2)

得到振动周期

采用同样的操作，利用Tracker软件测量摆角在20°～110°范围内其他角度的周期.

同时利用光电传感器也测量出摆角20°～110°范围的扭摆振动周期，统计用Tracker软件与光电门传感器测量的不同摆角的周期，如表1所示

表1中T0代表光电门传感器所测量的扭摆振动周期，T1代表Tracker软件所测量的扭摆振动周期，E表示相对误差.通过表格数据分析，光电门传感器所测量的振动周期方差小于1，可以得到振动的离散程度小，说明扭摆振动的摆角的大小对周期的影响可以忽略.以光电门传感器所测量的周期为理论值，Tracker软件测量的不同摆角的周期数据相对误差都小于1%，说明利用Tracker软件测量的扭摆振动周期精确度高.同时观测两种方法所测量不同摆角的振动周期大小变化太小，由此可以得出扭摆的摆角大小对周期的影响可以忽略.因此在实验过程中没有必要强调摆角是90°，只要摆角在摆动限度内，实验结果不会受到影响[3].

表1 Tracker软件与光电传感器记录不同摆角振动周期列表

4 结论

本文通过Tracker软件追踪功能研究分析扭摆的振动，根据软件中的数据分析功能得到拟合方程、包络线方程、相位图等.Tracker软件帮助实验者将不可描绘出来的运动轨迹可视化，使实验者更加清晰地了解扭摆的振动过程.同时实验者还可以通过手机记录运动过程，使实验更加地便捷与高效.通过Tracker软件研究扭摆振动的方法，操作简单、便捷、高效、实验结果精确度高，值得采用.