虎门大桥狮吼功和秋千*——有关共振之辩

李品钧

(湛江幼儿师范专科学校信息科学系 广东 湛江 524037)

2020年5月5日下午至6日中午，广东虎门大桥发生幅度较大的振动现象，一度为人们热议. 一般人可能不解，作为一座跨海大桥，经历了多次台风的攻击均岿然不动，为何这次在仅仅3～5级的风力(微风、和风和清劲风)作用之下发生了如此猛烈的振动现象？国内专家组最初认定这是一种由卡门涡街效应导致的共振现象. 具有中学物理知识背景的人都应该知道，如果是共振，那么风力的大小因素就要退居二线，而风力变化的周期或频率才是主因. 因为理论上只要周期性外力的变化频率与振动系统本身的固有频率相等，那么，尽管外力不是很大，只要随着时间的积累，振动系统的振幅将无限增加，直到振动幅度超过材料的承受极限而使其撕裂.

与此相关的事件最著名者莫过于美国塔科马(Tacoma)海峡大桥的风致垮塌事件，该桥自1940年7月1日开通运营，此后即使在微风作用之下，也时常有抖动，素有“会跳舞的桥”的美称. 4个月后的11月7日，当天风速19 m/s(8级，大风，对海滨城市来说是常见的风力，约为台风风力的一半).该桥在经历了70 min剧烈的震动之后最终达到形变极限而垮塌. 当时，一组好莱坞电影团队正好在桥的附近拍摄，他们将大桥从开始振动到垮塌的全过程拍了下来，塔科马海峡大桥借此抢了一众好莱坞大牌的戏[1].

除了对大型建筑物具有毁坏作用之外，共振对小型物件同样具有破坏性，前几年综艺节目上较为流行的“声音碎杯”的表演便是其中的典型.2015年江苏卫视《最强大脑第二季》第1期的节目上，一个名叫吕飞龙的表演者在不借助扩音设备的情况下5 s之内徒口喊碎红酒杯，令观众瞠目结舌，惊呼不可思议，不少人认为这可能就是传统武术中的“狮吼功”. 这一表演的真实性也在线上和线下产生了大量的争议，节目嘉宾高晓松甚至以他的“工学背景”这一身份坚称：“吕飞龙一定是使用了某种我们看不出来的别的办法.”

从这些争议中我们可以看到，知道共振现象的人很多，但了解共振的人其实很少. 共振的机理是什么？那么小的力作用为什么会有那么大的破坏力？能量还守恒吗？下面对这些问题进行类比分析并做一些定性半定量的计算，试图通过简单易懂的方法让读者对共振现象能有更深入和具体的了解.

1 秋千中蕴含的共振原理

秋千大致可以分为两类，一类为他助式秋千，另一类为自助式. 顾名思义，他助式秋千指的是荡秋千的时候一人坐在秋千板(或座椅)上，另一人在固定位置周期性地推动被荡者后背或秋千椅，只需规律性地推动几下，便可以将秋千荡得很高. 此后即便便不再施力推动，秋千也能维持较长时间的摆荡状态，此后摆幅越来越小最终悬停在最低点. 这个最低点我们称之为平衡点，秋千在摆动时总是在这个平衡点两侧做往复式运动，这种运动我们称之为振动. 注意到，秋千在平衡点的时候速度最大，因而拥有最大的动能；荡到最高点的时候速度为零，动能完全转化为重力势能. 如果没有空气和其他阻力，由于能量守恒，秋千将一直摇荡下去，能量周期性地在动能和势能之间转换并保持总量不变. 外加的推力使得秋千越荡越高，此时的振动叫做受迫振动，此推力叫做驱动力；撤掉外力，在空气阻力的作用之下，秋千将越荡越低. 像空气阻力这类消耗振动系统机械能的因素我们称之为阻尼，有阻尼存在时的振动叫做阻尼振动. 值得注意的是，并不是所有的外力都能够让秋千越荡越高，如果外力的变化毫无规律(通俗地讲就是施力节拍和秋千的振荡节拍不同)，秋千是不会很顺利地荡起来的. 只有当驱动力的施力周期和秋千的振荡周期相同时，秋千才能很快地荡起来而且荡得越来越高. 这种当驱动力的施力周期和系统振动周期相同时，驱动力总是与运动方向相同，做正功，振动系统的振幅越来越大(理论上可以是无限大)的现象就是一种共振现象.

自助式秋千由一块悬吊在两根吊绳(或链)上的踏板构成，荡秋千的时候无需他人辅助，仅一人站在踏板上通过有规律地伸展身体就可以将秋千逐渐荡起来并在短时间内荡到很高. 这种秋千的玩法比较讲求技巧性，不懂技巧的人任凭站在秋千板上怎么扭动挣扎，秋千也只会小幅度地摆动几下然后慢慢停下来. 但是只要掌握共振的原理，绝大多数人都可以很快地将秋千荡起来，这个原理就是上面所说的“驱动力施力周期与秋千的振荡同拍，总是保持施力方向与运动方向相同，做正功”. 荡秋千时用到的力是重力，练习者踏上秋千的时候可以通过用一只脚蹬踹地面或者晃荡一下身体形成一个微扰，秋千便会产生小幅度的振荡. 这时，练习者只需在每次秋千下降时将身体蹲下，此时体系重心向下移动，重力做正功，动能增加，势能减小，总机械能不变. 当秋千荡到最低点时迅速起身，此时体系的重心上移，但是重力方向与体系的运动方向垂直，因而对体系的动能无影响，但是势能增加了，于是总的机械能增加. 这样，当体系越过平衡点荡向对面的时候，就会达到一个新的高度. 一个振荡周期有两个下降过程，按照上述的方法操作，秋千每摆荡一个周期，高度就增加两次，几个回合下来，秋千就可以荡到比较高的高度了. 只要摆线足够长，阻尼足够小，哪怕每次只用一点点力，秋千的摆荡高度也会无限地增加下去.

2 弹簧振子受迫振动的定性半定量处理

上面我们通过秋千的振荡介绍了受迫振动和共振的概念，为了能在数量上对共振有一个更为具体的了解，我们现在考虑弹簧振子的共振，一根一端固定的弹簧，另一端连接一个质量为m的物体，就构成了一个弹簧振子. 当我们将一根弹簧拉伸或压缩，弹簧会产生一个指向平衡位置的回复力(弹力)，此回复力的大小和方向满足胡克定律f=-κx.当我们将一个弹簧振子拉伸以后再撤掉外力，那么，在回复力的作用之下弹簧会朝平衡位置运动，这时回复力与运动方向相同，做正功，振子的动能增加；到达平衡点时，速度达到最大值，受力为零，由于惯性作用，振子将继续朝着压缩弹簧的方向运动，弹力开始反向，振子速度逐渐减小，当速度减为零时，振子达到最大压缩量，然后在回复力的作用之下开始向着平衡位置运动……就这样，弹簧振子在回复力的作用之下振荡起来. 现在我们假设有某种周期性的外力施加在振子之上. 如果此外力的变化周期与振子的振动周期完全相等的话，在振子的“拉伸-恢复-压缩-恢复”4段运动过程中，它对振子所做的功都是正功，如果任由这个外力一直作用下去，振子的振幅将会越来越大越来越大，直到弹性失灵或弹簧被拉断. 这就是弹簧振子发生共振时造成破坏的原因.

为了让读者对弹簧振子的共振有一个更加具体一些的理解，这里建立一个简化的数学模型对此进行分析.假设某种周期性外力刚开始作用于振子时，使振子产生了0.001 mm的初始形变(力比较小，产生的初始形变肉眼根本看不到)，假设弹簧的弹性系数κ=1 000 N/m(相当于1 kg的物体只能将弹簧拉长1 cm, 可见弹性系数较大，较难发生形变)，根据胡克定律可以算出这个力的大小f=1 000×10-6N=10-3N. 弹簧一旦产生了一个初始形变，便会开始微弱地振动起来. 通常情况下，周期性外力的大小和方向都随时间而改变，上式计算出的力只能看作是力的平均效果. 为使计算简便，我们假设弹簧的4段运动过程中，力都取上面这个“平均值”，只是方向一直保持和振子的运动方向相同. 由于有外力的作用，振子的振幅时刻都在改变，这将导致驱动力在每个四分之一振动中的路程都不相同，计算变得复杂. 这里也做一个简化：将驱动力在一个振动周期内做功所带来的振幅的增加全部计入到下一振动周期，本振动周期内振动振幅近似不变. 显然，这样做的后果会使得驱动力的功被少计算了一部分，因而振动的振幅增长会比实际情况偏慢一些. 将初始形变记为x0，在接下来一个周期的4段运动中，驱动力所做的功为：ΔW1=f·4x0=4×10-9J，这个功使得振子的振幅变为x1. 由功能原理可得

(1)

代入已知数据，可算得x1=0.003 mm，用同样的方法可以计算x2，x3,…. 这些计算我们可以交给计算机程序来完成(例如输出振动1次到振动10次的振幅的mathematica代码为：x=0.000 001; Do[x=((500.*x^2+4.*0.001*x)/500.)^0.5; Print[x],{i,10}]). 计算的结果如表1所示. 从该表我们可以看到，很小的力作用造成了小到肉眼看不见的初始振动，但只要保持驱动力周期与体系振动周期相同，振幅将不断增大，例如振动到300次的时候，振幅增长为1 mm左右. 振动到5 000次的时候，振幅增长为2 cm左右.

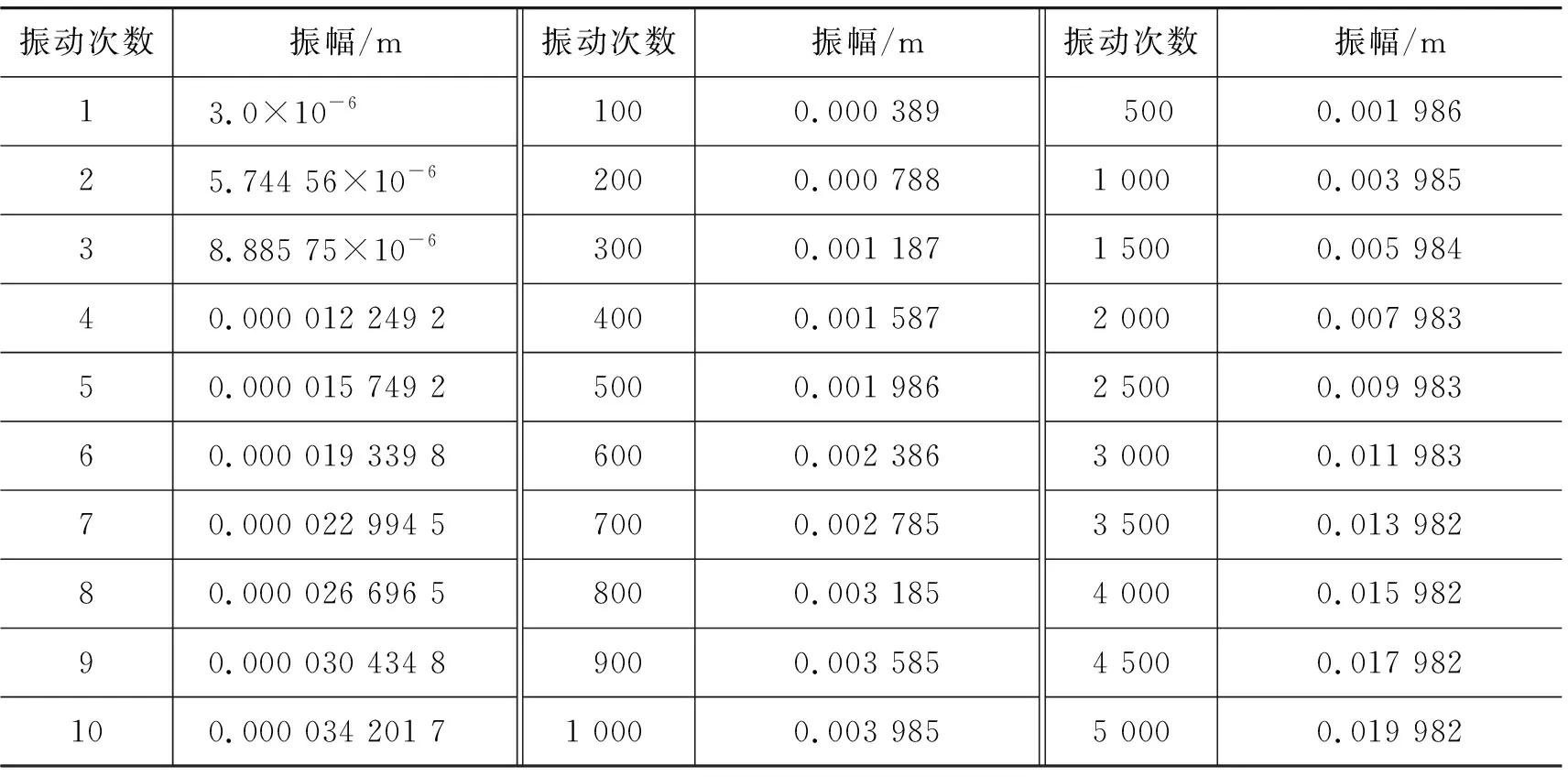
表1 振子的共振次数与振幅

3 共振的破坏性及其与颤振的区别和联系

很多物体在外力的作用之下都会发生振动，例如前面提到的虎门大桥和塔科马海峡大桥. 另外，在沿海城市，台风来临时，甚至可以肉眼看到高楼在风中摇摆(高楼层的人家可以明显感觉到较大幅度的摇晃)，电视剧里旧社会的人们采用这样的方式辨别银元(大洋)的真伪：用手指掐住银元，对着嘴巴使劲一吹，真的银元会发出很有质感的嗡嗡声，并且这声音可以维持较长的一段时间. 这就是利用了银元在气流的作用之下会振动而且这振动还能维持较长的时间，从这点可以看出，由空气产生的阻尼比较小. 高脚红酒杯的杯壁较薄，用手指轻叩杯壁或对着它用力哈气，也可以让它发出持续的嗡嗡声. 这表明红酒杯的杯壁也容易在外力的作用之下发生振动. 无论是桥梁、高楼等大型建筑物，还是银元、红酒杯等普通的物件，它们在流体(例如空气)中的受力情况和振动情况的精确计算都要依赖于复杂的建模，计算工作量大而复杂.

如果只是定性地理解这些物体振动的机制，我们仍然可以借助弹簧振子模型，只不过要将弹簧的拉伸和压缩推广到任意形式的“形变”，例如大桥在风力作用之下产生的扭曲和蛇形起伏. 又例如，用较高速的摄像机可以观察到，当受到适当频率的声音的作用时，红酒杯的杯口在声波的作用之下会交替地在两个垂直的方向上被“挤压”成椭圆形，从而形成一种“花式振动”，如图1所示. 下面我们重点谈谈风力作用下桥梁的振动以及“狮吼功”中的声音碎杯现象.

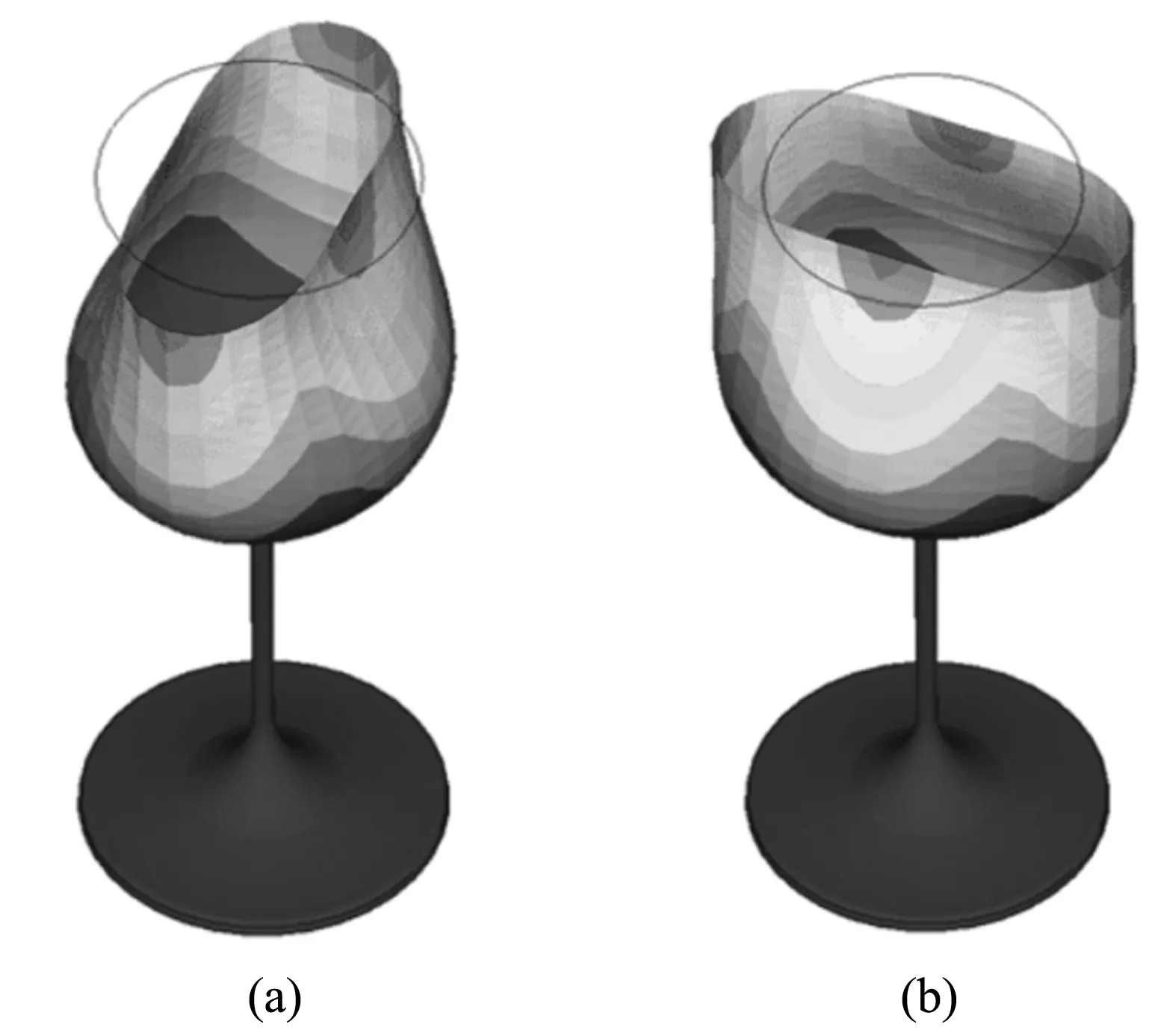
图片取自网页文献[2]，该网页上面可以看到杯子振动的动态模拟

3.1 桥梁的风致振动以及共振和颤振之辨

由钢筋混凝土建成的桥梁有弹性，因而在外力的作用之下也会发生振动，无论是塔科马大桥还是虎门大桥，在风致振动时都观察到了桥面的蛇形振动和周期性扭曲，感觉上是平吹过来的风，为何会产生周期性的力作用从而让桥梁振动起来？以虎门大桥2020年的振动事件为例，目前为止，有人认为是卡门涡街效应引起的振动(涡激共振) ，也有人认为是颤振. 所谓卡门涡街效应，指的是流体在流过障碍物之后会产生规律间隔的漩涡，如图2所示，这些规则漩涡会周期性地对桥面进行拱抬或压迫，如果漩涡的隆起周期和桥面的振动周期一致，那么前者就会不断地将能量传递给桥面，使得桥面的振动幅度越来越大，这就是涡激共振. 所谓颤振是一种自激振动，生活中常见的例子如：打开水龙头时，固定得不是很好的自来水管偶尔会产生伴随着哒哒声的较剧烈的振动——喘振现象，乘坐飞机时可以看到机翼片在空气中的振动，用较长的钢片的一部分去刮坚硬物体的表面(水泥墙棱或金属)的时候，整个钢片会振动起来等. 这些例子中，钢片的颤振比较容易理解，此时的外力是来自于金属或水泥墙的摩擦力，这摩擦力只有一个方向，也并没有周期性的变化，但是却能够让钢片剧烈地振动起来. 如果停止刮擦，钢片的颤振会因为阻尼的作用慢慢减缓并停止. 可见平动形式的刮擦做功是颤振能量的来源，在数学表示上，这种刮擦作用使得体系的总阻尼变成负值，阻尼既然为负值，那么振动的能量和振幅就会越来越大，最终产生破坏作用. 颤振过程能量传递的物理图像不好描述，但有一点是可以确定的，就是外力(不一定是周期变化的外力)和系统产生了某种耦合作用，将功源源不断地转化为系统的振动能，这一点是它和共振的共性. 经过上面的分析，还可以得出这么一个结论：无论是颤振还是共振，因较小的作用力造成较大的破坏作用，不但不违反能量守恒原理，反而恰恰是能量守恒的一个体现. 在整个振动事故中，外力做功源源不断地转化为振动能而没有得到及时的释放，振动振幅从肉眼看不见到逐渐增大再到剧烈振荡. 有文献指出，从计算结果和实验数据上看，造成塔科马大桥风毁事件和虎门大桥振动事件的主因应该是颤振，而卡门涡街效应只是诱因[1].

图2 卡门涡街效应[3]

3.2 “声音碎杯”的实现

用手挤捏杯口，发现并不需要用太大的力就可以将杯口捏扁约半毫米. 可见红酒杯的弹性系数并不是非常大. 普通人谈话传到1 m处时的声压为2×10-3～2×10-2Pa(参见百度百科“声压”条目).将靠近嘴边大喊的声压估为此值的50倍(10-1～1 Pa)并不为过 . 假设杯壁对声压的受力面积为10 cm2. 由此可以算得声压施加给杯壁的力作用为10-4～10-3N. 以上对红酒杯杯壁受力情况的分析数据表明，本文第2节中的计算基本可以适用于人对红酒杯嘶喊并产生共振时的情况(不至于带来非常离谱的误差). 从表1中我们可以看到，当杯子振动到2 500次的时候，杯壁的形变量达到1 cm，这个形变量足以让杯子破裂.

接下来的问题是人的嗓音能不能和玻璃杯产生共振？这要回到我们引言中所提到的《最强大脑》节目中吕飞龙的表演. 将该期节目有关“声音碎杯”部分的音频提取并转换为声波图像如图3(a)所示. 我们提取的音频一共1 min 29 s，其中有效的 “吼杯”时间是从50 s到55 s(图中两条竖线之间的部分)，值得注意的是，这段时间声音的强度其实并不是很大(甚至比该节目中其他时间的声音强度还小)，这印证了我们前面的说法：共振现象中，强度因素退居二线，频率因素才是主因. 我们将这段音频进行放大，得到图3(b). 由于振动太密，从图3(b)仍然看不清波形. 为此我们在这段音频上再截取两段(第2.8～3.0 s和第4.4～4.6 s)进行放大，分别得到图3(c)和图3(d).从图3(c)和图3(d)我们可以看到，吕飞龙对杯嘶吼时的声音频率非常稳定.在这两段音频中0.05 s内的振动次数都是28次，也就是说，频率都为560 Hz.该节目中南京大学赵其昌教授介绍说，经过他们的测试，该节目用的杯子的固有频率在500 Hz左右. 以上分析说明两点：(1)吕飞龙的嗓音可以达到节目所用杯子的固有频率.(2)吕飞龙的嗓音可以较长时间锁定在固定的频率. 同时，由碎杯所需的振动次数(2 500次)除以声波频率得到吼破玻璃杯所需的时间为4.5 s，与实际情况基本吻合.由此我们得出结论：徒口喊破红酒杯确有可能.

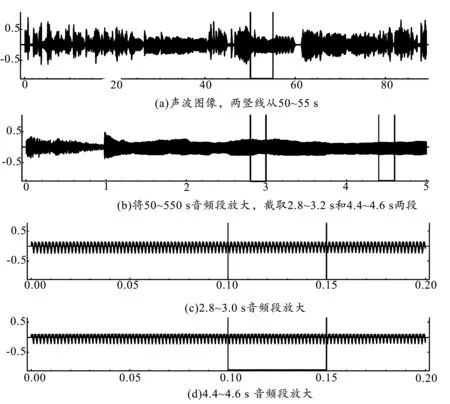
图3 吕飞龙嘶吼碎杯音频提取

事实上，据百度百科“声音”条目所载：在2005年的“探索”频道《MythBusters》电视节目上， 摇滚歌手兼歌唱教练杰米·温德拉就用自己的声音击碎了一些玻璃器皿，第一次证明了个人声音就能击碎玻璃的说法是正确的. 此外，在2012年的第6期《快乐大本营》节目上，歌手陈奕迅和主持人杜海涛均实现了用麦克风结合音箱喊破红酒杯，在2013年《快乐男声》6强赛节目上，歌手华晨宇用同样的方法3 s喊碎红酒杯，在掌握了大致要领以后，艺人于湉、欧豪、谢娜和维嘉都做到了30 s内借助音箱喊碎红酒杯. 2017年11月8日央视财经频道科教类节目《是真的吗？》节目上也播出了用音频发生器“响碎玻璃杯”的实验. 物理教师梁振华设计了简单可行的“声音碎杯”演示实验[4]. 而在吕飞龙的表演播出以后，国外一个网友在网络上发布视频称自己利用科学方法14天练成了徒口吼碎红酒杯的技能[5]. 由此可见，声音碎杯已属常见现象. 并且，就算不借助扩音设备，只要具备较高的音域和较好的锁频技巧，单纯用嗓音震碎玻璃杯的难度也并不是非常大，不需要练就绝世神功，也并无相关的“武功秘籍”.

从各种“声音碎杯”的表演中还可以总结出一套快速碎杯的方法：(1)轻敲玻璃杯，从它发出的响声大致判断它的固有频率(这样可以减少扫频的时间，以节省力气).(2)玻璃杯的振动情况肉眼不好判断，所以一般会在杯里面放一根轻质吸管. 杯子的振动会传递给吸管.(3)嘴巴张大靠近玻璃杯从第(1)步听到的频率附近开始嘶吼，嘶吼时一边慢慢变换频率一边观察吸管的振动情况，待吸管振动最猛烈时(共振开始)，锁住频率并加大音量直到杯子破裂.

4 结论

共振是当弹性系统受到与之固有频率相同的驱动力作用时发生剧烈振动的一种现象，属于受迫振动；颤振是弹性系统受到均匀外力的某种耦合作用时发生剧烈振动的一种现象，属于自激振动.它们的发生正是能量守恒原理的体现.两种振动的幅度和能量的积累都需要一定的时间，所以如能及早地改变外力与系统的耦合作用(例如通过改变系统的外形)，使外力做功不再继续转化为振动动能，那么，体系的振动就会因变成阻尼振动而逐渐衰减，以此减小共振或颤振带来的危害.比如这次的虎门大桥的振动事件中，专家组的初步判断就是：桥梁维护过程中“沿桥跨边护栏连续放置水马，改变了钢箱梁的气动外形……”，后经撤除水马，振动果然逐渐减弱，最后恢复正常通行. 而对于一般质地的红酒杯，只要音域稍高，锁频技巧较好的人都可以将其吼碎，并不是什么绝世神功，也并不像吕飞龙接受采访时所说“普通人轻易不要练狮吼功……跟天赋有关，也跟他练过武术有关”云云. 因为这门“绝技”所需的天赋，无非是稍高一点的音域，至于和练习武术之间，并没有多大的联系. 最后引用著名的物理学教育家沃尔特·略文(Walter Lewin)教授的名言作为本文的结束语：

“我就算不相信自己，也要相信物理学. ”