DELC深度学习模式的“九宫格”模型建构教学——以浙教版“电路的分析和运用”为例

木天乐

(温州市第二外国语学校 浙江 温州 325000)

在遇到有一定学习难度的内容时，选择合适的教学理论来设计课堂可以突破教学难点，帮助学生建构内在知识体系，促进深度发展.模型建构教学和深度学习理论为此提供了强有力的支持.

1 模型建构教学

模型建构是自然科学研究中的一种常用方法，通过研究模型来揭示原型的形态、特征和本质，能体现模型建构者较为高阶的逻辑思维能力和思维方式[1].因此，渗透该方法的教学是为了通过模型的建构，为知识迁移提供知识经验、认知结构和动作技能，促进高阶思维培养.

模型建构教学的过程为感知模型、建立模型、认知进阶和修正模型、应用模型.

2 深度学习及路线

深度学习，就是指在教师引领下，学生围绕着具有挑战性的学习主题，全身心积极参与、体验成功、获得发展的、有意义的学习过程.在这个过程中，学生掌握学科的核心知识，理解学习的过程，把握学科的本质及思想方法，形成积极的内在学习动机、高级的社会性情感、积极的态度、正确的价值观，成为既具独立性、批判性、创造性，又有合作精神、基础扎实的优秀的学习者[2].

美国的利恩·尼克尔森(Leann Nickelsen)和埃里克·延森(Eric Jensen)合著的《深度学习的7种有力策略》一书中总结出的深度学习路线(Deeper Learning Cycle，以下简称DELC)为设置课程目标和内容、预评估、营造积极的学习氛围、预备与激活先期知识、获取新知识、知识深度加工、评价学习者的学习.

可以发现，模型建构教学的过程和DELC中的学习过程有着非常紧密的联系，我们可以做一比较，具体如表1所示.

表1 DELC深度学习路线和模型建构教学的联系

而后，我们结合DELC深度学习路线和模型建构教学理论的优势，开展教学设计和教学实践.以“电路的分析和运用”一节为例，其教学设计框架如图1所示.

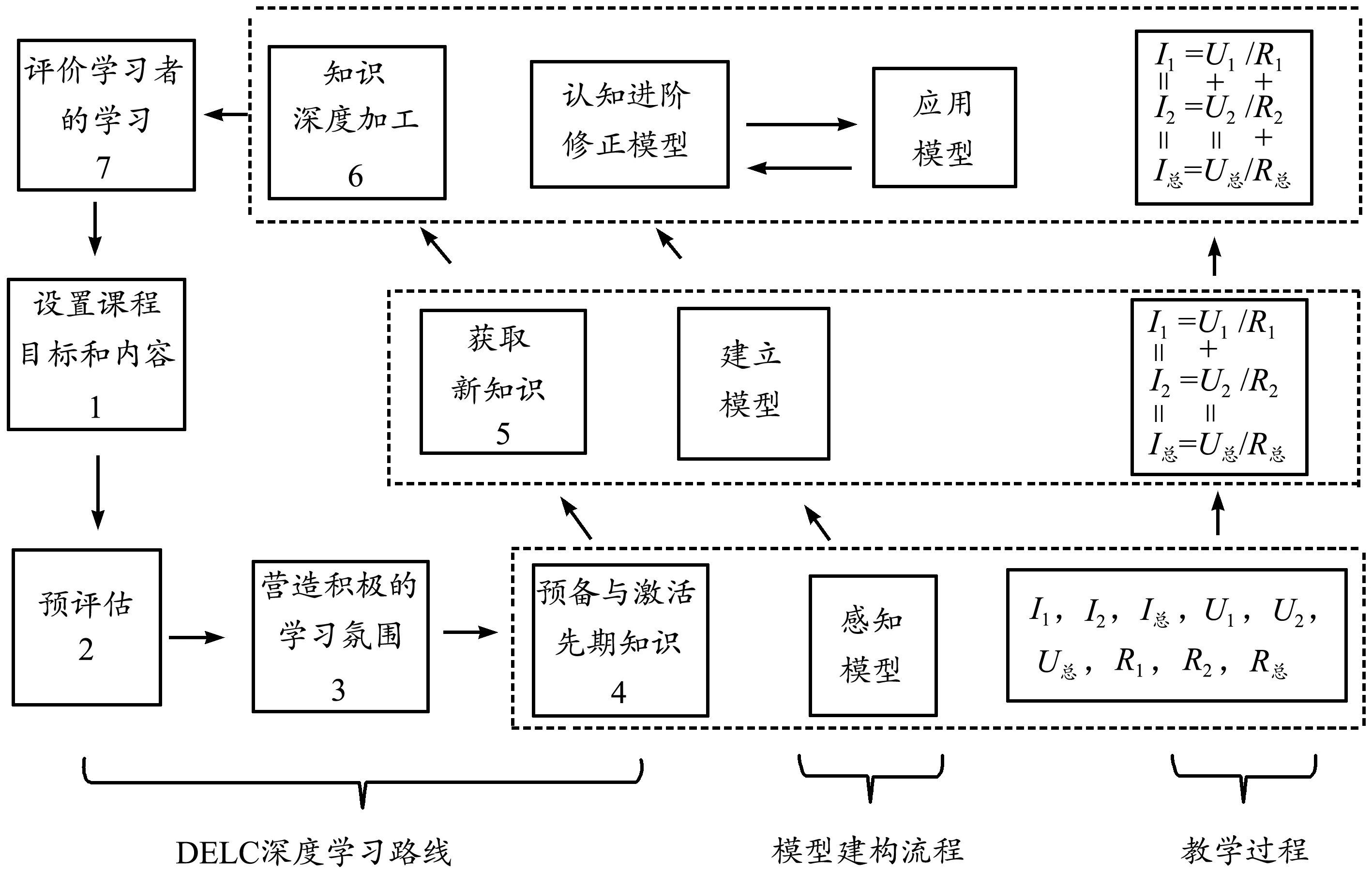
图1 “电路的分析和运用”教学设计框架

3 教学设计和教学实践

3.1 设置课程目标和内容

按照课程标准，本课需要达成的目标是“知道串、并联电路的电流电压特点，理解欧姆定律，并解决简单的电学问题.”[3]按照课本内容编排，该课的要点问题为串并联电路电阻特点、串联电路分压情况的计算、并联电路分流情况的计算.

3.2 预评估

浙教版八年级上册科学第四章“电路探秘”是初中生首次接触电学内容，这章前5节内容，让学生对电路、电流、电阻、电压等核心概念有了一定的认识，而后学生根据第6节电阻器电流、电阻和电压之间的关系，得出了欧姆定律.到了第7节“电路的分析和运用”，需要进一步研究多个电阻器之间的关系.本节的难点在于，一个电阻器存在3个电学物理量，而两个电阻器的电学物理量将多达9个，掌握难度成几何倍数增加.

3.3 营造积极的学习氛围

学习氛围是一种隐形的“场”，它取决师生之间的积极关系和学生之间的积极关系.对于前者，就要求我们教师在教学设计上以学生为中心，在课堂上，给与学生表达的时间，给与学生认可与尊重.对于后者，更多的是在长期课堂中，引导学生倾听彼此的想法，思考彼此的想法，认可或用证据否定彼此的想法，并认识到彼此之间的促进作用.

3.4 预备与激活先期知识：感知模型

(1)提供一个未知阻值的电阻器，设计实验测量其阻值.

(2)两个电阻器串联，指出涉及到的电学物理量.

说明：通过测单个电阻的实验，回顾了伏安法测电阻的实验和欧姆定律.在此基础上，引导学生思考两个电阻时电路中的相关物理量，为模型构建提供基础知识的支撑.

3.5 获取新知识：建立模型

(1)观察9个物理量，对其进行有序排列，并说明排序理由.

(2)若两个电阻并联，完成并联电路的“九宫格”模型.

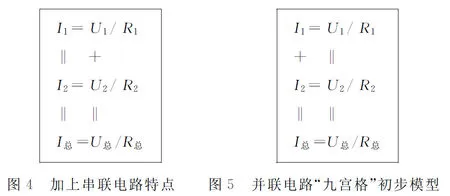
说明：学生介绍自己的排列方式和排列原因过程中，引导其他学生基于“欧姆定律”和“串联电路特点”进行生生互评，逐步构建串联电路的“九宫格”模型，如图2～图4所示，并将其拓展到并联电路，如图5所示.

3.6 知识的深度加工

3.6.1 认知进阶和修正模型

(1)通过现有模型，分析串联电路中R1，R2，R总之间的关系.

(2)若两个电阻并联，分析R1，R2，R总之间的关系.

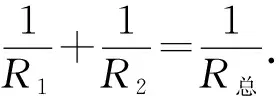
3.6.2 应用模型

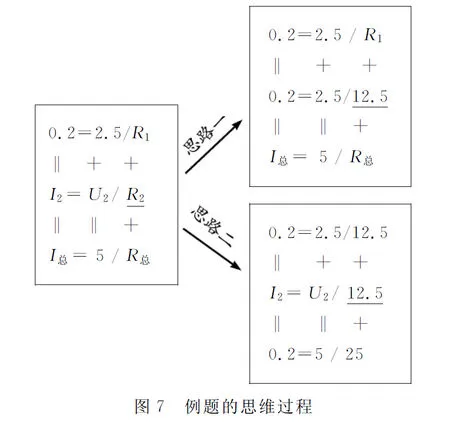
【例题】一个小灯泡正常发光时两端的电压是2.5 V，通过的电流为 0.2 A.现用一个电压为5 V的电源对其供电，为了使小灯泡能正常发光，需要串联一个多大的电阻？

说明：学生借助“九宫格”模型内物理量横向和纵向的关系，快速找出对应的关系和公式，得到结果，思维过程如图7所示.

3.6.3 认知进阶

(1)知3求6

1)利用例题中的3个已知数据，求出“九宫格”内尽可能多的物理量.

2)讨论“是否知道九宫格中任意3个数据，就能求出所有物理量”.

说明：在例题的基础上，所有物理量都可求出，数据如图8所示.随后讨论得出，“用3个不重复的物理量，可以求出其他6个物理量.”该过程借助模型深挖了物理量之间的联系，体现出该模型的优势.

(2)分压特点和分流特点

1)分析图8中U1和U2都为2.5 V的原因.

2)简单变式：一个小灯泡正常发光时两端的电压是2 V，通过的电流为0.2 A.现用一个电压为5 V的电源对其供电，为使小灯泡能正常发光，需要串联一个多大的电阻？

3)根据例题和简单变式的“九宫格”模型，推测U1和U2之间的关系.

4)结合“九宫格”，用公式推导出U1和U2之间的关系.

5)结合“九宫格”，用公式推导出并联情况下I1和I2之间的关系.

说明：完成简单变式的过程中，学生可求出所有物理量，结果如图9所示.结合图8和图9，让学生分析数据，发现分压特点U1∶U2=R1∶R2后，利用“九宫格”模型推导该规律，并引导学生推导出并联电路分流特点I1∶I2=R2∶R1的规律，推导过程如图10和图11所示.

3.7 评价学习者的学习

对学生进行的评价有形成性评价和终结性评价.形成性评价首先应该指向深度学习的目标，关注学生对学习内容的理解和迁移，而不能停留在简单的背诵、重复.其次应该具有情境性，基于学生的生活经验，从而更好激发学生内驱力，实现深度学习[4].终结性评价不是在一天的教学中所能做出的，应该在长时间的时间跨度下，教师、学生本人、同伴、家长共同评价所产生的.

故以教材课后练习第3题作为形成性评价的一部分，题目如下.

某同学在创作比赛中有这样一个设想，灯泡中采用两根灯丝，外接的电路中用两个开关控制电路，如图12所示.在外接电压220 V不变的情况下，灯泡中实际的电阻不同，通过灯泡的电流就不同，且电流越大，灯泡越亮.已知L1的电阻小于L2的电阻，问如何控制灯泡外的开关，使其产生3种不同的亮度？怎样控制灯泡最亮？

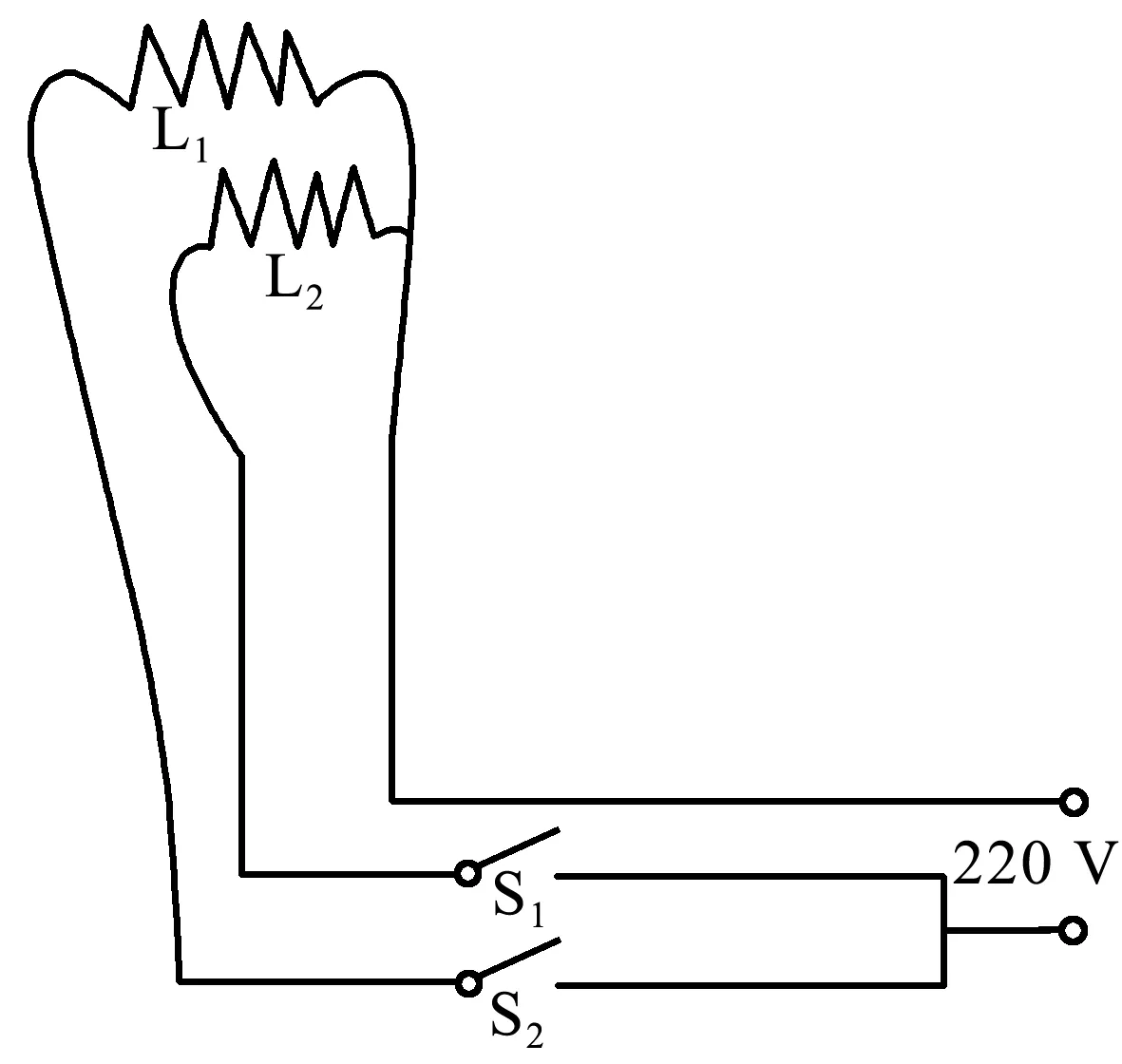
图12 某灯泡结构示意图