基于GeoGebra软件力的图示——以“四力平衡”为例

谢恩东 阮宜冬

(安庆市第一中学 安徽 安庆 246003)

用GeoGebra软件中的向量可以表示物理中的矢量，向量可以通过工具栏中的工具完成，也可以通过指令栏输入指令实现，无论是哪种方式矢量的获取都需要用到点，即起点和终点.物理学中最常见的矢量是力，用GeoGebra软件中的向量作出力的图示不仅精准而且还有动态变化的特点，在动态平衡问题中应用特别常见.在三力平衡类问题时，通常利用平行四边形法则，可以通过GeoGebra软件中平行线的方法来实现力的图示[1].四力或四力以上物体平衡时则要采用正交分解法，在GeoGebra中可以通过点的横、纵坐标来实现正交分解.

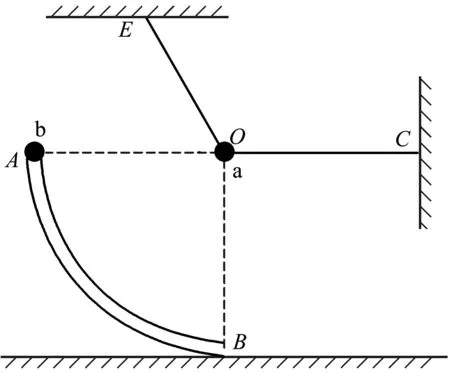
图1 例题图

A．小球b的机械能守恒

B．小球b受到的库仑力大小始终为3mg

C．悬线OE的拉力先增大后减小

D．悬线OC的拉力先增大后减小

答案：A，B，D.

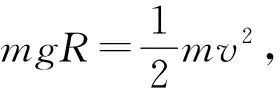
图2 正交分解法

三角形法：两细线拉力形成的原因是重力和库仑力，这两者是相互独立的，且重力是恒力，在分析细线拉力变化情况时，考虑重力与不考虑重力结论是一致.图3所示为不考虑重力情况下小球a的受力示意图，从力的三角形中可以看出悬线OC的拉力先增大后减小，OE的拉力一直增大.

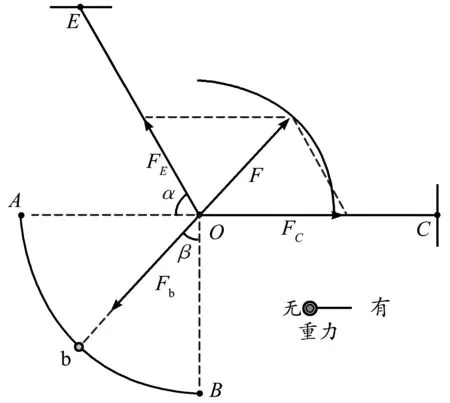
图3 三角形法

GeoGebra方法与技巧：

(1)如图4所示，按题图1在GeoGebra软件中作图，O为坐标原点，动点b表示物体b位置，滑动条只有“1”和“0”两个数值，分别表示考虑重力和不考虑重力两种情况，点F，G，H，I，J分别与力对应，其位置与物理意义如表1所示.

图4 GeoGebra中力的图示制作方法

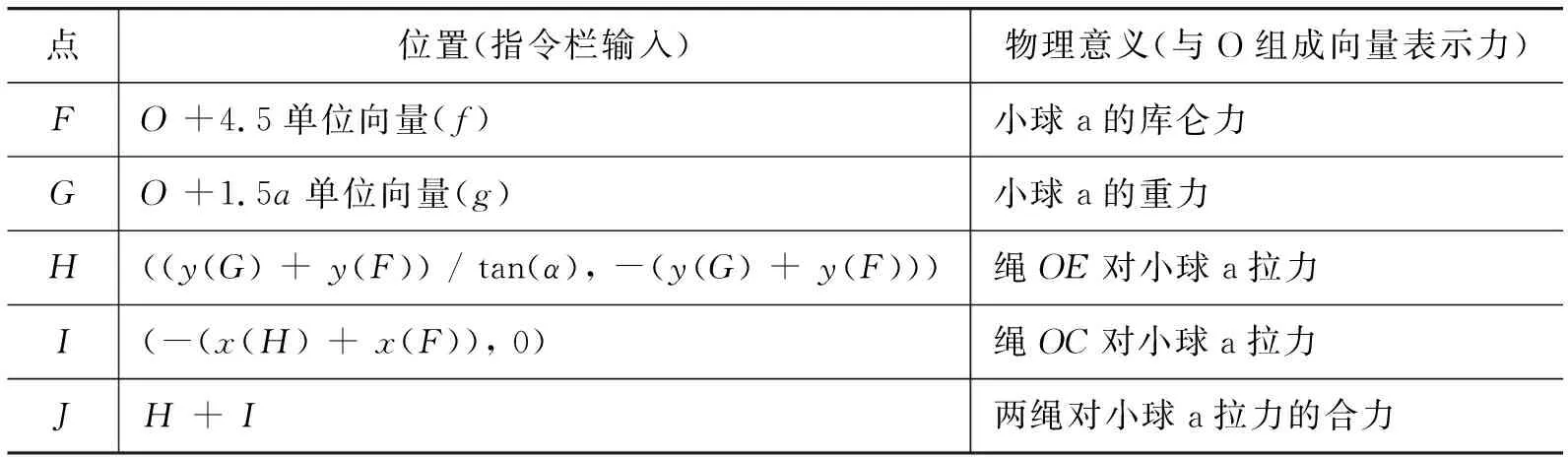
表1 各点的位置及对应的物理意义

(2)用“向量”工具将点连成向量表示相应的力，如，连O与H的向量表示库仑力，隐藏部分对象后效果如图2，3所示，图3中力F末端的圆弧为J点轨迹.

(3)设置部分对象的显示条件可方便课堂教学演示，如，表示两绳对小球a拉力的合力F的显示条件：滑动条a=0，可以实现合力F只在无重力情形显示，其他对象可参考同样方法.