以二次函数为载体的三角形面积最值问题的求解策略

河北省易县教育局教研室 段昆山 074200

纵观近年各地中考试卷，以二次函数为载体，结合几何图形求面积最值问题的题型是各地中考的高频考点之一.这类试题综合运用多种数学思想方法，不仅考查了二次函数与三角形面积的相关知识，又为后续学习高中知识奠定了基础.具有难度大、综合性强，区分度高的特点，很多考生感到束手无策.现以我县初三上学期期末考试试卷最后一题为例谈一谈以二次函数为载体的三角形面积最值问题的求解策略.

试题呈现：如图1，在平面直角坐标系中，抛物线y=ax2+bx+2（a≠0）与x轴交于A，B两点（点A在点B的左侧），与y轴交于点C，抛物线经过点D（-2，-3）和 点E（3，2），点P是第一象限抛物线上的一个动点.（1）求抛物线的 表 达 式；（2）当△BPC的面积取最大值时，求△BPC面积及点P的坐标.

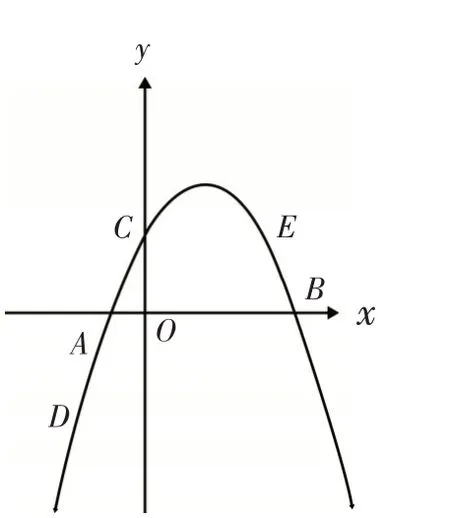
图1

下面重点分析第二问的解题思路.

1 求解策略一 分割法

1.1 提炼模型（如图2）

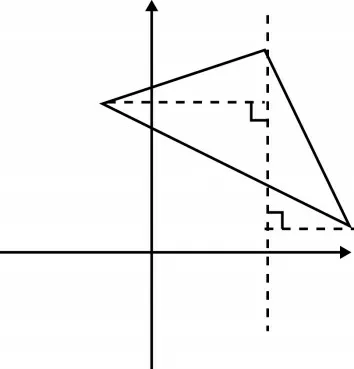
图2

1.2 模型解读

三角形面积通常用底乘高的一半面积公式来求，在平面直角坐标系中求斜三角形的面积直接用这个公式就求不出来了.那就得用转化的思想，把斜三角形分割成底与高分别与坐标轴平行的三角形，充分利用定点的横纵坐标来求三角形面积. 过点P作PE⊥x轴于点F,此模型△BPC就

1.3 试题简解

图3

2 求解策略二 补形法

2.1 提炼模型（如图4）

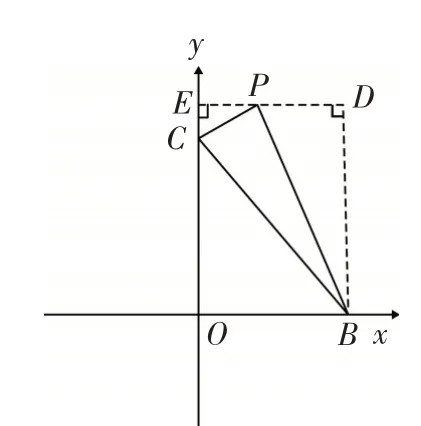
图4

2.2 模型解读

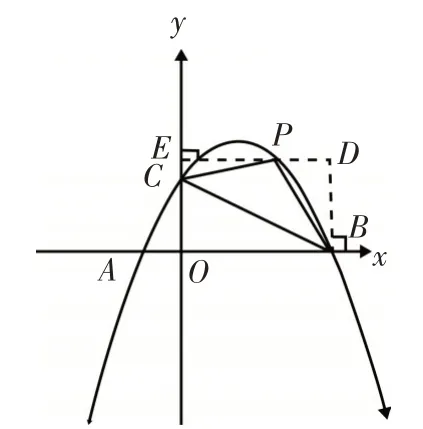
图5

除分割法外，求在平面直角坐标系中斜三角形的面积，也可以转换思路，用补形的方法把不规则图形转化成规则图形，把斜三角形面积转化成矩形面积减去三角形的面积.再充分利用定点的横纵坐标，就可以求斜三角形面积了.过点P,作DE⊥y轴，垂足为E.过点B,作BD⊥DE,垂足为D.则四边

3 求解策略三 铅锤法

3.1 提炼模型（如图6）

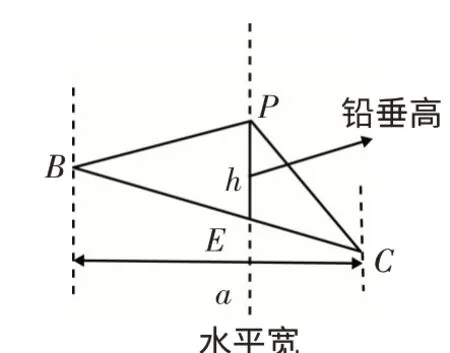
图6

3.2 模型解读

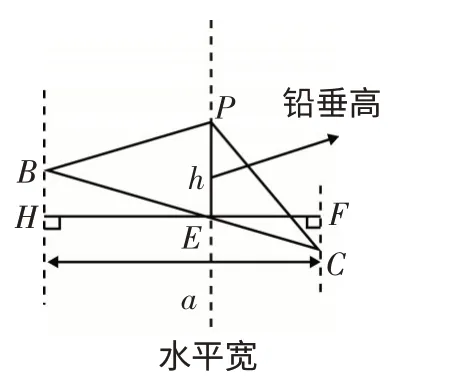
图7

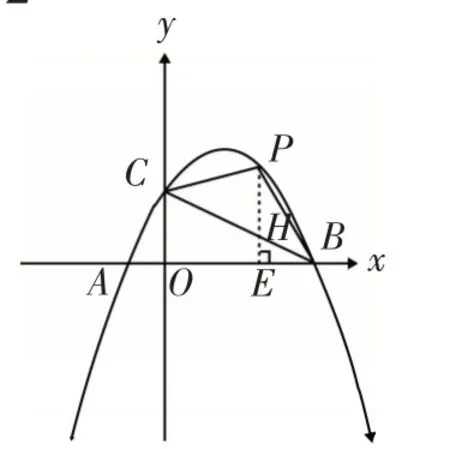
图8

4 求解策略四 平行线法

4.1 提炼模型

4.2 模型解读

如图9PH//BC，点H、P在直线PH上，点B、C在直线BC上.平行线间的距离相等，即△BPC和△BHC的高相等，底是BC. 所以△BPC和△BHC的面积相等. 求△BPC的面积就转化成求△BHC的面积.

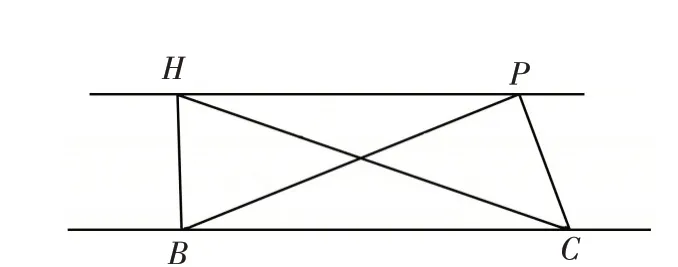
图9

4.3 试题简解

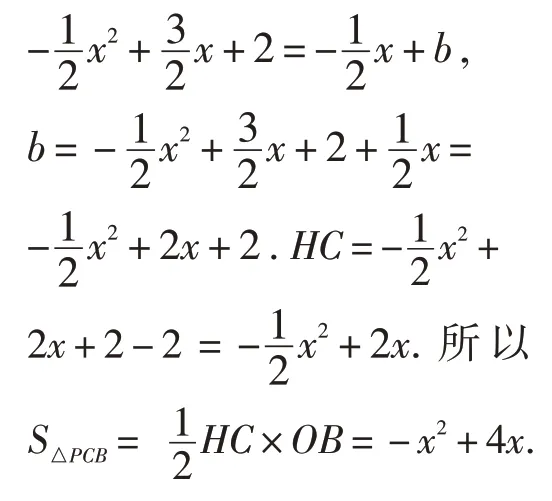
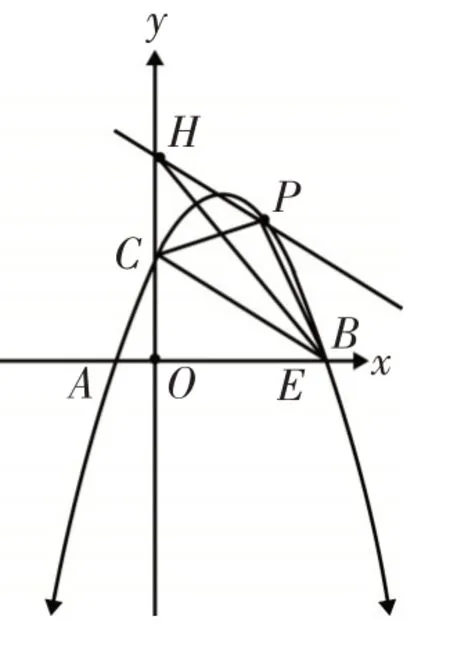
图10

5 求解策略五 相似法

5.1 提炼模型（如图11）

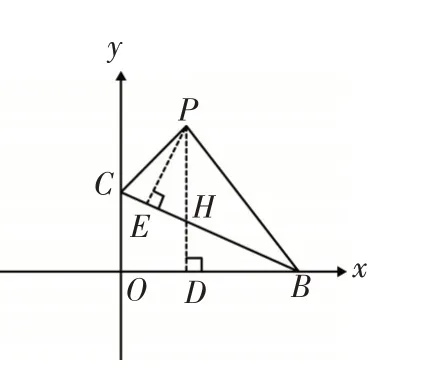
图11

5.2 模型解读

5.3 试题简解

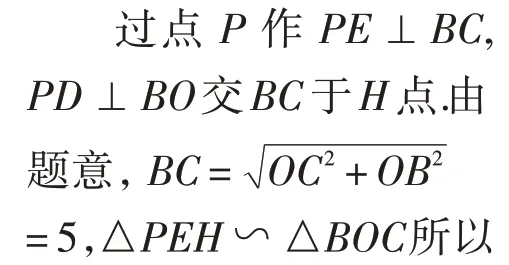
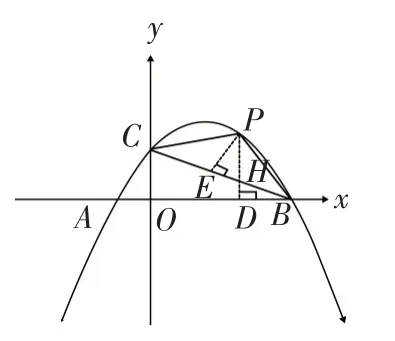
图12

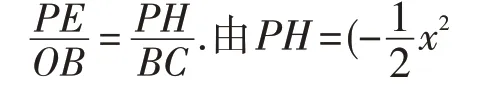
6 求解策略六——切线法

6.1 提炼模型（如图13）

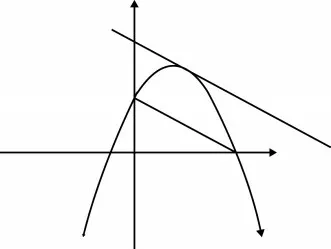
图13

6.2 模型解读

在图13 中，若P点在抛物线上使S△BPC最大. 则须使PE//BC且PE与抛物线有且只有一个交点，才能使S△BPC最大. 因为P点在抛物线上，PE与抛物线有且只有一个交点时，BC边上的高才最大.

6.3 试题简解

7 求解策略七 中点法

7.1 提炼模型（如图14）

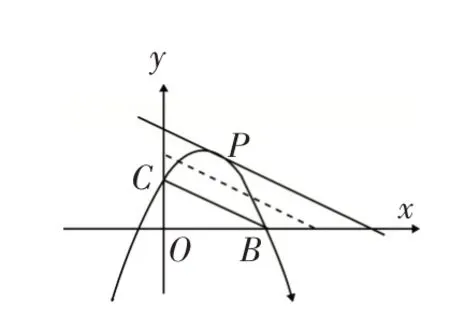
图14

7.2 模型解读

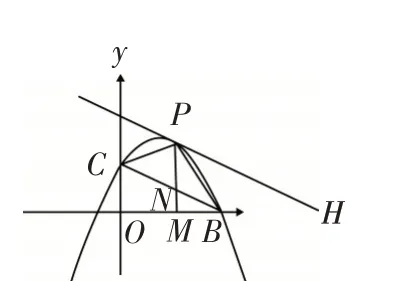
图15

感悟解法：这一类以二次函数为载体，结合几何图形求面积最值问题的题型涉及的知识面多、难度大、综合性强，要想顺利解答此类问题，必须抓住以下几点.首先，立足转化，抓住动点（设动为定）合理构造辅助线，以转化思想为基本出发点，抓住动点，根据不同思路过动点作平行或作垂直等辅助线，把复杂问题转化为简单问题,把未知问题转换为已知问题；其次，数形结合，设出动点坐标，充分挖掘已知条件与隐含条件，要明确角边在数量关系变化中哪些是保持不变的量，哪些是变化的量. 最后根据相关的数量关系，把面积表示成一个含有某未知量的二次函数关系式，然后利用公式法或配方法把最值求出来.