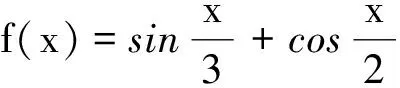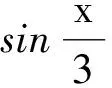一类三角函数的周期性问题探究

周思宇 (湖南省长沙市周南中学 410008)

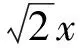
由于常值函数没有最小正周期，故本文所研究的函数都是定义在实数集上的连续非常值函数．

1 两周期函数之和的周期性

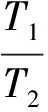
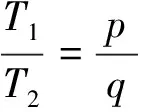
这里的T可以视为T1与T2的“公倍数”.公倍数与最小公倍数原是在自然数范围内考虑，这里借用这一名称是为了方便，现对其意义作一个说明：若干个实数的公倍数是指同时是其中每个数的整数倍的数，最小公倍数是公倍数中最小的一个正数.[2]

根据引理1我们可以知道，y=sinx+sin 2x是周期函数，2π是它的一个周期.

推论设f1(x)，f2(x)，…，fn(x)都是实数集M上的周期函数，T1，T2，…，Tn分别是它们的周期，若T1，T2，…，Tn中任意两个之比为有理数，则这n个函数的和(或差、积、商)也是M上的周期函数，周期是T1，T2，…，Tn的一个公倍数.

对于引理1与推论有三处需要说明：

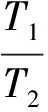
(2)引理1只是对两个函数的和(或差、积、商)的周期性提出了一个充分条件.也就是说两个非周期函数或者一个周期函数与一个非周期函数的和(或差、积、商)也有可能是周期函数．例如，f1(x)=sinx+x与f2(x)=sinx-x都不是周期函数，但f1(x)+f2(x)是周期函数．

(3)如果引理1中T1，T2都是最小正周期，则T=pT2=qT1不一定是f1(x)与f2(x)的和(或差、积、商)的最小正周期.例如f1(x)= sin2x与f2(x)=cos2x的最小正周期为π，但sin2x+cos2x=1，不存在最小正周期.

从上面可以看出，函数的周期性以及最小正周期是一个很复杂的问题．这里我们把研究范围缩小到三角多项式函数，并给出一个判断周期性的充要条件．

2 三角多项式的周期性

加强引理1的条件，可以得到如下几个判断函数周期性的充要条件.

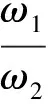
证明 (充分性)由引理易证．

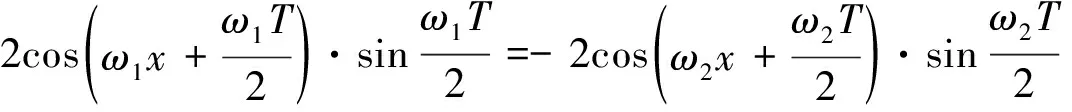
用类似方法可以得到sinω1x与cosω2x，cosω1x与cosω2x，tanω1x与tanω2x也具备类似定理1的结论.

定理1虽然给出了判断三角多项式是否具有周期性的一个充要条件，但是没有告诉我们它的最小正周期是多少.对于一般的周期函数，要具体找出最小正周期并无一般方法，但对于常见的三角多项式，可以找到一般方法．为了更好地得到这个方法，我们先给出一个引理.

引理2若f(x)是定义在实数集上的连续周期函数且f(x)不是常值函数，则f(x)必有最小正周期.

证明 假设f(x)没有最小正周期，则f(x)≡f(0)，证明如下：

因为f(x)连续，故对任意ε>0，存在δ>0，使得只要|x′|<δ，就有|f(x′)-f(0)|<ε.因为f(x)不存在最小正周期，故可以找到f(x)的一个周期T<δ，对任意实数x，存在整数n，使得x=nT+m，0≤m

定理2[4]设f1(x)=sinω1x，f2(x)= sinω2x(ω1>0，ω2>0且ω1≠ω2)，若ω1与ω2是有理数，则f1(x)与f2(x)的和(或差、积、商)的最小正周期是f1(x)与f2(x)最小正周期的最小公倍数.

证明 设F(x)=sinω1x+sinω2x，由定理1知，F(x)是周期函数.设T是F(x)的一个正周期，要得到F(x)的最小正周期，相当于求方程F(x+T)=F(x)的最小正值.

同理，sinω1x与cosω2x，cosω1x与 cosω2x，tanω1x与tanω2x也具备类似定理2的结论.

推论[4]设F(x)=(a1sinω1x+b1cosω1x)+(a2sinω2x+b2cosω2x)+…+(aksinωkx+bkcosωkx)，其中ωi是互不相同的正有理数，ai，bi(i=1,2,…,k)不同时为零，则F(x)的最小正周期为各项最小正周期的最小公倍数.

由此，我们可以得出y=sinx+sin 2x的最小正周期为2π.

函数的周期性是一个非常复杂的问题，本文旨在抛砖引玉，所研究的内容也仅仅是冰山一角.要想了解更多有关周期性的内容，还需读者继续涉猎相关知识.