2021年高考试题中的数学文化

范佳清 张维忠 (浙江师范大学教师教育学院 321004)

数学承载着思想和文化，是人类文明的重要组成部分．数学文化是指数学的思想、精神、语言、方法、观点，以及它们的形成和发展；还包括了数学在人类生活、科学技术、社会发展中作出的贡献和意义，以及与数学相关的人文活动．《普通高中数学课程标准(2017年版2020年修订)》强调高考试题要融入与渗透数学文化[1]．《中国高考评价体系》强调高考数学在考查过程中增加自然科学、人文与社会科学等多个领域以及现实生活、数学文化中的材料作为试题背景，考查学生运用数学知识解决实际问题的能力，促进学生数学素养的形成和发展[2]．为此，本文围绕2021年高考中的有关数学文化的试题进行分析讨论，以期为高考数学试题编拟和数学文化教学提供启示与借鉴．

1 试题特征

2021年全国各地共有10套高考数学试卷，包括全国甲卷、全国乙卷的文科卷和理科卷，新高考卷I，新高考卷II，北京卷，上海卷，浙江卷，天津卷．其中，有关数学文化的试题共有17题(文、理科卷中相同的试题视为一道)．

借鉴张维忠等的研究，按照内容类型将高考试题中的数学文化分为数学与人文艺术、数学与科技、数学与生活以及数学史[3]，将呈现形式分为附加型、可分离型、不可分离型[4]．

从表1可以看出：从内容类型上来说，数学与生活类的试题占了大多数，涉及扶贫、视力问题、生产等公共生活方面的内容，把社会问题融入到学生的学习生活中，引导学生关注民生问题，树立家国意识，彰显立德树人的教育之本．从呈现形式上来说，试题主要通过可分离型进行呈现，说明数学文化类试题仍需要注重与数学知识的关联，避免背景素材强硬地“附加”．

表1 2021年全国高考数学数学文化试题特征

2 试题欣赏与评析

2.1 以数学与人文艺术为背景

评析剪纸是中国最古老的民间艺术形式之一，能给人一种视觉上透空的感觉和艺术享受.剪纸作为一种原始艺术的载体，通过运用夸张变形的手法，将不同空间、时间的物像进行组合．此题以民间剪纸为背景，引入数列问题，为数列问题找到了真实的文化背景和现实意义，体现了数列知识与艺术的相关性及数学的应用价值．考生可以在感受中国传统文化艺术的基础上，抽象出其中的相关数列知识，发现对折后所得不同规格图形的种数呈等差数列，对折后单个规格图形的面积呈等比数列，很容易通过等差、等比数列相乘得到面积和．该题的重点在于对具体文化信息的理解和分析的能力，考查了考生的数学抽象素养．

2.2 以数学与科学技术为背景

例2(新高考卷II第21题)一种微生物群体可以经过自身繁殖不断生存下来，设一个这种微生物为第0代，经过一次繁殖后为第1代，再经过一次繁殖后为第2代……该微生物每代繁殖的个数是相互独立的且有相同的分布列．设X表示1个微生物个体繁殖下一代的个数．P(X=i)=pi(i=1,2,3)．

(1)已知p0=0.4，p1=0.3，p2=0.2，p3=0.1，求E(X)；

(2)设p表示该种微生物经过多代繁殖后临近灭绝的概率，p是关于x的方程p0+p1x+p2x2+p3x3=x的一个最小正实根，求证：当E(X)≤1时，p=1，E(X)>1时，p<1；

(3)根据你的理解说明(2)问结论的实际含义．

评析如今国内外的竞争越来越体现在科技的竞争，生物科学的发展也是科学技术中不可或缺的一部分．数学教育在科技创新和人才培养上的作用也不言而喻．该题以一种微生物的繁殖作为背景，展现了数学在生物科学中的重要地位，考生通过相应的概率求解公式即可解答，难度不大.该题考查了考生的问题理解和分析的能力以及数据分析能力．

2.3 以数学与生活为背景

图1

A.346 B.373 C.446 D.473

评析珠穆朗玛峰是世界上海拔最高的山峰，珠穆朗玛峰的高度一直是世界关注的问题．此题以珠穆朗玛峰的高度测量为背景，介绍了三角高程测量法，引入了立体几何问题，展现了数学与地理的紧密联系，体现了数学的应用价值和现实意义．考生可以根据题目中给出的三角高程测量法的示意图，借助线线关系、线面关系等立体几何知识构建计算模型，将题目的自然语言转换为符号语言．题目计算难度不大，重点在于考查考生的数学抽象、数学建模与空间想象能力．

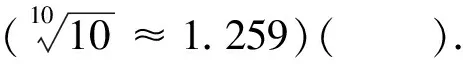
A．1.5 B．1.2 C．0.8 D．0.6

评析此题以社会广泛关注的热点问题作为背景，介绍了视力的五分记录法和小数记录法，展现了数学与社会发展的密切联系，体现了数学的应用价值与现实意义．该题考查了函数的相关知识，考生可根据题中给出的函数解析式，通过代入L值再进行化简后即可解答．该题考查的函数知识难度不大，但向考生传递了社会热点问题，体现了数学来源于生活又服务于生活．

2.4 以数学史为背景

例5(全国乙卷第9题)魏晋时期刘徽撰写的《海岛算经》是关于测量的数学著作，其中第一题是测量海岛的高．如图2，点E,H,G在水平线AC上，DE和FG是两个垂直于水平面而且等高的测量标杆的高度，称为“表高”，EG称为“表距”，GC和EH都称为“表目距”，GC与EH的差称为“表目距的差”，则海岛的高AB=( )．

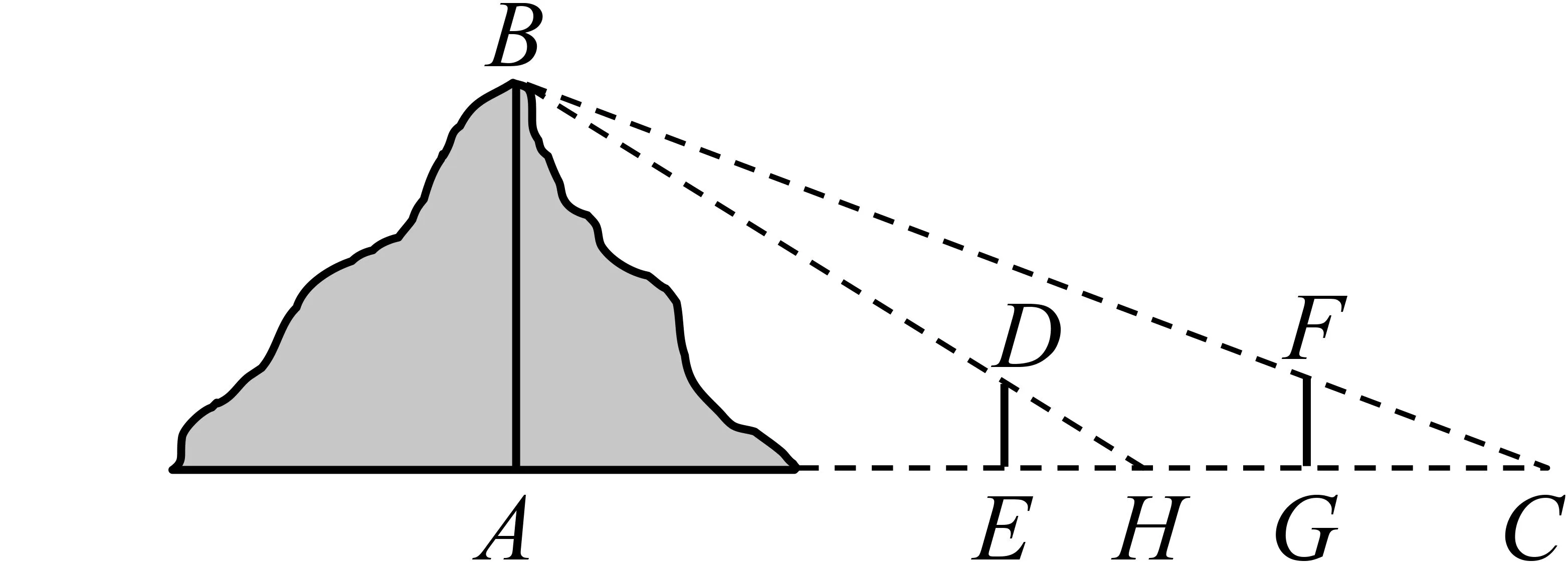
图2

评析《海岛算经》是中国学者编撰的最早的一部测量数学著作，为地图学提供了数学基础．该数学史背景强调了中国传统数学文化的价值和现实意义，让考生感受了中国古代数学测量的魅力．考生需要正确理解题干中的“表高”“表距”“表目距”等信息，结合几何图形解答.该题主要考查了学生对信息的理解和分析的能力、数学建模能力及数学抽象能力．

3 对命题的建议

3.1 巧妙融入人文艺术与数学史，传递文化价值，彰显数学魅力

数学史具备实用性，能够展示数学发展的历程，也包含美学标准、智力好奇、趣味娱乐等等，可以让师生感受到数学文化的多元性[5]；而人文艺术与数学的融合能充分展现数学的审美价值．根据统计结果可以发现，试题类型中含有人文艺术和数学史的较少；为了充分利用数学史、人文艺术的文化价值，命题者可将它们用历史资料或者图片的形式灵活地呈现出来，通过结合并借助数学文化中的人文精神来训练学生的思维，提高信息的理解和分析的能力．

3.2 采用合适的呈现形式，展现数学应用价值

数学文化情境的呈现形式对于考查学生的核心素养有重要作用.2021年全国高考数学文化类试题的呈现形式主要以可分离型为主，命题者需要增加高考数学试题与实际生活、社会生产的联系，适当地采用不可分离型的试题，让学生通过文化理解数学或者用数学解决文化中固有的问题，展现数学文化的应用价值、科学价值、人文价值和美学价值．

3.3 设计多样化题型，拓宽数学文化的渗透路径

当前数学文化题型多以选择题和填空题为主，题型较为单一．命题者可以结合学生的实际和考试的效度选择丰富的数学文化素材，设计相应的选择填空题和解答题；解答题的题干较长、隐含信息较多，比较注重数学思想方法的灵活运用，与题干简洁的选择填空题相结合，信息提取难易均衡分布，数学文化渗透自然．