融合数学思想 促进解题教学——“用对称性解决反比例函数问题”专题教学

朱 琛 (江苏省无锡市第一女子中学 214002)

1 学情分析

无锡市第一女子中学是无锡唯一一所只招收女生的特色学校．本课教学对象正是初中部的女生．进入初中后，女生对数学学习都有畏惧心理，她们的数学思维能力比较弱，解决问题时的反应较慢，因胆小怕出错，数学课堂的学习参与热情也不高．目前，学生的问题不仅存在于思维方面，运算方面也较薄弱．

2 教学内容解读

函数是数学研究中的一个基本对象，也是数学课程中最为重要的学习内容．初中阶段函数学习的好坏程度，直接影响着学生学习数学的积极性和信心，对后续学习的影响非常大．

初中阶段一共学习三种函数：一次函数、反比例函数、二次函数．苏科版将前两个函数分别安排在八年级上、下两册．苏科版八年级下册的反比例函数不同于八年级上册学习的整式形式的一次函数，反比例函数的解析式是分式形式的，分式的计算相对于之前所学的整式的计算稍复杂些，而且反比例函数的图象是双曲线，相对于一次函数图象是直线又变复杂了，知识呈现螺旋上升的状态．

可能受知识系统的局限(涉及一元二次方程的求解是苏科版九年级上册的学习内容)，苏科版《反比例函数》这章只介绍了双曲线的中心对称性，没有将双曲线的轴对称性纳入其中．就目前所学能说明其对称性存在原理，能完整呈现反比例函数及其图象的对称性，并且还能充分挖掘出蕴含的数学思想，让学生对此进行探究，还是值得的．

3 教学前诊断分析

3.1 学生认知

前期学习了一次函数和反比例函数的概念，也进一步认识了反比例函数解析式中|k|的几何意义，学习了因式分解和分式的计算，对数形结合和对称性(局限于几何对称)有一定的理解，这些为本课的研究奠定了良好的基础．但因反比例函数图象是双曲线，从直线到曲线的螺旋上升易让学生出现求解困惑：图象变得复杂，学生不知如何入手考虑；学生不会求解曲线和直线的交点．

3.2 与本课目标的差距

对数形结合思想和对称思想的感悟，需要学生具备敏锐的观察力、准确的语言表达、灵活的思维能力和综合应用能力．敢于大胆猜想，进而实施推理论证，这些都是女生所缺乏的，需要重点培养和改进．

3.3 应对策略

在进行“反比例函数的图象与性质”第1课时教学时，通过画图和操作，学生都能观察出这两种对称性，教师及时对她们的发现进行肯定和表扬．将对称性问题作为专题研究，既实现乘胜追击，完整呈现双曲线的对称性，又能在学生具备一定解决反比例函数问题的能力后，挑战较难的问题，给予她们更多的解题策略和成就感．

教学目标 (1)观看数学史中利用对称发现或解决问题的事例，感受用对称性解决问题的简捷性和有效性；(2)学会利用对称解决有关反比例函数问题；(3)逐步形成良好的数学观察能力，猜想、探究以及归纳问题的能力．

教学重点 进一步理解反比例函数的代数特征和几何特征．

教学难点 反比例函数对称性的证明及运用对称性解决有关反比例函数问题．

4 过程实录

4.1 情境创设

观看一段小视频(形如y=kx+b的直线能画出玫瑰线、雅各布线、笛卡尔线、阿基米德线、心脏线等这些美图)，再展示初二上学期勾股定理论证中刘徽的“出入相补”原理的证法图和杨辉三角．

设计意图用灵动而美妙的音乐，配合直线运动产生各种对称图形的视频，消除学生上公开课的紧张情绪，使她们的思维活跃起来，同时将学生的关注点引入到本课的课题上来．展示两位数学家用数形结合思想和对称思想发现规律并解决问题，引导学生从对“数学美”的欣赏，转化到用“数学对称”来考虑解决问题．

4.2 回顾与思考

师：反比例函数的关系式是什么？

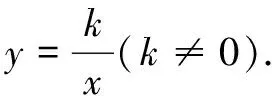
板书：代数特征：xy=k(k≠0)．

师：反比例函数的图象有什么对称性？

生(齐)：中心对称和轴对称．

板书：几何特征：中心对称和轴对称．

4.3 师生共同探究

4.3.1反比例函数图象中心对称性的探究

师：上面两种对称是通过画图、操作发现的，并未进行理论论证，所以请大家思考第一个问题：如何论证反比例函数图象是中心对称的？

(学生沉默思考……)

师：是否存在困难？

生：有困难．

师：如图1，对于图象上任意一点A．

图1

生1：先考虑点A关于原点的对称点，再考虑此点是否在这条双曲线的另一支上．

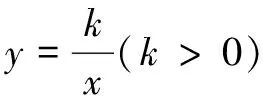
设计意图解决曲线中的全等是学生暂时没有接触的一块领域，所以出现困难是正常的.教师适度提醒，学生寻思对策，让学生运用转化思想将曲线问题转化成点的问题来考虑，使学生获得了一种解决问题的策略．

4.3.2反比例函数图象的中心对称性应用

生2：(板演)如图2，构造了两个矩形，得到矩形的面积都等于6，原式=(x1-x2)(y1-y2)=DF·CE=2OC·2OD=4OC·OD=4×6=24．

图2 图3

点评学生运用了数形结合思想，画出图象后，将点坐标的差转化为线段长，同时还运用中心对称性，结合图形的面积来求解．这充分展现出学生对以上思想和方法有了良好的认识和运用能力．

生3：如图3，利用中心对称，得点B(-x1, -y1)，原式=2x1·2y1=4x1y1=4×6=24．

点评用数形结合画出图象，根据中心对称可得点坐标的特殊关系，进而再利用代数特征求值．这同样展现出学生将数形结合和对称性两种方法融合起来解决问题．将图3归纳为模型1，方便学生直观理解和记忆．

设计意图类型1让学生感受“数缺形时少直观”，所以要画图，特别今后遇到更为复杂的问题，图象能直观呈现内在关联．通过这种方式操练，使学生自觉形成数形结合解决问题的常规方式：先画图，再观察研究，有利于学生后续独立学习习惯的养成．对称性在这里起到关键性的作用，将问题解决变得更为简单．

4.3.3反比例函数图象轴对称性的探究

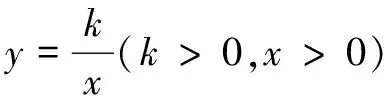
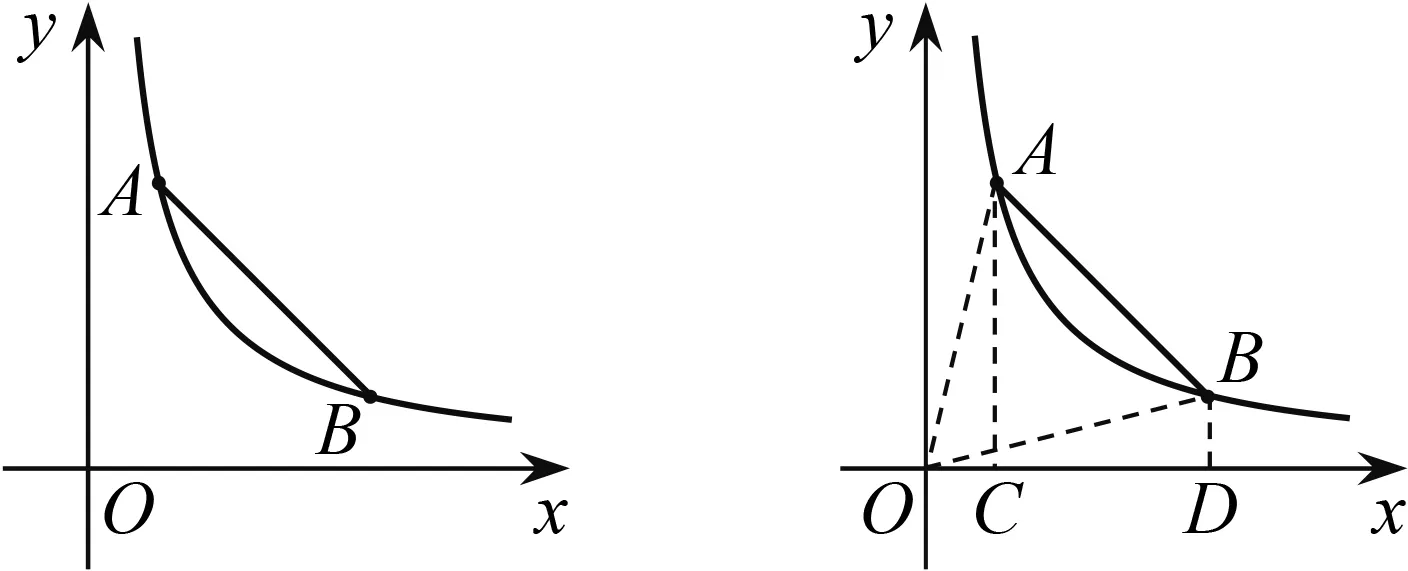
图4 图5

师：看到以上问题，能否猜想出结果？

生4：(4,1)．

师：你是如何发现这个答案的呢？

生4：根据轴对称性，对称轴是直线y=x．

师：能否具体说说？

生4：如图5，根据图形，可以发现△OAC≌△BOD，由此可得点B的坐标．

师：那么这两个三角形又该如何证明全等呢？

此时学生答不上来了．

点评虽然这位学生没有完美解答出来，但是她能够感受到图形的对称带来的“相等”，同时也找到了求点坐标的方法，即通过三角形全等．

笔者将学生4给出的图形稍作修改(过点A，B分别向y轴、x轴作垂线，垂足为C，D，如图6所示)让学生再来感受轴对称性以及全等，学生就能发现论证方法了(证略)．

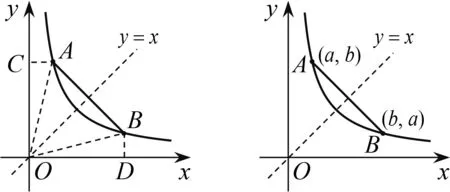
图6 图7

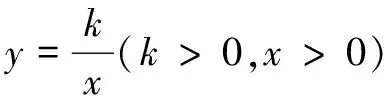
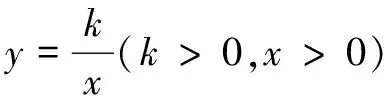
利用以上规律，设点A为任意一点，即可总结出双曲线的轴对性这一特征．我们将如图7的轴对称模型称作模型2．(让学生观察模型2，并阐述模型所包含的3个特征：①两点A,B都在双曲线的一支上；②AB所在直线与直线y=x垂直；③点A,B的横、纵坐标轮换.)

设计意图探究双曲线的轴对称性与中心对称性的探究类似，由于涉及的细节多一些，所以将问题设计成由特殊到一般的方式来解决，降低了学生理解和计算上的困难．在讲解中，教师将一次函数x+y=m和反比例函数xy=k的两个代数特征结合，引导学生发现代数式中也存在对称．借助反比例函数图象，将数的对称(代数对称式)和形的对称(几何对称)融合在一起，再次展现出数形结合和对称性融合的魅力，这就是本课研究的精华所在．

4.3.4反比例函数图象轴对称性的应用

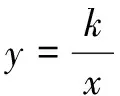
图8

A．-1 B．1

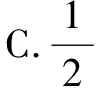
生5：通过观察，符合轴对称模型，所以考虑作对称轴直线y=x，即点F,E关于直线y=x对称．

师：除发现点F,E轴对称外，联系条件AB，你又能发现什么？

生5：△AOB是等腰直角三角形，所以直线y=x也是它的对称轴．

师：如果直线y=x与直线AB的交点为M，你能得到哪些点的坐标？

根据以上提示，学生依据中点坐标公式，依次求出点M,E的坐标，最后得出结果．

设计意图此题考查学生对模型的理解记忆能力．学会从图形整体观察对称，从而找出中点，利用中点坐标公式快速得出结果．解决轴对称问题，其核心就是找到对称轴，学生在运用时，需注意对模型3个特征的整体把握．

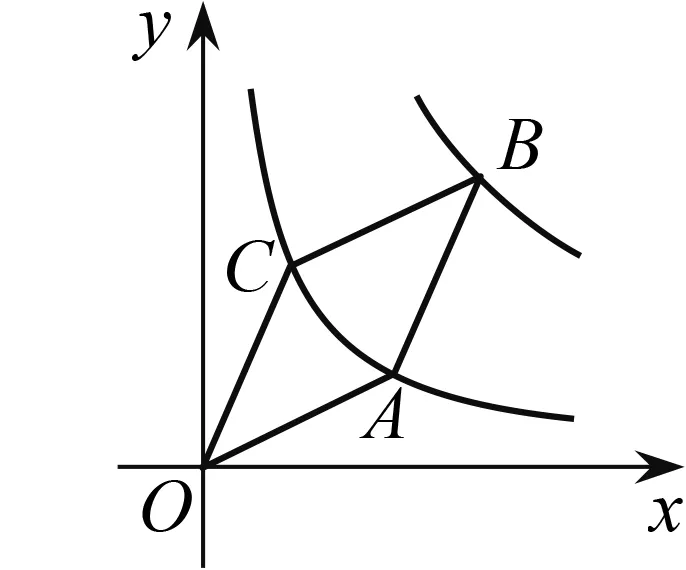
图9

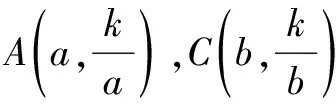
设计意图万变不离其宗．将两条反比例函数图象与菱形结合起来考查，提升学生识别对称性的能力，除学会直观感受(猜想)外，还要透过现象看本质(符合模型2的部分特点)，进而促使学生深入探究(验证)，用所学知识(解含字母的方程)来求A,B坐标，并总结归纳出模型3(图10)．

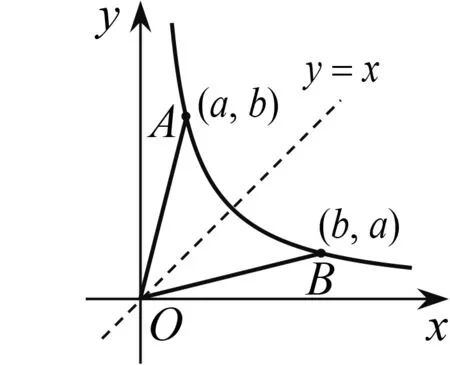
图10

4.4 课堂小结

对于反比例函数及其图象，我们应该关注其代数特性和几何特性，它们都具有对称性，学会了利用对称性解决问题，求解也就变得相当简便．

5 教学感悟

(1)以课本为主，但不依附于课本编写教案

教科书是学生获取系统知识的重要工具，也是教师进行教学的主要依据．《义务教育数学课程标准(2011年版)》提出加强基础知识和基本技能的训练，使学生对客观世界的各个方面、对物质运动的各种形式有一个基本又相对完整的认识．教师可以在数学教学活动时，创造性地使用教材，为学生提供丰富多彩的学习资源．在课本“反比例函数图象与性质”中提出中心对称的基础上，增加反比例函数图象的轴对称性，符合科学知识的系统性和学生的可接受性，将两者有机地结合起来，以学生可以接受的形式反映出来，才能使学生从客观事物的发生、发展中去认识其本质．

(2)以学生认知为主，深度学习，探究数学思想方法

通过描点法画出反比例函数图象后，学生普遍能发现双曲线的中心对称和轴对称这两种对称，而验证方式却只能停留在折一折、转一转的操作方式上．因反比例函数在历届无锡市数学中考中出现机会不多，有些教师就觉得这部分内容没那么重要，就会以灌输式、填鸭式的方式要求学生记住这两个性质便可，不再进行理论论证(确实耗时，需要增加课时及配套练习，而且没有现成资料)．这种浅层学习，太急功近利，不利于学生的思维发展．数学知识及规律的产生，都是需要靠操作和理论相结合才能获得的．只要让学生在已有认知的基础上，通过教师的适当引导，获取解题的经验，无关成败，这才是经验中“经”的意义所在．通过论证，进一步发现反比例函数图象的对称性是由个体(曲线上的任意点)的特征获得整体(双曲线)的特征；与一次函数y=-x+m图象结合，将代数对称和几何对称之间“数”与“形”的完美转化体现得淋漓尽致．通过深度学习，学生才能将已有的概念和经验联系起来，上升到数学思想的层面，用数学的思维思考问题、分析问题、解决问题．

(3)以解题为主，学习解题，增强解题信心

函数类解题通常由线与线的交点坐标来突破．因为学生认知的局限(一元二次方程的求解暂时没有学习)，所以没有进行代数与几何的对比解题，这是本课的一个遗憾．正因为受代数解法的局限，单从几何直观发现对称性来解决，结果使问题解决简洁明了．教师设置同类型问题，引导学生探究后作出归纳，用几何模型形式呈现，使学生能从较为复杂的图形中快速辨别符合条件的特性，以此让学生感受对称性所带来的解题快感．几何模型运用在解题教学中，将各种信息融合在简易图形中，化繁为简，化难为易，直观性强，便于学生记忆理解，是几何解题中常用的一种解题策略，深受学生的喜欢．对于数学解题，女生通常畏惧，无论是作业练习，还是考试测验，通常留空很多．学习解题，教师要有良好的示范，要向学生呈现正确的数学方法及数学思想，特别是图形问题，要带动学生在图上边标记、边思考，分清哪些是已知，哪些是未知，思考有什么方法能将这些条件或结论联系起来……学习了对称性后，观察(或构造)全等，描出对称中心或画出对称轴都是首先要考虑的，尝试着画一画、看一看、量一量，大胆猜想，验证猜想，潜移默化地将这些做法变成数学解题的习惯．理解数学、学习解题的过程就是“直觉—试探—出错—反思—猜想—证明—反思”的过程，将少量正确转变成大量正确，甚至完全正确，让学生对数学解题由最初的无信心转变成有信心．