互联网环境下优化高中数学课堂教学的探索*

陈广山 (江苏省苏州市第四中学 215003)

近些年来，我国教育信息化2.0行动计划与“互联网+教育”等工作协同扎实推进，给课堂教学带来了新的机遇和挑战．《普通高中数学课程标准(2017年版)》指出，教师“要注重信息技术与数学课程的深度融合”，刘喆、李利等人也分别在研究部分案例后指出，智慧教室使用上存在资源库使用较少、信息加工和知识建构的工具价值未能凸显、即时的资源没有得到有效应用等问题[1][2]．如何把互联网和通信技术、大数据、电子交互式白板等新技术新媒体与传统课堂融合，从而提高课堂教学效率，促进学生深度思考？本文以让技术服务教育为原则，以实现常态化应用为出发点，结合教学案例，谈谈利用互联网环境构建高效课堂的探索与实践，以期抛砖引玉．

1 从静态课堂转向动态课堂，互联网成为探究工具

我们知道，教师按照预设的PPT一页一页往下讲，讲得越多，课堂越沉闷，而学生被动地等待教师给出现成问题，练得越多，就越来越不会发现、提出问题和解决真正的问题．基于学生核心素养的教学要特别重视情境的创设和问题的提出[3]．互联网生态下，能否在数学活动过程中为学生创设身临其境的真实情境，激起学生探究的欲望，甚至让学生自己提出问题？

案例1换底公式的引入和探究．

问题1ln 1,ln e的值是多少？那么ln 2的值是多少？

生1：根据对数的意义，ln 2的值介于0和1之间，除非按计算器．

活动1 学生借助平板电脑用几何画板中的计算器得出其近似值．

问题2你还能按出哪些对数式的值？

生2：自然对数和常用对数都可以直接按．咦，log23怎么按呢？

师：有这回事？大家试试看．

活动2 操作探索，小组交流，学生讨论后觉得可能几何画板中的计算器功能不全，转而找其他计算器，发现电脑附件中自带的计算器仍然按不出，有的学生通过网络搜索其他计算器，有的开始陷入思考．

生2：我觉得计算器设计者不会那么“笨”，是不是有某种方法可以实现？比如说转化为常用对数或自然对数．

生3：老师，我在百度搜索到的一款科学计算器也是不能直接按log23，说明中说要转化为常用对数或自然对数．

问题3请同学们思考，如何由ln 2,ln 3的值求log23的值，你能得到一般的结论吗？

活动3 借助计算器计算分析，先猜想计算公式，再证明公式；借助对数的定义，直接分析求解．

这里没有直接让学生思考问题3，而是创设问题探究的真实情境，在情境活动中让学生发现问题，借助推理明确研究对象(换底公式必然存在)，把网络搜索作为探究活动走向深入的催化剂，情境和问题轮流驱动，促使问题探究走向深入．探究中，学生成为活动的主体，把“互联网+”信息技术作为实践探索的工具，在矛盾冲突中不断提出问题、分析问题、解决问题，并通过探寻数据间的内在联系，积累活动经验，促进学生创新能力的发展．

2 从知识课堂转向文化课堂，互联网成为资源平台

爱因斯坦曾说：“所谓教育，是学校知识全部忘光后仍能留下来的那部分东西．”诚然，知识和技能是数学教学的基本要求，而完美的数学教育更应追求数学文化的教育，即“数学的思想、精神、方法、观点、语言及其形成和发展过程”的教育[4]．

案例2一道复数题的“究”错．

已知复数z=cos 140°+i sin 140°，i为虚数单位，则下列说法中正确的是( )．

A．z的虚部为i sin 140°

B．z在复平面上对应的点位于第二象限

本题主要考查复数中的基本知识和运算，属于基础题，但是漏选D的学生不少．从应试角度，讲评时可以用“代入z3计算即得D是正确的”一句带过．然而，强调以知识和技能为载体，重视培养学生能力的教师不会浪费这样的机会：

师：z2=(cos 140°+i sin 140°)2=cos 280°+ i sin 280°，z3=z2·z=(cos 280°+i sin 280°)(cos 140°+ i sin 140°)=cos 420°+i sin 420°．请计算z4，能否有更一般的结论？

生1：若z=cosθ+i sinθ，则zn=cosnθ+

i sinnθ．

而具备数学文化意识和互联网思维的教师，会抓住时机再提出如下问题：

师：(在数据平台中点出一个漏选D的学生)你为什么没有选D？

生2：我没有计算，就感觉140°的角不可能算出特殊值来．太意外了，压根没想到有这么奇异的运算！

师：感觉可以有，但有时会被带歪，还是要小心求证．你觉得特殊在哪里？

生2：复数的n次幂，就是把角变成原来的n倍．

师：复数在形式cosx+i sinx下乘方引发了优美的结果，如果有时间，大家还想研究什么？

生3：会不会在其他运算中也有？

生4：复数的表示形式一变，竟有这么大威力，有没有什么其他应用？

师：这种形式叫复数的三角形式，相关的欧拉公式eix=cosx+i sinx在高等数学里占有重要地位．(教师同时推送复数乘除法运算的三角表示、1的n次方根、“一个上帝创造的公式”eiπ+1=0等阅读资料)

最后几分钟的课堂教学，教师引导学生跳出复数幂的运算，进行发散性的思考，把一道平常的纠错题上成了究其来龙去脉、究其文化内涵的题．利用互联网资源发现学生2仅凭感觉而错过了数学中美丽的风景，复数三角形式几种运算结果都那么简洁，从而引导学生养成良好思维习惯，培养了严谨和崇尚理性的精神；利用互联网了解了在复数域中，看似不相关的指数函数和三角函数竟然能联系在一起，感受了数学知识内部的和谐也感受到数学语言的魅力；利用互联网资源了解了公式“eiπ+1=0”竟然把数学中五个最有特色的数联系在一起，从而欣赏到数学的奇异美，感受到数学的魅力．虽然学生不能完全明白其中的原理，但这种文化价值的浸润和良好的情感体验不是单纯解题所能体会的．课堂几分钟的拓展阅读可能会带来了的是学生课后数个小时的专研，也可能正好拨动了学生心中的某根弦，让他爱上数学．数学教师的梦想应该包含让学生打心底里欣赏数学的美，喜欢数学的精神．通过互联网，我们看世界可以更加清晰和全面；通过互联网，我们可以丰富教学内容、传递文化．

3 从独白课堂转向对话课堂，互联网成为互动平台

对话课堂强调在师生平等的基础上，唤醒学生的批判意识，和衷共济，双向多边交流，提升课堂活力[5]．在“互联网+”的教学生态下，学生可以获得丰富的教学资源，技术平台已经可以便捷地支持课堂上的互动展示，比如学生可以在平板电脑上截图批注，教师可以同时呈现多名学生平板电脑上的内容，进行相互评价．师生在大量的信息面前平等交流、分享，消除传统模式下教师一言堂的现象，教师与学生都是课堂中的主体，都有所收获和成长．

案例3人教版高中数学教材必修第二册“8.4.1平面”教学课堂小结阶段．

生1：数学讲究严谨，三个基本事实是不必证明，但是今天学习的平面这个概念，到底能不能下个精准的定义？

此时一些学生陷入思考，还有些学生开始利用平板电脑在网上搜索．很快一名学生在平台上上传了在百度中的截图：数学上称最简单的面，即在相交的两直线上各取一动点，并用直线连结起来，所有这些直线构成一平面．

师：你觉得这个定义如何？

生1：它用更基本的元素“点”和“线”来定义平面，比较合理．而且，这种方法与课本中图8.4-5中提到的“直线网”的说法如出一辙．

这时进行网上搜索的学生纷纷在平台上分享自己的批注和截图，有：“所谓的平面，就是带有两个不共线的向量，且其他向量都可以用这两个向量线性表示的空间”“在空间中，到两点距离相同的点的轨迹”“指没有高低曲折的面”“平面，是指面上任意两点的连线整个落在此面上”“直线沿某一固定方向和其相反方向移动所形成的图形——我自己想的！与课本上圆柱一类的旋转体定义如出一辙，网上搜了没有这个定义(生2)”．

师：经过大家的推选，认为“在空间中，到两点距离相同的点的轨迹”最简洁有力，作为我班公认的“平面的定义”．

学生围绕中心问题展开思考、搜索资源，经历获取信息、加工信息、整合信息、发布信息的过程，又在平台上分析比较、评价，最终形成结论．整个教学活动过程中因为教师的主导，互联网中的海量信息并没有削减学生独立思考，对数据和信息的处理过程，也是培养学生信息获取能力并养成良好思维习惯的过程；正是有了“互联网+”这个平台，学生才能搜索资源，并能按需选择合适的学习路径(有的先搜结果再分析理解，有的先形成结果再搜索(生2))，完全成为学习的主人，破解了数学课堂模式化培养与个性化学习之间的矛盾；也正是有了这个平台，师生间、学生间形成学习共同体，展开了更积极主动的交流，共同促成了深度教学．

4 从经验课堂转向精准课堂，互联网成为评价工具

练习和考试是实现了解学生学习情况、查找问题、分析反思进而优化教与学的重要手段，但是目前还存在着“练得多、分析得少”“分析不及时、跟踪性分析更少”的情况．教师往往结合教学经验和批改时的印象，对一些错得多的题进行集中讲解．学情的模糊导致讲评针对性不强、效率低下，甚至存在增加学生负担的弊端．利用“互联网+”环境下的及时反馈系统(IRS)，可以在课堂上迅速作出针对全体的精准分析．

案例4抛物线的标准方程第1课时．

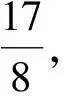
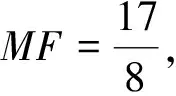
可以看出，课堂的实时数据为临时调整教学设计提供了支撑，为课后更有针对性的辅导提供了依据，也为教师反思之前的教学行为提供了可能．如果把某类题的作答数据与一段时间后同类题的作答数据作比较分析，那么这样一个大数据的积累和应用过程不仅是学生成长的“画像”过程，也是教师走向专业化的过程．

5 结语

随着互联网技术的进步，资源形态、教学场景、教学模式、评价方式有了新的变化，为教学的设计和实施提供了新的可能．然而，值得注意的是，“互联网+”只是一种工具、一种平台、一种理念，要追求互联网与数学课堂教学的深度融合，我们还需要以学生为本，不断提升自身信息技术素养，在实践中不断探索，增加案例分析研究，充分挖掘“互联网+”的环境与资源优势，让课堂的深度交流得以实现、深度学习得以发生．