盾构管片上浮量理论计算模型及上浮控制措施研究

杨志勇杨星张长旺孙正阳江玉生邵小康

中国矿业大学(北京)力学与建筑工程学院,北京 100083

盾构隧道施工过程中,管片在脱出盾尾后经常会发生局部或整体上浮,导致管片错台、开裂、渗漏水,降低隧道的整体结构强度,影响管片的防水效果,缩短隧道使用年限[1-2]。管片上浮一直是困扰工程建设人员的重大难题,因此,建立管片的上浮量理论计算模型,分析管片上浮量影响因素并采取相应的抗浮控制措施,对盾构隧道的安全和质量有着重要意义[3]。

目前,国内外相关学者普遍认为,管片上浮是盾构开挖过程中引起的地层应力释放与同步注浆过程中产生的浆液浮力共同作用的结果[4-5]。在此基础上,各种力学简化模型与上浮机理也被广泛地提出。叶飞等[6-7]认为,抵抗隧道管片上浮的抗浮力主要由管片间的抗剪螺栓接头与上覆土产生的竖向围岩应力二者的共同作用,提出了管片局部抗浮的计算方法。肖明清等[8]采用二维有限元法,考虑了地层特性和注浆材料两个因素,对管片上浮过程进行了模拟,证明了管片上浮是水及浆液压力产生浮力作用的结果。舒瑶等[9]对南宁地铁盾构区间的管片上浮量进行数据分析,发现上浮量近似服从正态分布。梁禹等[10]考虑了管片上覆浆液和土体的压缩作用对管片截面进行了力学分析,得到了地质条件、浆液质量、螺栓剪力等计算参数对管片上浮量的影响。张君等[11]对管片结构在施工过程中的受力状态进行分析,将管片上浮分为管片封闭成环上浮、盾构千斤顶推进上浮、脱出盾尾后管片上浮、浆液初凝后管片上浮。魏纲等[12]采用修正惯用法衬砌设计理论对上浮后管片内力进行计算,发现上浮后管片的弯矩、剪力和轴力均比正常设计状态下的管片内力有大幅增加。Bezuijen等[13]对隧道施工中作用在管片上的浆液压力进行现场实时监测发现,浆液压力自隧道拱顶到拱底近似按线性递增,且随浆液凝固而逐渐减小。

上述研究多集中在对管片上浮状态的受力分析,很少建立管片上浮量理论计算模型和推导管片上浮量预测计算公式。文献[6]和[10]虽然用力学分析的方法推导了管片上浮量预测计算公式,但是该公式并未在实际工程中进行计算和验证。目前,关于管片上浮量的预测多是利用软件进行数值模拟获得的。

本文对管片的受力状态进行分析,建立管片上浮量理论计算模型,推导理论计算公式,并结合北京地铁新机场线工程实例,采用计算模型对管片上浮量进行理论计算,并与工程中实际上浮量进行对比,分析理论计算模型的拟合情况,解释了该工程管片发生异常上浮的原因,并提出了控制管片上浮的措施。本研究可为管片上浮量的预测及控制提供理论借鉴与参考。

1 管片上浮计算模型

1.1 管片受力

管片在脱出盾尾后会处在同步注浆浆液中,而所受的不平衡力将导致管片产生一定的上浮,如图1所示,当管片最终处于平衡状态时,单环管片在竖直方向上的受力关系如下:

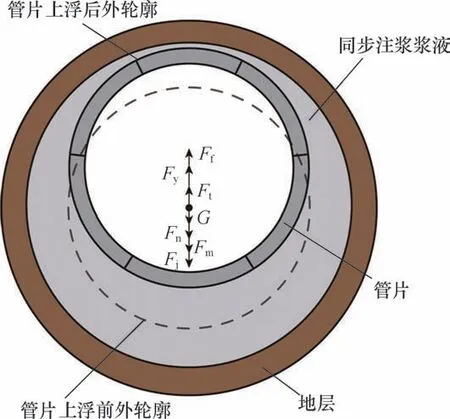
图1 管片受力示意图Fig.1 Schematic diagram of segment force

式中,Ff为管片受到的浆液浮力,kN;Fy为同步注浆产生的压力差,kN;Ft为千斤顶推力的竖向分力,kN;G为管片自重,kN;Fn为管片受到的黏滞阻力,kN;Fm为环间摩擦阻力,kN;Fj为环间螺栓剪力,kN。

(1)浆液浮力(Ff)。在无水地层的情况下,只需要考虑注浆浆液包裹管片时对管片产生的上浮力;在有地下水的地层施工时,需要考虑地下水和注浆浆液共同作用对管片产生的上浮力。要注意的是,对于高渗透性无水地层情况,还需要考虑由浆液向地层渗透所引起的浆液上浮力损失。在不考虑浆液渗透的情况下,管片浮力可由式(2)计算。

式中,π 为圆周率值;b为单环管片的环宽,m;R0为管片外环半径,m;γj为浆液容重(有水地层时,为地下水和浆液的平均容重),kN/m3。

(2)同步注浆压力差(Fy)。同步注浆压力差作为管片所受的动态上浮力,在不同的土层条件和注浆参数下的计算结果差异较大[14-15]。根据盾构同步注浆的特点,可以将左、右上侧注浆压力平均值定义为上部注浆压力均值,将左、右下侧注浆压力平均值定义为下部注浆压力均值,如图2所示。由于实际工程中盾构同步注浆压力计一般设置在注浆口,压力计所测数值除了受注浆压力影响外,还受到周围浆液压强的影响[16],因此计算同步注浆压力差需要去除管片周围浆液所造成的浮力。同样,在不考虑注浆过程中浆液会向地层渗透的情况下,同步注浆压力差为

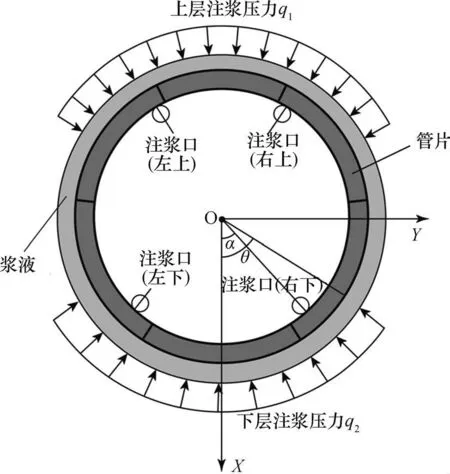
图2 同步注浆压力分布及管路布置情况Fig.2 Synchronous grouting pressure distribution and pipeline layout

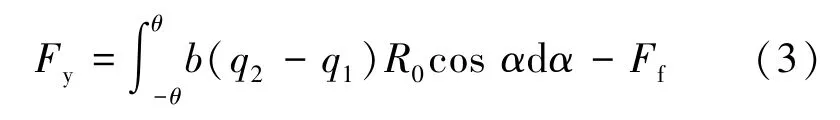
式中,θ为同步注浆角度(计算时按弧度取值),rad;q1、q2分别为管片顶部和底部注浆压力,kPa;α为管片截面的环向角度,(°)。

本文仅考虑最不利的情况,即对可能产生的最大动态上浮力进行分析。此时,取θ=π/2,则

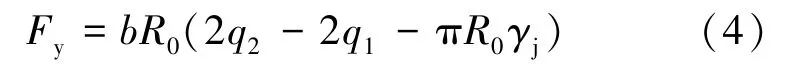
(3)千斤顶推力的竖向分力(Ft)。盾构的推力是由推进千斤顶油缸直接作用在管片上而产生的。当盾构姿态调整或纠偏时会对管片产生向下的竖向分力,根据盾构的实际推力参数,其产生的竖向分力可表示为

式中,T为盾构推力,kN,可由盾构参数获得;β为盾尾轴线与水平线的垂直方向夹角,(°)。

(4)管片重力(G)。成环管片的自重可按式(6)计算:

式中,γc为管片混凝土容重,kN/m3;R1为管片内半径,m。

(5)管片黏滞阻力(Fn)。水泥浆液可视为牛顿流体,满足牛顿内摩擦定律[17]。如图3所示,设δ1为管片与地层间的空隙宽度,取值与盾尾间隙一致。δ1对比于管片外径R0相差超过50 倍(即R0/δ1＞50),因此浆液在空隙间的流动路径可近似视为直线分布。

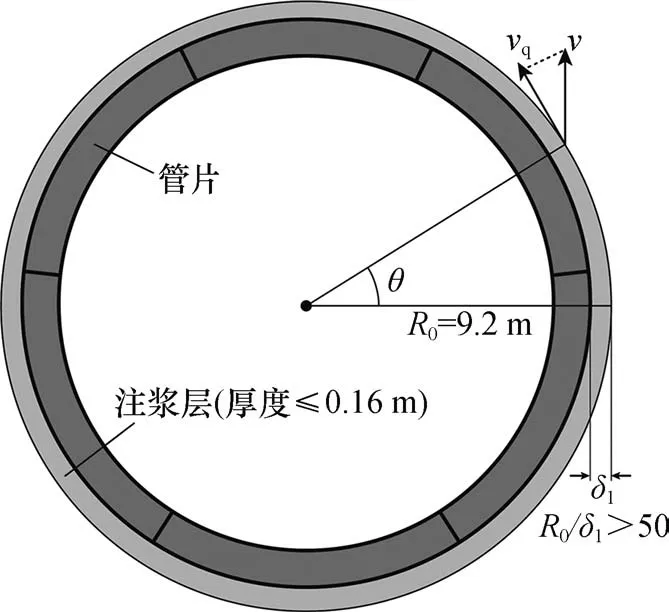
图3 黏滞阻力计算示意图Fig.3 Schematic diagram of viscous resistance calculation

管片黏滞阻力、单位黏滞阻力、管片上浮的切向速度、浆液黏度的计算如下:

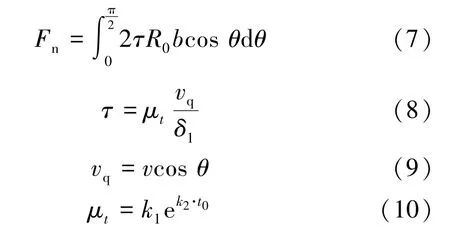
式中,τ为单位黏滞阻力,kPa;μt为浆液黏度,kPa·s;vq为管片上浮的切向速度,m/s;δ1为盾尾间隙,m;v为管片上浮速度,m/s;t0为同步注浆浆液的初凝时间,s;k1为水泥浆液黏度的时变性参数,kPa;k2为黏度的时变性参数系数,无量纲。

(6)管片环间摩擦阻力(Fm)。由于千斤顶的推力作用,管片环间会被严密挤实,其摩擦阻力可由式(11)计算:

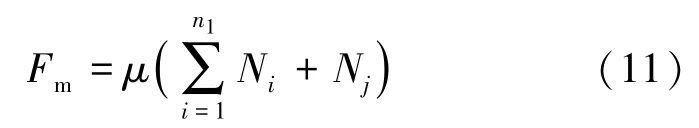
式中,n1为螺栓数;μ为摩擦系数;Ni为单根螺栓紧固所产生的压力,kN;Nj为环缝面的真实压力,kN,一般略小于非推进状态下千斤顶作用在已拼装管片环的残余推力。

(7)环间螺栓剪力(Fj)。管片在上浮过程中,相邻环间的管片会由于错台对螺栓产生一定的剪力[18]。实际工程中由于管片错台导致螺栓被剪坏现象少有发生,因此,一般情况下管片环间螺栓所承受的剪力还远达不到螺栓的极限剪力。保守估计,本文取螺栓的许用剪力(通过极限剪力与安全系数折算得到的值)作为管片上浮过程中环间的螺栓剪力,其计算公式如下:

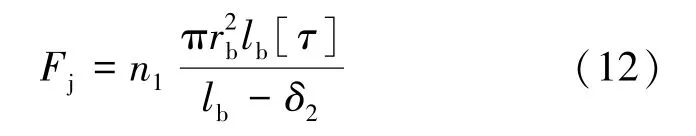
式中,lb为螺栓有效长度,m;rb为螺栓半径,m;[τ]为螺栓许用剪应力,MPa;δ2为剪力接触点间距,m。

1.2 管片上浮量

当同步注浆完成后,管片脱出盾尾后会受到未凝结浆液的浮力作用而上浮,此时开挖间隙内的浆液呈流体状态,地层的反作用力通过流动的浆液无法有效地传递到管片上[19],因此在浆液未凝结前地层应力对管片的作用可以忽略。同时,已有研究[13,20]表明,浆液初凝后(失去流动状态)的管片上浮量占总上浮量的90% 以上,且逐渐趋于稳定。故本文主要考虑并计算浆液凝结前(呈流体状态)的管片上浮量。

管片刚脱出盾尾时的上浮速度为0,此时管片受到的不平衡上浮力最大,上浮加速度也为最大值,管片开始上浮。随着浆液黏滞阻力、地层应力的不断增大,管片最终会达到受力平衡状态,即有式(1)的关系。根据牛顿第二定律加速度与力的关系,可得到管片上浮速度与受力的关系为

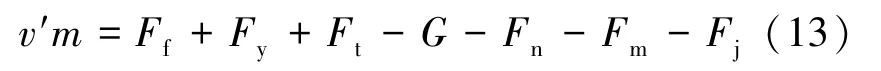
式中,v′为管片上浮的加速度,m/s2;m为成环管片的质量,kg。

将式(2)至式(12)代入式(13),联立后的结果涉及超越方程,故通过Matlab 数值拟合[21]可得

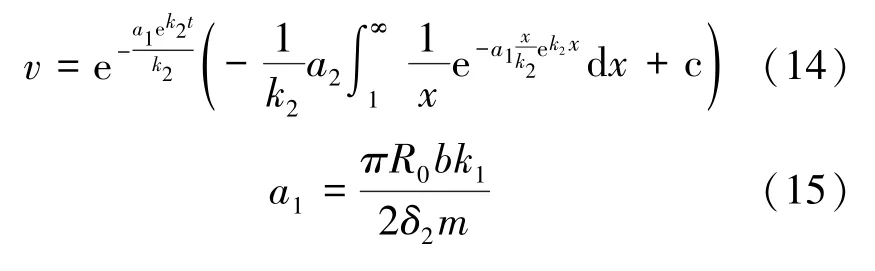
式中,c为待定常数;a1、a2为已知系数。

因此,可以得出在浆液初凝时间t0前,管片的上浮量S即为v-t的积分面积。式(14)含有积分函数,为了便于计算,取管片上浮最大速度vmax(此时管片在竖直方向上受力平衡)的一半为整个上浮过程的平均速度,故管片的上浮量S可表示为

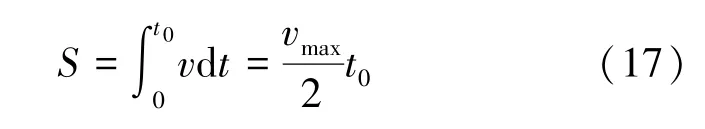
联立式(14)和式(17),考虑边界条件:t=0 时,v=0;t=t0时,v=0。得到上浮量S的解析解如下:

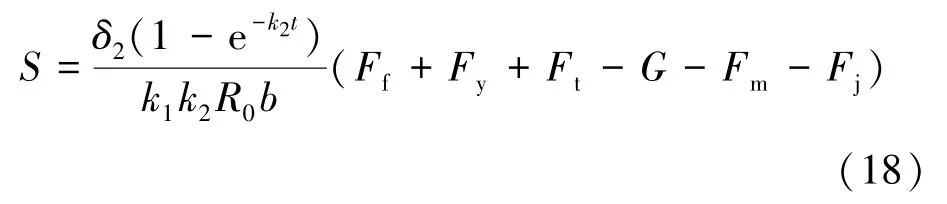
需要说明的是,式(18)是不考虑浆液向地层产生渗透力的受力平衡计算式,因此对于富水或低渗透性地层中浆液难以渗入情况的计算结果较为准确,而其他情况还需要考虑渗透力的作用。

2 工程实例分析

2.1 工程简介

北京市新机场线3 号风井至草桥站盾构区间双线总长6 120 m,隧道埋深10.7～24.6 m,最大坡度为28.5‰,最小曲线半径为700 m。盾构刀盘开挖直径9 150 mm,盾体直径9 100 mm,管片外径8 800 mm,内径7 900 mm,8 分块,环宽1 600 mm。隧道穿越地层主要为卵石层,局部为粉质黏土与卵石的混合层,地下水位位于隧道底部以上0～8.2 m。隧道前875 m 范围(0～547 环)不受地下水影响。由于本文仅对500 环以内的管片上浮数据进行了分析,因此本工程的理论计算不考虑地下水的作用,0～500 环的地质情况如图4所示。

图4 地质剖面图Fig.4 Geologic profile

2.2 管片异常上浮情况

本工程盾构施工过程中,管片未脱出盾尾时的坐标由导向系统中盾尾坐标和盾尾间隙直接算出,脱出盾尾后的管片,盾构每掘进120～160 m(75～100 环)对管片的坐标进行测量1 次。通过对比脱出盾尾前、后管片的垂直坐标,即可求得管片的最终上浮量S。

以左线盾构掘进为例,根据实测结果,323 环以前管片上浮量在40～60 mm 之间,此时盾构处于全断面砂卵石地层中;325 环时,管片上浮量迅速增大至115 mm,此时地层正由全断面砂卵石层转变为砂卵石、黏土复合层,之后330～385 环之间的上浮量基本在120 mm 左右,最大值达132 mm;385 环以后,由于采用了改善浆液质量的抗浮措施,管片上浮量有了一定的控制,其平均值在80 mm 左右。280～490 环的管片上浮量如图5所示。

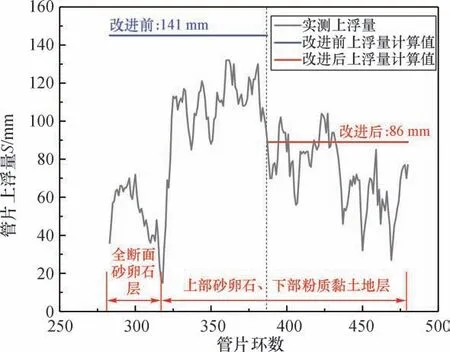
图5 280～490 环管片上浮量的实测值与计算值Fig.5 Measured value and calculated value of the floating amount of the segment between 280 and 490 rings

2.3 上浮原因分析

根据图5 的实测结果,283～315 环与316～385 环的管片上浮量差异巨大,两段地层的断面情况如图6所示。283～315 环隧道穿越地层为全断面无水卵石地层,该地层渗透系数大,同步注浆浆液注入后,浆液中的水渗入地层,进而缩短浆液浮力对管片的作用时间,增大黏滞阻力,所以管片上浮量小。而315～385 环隧道穿越地层的上部为砂卵石层、下部为粉质黏土层,由于粉质黏土层渗透系数小,管片下部浆液无法有效地向地层中渗透,其黏度和初凝时间的变化不大,故浆液浮力对管片的作用时间较长,最终导致该段的管片上浮量逐步上升。而两段区间除了地层情况变化外,施工参数、同步注浆浆液类型等均一致,因此可以推断,导致本次管片上浮量发生异常变化的主要原因是地层因素。

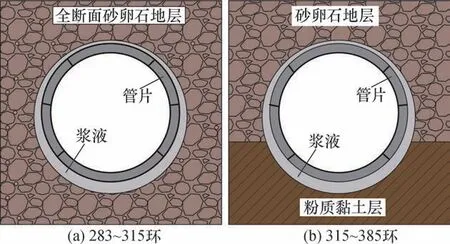
图6 开挖地层情况Fig.6 Excavated ground conditions

2.4 管片上浮量理论计算

(1)最终上浮量计算。以本工程的实际施工参数为依托,结合理论计算式(2)至式(16)对管片的上浮量进行计算,参数取值见表1。管片上浮量的理论计算结果和实测值对比如图5所示。

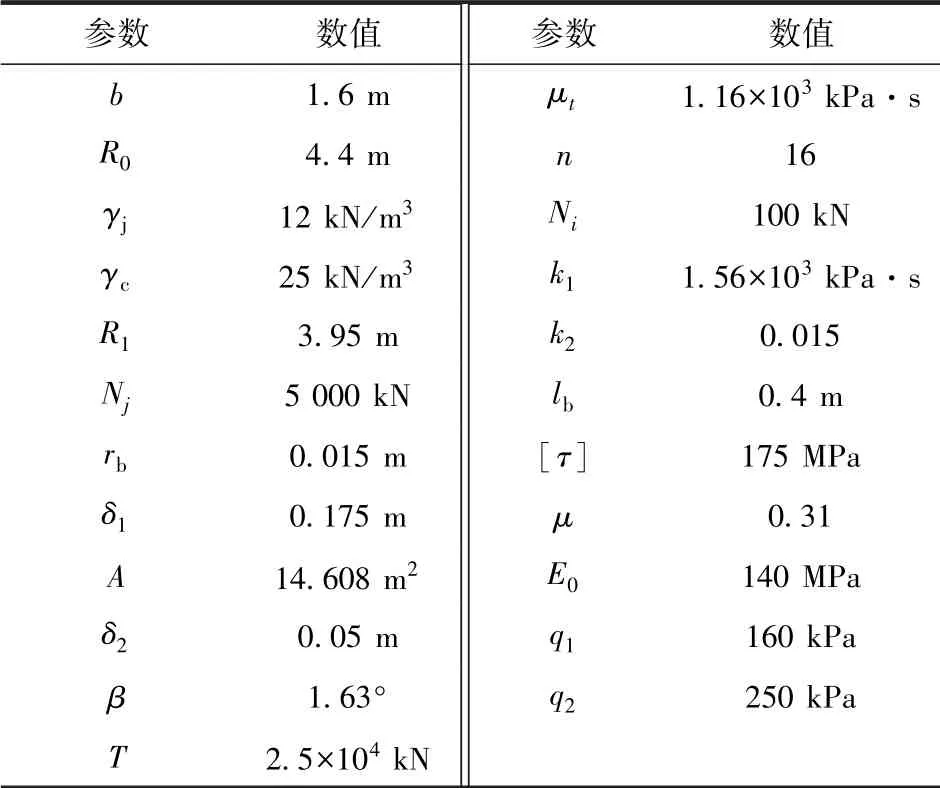
表1 管片上浮量计算参数Tab.1 Calculation parameters of the floating amount of the segment

由图5 可以看出,385 环之前的上浮量,理论计算结果比实测的最大值高13 mm(误差不到10%),这是因为理论计算过程所考虑的取值均是管片上浮最不利的情况,如同步注浆角度θ取π/2、推力T取设计参数最大值2.5×104kN、螺栓剪力[τ]取其许用抗剪强度175 kPa 等。因此,本工程对管片上浮的计算结果误差不大。

(2)上浮量与浆液初凝时间的相关性计算。浆液在不同的凝结时间具有不同的特性[22],通过理论计算,管片上浮量在不同浆液下随时间变化情况如图7所示。从任意单个曲线可以看出,管片在脱出盾尾的10 min 以内,上浮量急剧增大;至初凝时间之前,上浮量略有上升但不明显;而到达初凝时间后,管片的上浮量基本稳定。浆液的性质对管片上浮量有着较大的影响,使用改进的浆液之后,管片上浮量有了明显的降低。因此,通过缩短浆液初凝时间、增大其抗压强度和黏滞性,可以有效地降低管片的上浮。

图7 浆液改进前后管片上浮量-时间关系Fig.7 Floating amount of segment before and after slurry improvement-time relationship

2.5 上浮控制措施及效果

根据建立的管片上浮模型和推导的管片上浮量计算公式,影响管片上浮量的主要因素有地层条件、管片尺寸、同步注浆压力差、浆液性质。由于地层、管片尺寸等客观条件难以改变,而本项目盾构开挖直径较大,每环需填充浆液约7.5 m3(理论计算的地层损失空隙),如果降低注浆管压力可能导致同步注浆不足,无法完全填充开挖空隙,导致地表过量沉降,因此注浆压力维持不变。综合考虑,决定采取改进同步注浆浆液性质的方法来控制管片上浮。根据上述的管片上浮机理,浆液的初凝时间、强度指标是决定浆液质量的重要因素。因此,本文在原有配比浆液的基础上对其进行改进,改进前、后的浆液配比见表2。同时,通过单轴抗压强度和黏滞性试验,测试了改良前、后浆液在不同凝结时间下的性能指标,试验过程如图8所示,所测得的浆液强度及黏度时变性参数见表3。

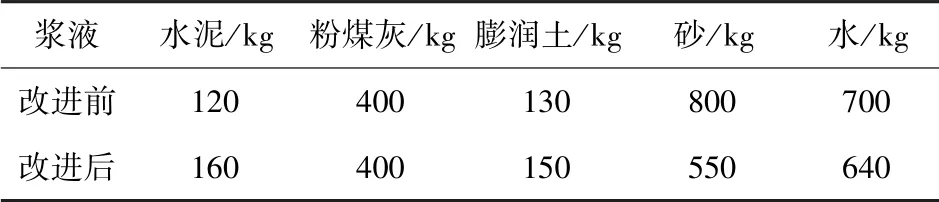
表2 同步注浆浆液配比参数Tab.2 Synchronous grouting slurry ratio

图8 浆液配比及力学特性试验Fig.8 Slurry ratio and mechanical characteristics test

表3 同步注浆浆液强度及时变性参数Tab.3 Synchronous grouting slurry characteristics and time varying parameters

将改进后的浆液应用于385 环后的施工中,由图5 可以看出,管片上浮量有了明显地减小,385～480 环的管片上浮量平均值在70 mm 左右,且最大值不超过110 mm。

3 结论

本文在分析管片在竖直方向受力状态的基础上,建立了管片上浮的理论计算模型,推导了管片上浮量计算公式,并结合工程实际,将理论计算结果与实测值进行对比,验证了计算模型的准确性。同时,对管片异常上浮原因进行了分析,提出了控制措施,主要得出了以下结论:

(1)地层的变化,尤其是地层渗透性的变化,会影响同步注浆浆液的析水性能,进而影响其黏滞性和初凝时间,导致管片的异常上浮。

(2)管片在脱出盾尾的5 min 内迅速上浮,至初凝时间之前会逐步趋于稳定,而初凝时间过后基本不再变化。

(3)通过改善浆液性能,提高黏度μt、缩短初凝时间t0可以增加浆液的黏滞阻力、减少管片上浮的时间,进而能够减小管片的最终上浮量,即采用强度增长快、初凝时间短的浆液能有效控制管片上浮。同时,还要考虑浆液的填充效果、对地层及沉降的控制以及泵送能力,避免堵管情况的发生。