采矿岩石多尺度破坏力学

左建平孙运江刘海雁于美鲁雷博宋洪强文金浩

1.中国矿业大学(北京)力学与建筑工程学院,北京 100083;2.煤炭资源与安全开采国家重点实验室,北京 100083

“十三五”期间,我国煤炭开采自主创新能力得到了大幅提升[1],矿山灾害大幅降低。“十四五”时期,我国煤矿安全生产形势依然严峻,百万吨死亡率远高于世界先进国家水平[2]。我国各大矿区煤层赋存条件存在较大差异,开采方法多样,导致岩石破坏行为及力学机理复杂多变。煤层开采后围岩应力重新分布,采空区顶板岩层出现拉伸破坏、剪切破坏或混合破坏,采空区周围产生采动支承压力,煤岩体发生压剪破坏。煤矿灾害事故频发主要是由于对采动复杂应力环境下围岩的宏细观破坏机理研究不足所致。

岩石的物理性质与测量的尺度密切相关[3]。同样地,煤矿开采根据研究对象的不同,岩石破坏力学行为的研究也存在多尺度特征,如图1所示。岩石宏细观破坏力学行为是岩层移动和巷道围岩控制的基础。岩层的破断移动影响着巷道围岩稳定,岩层破断运动产生支承压力,其峰值约为地应力的1.5～3.0 倍[4],是造成巷道破坏恶化和诱发灾害的主要驱动力。近年来,国内外学者在煤矿开采岩石破坏及控制方面进行了大量研究。谢和平[5]系统分析了深部开采煤岩失稳破坏多尺度多因素协同作用机理及演化规律。何满潮等[6]指出,深部工程岩体力学是非线性力学系统。鞠杨等[7]提出3D 模型打印与应力冻结技术相结合的方法,研究地下岩体内部复杂结构与三维应力场分布的定量表征与可视化。许家林等[8]研究了关键层对覆岩大尺度破断影响,并提出了预测导水裂隙带高度的新方法。

图1 采矿岩石多尺度破坏行为Fig.1 Multi-scale failure behavior of rock in mining engineering

在前人研究的基础上,笔者对岩石宏细观破坏力学机理、采动覆岩破断运动规律、巷道围岩控制进行了系统研究,基于宏细观力学试验揭示了围岩渐进梯度破坏机理,提出了采动覆岩移动“类双曲线”模型,建立了煤矿巷道围岩等强支护理论,并提出了巷道全空间协同控制技术[9-13]。以期为我国煤矿开采灾害防治提供理论和技术支持。

1 采矿岩石宏细观破坏力学

岩石作为天然地质材料,其宏观力学行为是人们最初研究的重点,而岩石材料的强度、变形和破坏特性不仅与外力作用条件相关,而且极大地受到其内部细观结构的影响[13]。因其内部同时存在大量微裂纹、微孔洞等细观缺陷和非矿物杂质,使得岩石呈现显著的不连续性、不均匀性和各向异性等特征。因此国内外学者普遍认为,岩石损伤和破坏现象是从细观到宏观的多尺度耦合的过程[14-16]。目前,岩石的宏细观破坏机理已成为岩石力学领域研究的热点、难点问题,得到了各国相关领域学者的高度重视。谢和平等[17]对岩石断口形貌进行了详细分析,深刻揭示了岩石的破裂机理。崔振东等[18]利用SEM 扫描电镜进行了页岩的细观拉伸原位试验,获得了微裂纹的起裂、扩展及止裂规律。朱其志等[19]建立了非线性力学行为的损伤-摩擦耦合细观本构模型。李术才等[20]利用电阻率和声发射技术研究了单轴压缩下砂岩的破坏过程和力学响应。尹光志等[21]研究了粗砂岩宏观力学特性与围压的关系。近年来,笔者对采矿岩石力学中岩石宏细观多尺度破坏问题也进行了系统研究。

1.1 岩石细观破坏行为

利用带加载装置的SEM 高温试验系统对岩石细观裂纹的萌生、扩展和断裂全过程及其断裂机制进行了系统研究[22-26]。平顶山砂岩经不同温度热处理后细观断裂试验,如图2所示。经过50 ℃、100 ℃热处理后的砂岩,裂纹均是沿着颗粒的边界向前扩展,属于绕行方式,断裂属于沿颗粒断裂。而经过125 ℃和150 ℃热处理后的试件,裂纹不仅有沿颗粒边界扩展,同时伴有穿矿物颗粒扩展的方式,断裂属于穿颗粒断裂和沿颗粒断裂的细观机制共同作用。我们认为,125 ℃是砂岩三点弯曲裂纹扩展方式发生变化的临界温度点。断裂韧性与温度的关系如图3所示,25 ℃～200 ℃之间砂岩的断裂韧性随着温度的变化规律不太明显,125 ℃是平顶山砂岩断裂韧性达到最大值的温度,也是砂岩在该温度附近产生不稳定性的临界温度。

图2 不同温度热处理后砂岩断裂的裂纹扩展模式[26]Fig.2 Crack propagation mode of sandstone fracture after heat treatment at different temperatures[26]

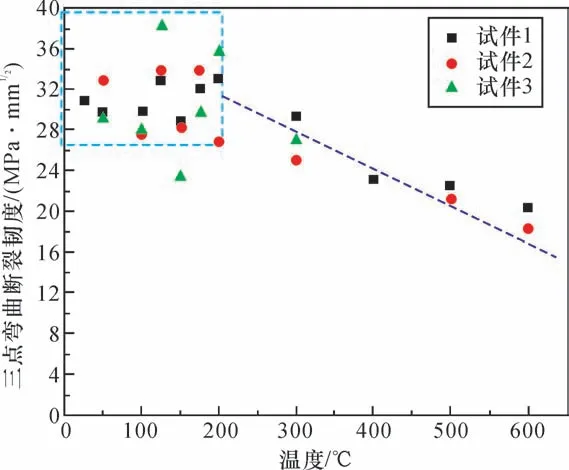
图3 温度对砂岩断裂韧度的影响[26]Fig.3 Influence of temperature on fracture toughness of sandstone[26]

由于砂岩是由多种矿物颗粒及黏土胶结物组成的,这些矿物颗粒的大小存在差异。经过不同温度热处理后,矿物颗粒之间及其与黏土胶结物的结构形式发生变化,部分吸附水和层间水的蒸发明显改变黏土胶结物的黏结性能。而矿物颗粒及黏土胶结物由于其热膨胀差异,在冷却后导致矿物颗粒之间及其与胶结物之间都存在残余应力。这可能是导致不同温度断裂模式发生变化的根本原因。

1.2 煤岩体宏观破坏行为

对尺寸为φ50 mm×100 mm 的煤(M)、岩(R)、煤-岩组合体(MR)、岩-煤组合体(RM)和岩-煤-岩组合体(RMR)进行了一系列宏观破坏压缩试验[27-29]。不同组合类型试样单轴压缩下的破坏形态如图4所示。可见,煤岩组合体破坏主要发生在煤体部分,煤体以劈裂破坏机制为主。图5 为煤岩组合体与煤单体的单轴抗压强度及弹性模量变化。煤岩组合体的承载强度增大,弹性模量也变大,其中RMR 煤岩组合强度及弹性模量最大,RM、MR依次稍小。不同围压下煤岩组合体的弹性模量如图6所示,围压由0 增至15 MPa 时,组合体的割线模量大致为线性增大,当继续增大围压,割线模量基本保持不变。

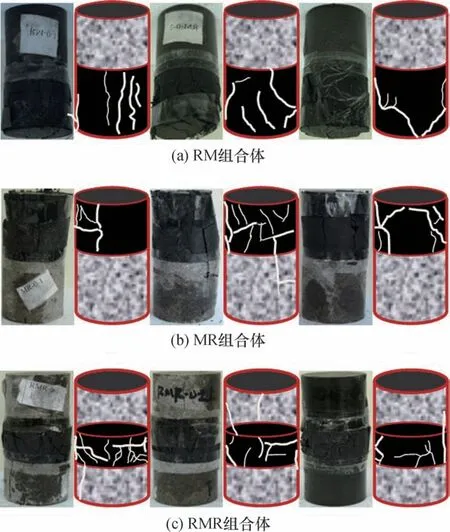
图4 煤岩组合体破坏特征[30]Fig.4 Failure characteristics of coal-rock combined body

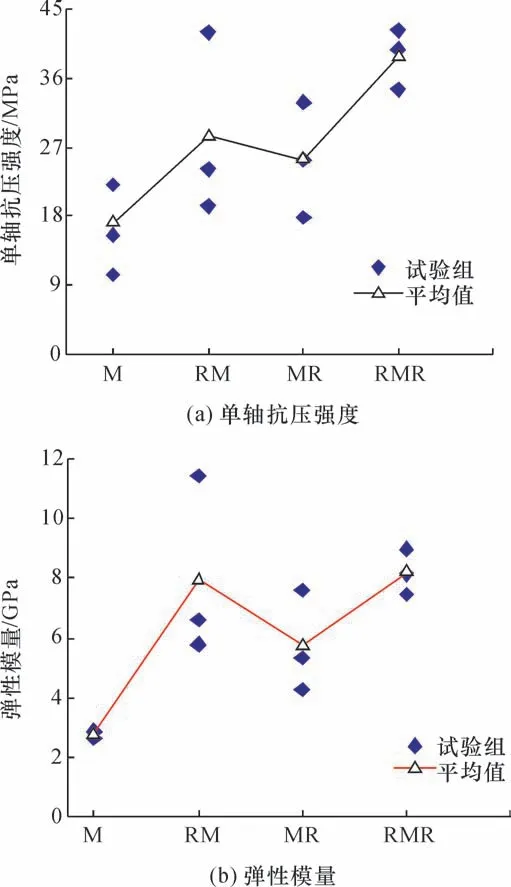
图5 煤岩组合体平均单轴抗压强度和弹性模量[30]Fig.5 Uniaxial compressive strength and elastic modulus of coal-rock combined body

图6 煤岩单体及组合体割线模量与围压的关系[31]Fig.6 Relationship between secant modulus and confining pressure of single coal rock and combined body

对煤岩组合体的循环加卸载特性进行了系统研究[32-33],弹性模量和能量特性随不同循环加卸载次数的演变规律,如图7 和图8所示。煤岩组合体的能量演化具有明显的非线性特征。根据应力梯度理论,开展了砂岩加卸载试验[34-36]。各个应力梯度区下砂岩加载全过程内部裂隙变化率与轴向应力的关系如图9所示。其中,岩石内部裂隙变化率通过测试超声波速变化反演获得。离巷道越近,岩石峰值附近裂隙变化不稳定性加剧,而破坏后裂隙迅速增多,砂岩结构变得更为复杂。

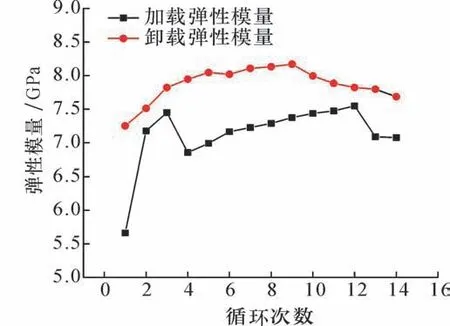
图7 不同循环次数煤岩组合体的加卸载弹性模量[32]Fig.7 Load-unload elastic moduli of coal-rock combined body for different cycles

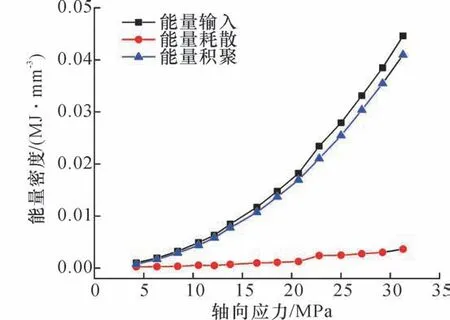
图8 循环加卸载下煤岩组合体能量演化特征[33]Fig.8 Energy evolution characteristics of coal-cock combined body under cyclic loading-unloading

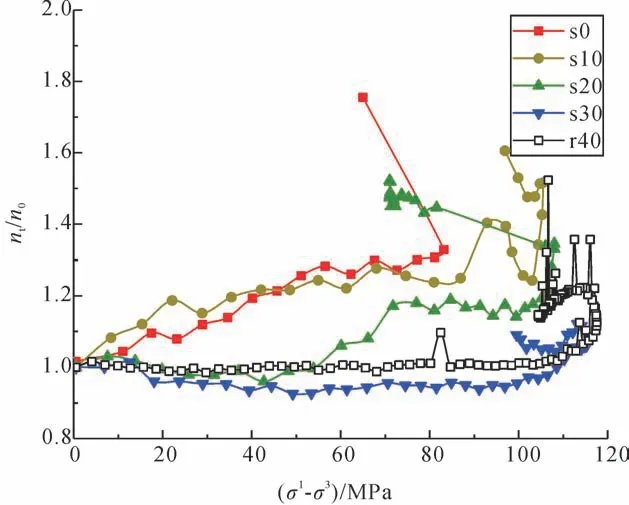
图9 不同应力梯度区下砂岩加载全过程裂隙变化[34]Fig.9 Crack variation of sandstone in the whole loading process under different stress gradient zones

1.3 煤岩体宏观破坏本构模型

煤岩体的本构关系是分析其变形破坏的基础。煤岩体内分布有大量原始微裂纹,在荷载作用下这些微裂纹以及新生裂纹的演化规律与煤岩体的变形行为密切相关。如何准确描述煤岩体内裂纹的闭合、扩展规律,是建立煤岩体变形破坏非线性模型的前提。图10 展示了单轴加载下岩-煤-岩(RMR)组合体的轴向裂纹演化规律。基于自然应变和工程应变的概念,通过推导得到了煤岩体轴向裂纹闭合模型(ACCM)和轴向裂纹扩展模型(ACPM)[37]:

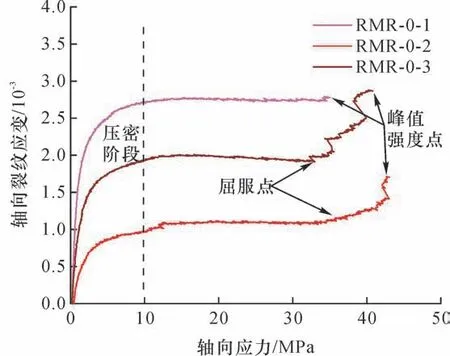
图10 轴向裂纹应变随轴向应力演化曲线[37]Fig.10 The evolution laws of axial crack strain with axial stress

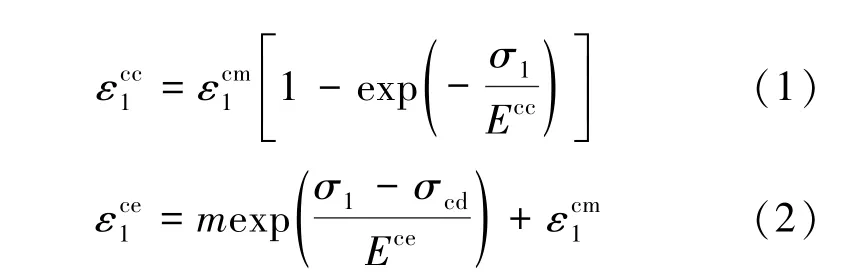
对于卸载条件,轴向裂纹是逐渐张开的,轴向应力逐渐减小。因此,若以压缩为正,则裂纹轴向张开应变与卸载轴向应力同为负值。为简要说明,以MR-C-2 试样第7 循环的卸载曲线为例,如图11所示,其中分别为裂纹开始张开和卸载结束时的轴向裂纹应变,σcri为轴向裂纹张开应力。通过将坐标原点平移,采用与加载条件下相同的推导,可得到卸载条件下煤岩体轴向裂纹张开模型(ACRM)[38]:

图11 卸载条件下轴向裂纹张开应变与轴向应力关系[38]Fig.11 Axial crack recovery strain versus axial stress under unloading condition

选用单轴加载下岩-煤(RM)组合体实验数据对煤岩体轴向裂纹闭合、扩展模型进行验证,实验数据和理论曲线如图12所示。可以看出,利用轴向裂纹应变模型计算的理论曲线与实验数据吻合度较高,较好地描述了煤岩体峰前加卸载过程中裂纹闭合、扩展的非线性行为。进而可得到煤岩体单轴加载下峰前应力-应变关系模型,见式(4)[37]。图13 展示了单轴加载下岩-煤(RM)组合体试验数据与理论曲线的对应关系,可以看出,该模型能很好地体现出煤岩体峰前应力-应变的3 个阶段,即压密阶段、弹性阶段、屈服阶段。

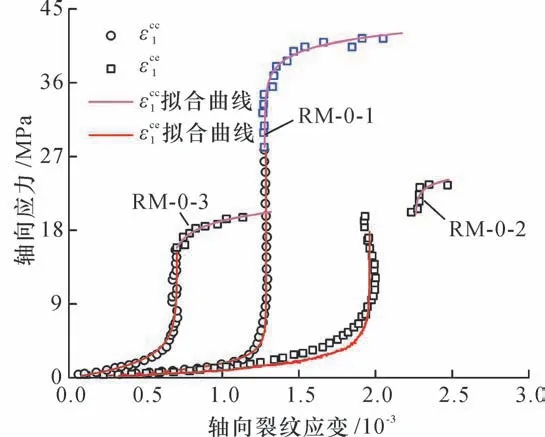
图12 峰前轴向裂纹应变模型验证[37]Fig.12 Verification of pre-peak axial crack strain models

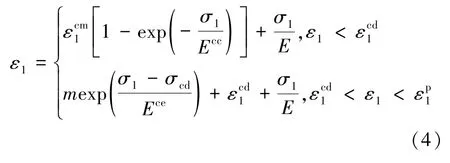
图13 峰前应力-应变关系模型验证[37]Fig.13 Verification of pre-peak axial stress-strain models

煤岩体在单轴加载下的脆性特征通常比较明显,而随着围压增大,其峰后破坏延性逐渐增强,并出现一定的残余强度。通过引用断裂力学中有序多裂纹体的概念,将峰后阶段的煤岩体概念化为裂纹体和基体两部分(图14)。

图14 三轴压缩下煤岩体峰后阶段变形分析模型[39]Fig.14 Model of post-peak deformation analysis for coal rock body under tri-axial compression

裂纹体部分由于内部含有大量裂纹,在峰后荷载作用下会发生较大的非弹性变形,并假设大量裂纹的等效变形代表裂纹体的变形。基体部分由基质颗粒构成,假设其峰后阶段的变形仍为弹性变形。由于裂纹体发生的变形较大,故其应变需用自然应变来表示,而基质的变形仍采用工程应变表示。

图15 展示了围压5 MPa 时的煤-岩(MR)组合体峰后轴向裂纹应变演化规律。根据图15 中峰后轴向裂纹应变演化规律,通过推导得到了煤岩体峰后应力-应变关系模型[39]:

图15 峰后轴向裂纹应变演化规律[39]Fig.15 The evolution laws of post-peak axial crack strain

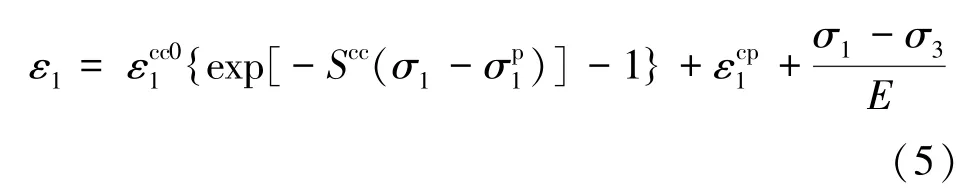
式中,εcc01 为裂纹峰前扩展阶段结束时的极值应变;为峰值点处的轴向裂纹应变;Scc为裂纹体的等效非弹性柔度。

选取常规单、三轴加载下煤-岩组合体实验结果对该模型的可行性加以验证,如图16所示。可看出,利用煤岩体峰后轴向裂纹应变模型拟合的峰后应力-应变关系曲线与试验曲线的趋势大体相同,能较好地反映煤岩体峰后阶段的软化过程和残余强度。该模型虽然对峰后延性较强试样的拟合效果较好,但对峰后脆性跌落明显的试样拟合效果较差。故该模型更适用于三轴压缩的情况。

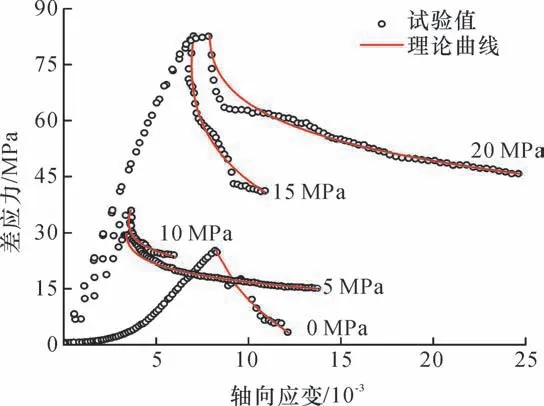
图16 峰后应力-应变关系模型验证[39]Fig.16 Verification of post-peak axial stress-strain models

1.4 岩层大尺度破断行为模拟试验

通过采空区顶板破断模拟实验装置研究了不同厚度顶板的大尺度破断模式[40](图17)。将实验结果归结为4 种破断模式[41]:①沿长边的横向“O-X”破断形态;②沿短边的纵向“O-X”破断形态;③沿长边的横向“O-”破断形态;④沿短边的纵向“O-”破断形态。基于中厚板理论建立四边简支厚顶板断裂力学模型,工作面长度和推进步距取定值,探讨岩层厚度对顶板断裂力学因素的影响。研究发现,随着岩层厚度增加,横向剪应力的作用不断增强,岩层更易发生剪切破断。工作面长度和推进步距一定时,可以得到厚硬岩层破断模式分区[42],如图18所示。随着岩层厚度的增加,岩层破断时经历了拉破坏→拉剪破坏→剪破坏,这反映了诱发岩层破断的力学因素随岩层厚度增加的演化过程。

图17 相似材料模拟不同厚度顶板破断及裂纹发育情况Fig.17 Development and failure of cracks of roof strata by similar material simulation

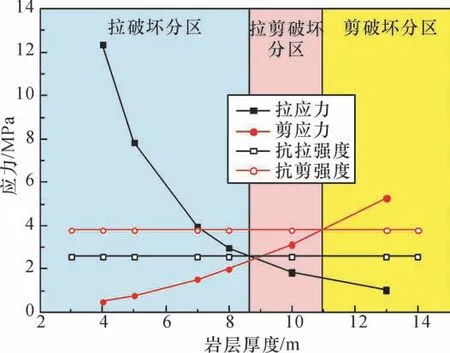
图18 厚硬岩层破断模式分区Fig.18 The thick hard rock strata breaking mode partition

2 巷道等强支护理论及全空间控制技术

地应力和采动应力是巷道围岩变形的根本驱动力,围岩力学特性是影响巷道变形的重要因素[43]。为了控制巷道变形,国内外学者提出一系列的支护理论和围岩控制技术。侯朝炯等[44]揭示了巷道锚杆支护围岩强度强化机理。康红普等[45-46]提出了巷道围岩关键圈理论和“支护-改性-卸压”协同控制技术。何满潮等[47]发明了恒阻大变形锚杆/索支护技术。于学馥等[48]提出了轴变论和围岩稳定轴比三规律。高延法等[49]提出了软岩巷道钢管混凝土支护技术。

在前人的基础上,笔者团队揭示了巷道围岩应力梯度破坏机理,建立了巷道等强支护理论,提出了全空间协同控制技术[50],实现了巷道围岩均匀可控变形。

2.1 煤矿围岩应力梯度破坏机理

本团队基于现场、室内宏细观破坏实验及数值分析,认为应力梯度是导致巷道围岩破坏的一个重要影响因素,建立了相应的巷道围岩应力梯度破坏理论模型[12],如图19所示。深部巷道围岩破坏和所处的应力梯度场有很大关系:靠近巷道的区域相对应力梯度越大则应力贡献度越小,该处岩体容易发生破坏;离巷道较远时,相对应力梯度接近零,而应力贡献度上升,则趋于稳定。这是对围岩松动圈理论的进一步发展。

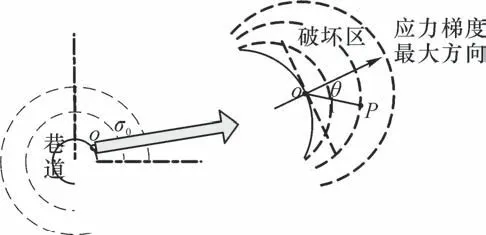
图19 围岩梯度破坏模型Fig.19 Model of rock damage spot

根据井巷围岩应力弹性和弹塑性状态的理论解,在不同深度的环境进行岩体开挖时,巷道埋深对巷道周围应力分布的影响[12]如图20所示。由图20 知,巷道开挖导致围岩切向应力和径向应力均发生了显著变化,越靠近巷道壁的围岩受到的切向应力越大、径向应力越小;随着距离的增加,切向应力逐渐下降、径向应力上升,二者都接近一个定值并且大小趋于平稳,即巷道的开挖对远处的岩体几乎无影响。

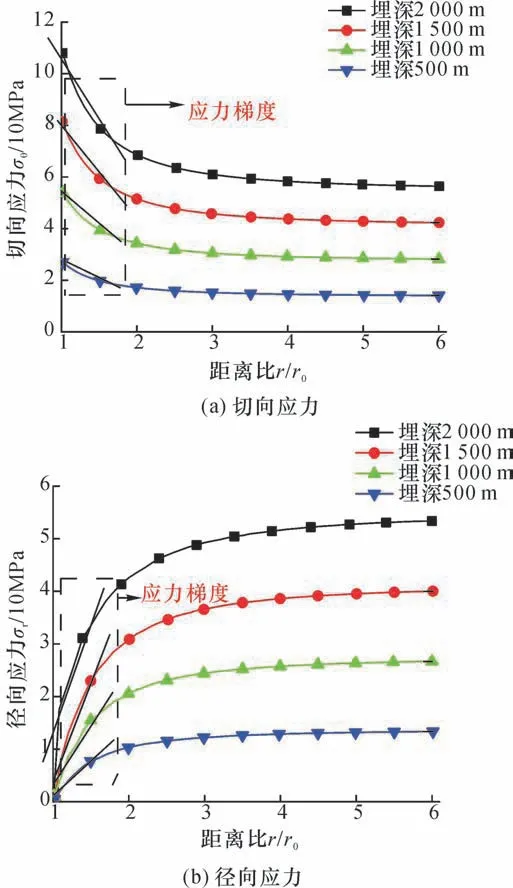
图20 巷道开挖后围岩应力分布Fig.20 Stress distribution of tunnel surrounding rock after excavation

2.2 煤矿巷道等强支护理论力学分析

基于“等强度梁”概念,我们提出了深部巷道等强支护控制理论模型[51]。根据巷道围岩受力特征,通过开槽卸压、注浆加固、锚杆(索)主动支护、钢管混凝土被动支护等综合手段,有效调整巷道围岩的应力状态,以期实现不同位置围岩能够达到安全且与地应力比相匹配的等效应力强度状态,获得应力分布形态趋于均匀、围岩塑性区范围相似的理想状态,如图21所示。提出巷道围岩全空间协同控制技术,阐释煤矿巷道全空间协同控制力学原理与控制技术,有效解决了深部巷道的大变形问题。

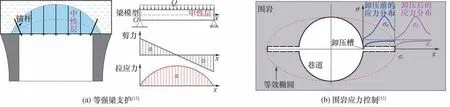
图21 巷道加固方式示意图Fig.21 Schematic diagram of roadway reinforcement methods

依据巷道破坏模式,当出现围岩应力集中、围岩破碎、拉应力区等情况时,应合理采用应力控制、注浆加固、喷射混凝土、锚杆(索)、钢管混凝土支架及全空间协同支护等措施,调整并控制围岩受力。在理想情况下,通过选取合理的控制措施让巷道周边围岩趋于均匀受压,以期实现不同位置围岩能达到安全且与地应力比相匹配的等强状态,如图22所示,此时围岩能够均匀协调变形,从而实现对巷道围岩的有效控制。

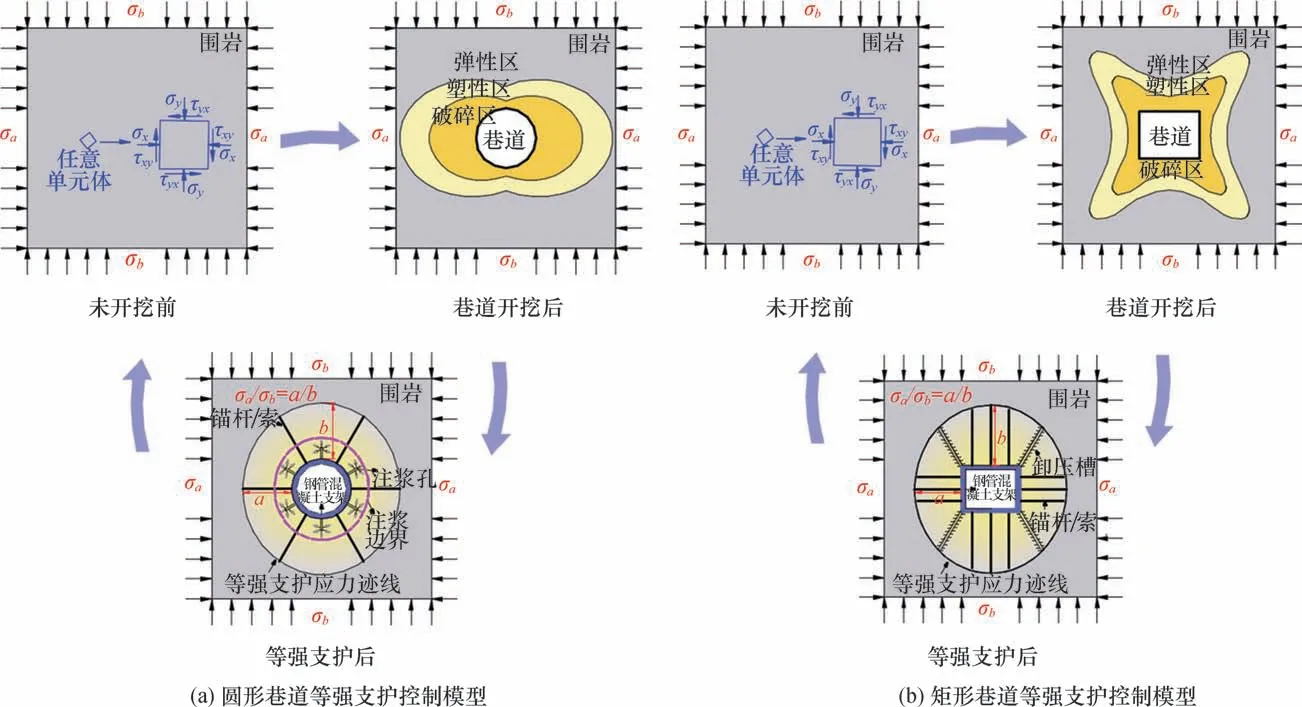
图22 巷道等强支护控制理论模型Fig.22 Schematic diagram of conceptual model of uniform strength support control theory

2.3 巷道全空间协同控制技术

全空间协同控制技术的基本核心为“全空间支护、刚柔协同、让压释能、动态监测、局部加强”[53]。该技术是指对巷道围岩空间不同破坏程度区域采取差异化强度支护,巷道完成支护后进行围岩变形动态监测,对潜在风险区域进行局部加强支护。

采用FLAC3D模拟分析单体锚索、传统桁架和全空间桁架支护的预应力场情况。当预紧力为150 kN 时,单体锚索、传统桁架和全空间桁架的预应力场如图23所示。从图23 可知,全空间桁架的最大预应力明显高于传统桁架和单体锚索,比传统桁架的最大预应力提升了11%,比单体锚索提升了38%。

图23 不同支护方式预应力场(预紧力150 kN)[53]Fig.23 Numerical prestress field of different support methods when the preload is 150 kN

现场应用中,以山西省新元矿为例,巷道围岩破碎程度极高,岩石强度较低,围岩自承载及稳定性差。原有的支撑方案强度和刚度较弱,围岩变形大,如图24(a)所示。采用高强钢管混凝土支架+锚网索喷主被动全空间协同支护技术后,软岩巷道大变形得到有效控制,如图24(b)所示。

图24 钢管混凝土支护效果[54]Fig.24 The support effect of concrete-filled steel tube

3 采动覆岩整体移动“类双曲线”模型

我国各大矿区煤层赋存的覆岩条件多样化(部分矿区出现巨厚砾岩、坚硬厚顶板和厚松散层等特殊覆岩条件),采动覆岩破断运动复杂,难以统一理论描述。目前深部开采覆岩内部的破断运动规律仍然是一个“黑箱”[55],严重制约了国家发展改革委和国家能源局倡导的“科学采矿”。采动覆岩破断运动描述是涉及采矿、力学、数学等学科的交叉性课题。在采动覆岩的破断运动方面,国内外学者进行了大量研究。Litwiniszyn 引入随机介质理论预测地表沉陷,后由刘宝琛等发展为概率积分法,已广泛应用于矿山工程的地表移动和变形预计[56]。同时,刘宝琛等[57]指出概率积分法对岩层移动的力学机理解释存在不足,对岩层内部的移动规律解释不细微,因此“需要把力学方法与几何学方法结合起来,全面描述开采沉陷的形态和过程”。钱鸣高等[58]提出了关键层理论,为岩层移动研究提供了统一的思想和方法。

基于上述研究,笔者团队先后建立了岩层移动“类双曲线”模型及内外“类双曲线”模型,分析了“类双曲线”模型随关键层层位和煤层倾角变化的演变规律,初步形成了采动覆岩移动“类双曲线”理论框架[59-66],为丰富科学采矿的岩层移动及地表沉陷控制提供了理论基础。该理论模型能够为岩层移动与控制、煤与瓦斯共采、地下水保护、充填开采等提供指导,得到国内外矿业领域知名学者的积极评价。

3.1 岩层移动“类双曲线”模型

采动覆岩整体移动“类双曲线”模型,如图25所示。主关键层上部软弱岩层发生近似“漏斗形”移动,下部坚硬基岩发生近似“倒漏斗形”破断移动,主关键层成为覆岩中破坏最窄的岩层,“类双曲线”顶点大约位于主关键层位置。“类双曲线”模型将地表“漏斗形”沉陷和顶板“倒漏斗形”破断统一成一个整体。“类双曲线”模型是关键层理论的进一步发展和应用。

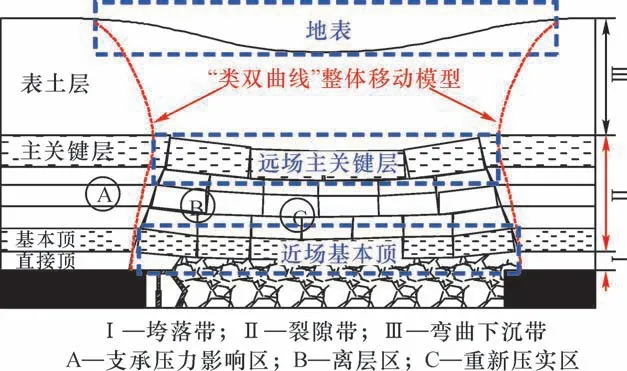
图25 充分采动覆岩整体移动“类双曲线”模型[68]Fig.25 Analogous hyperbola model of overburden movement caused by full mining

在岩层移动“类双曲线”模型的基础上,我们进一步发展了内外“类双曲线”模型,如图26所示。地表沉降与岩层移动在纵方向的变化轮廓,通过岩层移动边界与地表沉降边界构成的“类双曲线”模型描述。外“类双曲线”模型指的是岩层移动边界“类双曲线”模型,在工作面的中垂线附近似“左右”对称关系。内双曲线和外双曲线统称为厚松散层、水平煤层、开采岩层移动与地表沉降的内、外“类双曲线”整体模型。内“类双曲线”模型指的是充分采动过程中覆岩倒漏斗拱式垮落带、拱式裂隙带与地表漏斗式沉降移动拱曲线的整体描述。

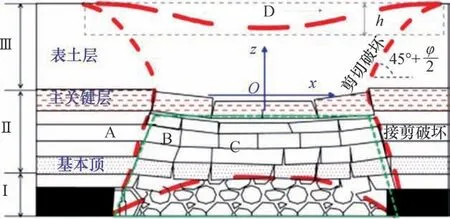
图26 岩层移动内外“类双曲线”整体模型[59]Fig.26 Conjugate analogous hyperbola model of strata movement and surface subsidence

3.2 岩层移动“类双曲线”模型演化

采动覆岩的破断运动形态与开采条件、覆岩特性等密切相关。笔者研究了不同覆岩条件下岩层移动“类双曲线”模型演化规律[61-63]。根据上覆岩层力学特性和关键层的位置,将岩层移动“类双曲线”模型分为三大类,给出了不同开采条件下“类双曲线”演化模型的判定方法和流程,传统“类漏斗”模型为“类双曲线”模型在特定覆岩条件下的一种拓扑演化形态。建立了含有主关键层位置和覆岩力学特性等参数的物理表征方程,实现了运用力学与数学方法综合描述岩层移动的整体形态。

4 结论

(1)采矿工程中,岩石的破坏与岩石的微观结构、矿物颗粒及其胶结程度密切相关。可以认为,采矿岩石力学问题就是岩石的多尺度破坏问题。该问题的研究,可将岩石的整体性质与其内部微观结构、矿物颗粒性质等的特点联系起来。

(2)在岩石力学室内实验尺度,利用带加载装置的SEM 高温试验系统研究了岩石细观裂纹的萌生、扩展和断裂全过程及其断裂机制;对不同开采(加卸载)条件下煤岩体及煤岩组合体宏观破坏力学特性进行了系统试验研究;采用相似材料模拟研究了不同厚度顶板的破断模式,得到顶板4 种破断模式和破断模式分区。

(3)在巷道围岩尺度,建立了煤矿巷道围岩应力梯度破坏模型和等强支护理论;提出了巷道围岩全空间协同控制技术,阐释了巷道全空间协同控制力学原理,数值模拟对比分析了单体锚索、传统桁架和全空间桁架预应力场的差异;现场应用有效控制了巷道围岩大变形。

(4)在采场岩层破断尺度,基于岩层移动关键层理论,建立了岩层移动“类双曲线”模型及内外“类双曲线”模型;分析了“类双曲线”模型随关键层层位和煤层倾角变化的演变规律,初步形成了采动覆岩移动“类双曲线”理论框架,丰富了科学采矿理论体系。