波形钢腹板支架支护技术的研究进展综述

吴丽丽王慧徐翔武海鹏赵卫平

中国矿业大学(北京)力学与建筑工程学院,北京 100083

巷道是井工煤矿开采的必要通道,畅通、稳定的巷道是煤矿安全、高效开采的保障。巷道围岩常常会由于岩性变异、构造变异等出现冒顶、底鼓、大变形等地质灾害,特别是软岩大变形地质构造。地下工程软岩问题自20世纪60年代以来就作为世界难题备受关注[1-3]。由于软岩本身的可塑性、膨胀性、流变性和易扰动性等力学属性[4],以及巷道初期来压剧烈,采用硬岩的常规支护手段无法适应其变形特点,过去几十年国内外学者在软岩隧道(巷道)的支护方面做了大量的试验和理论研究工作[3-8],逐渐形成了锚喷、锚网喷、预应力锚索支护、金属钢架支护等技术[9-13]。

在金属支架方面,国内外一般用矿用工字钢和U 型钢作为支护材料。20世纪80年代,英国、德国、法国、俄罗斯、波兰等国针对不同的围岩采用不同类型的金属支架,金属支架用量约占支护总量的70% 左右[14]。矿用工字钢是井下巷道支护的专用型钢,其中,Yan 等[15]采用工字形钢支护,建立了巷道支护及围岩稳定性的力学模型;姚社军等[16]运用设计约束、模糊决策及计算机技术对矿用工字钢截面进行了优化设计;寇玉昌等[17]详细介绍了新型矿用工字钢的设计、试验和井下应用情况。我国过去采用工字钢支架的数量甚多,但刚性支架与围岩的变形不相适应,U 型钢可缩性支架因结构承载力较大、可缩性能较好[18]逐渐发展起来。其中,Tan 等[19]提出一种基于泡沫混凝土和U 型钢的联合支护体系,以减小U 型钢收缩量,用于软岩巷道中。德国、波兰、前苏联使用U 型钢支架数量均占金属支架的90% 以上,我国从1963年开始使用U型钢可缩性支架,学者对U 型钢支架进行优化设计,提高其在冲击地压矿井巷道、软岩大变形巷道中的支护性能[20-23]。目前广泛使用的支架形状主要以拱形为主,张峰[24]介绍了斜腿圆拱型、直腿底拱全封闭型及马蹄形U 型钢支架的设计;Zhao等[25]提出一种封闭式U 型钢拱支架,通过数值计算和有限元分析验证该支架的有效性,并在实际工程中得到应用。U 型钢或工字钢虽然能在一定程度上解决巷道支护问题,但是它们的支护承载力不足,容易产生失稳破坏,有时巷道需要分作两跨支护,同时钢棚一般采用对棚组合,导致支护成本和施工难度大幅提高。

钢管混凝土支架作为一种新型组合支护结构成为地下工程支护中承载力较高的类型。臧德胜等[26-27]对钢管混凝土支架进行了试验研究和有限元分析,并在现场进行了工业性试验。一些专家[28-34]深入开展了圆形断面、套管连接方式的钢管混凝土支架试验,测试了钢管混凝土支架的变形曲线、极限荷载、极限变形量和失稳破坏方式,并结合实际工程研究了钢管混凝土支架施工工艺。但钢管混凝土支架总体造价较高。

近年来,随着开采深度、煤矿规模与产量的不断提高,采掘设备大型化、重型化,改变了回采巷道的整体结构状态和赋存条件,巷道埋深越大,要求的巷道断面、支承压力越大,对支护技术的要求越高。

针对巷道大变形难题,笔者将广泛用于建筑结构中的波形钢腹板工型构件[图1(a)]引入到地下工程支护结构中[35],发明了一种新型波形钢腹板支架结构[图1(b)]。它具有以下优点[36-37]:

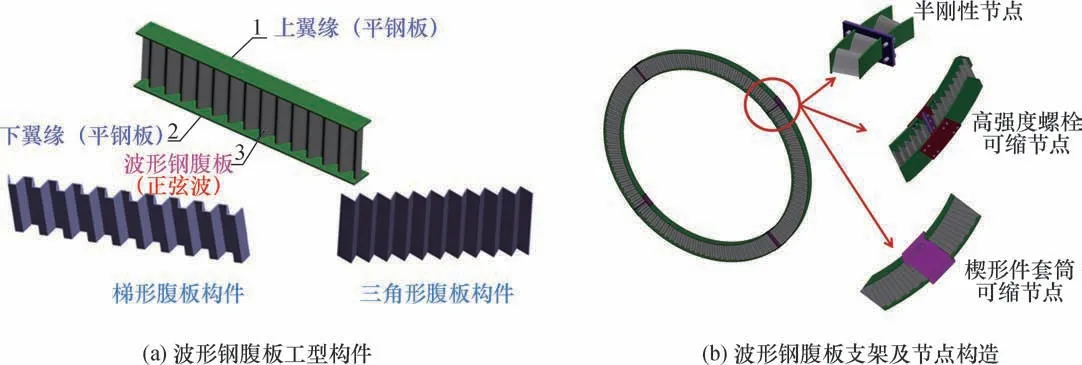
图1 波形钢腹板构件示意图Fig.1 Diagram of corrugated steel webs

(1)波形钢腹板具有较高的抗剪承载力,在较大的高厚比条件下也不易发生屈曲。

(2)支架形状在围岩压力下的稳定性能良好,其最突出的优点是腹板的波浪形构造类似“手风琴”,配合可缩性节点构造,可适应软岩的大变形而产生轴向变形。

(3)自重轻,安装就位方便,经济性好。可降低井下工人的劳动强度,提高劳动生产率,同时节约原材料、降低能耗,且巷道服务期满可拆卸,资源可回收,从而实现良好的社会经济效益。

本文主要介绍不同断面形式波形钢腹板支架整体稳定承载性能及相对传统支架的优势,支架结构的局部稳定性能,可缩性节点的试验研究以及支架与围岩的相互作用等,并探讨未来在波形钢腹板支架支护体系方面可继续拓展的研究方向。

1 波形钢腹板支架的优势对比

为了衡量波形钢腹板支架相对其他类型支架的优势,本文对波形钢腹板支架与矿用工字钢支架在不同荷载组合工况下的承载力进行了对比[38]。表1 以9 号、11 号和12 号矿用工字钢支架为例,按照相同用钢量的原则反算波形钢腹板支架截面后,得到各种受力条件下波形钢腹板支架比矿用工字钢支架承载力的提高程度。表2则给出了按照相同承载力的条件反算波形钢腹板支架比矿用工字钢支架节省的用钢量大小。从表1 和表2 可以看出,波形钢腹板支架比矿用工字钢支架承载力提高1 倍以上,用钢量也明显小于矿用工字钢支架。综合大量计算分析对比表明:相同用钢量情况下,波形钢腹板工型构件比矿用工字钢支架的轴压承载力可提高10%～20%,弯曲、压弯承载力最大可分别提高约80%和169% ;在承载力一定的情况下,轴心受压时,采用波形钢腹板构件用钢量可节省5%～13%,纯弯和压弯时,波形钢腹板构件节省用钢量最大可达30% 和44%,具有良好的经济效益。

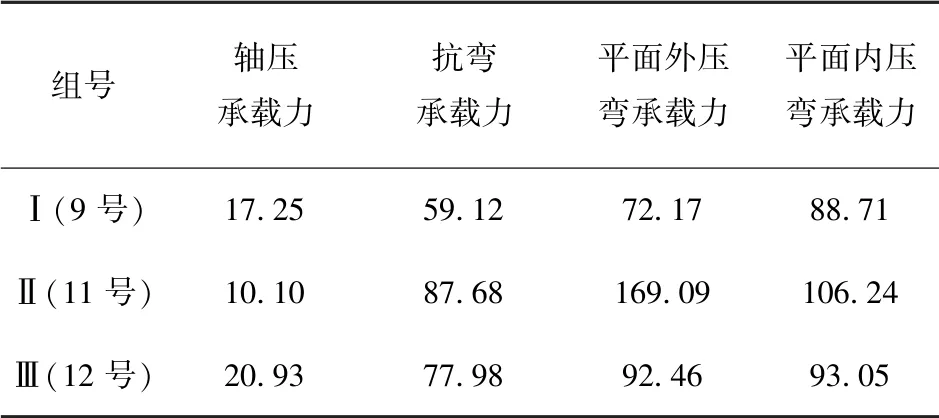
表1 波形钢腹板构件比矿用工字钢承载力提高程度Tab.1 Enhancement degree of bearing capacity of corrugated steel webs compared with mine I-beams %

表2 波形钢腹板构件比矿用工字钢用钢量节省程度Tab.2 Saving degree of corrugated steel webs compared with mine I-beams %

2 波形钢腹板支架整体稳定承载性能研究

2.1 多种断面支架整体稳定承载性能试验

以12 号矿用工字钢支架为基准,设计了1 榀几何缩尺比例为1∶2 的马蹄形支架试验模型[39][图2(a)](跨度L=6 m,高度H=4.75 m),3 榀原型尺寸的圆形断面[40-41][图2(b)](半径为2.6 m,支架的腹板高度为240～300 mm)以及2 榀直墙半圆拱断面的波形钢腹板支架[42][图2(c)](圆弧部分半径为2.6 m,直腿部分长1.65 m,支架的翼缘厚度变化范围为12～16 mm)进行稳定承载力模型试验,并同时加工了1 榀相同用钢量圆形断面的矿用工字钢支架试验模型[图2(d)]与波形钢腹板支架进行对比。

图2 各种断面形式支架的模型试验Fig.2 Model test of supports with various cross-section

试验结果表明,马蹄形断面波形钢腹板支架稳定承载力是相同用钢量矿用工字钢的2 倍,位移仅为后者的1/3。圆形断面和直墙半圆拱断面的波形钢腹板支架稳定承载力约为相同用钢量矿用工字钢支架的1.3～1.5 倍,最大位移仅为后者的70%～80%,整体稳定性能显著优于矿用工字钢。

将试验结果与有限元模型进行了对比,如图3所示。图3(a)中,马蹄形断面支架的有限元计算(FEA)和模型试验结果仅相差1.4%,极限状态时拱顶竖向位移相差15%。图3(b)中,圆形断面支架的有限元和试验承载力结果相差2.71%,拱顶竖向位移相差7.12%。图3(c)中,直墙半圆拱支架的有限元和试验结果仅相差6.7%,拱顶竖向位移也仅相差15.71%。对比结果验证了波形钢腹板支架有限元模型的正确性。

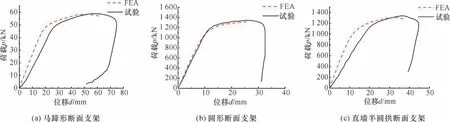
图3 不同断面形式支架的试验结果与有限元分析对比Fig.3 Comparison of the experimental results and the finite element analysis of the support with various cross-section forms

表3 为相同用钢量下圆形断面波形钢腹板支架与12 号矿用工字钢支架的对比情况。波形钢腹板支架YX-1 比矿用工字钢支架KY-1 的极限承载力提高了46.82%,其单位重量承载能力为矿用工字钢的1.49 倍,且最大位移仅为矿用工字钢的74%。

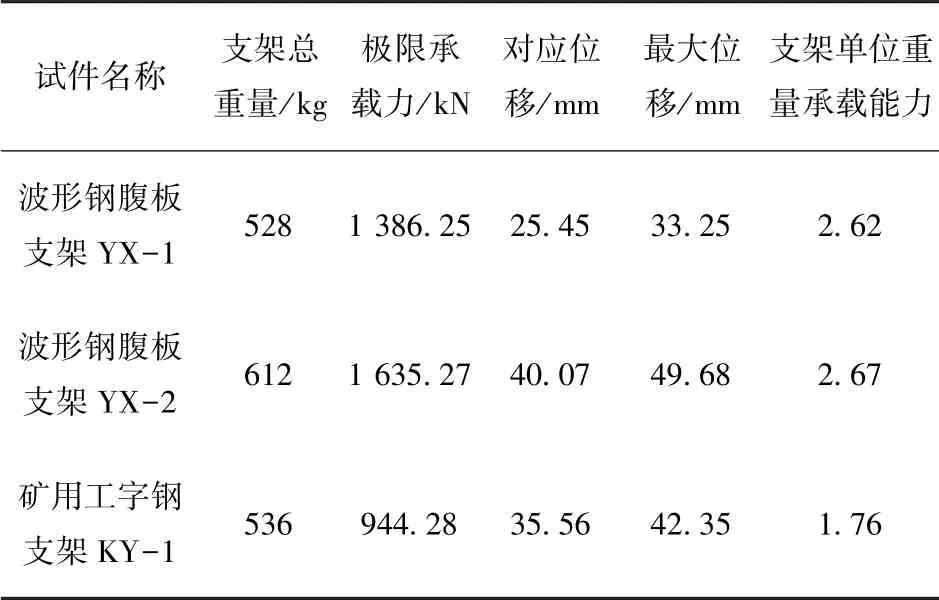
表3 圆形断面支架的承载能力对比Tab.3 Comparison of carrying capacity of steel circular closed supports

2.2 有限元参数分析

采用ANSYS 软件对各种形状的波形钢腹板支架进行了弹性和弹塑性屈曲的参数分析[40-45],研究随着波形钢腹板的高度hw、厚度tw、波幅f、波长λ,翼缘的宽度bf、厚度tf等参数的变化,支架结构的弹性和弹塑性屈曲荷载的变化情况及其分析结果如图4、图5所示。总体上,对于3 种断面波形钢腹板支架,腹板高度、翼缘宽度和厚度对各支架的弹性稳定承载力影响较大。腹板高度、翼缘宽度和厚度对于圆形断面支架弹塑性稳定承载力影响较大;腹板高度和厚度对于直墙半圆拱支架弹塑性稳定承载力影响较大;腹板高度、腹板厚度对马蹄形支架弹塑性稳定承载力影响较大。

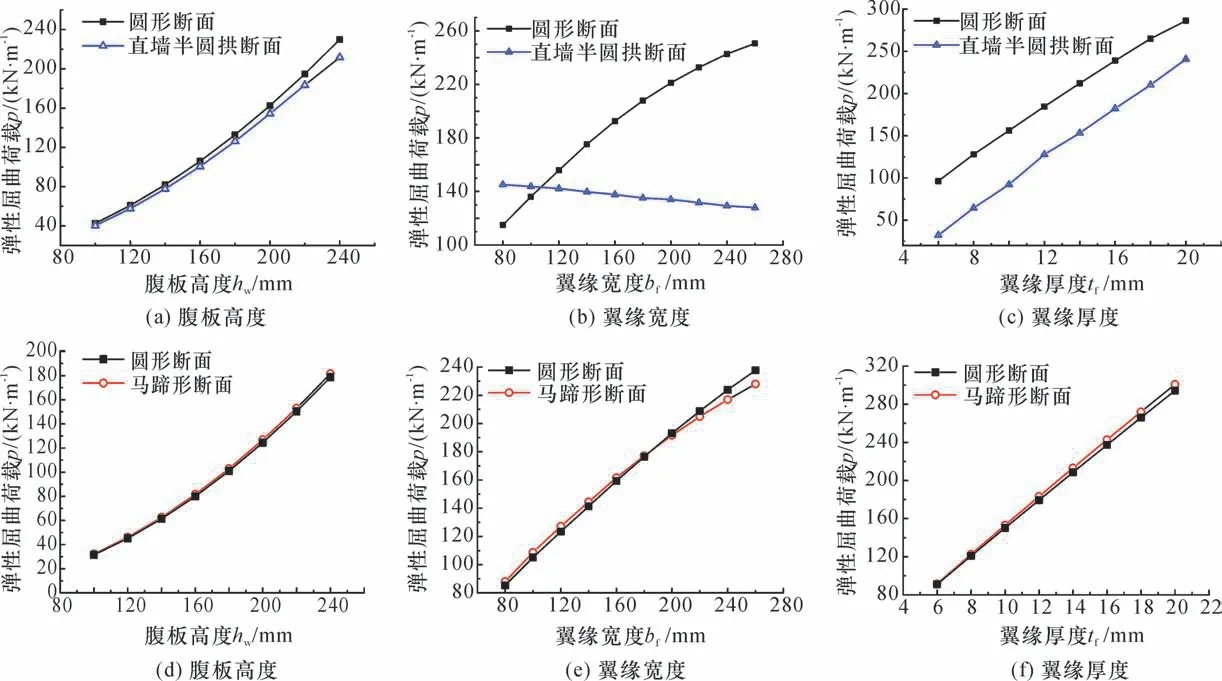
图4 支架弹性屈曲荷载与各参数的关系曲线Fig.4 Relations between the elastic buckling load of support and various parameters

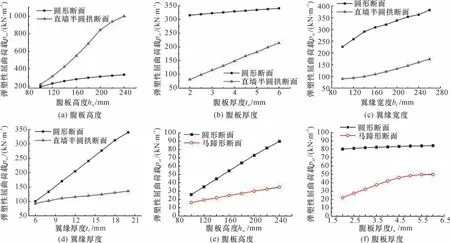
图5 支架弹塑性屈曲荷载与各参数变化的关系曲线Fig.5 Relations between elastoplastic buckling load of support and various parameters

2.3 支架平面内整体稳定承载力设计方法

基于有限元参数分析,采用正交设计方法计算[41],得到了纯压支架平面内的稳定设计曲线(图6),为方便设计人员使用,给出了不同长细比下的稳定系数计算表格(表4)。我国现行钢结构设计标准[45]中规定,对焊接工字型截面采用b 类稳定设计曲线,而从图6 中可以看出,当长细比小于60时,纯压支架的稳定系数低于规范值;而当长细比大于60 时,纯压支架的稳定系数又高于规范值。纯压支架的稳定曲线与轴心受压直构件的稳定曲线有较大出入,这表明不能参照直构件的稳定设计曲线进行设计。因此,结合《波浪腹板钢结构应用技术规程》[46]中的波浪腹板工形轴压直构件平面内稳定承载力设计方法,提出波形钢腹板纯压支架平面内稳定承载力的设计公式[41]如下:

图6 波形钢腹板纯压支架稳定曲线与《钢结构设计标准》的对比Fig.6 Comparison of stability curve between the calculated result and the curve in specification for design of steel structures

式中,N为支架的轴力设计值,采用一阶线弹性计算结果;A为支架的毛截面面积;f为钢材强度设计值;φ为弯矩作用平面内的纯压支架的稳定系数,应根据波形钢腹板构件绕强轴的等效长细比λ0x查表4 得到。

表4 波形钢腹板支架稳定系数Tab.4 Stability coefficient of steel supports with corrugated webs

构件绕强轴的等效长细比λ0x按下列公式进行计算:

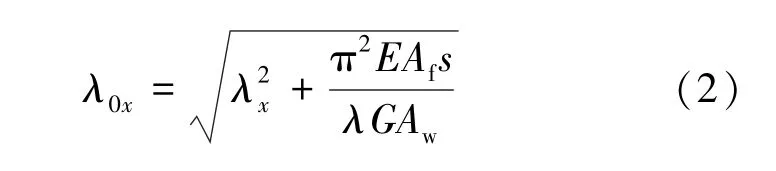
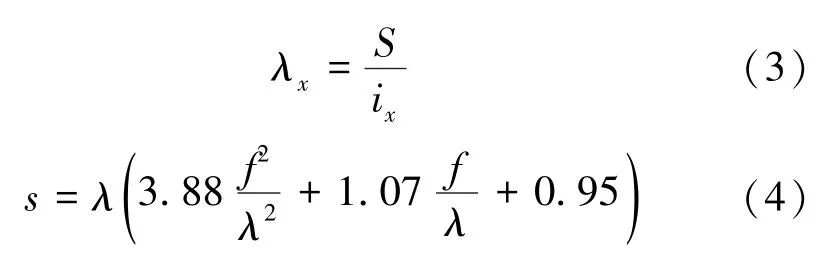
式中,λ为波浪腹板一个波浪的波长;s为波浪腹板一个波浪展开后的长度;f为波浪腹板波幅;S为封闭支架的计算弧长度;Aw为腹板截面面积。

同时,综合《波浪腹板钢结构应用技术规程》[46]和《拱形钢结构技术规程》[47]提出了波形钢腹板压弯支架平面内稳定承载力的建议设计公式:

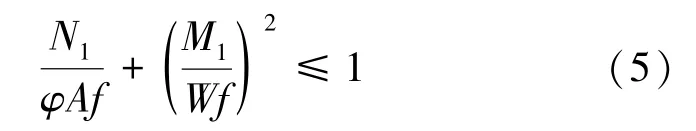
式中,N1为设计最大轴力;M1为设计最大弯矩;W为对较大纤维的毛截面模量(弯矩作用平面内)。

3 波形钢腹板支架结构局部稳定性能的研究进展

3.1 支架局部稳定性能的试验研究

钢结构的局部失稳有时并不会导致结构立刻失效,但一旦局部失稳(屈曲),必然会影响到结构的整体稳定行为。为了深入研究波形钢腹板支架板件局部屈曲性能,开展了6 榀半圆拱形支架的局部稳定性能试验,并分别探究其在均布加载以及多点加载下的局部失稳形态及内力的变化规律[48]。仍以12 号矿用工字钢支架为基准设计波形钢腹板支架,分别设计了2 组试验,每组各3 榀半圆弧拱,分别研究翼缘和腹板的局部失稳问题。翼缘局部失稳组系列中的翼缘厚度分别为4 mm、6 mm和8 mm,其他参数相同,主要分析翼缘厚度对翼缘局部稳定的影响。结果表明,达到极限荷载时,支架的翼缘呈现了较明显的向内凹陷或向外鼓曲现象,如图7所示;翼缘的厚度(宽厚比)越大,翼缘的局部稳定性能越好,极限承载力越高。当波形钢腹板支架的翼缘厚度由4 mm 增加至6 mm 及8 mm 时,其失稳荷载从277.6 kN 增加至857.68 kN 及1 443.23 kN,相邻增幅分别是209% 、68%。可见,翼缘厚度是影响局部稳定承载力的主要因素。

图7 波形钢腹板支架翼缘发生局部失稳Fig.7 Local instability of flange of support with corrugated webs

腹板局部失稳组中腹板高度分别为200 mm、300 mm 和400 mm,其他参数相同。结果表明,极限荷载时,支架腹板发生明显的局部失稳,腹板被压屈,加载杆随着垫块将翼缘顶至凹陷,从而带动构件的整体失稳,如图8所示。腹板的高度(高厚比)越大,腹板的局部稳定性能越好。当波形钢腹板支架的腹板高度由200 mm 增加至300 mm 及400 mm 时,其失稳荷载从1 273.22 kN 增加至1 390.76 kN 及1 475.52 kN,相邻增幅分别是9% 、7%。可见,腹板高度对支架局部稳定承载力具有一定影响,但不及翼缘厚度。

图8 波形钢腹板支架腹板发生局部失稳Fig.8 Local instability of web of support with corrugated webs

3.2 支架局部稳定性能的数值分析

通过局部稳定性能试验,本研究得到了支架的局部屈曲特性和重要影响参数,并验证了有限元模型的正确性[48]。改变支架截面高厚比(hw/tw)、宽厚比(bf/tf)以及圆心角(矢跨比)等参数,对波形钢腹板拱结构进行了弹性和弹塑性局部稳定的参数化分析[48],部分分析结果见图9。结果表明,翼缘宽度bf和厚度tf,腹板高度hw和厚度tw均对支架局部稳定性能的影响较大,增大翼缘宽度和厚度可提高翼缘的局部极限承载力;适当增大腹板高度和厚度,翼缘宽度和厚度均可提高腹板的局部稳定承载力。随着圆心角的增大,翼缘局部稳定承载力逐渐减小;圆心角对腹板局部稳定承载力影响较小。

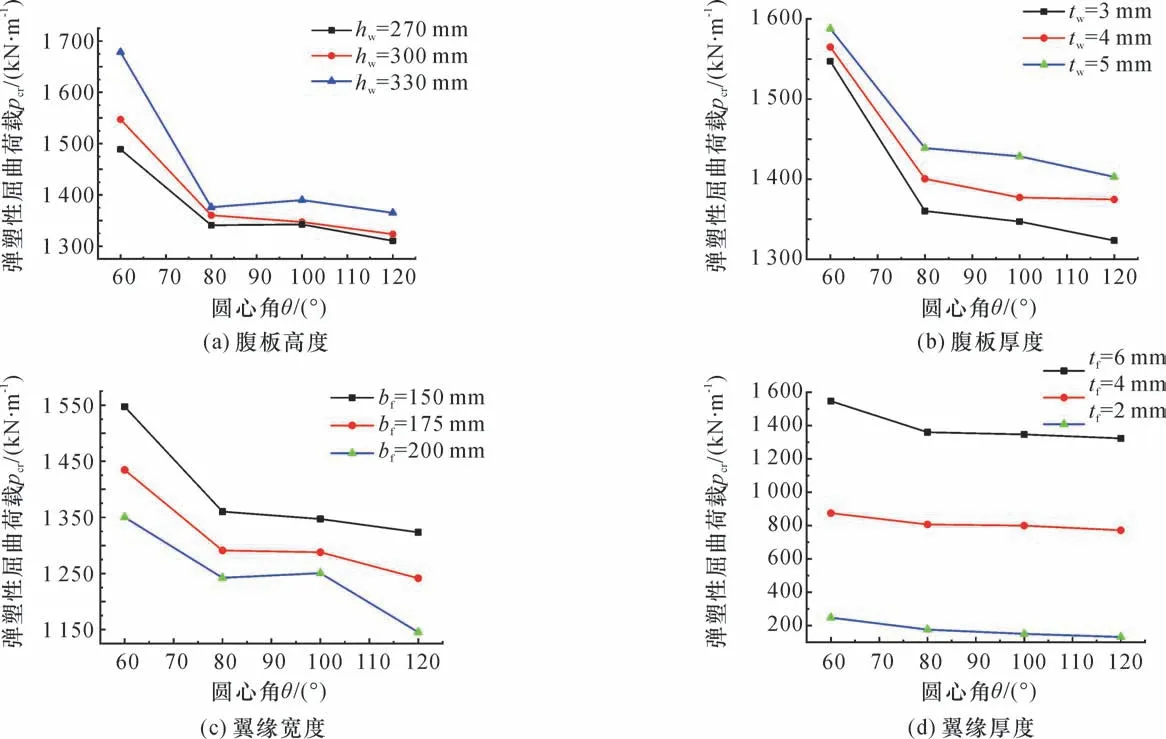
图9 支架弹塑性局部屈曲荷载与各参数变化的关系曲线Fig.9 Relations between the local elastoplastic buckling load of support and various parameters

4 波形钢腹板支架可缩性节点的研究进展

波形钢腹板支架的腹板为波浪形,可以利用这种特有构造适应巷道围岩大变形。为此,研发了2大类波形钢腹板支架可缩性节点构造,即高强度螺栓连接节点和楔形件套筒连接(图10),并同时设计了7 个可缩性节点试验构件[49],包括6 个高强螺栓连接可缩性节点试件和1 个楔形件套筒可缩性节点试件。

图10 两类可缩性节点试验装置图Fig.10 Schematic diagram of instruments for two types of yieldable joint

以国内某工程为背景设计了马蹄形断面支架,其中各节点可缩量为160 mm。结果表明,该可缩性节点构造可以实现滑动,且在滑动过程中能维持一定的摩擦力。由此可见,该类型可缩性节点能基本适应软岩变形而发生轴向变形。套筒可缩性节点轴压试验结果也表明,该可缩性节点也可以实现滑动,但滑动摩擦力很大程度上取决于摩擦面的处理和楔子与构件之间的预紧力。针对研究结果,提出了今后开展节点设计的改进方案,如由双排双列螺栓改为双排三列;由盖板、翼缘同时开孔改为只在连接盖板上开椭圆形长孔,翼缘上只开螺栓直径大小的孔;在横向加劲肋的基础上,增加纵向加劲肋,以增加局部的刚度;加大楔形件的坡度或增大摩擦面粗糙度来增大摩擦力等。

根据支架节点需满足的可缩量采取不同的可缩方案:

(1)当可缩量较小(＜100 mm)时,结合应用抗爆缓冲材料或吸能材料与波形钢腹板支架形成吸能支护体系。不设置可缩性节点,先依靠吸能材料变形适应围岩变形,基本稳定后依靠波形钢腹板支架承受围岩荷载。

(2)当可缩量中等(100～200 mm)时,可用高强度螺栓连接可缩性节点,可缩量通过翼缘和盖板的开孔长度来实现,这种节点对施工质量要求较高,后续对本文设计的节点再继续优化改进。

(3)当可缩量较大(＞200 mm),可采用套筒连接的可缩性支架。此种支架节点刚度大、承载力较高,设计和加工较简单。

5 软岩巷道波形钢腹板支架与围岩相互作用关系研究

采用ANSYS 和FLAC3D有限元软件分析了3种地质条件下,波形钢腹板支架与围岩的相互作用问题[50]。3 种地质条件和工程背景如下:

(1)国内某单一岩性围岩煤矿巷道。其巷道处于-350 m 水平,巷道半径2.5 m,煤种为褐煤及长焰煤,页岩含油率14.31%。井田地质构造及水文情况简单,硐室围岩岩性比较单一,主要是含油泥岩,岩石强度低。

(2)根据山东省龙口市北皂煤矿中海域二采区巷道模拟极软岩层。所采煤层厚度为3.51～8.87 m。煤层顶部为灰褐色泥岩、含油泥岩、页岩,具有水平层理,局部夹薄层为泥灰岩,含油泥岩上部渐变过渡为棕褐色页岩,水平层理发育。

(3)根据河南省的陈四楼煤矿巷道模拟高应力软岩。巷道埋深为-430 m,有断层穿过,周边围岩多为软弱的破碎岩石,巷道周边受构造应力的影响较大,煤矿周边地质条件差,受力复杂,周围岩性差,自承载能力低。

计算结果表明,采用波形钢腹板联合支护后,单一岩性圆形巷道顶、底板的缩进量相对原结构位移减小量超过了400 mm,巷道断面两帮收缩量比原结构减少了500 mm;极地软岩复杂岩性巷道在垂直方向的缩进量相对原结构位移减小了400 mm,两帮总缩进量相对于原支护结构减少了约900 mm;高应力围岩复杂岩性巷道顶、底板的缩进量相对原结构位移减小了400 mm,巷道断面两帮收缩量相对于原结构减少了500 mm。采用波形钢腹板支架后,3 种地质条件下巷道顶、底板和两帮的主要位移均比仅采用锚杆支护的结果明显减小。考虑波形钢支架与围岩相互作用与不考虑相互作用两种情况下,支架的内力发展趋势相近,但不考虑相互作用时支架内力大于考虑两者相互作用时的受力(图11 为极软地层围岩条件下的分析结果)。这是因为考虑相互作用后,围岩与支架之间产生相互作用,共同应对应力重分布影响,故内力相对不考虑的情况小。

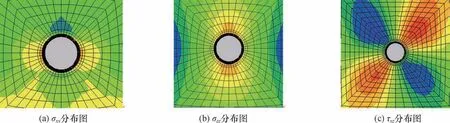
图11 极软地层围岩波形钢腹板联合支护体系下围岩的应力分布Fig.11 Stress distribution diagram of surrounding rock under the combined support system of corrugated webs in extremely soft strata

6 结论

(1)相同用钢量条件下,波形钢支架承载力是矿用工字钢的1.5～2.5 倍,变形量降低30%～60% ;相同承载力条件下,用钢量减少20%～45%。波形钢腹板支架可节约资源,实现矿山资源的绿色高效开采,巷道服务期满还可拆卸,重复利用,绿色环保。

(2)基于多种巷道断面波形钢腹板支架整体稳定和局部稳定承载性能的试验研究、数值计算和理论分析,给出了纯压和压弯受力状态下波形钢腹板支架的承载力设计公式,为实际工程设计提供了参考。

(3)针对巷道围岩大变形问题,研发出了高强度螺栓和楔形件套筒两类可缩连接节点构造,解决了传统可缩构件的偏心受力问题。通过可缩卸压降低了作用在支架上的围岩荷载,提高了波形钢腹板支架支护结构的稳定性和服务周期。

波形钢腹板支架属于高强轻质支护材料,它的使用不仅提高了深部巷道支护强度,而且通过结构优化,节省了大量钢材,减少了支架重量,降低了井下工人施工劳动强度。

结合波形钢腹板支架可缩、让压的特性,在已有研究成果的基础上,未来应进一步开发新型抗冲击地压复合支架吸能支护体系,实现“以柔克刚、刚柔结合、缓冲让压、稳定支护”的核心目标,使之具有两级吸能防冲机制,有效保证冲击地压下能量的快速耗散,为突破目前抗冲击地压尚缺乏高效防冲支护结构这一技术瓶颈提供有益参考。