相邻巷道围岩动态裂纹起裂与扩展行为研究

杨立云张飞陈思羽胡桓宁汪自扬林长宇

中国矿业大学(北京)力学与建筑工程学院,北京 100083

在巷道、隧道建设工程中,经常会在自然岩体中开凿硐室通道,此时围岩的安全稳定问题尤为重要。巷道周边岩体的失稳破坏往往由应力集中导致初始微观裂纹引起,伴随着应力重分布、能量集聚等复杂耦合作用,微观裂纹进一步扩展,最终演化为宏观的岩体破坏。尤其是当岩体受到冲击、爆炸等强动荷载作用时,这种破坏会给工程建设带来不可忽视的严重后果。

巷道周边岩体动态裂纹扩展问题引起了国内外众多学者的关注,并开展了一系列有益工作。周磊等[1-3]对巷道内动态裂纹的起裂及扩展特性、内在机理等进行了实验研究,结果表明巷道内岩体裂纹的起裂扩展特性与荷载类别、角度、加载率等因素有密切的联系,厘清了巷道内动态裂纹扩展规律。王蒙等[4-5]借助分离式霍普金森压杆(Split Hopkinson Pressure Bar,SHPB)实验平台,以巷道岩体裂纹扩展问题为背景,对复合裂纹的扩展规律进行了研究。杨仁树等[6-8]利用焦散线原理,对裂纹扩展特性开展了类岩石介质模型实验研究,详细分析了在冲击荷载作用时,动静裂纹的相互影响规律以及缺陷对裂纹扩展特性的影响,为实际工程中岩石动态裂纹扩展提供了一定的理论参考。杨立云等[9]借助焦散线实验系统,研究了双裂纹扩展行为特性受偏置裂纹的影响情况,并对断裂参数变化情况进行总结。许鹏等[10]对含垂直层理介质的爆生裂纹扩展行为特性进行了研究,通过焦散线实验分析了爆生裂纹的扩展规律、动态断裂特性。郭东明等[11]对邻近硐室周边围岩爆炸荷载下初始裂纹的扩展机理进行了实验研究,并结合数值模拟分析了周边岩体的应力分布特征。李清等[12]借助落锤加载实验系统对含偏置裂纹试件开展了冲击加载实验,对动态裂纹起裂、扩展的行为特性进行了分析。Xu 等[13]对隧道裂纹的动态扩展进行了数值模拟研究,结果表明裂纹位置和角度对动态裂纹扩展的影响较为显著,这和周磊等[1-3]人的研究结果较为符合。Wei 和Huang 等[14-15]对岩体裂纹扩展开展了模型实验研究,对岩体内部损伤情况、裂纹扩展特性等岩体破坏特征进行了分析。Zhao 和Han 等[16-17]基于霍姆奎斯特-约翰逊-库克损伤模型(Holmquist-Johnson-Cook damage model,HJC),使用通用粒子动力学(General Particle Dynamics,GPD)代码对高地壳应力的深部隧道中的岩爆进行了研究,通过对动态开挖扰动数值模拟,分析了深部隧道围岩的裂纹萌生、扩展破坏和动力破坏,对深入认识围岩破坏机理提供了重要的参考。

上述关于巷道周边岩体裂纹动态扩展问题的研究尚处于探索阶段,未形成成熟的理论体系。在工程实践中,巷道并不是单一几何断面,在巷道交叉位置、连拱截面等情况下,相邻截面周边岩体裂纹的起裂、扩展情况更为复杂,并且一旦遭受冲击荷载(爆破、岩爆等)往往会发生严重的事故,造成不可挽回的损失。为了研究相邻巷道周边围岩在冲击荷载下动态裂纹起裂、扩展的力学行为特性,本文借助新型数字激光动态焦散线实验系统[18]进行了双截面巷道模型冲击实验,从裂纹扩展轨迹、动态焦散斑演化过程、动态应力强度因子变化、裂纹扩展运动学特征等角度对裂纹起裂、扩展特性进行分析,并结合应力波传播特性和动态裂纹扩展数值模拟,厘清相互影响规律,旨在为实际工程相邻巷道周边岩体动态起裂破坏提供一定的参考。

1 实验原理

1.1 焦散线原理

焦散线是利用光线照射到结构受力的奇异区上,在成像屏上产生相应的焦散线来分析奇异特征参量的方法。该方法只需测量焦散斑直径就可以确定裂纹尖端的应力强度因子,具有较高的测量精度[18]。

应力集中区域I 型裂纹的光线分布如图1所示。靠近裂纹尖端的区域,光线通过时的偏转角度大,因此焦散图像上四周亮区与中心暗斑之间有一条很明显的边界线,这两个区域间的边界线称为焦散线,暗影区称为焦散斑。

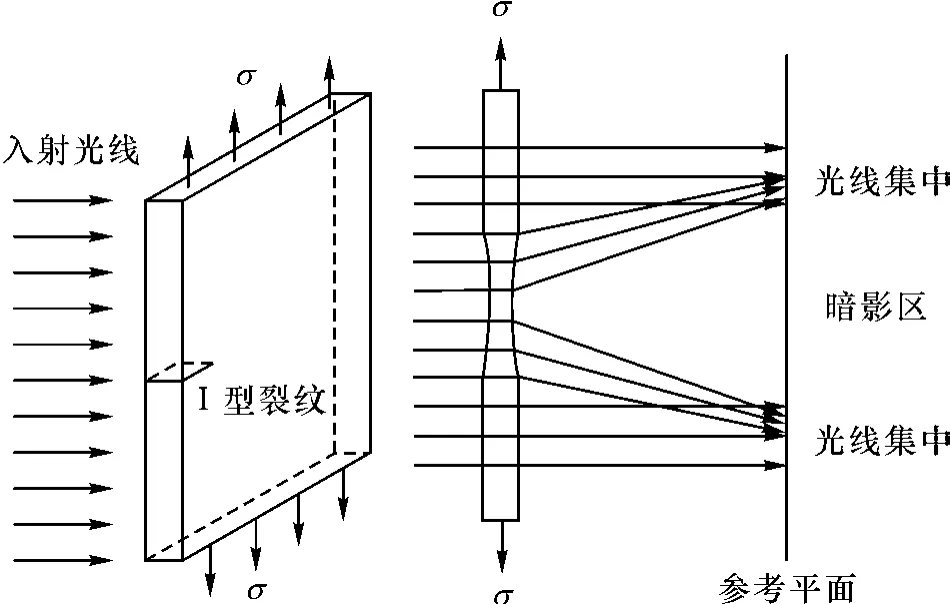
图1 应力集中区域光线分布示意图Fig.1 Schematic diagram of light distribution in stress concentration area

光线偏转的映射关系如图2所示,对光线定量分析[18]可以得到

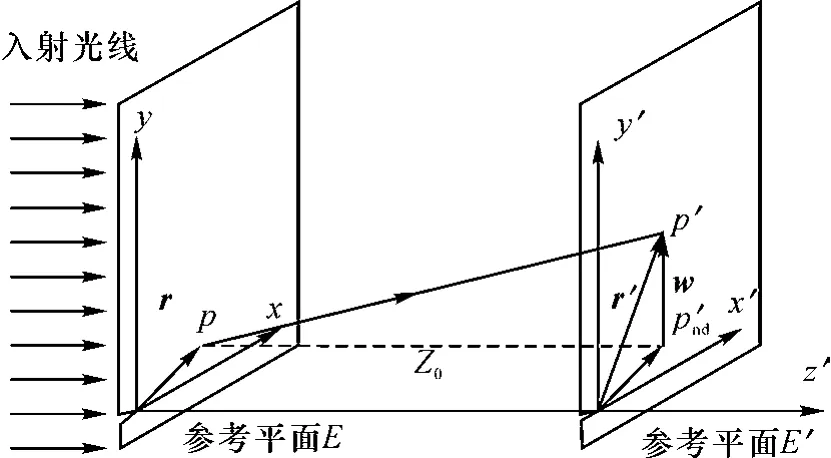
图2 光线映射关系示意图Fig.2 Schematic diagram of light mapping relationship

式中,r′、r、w为裂纹尖端一点的向量;Z0为试件至参考平面距离;Δs为光程差。

把裂纹尖端的应力分布式、光程差与应力光学定律[18]代入式(1),可得映射方程:

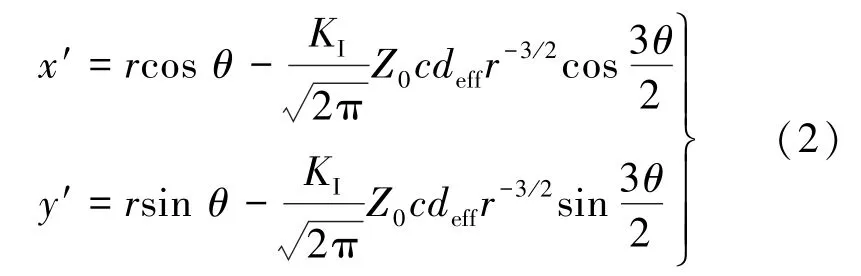
式中,r、θ为裂纹尖端点极坐标;deff为试件有效厚度;c为材料焦散光学常数;KⅠ为Ⅰ型裂纹尖端应力强度因子。

假设试件介质各向同性,由光学原理可知焦散线是一条奇异曲线,因此有

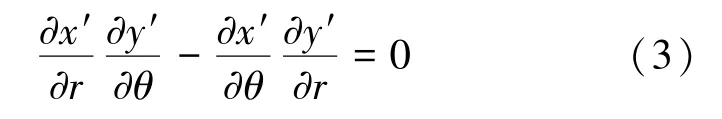
可得焦散线方程表达式:

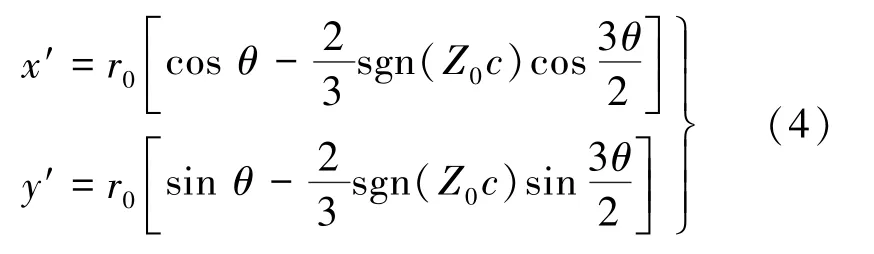
式中,r0为初始曲线半径。

定义焦散斑直径最大值Dmax为其特征尺寸,可得

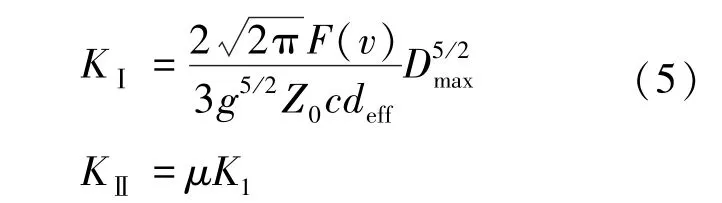
式中,F(v)为速度修正因子,在具有实际意义的扩展速度时,可近似取1;Dmax为焦散斑直径最大值;g为数值因子,取3.17;Z0取900 mm;μ为应力强度因子比例系数。

1.2 实验系统

新型数字激光动态焦散线实验系统如图3所示。该系统包括光路和数据记录两部分,主要由激光器、扩束镜、场镜、高速相机、计算机、同步控制开关组成。试件受荷载作用时,高速相机和计算机通过信号触发实现同步工作,试件产生的焦散斑图像被计算机记录。实验系统的工作原理如下:落锤释放加载,产生断-通信号,经导线控制器输入相机外部接口,触发相机开始拍摄图像。激光光源为绿色固体激光器,高速相机为Fastcam-SA5(16 G)型彩色数码相机,设置相机拍摄帧率150 000 fps,分辨率72 ppi,拍摄区域大小为128 pixels×184 pixels,快门速度1/250 000 s。

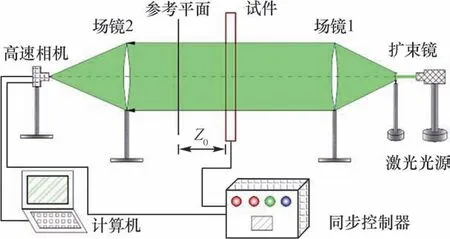
图3 新型数字激光动态焦散线实验系统Fig.3 New digital laser dynamic caustics experimental system

2 实验过程

2.1 模型制作

根据相似模拟理论,试件按照1∶500 比例进行设计,试件示意图如图4所示。

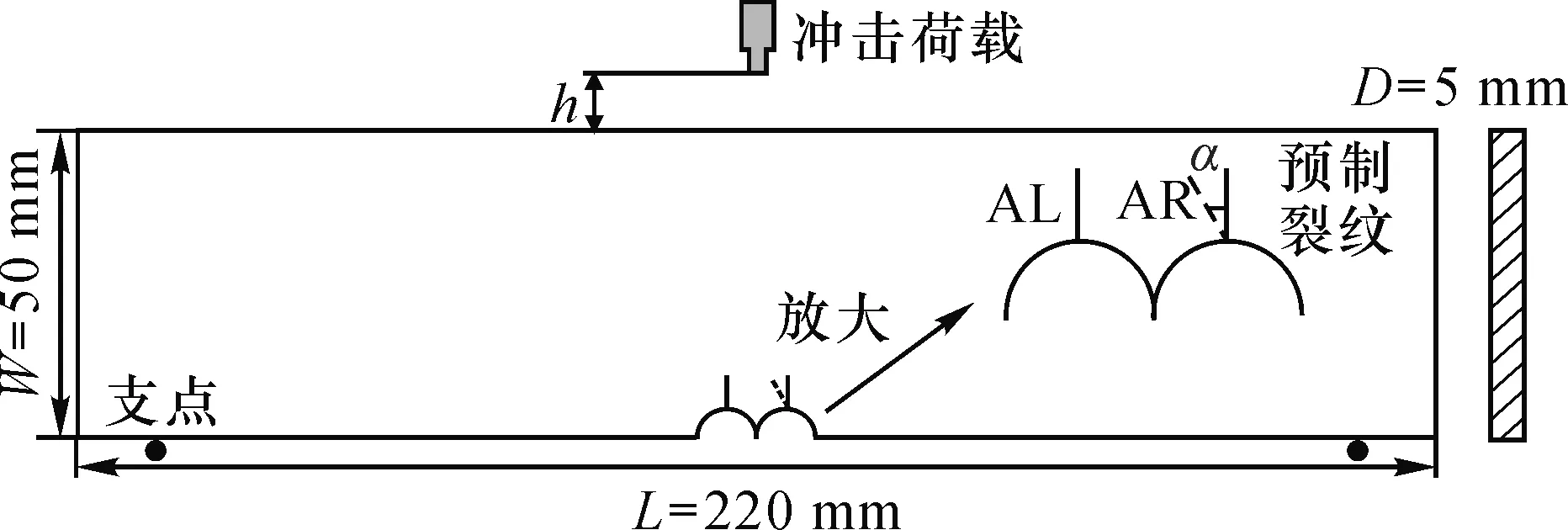
图4 试件示意图Fig.4 Schematic diagram of specimen

试件下部设计2 个相邻半圆拱截面用以模拟实际工程中的两相邻半圆拱巷道,其半径为5 mm;试件尺寸长(L)×宽(W)×厚(D)为220 mm×50 mm×5 mm;落锤冲击高度h为300 mm。圆弧顶部预制0.5 mm×5 mm 竖向裂纹,其中右侧预制裂纹与竖直方向的偏转夹角α为控制变量;记逆时针偏转为正,α分别为45°、22.5°、0°、-22.5°、-45°;α为45°的试件编号记为试件SA,左侧裂纹记为AL,右侧裂纹记为AR,其他试件依次编号。试件加工采用激光切割工艺,试件材料为有机玻璃(Polymethyl Methacrylate,PMMA),透光性强,力学特性和岩石相似,能理想地用来模拟岩石介质裂纹扩展等动态力学行为[6-8,19-22],其物理性能参数如下:密度ρ=1 200 kg/m3,弹性模量Ed=6.1 GPa,泊松比υ=0.32,动态抗拉强度σt=30 MPa,纵波波速cp=2 320 m/s,横波波速cs=1 260 m/s,光学常数c=-1.08×10-10m2/N。

2.2 冲击荷载加载

落锤从高度300 mm 处释放,落锤质量1.5 kg,落锤冲击与试件接触的锤头产生冲击荷载,作用在试件顶部中间位置;同时,高速相机同步记录图像信息。记落锤锤头接触试件的时刻为0 μs。以锤头作用点为中心,试件瞬间承受冲击荷载作用后,产生应力波向下方传播,经过约40 μs 后波锋面到达下部预制裂纹尖端。

3 实验结果与分析

3.1 试件断裂结果

试件在冲击荷载作用下均发生断裂破坏,试件中间部分断裂效果如图5所示。可以发现,在冲击荷载作用下,试件从预制的竖向裂纹尖端处起裂扩展进而断裂及破坏,并且裂纹扩展轨迹有“径直”向上延伸的趋势。

图5 试件断裂效果Fig.5 Fracture effect diagram of specimen

通过计算试件裂纹扩展轨迹的曲折度,可以定量评价扩展轨迹特征。曲折度为裂纹轨迹长度(Lt)与裂纹起点到终点的直线距离(L0)之比。由表1 计算结果可知,裂纹扩展轨迹曲折度均在1.0 左右。

表1 裂纹扩展轨迹曲折度Tab.1 Crack propagation path tortuosity

3.2 焦散斑演化过程分析

试件SA至SE的裂纹尖端焦散斑变化情况如图6所示。限于篇幅,以试件SA为例介绍。当t=0 μs时,开始冲击加载,约40 μs 后,可以观察到左侧预制裂纹AL 尖端处焦散斑开始明显增大,应力开始在此集中,应力波携带的能量集聚。当t= 140 μs时,焦散斑直径增加到最大,随后,裂纹起裂扩展,在扩展过程中,裂纹尖端的焦散斑持续存在,说明应力波携带的能量一直驱动裂纹扩展。当t=273 μs 时,裂纹尖端邻近试件顶部,此后,焦散斑快速减小,试件完全断裂。右侧预制裂纹AR 尖端处焦散斑在140 μs之前也有增大过程,但比AL 的小,在AR 起裂后,快速减小并消失在相机视野中。

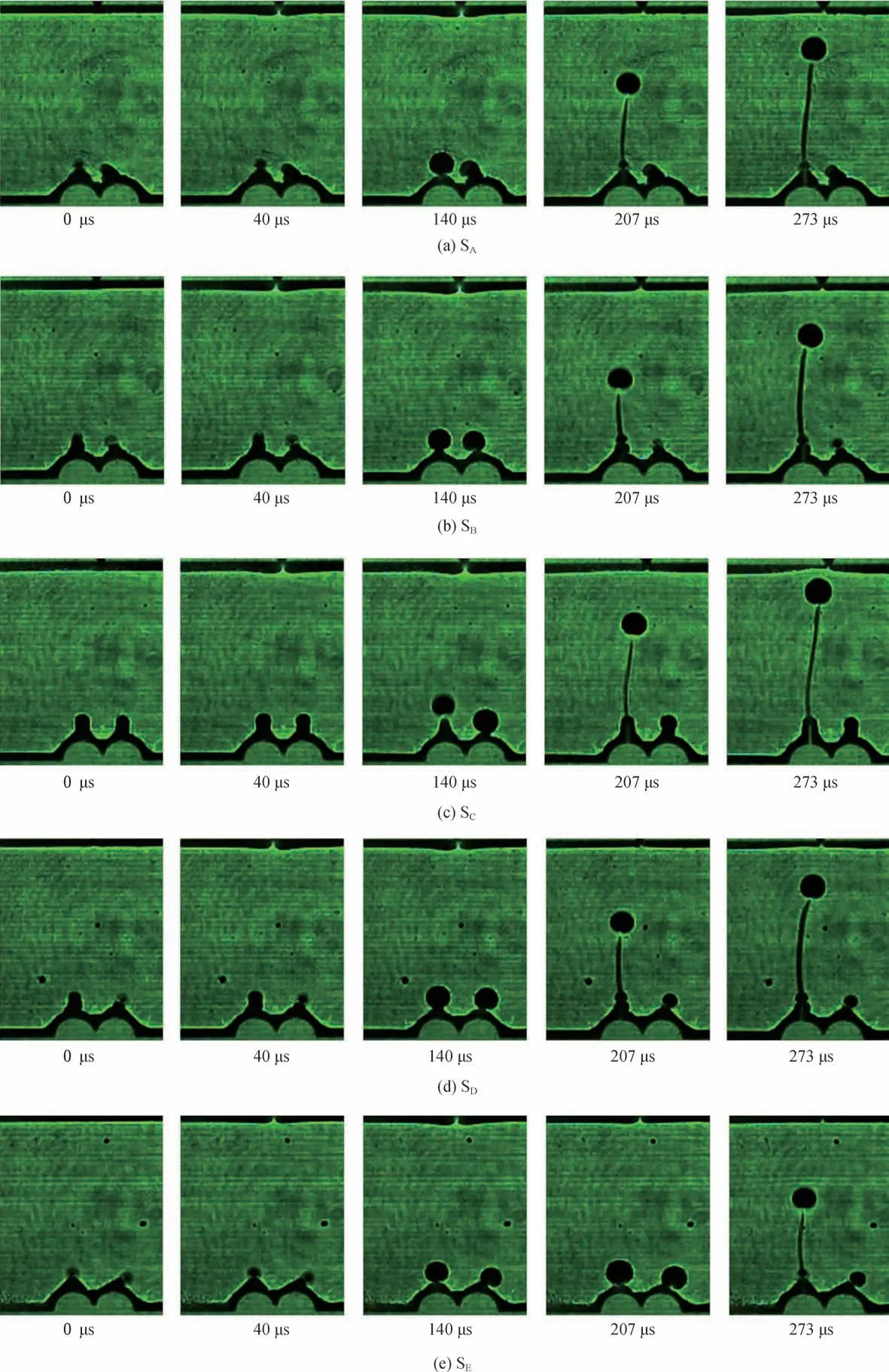
图6 裂纹尖端焦散斑Fig.6 Caustic speckle at crack tip

比较左右两侧焦散斑的几何特征发现,左侧焦散斑为轴对称图形(Ⅰ型焦散斑为主),这是因为应力波到达裂纹AL 尖端后,在张拉力主导作用下,裂纹尖端产生以Ⅰ型为主的裂纹;右侧裂纹AR 偏转一定角度,同时承受张拉力和剪切力两者耦合作用,产生Ⅰ、Ⅱ复合型裂纹,焦散斑为旋涡状。由于落锤每次从同一高度释放,产生的应力波强度相同,因此在试件内部的能量场总量是一样的。当应力波波锋面到达左右预制裂纹尖端时,应力开始在此集中,能量集聚;右侧裂纹AR 分得一部分能量后,如果驱动裂纹起裂,就要同时克服上述的复杂耦合力场作用;在此过程中,能量耗散,难以起裂,实验结果也验证了这种观点。当α为45°、22.5°、-22.5°、-45°时,试件从左侧裂纹尖端处起裂、扩展、断裂;α为0°时,也即左右两个裂纹都在竖直方向时,试件起裂位置有一定的随机性,两侧都可能起裂,说明在能量聚集过程中,先达到起裂韧度的一侧会率先起裂。

3.3 动态应力强度因子的变化

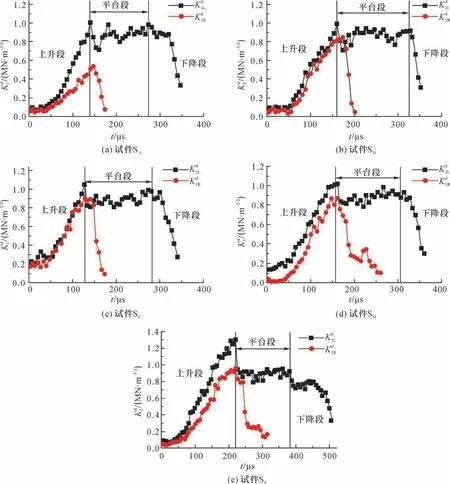
图7 不同试件动态应力强度因子变化Fig.7 Change of dynamic stress intensity factor

图7(a)中,试件SA左侧裂纹AL 尖端的动态应力强度因子在t=50 μs 后开始明显增大;当t=140 μs 时,为1.01 MN/m3/2,此时裂纹起裂;随后进入一个平台段,持续时间约160 μs,在此阶段裂纹持续扩展;约t=300 μs 时,开始快速下降。在一些学者[23-24]的相关实验中,同样有裂纹起裂后,应力强度因子不会大幅下降而是保持一段时间的稳定的现象。在140 μs 之前,试件SA右侧裂纹AR 尖端的应力强度因子的增加趋势和相似,但是没有增加得快;140 μs 后,应力强度因子迅速下降。整个过程右侧裂纹AR并未起裂,这是因为试件SA左侧裂纹AL 的动态应力强度因子在上升段增加得更快,在此集聚的能量更多;起裂扩展后,左侧裂纹尖端的能量场瞬间得以部分释放,形成能量“负压”,右侧裂纹尖端处的能量场向左侧转移,直线下降,右侧裂纹未能起裂。

图7(b)中,试件SB在上升段和的趋势趋同,同样整体高于,说明左侧裂纹尖端处的应力集中程度更大,能量集聚更多,更容易起裂。在t=160 μs 时,为0.99 MN/m3/2,左侧裂纹起裂后,短暂下降后进入一个平台段,持续时间约166 μs,则快速下降;t=320 μs 时,快速下降,裂纹扩展贯通,试件断裂破坏。

图7(c)中,试件SC在上升段,和的趋势在前期相同;t= 100 μs 时,增长大于;t=127 μs 时,为1.05 MN/m3/2,随后左侧裂纹起裂;短暂下降后进入一个平台段,持续时间约166 μs,则快速下降;t=293 μs 时,快速下降,裂纹扩展贯通,试件断裂破坏。

图7(d)中,试件SD在上升段高于,t=120 μs 时,左侧裂纹起裂后,变化和其他试件相似。

图7(e)中,试件SE的变化情况也和其他试件相似,但在上升段比整体增加趋势更快。

图8 应力强度因子和平台段持续时间tcon 的关系Fig.8 The relationship between the stress intensity factor and the plateau duration tcon

3.4 裂纹扩展运动学分析

为进一步分析裂纹动态扩展过程,需从运动学角度分析其规律,图9 为裂纹起裂所需时间和裂纹扩展速度变化情况。

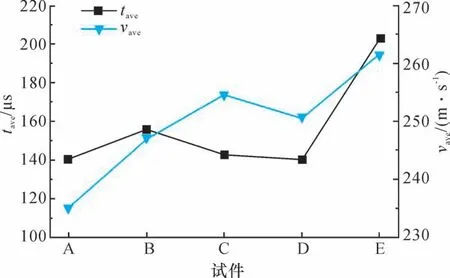
图9 裂纹起裂所需时间和扩展速度Fig.9 Crack initiation time and propagation velocity

裂纹起裂时需要一定的时间集聚能量,当足以驱动裂纹扩展时,从裂纹尖端起裂,进入扩展阶段。随着右侧裂纹向右偏转,也即两相邻截面裂纹尖端愈来愈远,裂纹起裂所需时间有所不同,偏转角度α为45°、22.5°、0°、-22.5°时,试件起裂所需时间平均值tave有小幅变化,但基本保持在140 μs 左右;偏转角度α为-45°时,所需时间为200 μs;当右侧裂纹尖端靠近左侧裂纹尖端时,会分得一部分能量,由3.3 节分析可知,此时左侧截面裂纹容易起裂,所以未能持续较长时间的集聚能量;当右侧裂纹向右偏转时,这种影响不再显著。随着控制变量α由45°向-45°变化,也即右侧截面裂纹向右偏转逐渐远离左侧截面时,左侧裂纹起裂后的扩展速度呈现上升的趋势,速度平均值vave分别为235 m/s、247 m/s、255 m/s、251 m/s、262 m/s;结合前文分析可知,由于右侧截面裂纹靠近左侧截面裂纹时,左侧裂纹的应力场分布受到干扰,能量场被右侧裂纹分散,因此不仅应力强度因子有所降低,而且裂纹起裂后的扩展速度也不高;当α由正转负,这种干扰效应减弱,扩展速度便呈现上升的趋势。

4 相邻巷道围岩裂纹起裂扩展影响机理分析

4.1 应力波传播特性

试件顶部承受冲击荷载后,以作用点为起始点,产生应力波在试件内部传播。假定试件介质连续均匀,将应力波简化为平面简谐波。应力波的传播如图10所示,应力波对裂纹尖端作用分解如图11所示。

图10 应力波传播示意图Fig.10 Schematic diagram of stress wave propagation

图11 应力波对裂纹尖端作用分解Fig.11 Decomposition of stress wave on crack tip

由应力波的传播特性可知,当其遇到裂纹尖端等缺陷处时会发生反射、绕射,形成正应力和剪应力及其复杂耦合应力场。裂纹尖端应力强度因子达到断裂韧度后,裂纹起裂扩展。也就是说,由于应力波的作用,在裂纹尖端发生应力集中效应,因此可以观察到图6所示的焦散斑现象。巷道周边岩体介质中存在不同几何特征的缺陷,在应力波的作用下容易发生应力集中现象;由于应力场的复杂程度不同,介质发生不同类型的起裂、扩展,从而形成宏观的断裂破坏。

应力波入射到裂纹尖端处,可分解为两个典型的Ⅰ型、Ⅱ型裂纹(对称、反对称),如图11所示。正应力和剪应力可由式(6)和式(7)[25]计算:

式中,θ为y轴方向和波阵面法线方向夹角;σ0为波阵面压力值。

由几何知识可知,左侧巷道截面顶部裂纹,当θ接近90°时,在正应力σθ作用下形成Ⅰ型裂纹,这和3.2 节Ⅰ型焦散斑演化过程分析结果一致。当右侧巷道截面顶部裂纹偏转45°时,θ代入式(6)、式(7)可知,裂纹尖端同时受正应力σθ和剪应力τθ的作用,在两者复杂耦合应力场作用下,形成Ⅰ型和Ⅱ型复合型裂纹。

由式(6)、式(7)可知,正应力σθ、剪应力τθ的大小与θ值大小呈三角函数关系。正应力σθ、剪应力τθ的分解系数变化关系如图12所示。随着偏转角度变化,正应力σθ和剪应力τθ的大小发生改变,因此带来了耦合应力场的复杂变化,对左侧巷道截面顶部裂纹的起裂扩展造成影响。

图12 正应力σθ 和剪应力τθ 分解系数随θ 变化关系Fig.12 The decomposition coefficient of σθ and τθ with θ

4.2 动态裂纹扩展过程数值模拟

为更加形象地说明相邻巷道围岩裂纹起裂扩展影响机理,借助ABAQUS 数值模拟平台对裂纹扩展过程进行仿真。扩展有限元(Extended Finite Element Method,XFEM)是一种求解不连续力学问题的有效数值方法,在传统有限元位移函数中加入跳跃函数及裂尖增强函数,对准确模拟真实的裂纹生长情况具有很好的效果。按照试件尺寸进行建模,并以PMMA 物理性能参数赋予材料属性;单元类型为CPS4,网格控制属性选择中性轴算法,试件划分为2 340 个单元;落锤设置预定义速度场。

试件动态裂纹扩展情况如图13所示。限于篇幅,以试件SA为例说明。试件顶部承受冲击荷载后,产生应力波向下传。图13(a)中,可见以落锤作用点为中心,应力云图呈现一个灯泡状的分布形态。图13(b)中,开始在两侧裂纹尖端处观察到应力集中的现象,应力云图在左侧裂纹AL 尖端处基本呈现对称分布,在右侧裂纹AR 尖端处则为非对称分布,这和图6 中的焦散斑形状分布规律一致。同时,可以观察到两裂纹尖端连线区域应力云图有重合。这表明,两处应力场出现了一定程度的叠加,应力场、能量场的相互影响,进而表现为裂纹起裂、扩展特性的差异。随着裂纹起裂扩展,可以观察到右侧裂纹AR 尖端处的应力云图逐渐消失,说明此处的应力场恢复到了受冲击荷载作用前的状态,这和第3.3节的动态应力强度因子变化情况一致。图13(c)是裂纹扩展过程中的应力云图分布,可以看到,在左侧裂纹AL 尖端处,应力云图近似“椭圆”状分布形态,对称分布的应力云图进一步说明左侧裂纹是Ⅰ型裂纹,验证了3.2 节和4.1 节的分析。图13(d)为裂纹扩展临近试件顶部时的应力分布情况,可见裂纹尖端的应力云图和顶部边界处由于应力波反射产生的局部应力云图相互接触融合。此后,裂纹扩展过程在很短时间内结束,也即失稳扩展的过程。观察图13(d)中的裂纹扩展路径,也和实验结果相符。

图13 动态裂纹扩展示意图Fig.13 Schematic diagram of dynamic crack propagation

5 结论

以PMMA 材料制作双截面巷道模型,借助新型数字激光动态焦散线实验系统和落锤加载平台进行冲击实验,控制变量为右侧预制裂纹偏转角度α,通过实验分析得到以下结论:

(1)当相邻巷道右侧截面裂纹向左偏转时,左侧裂纹的起裂韧度会有所下降,为1.01 MN/m3/2,裂纹较容易起裂。可见,相邻巷道围岩的裂纹起裂不同于单个截面巷道,会受相邻巷道截面的影响。

(2)左侧巷道顶部裂纹起裂后的动态应力强度因子变化有一个平台段,即稳定扩展阶段,持续时间在160 μs 左右,受相邻截面裂纹偏转角度α的影响并不明显。

(3)随着右侧巷道顶部裂纹向右偏转逐渐远离左侧截面时,左侧截面的裂纹扩展受抑制程度减弱,主要表现在起裂后的扩展速度会有所增加。

(4)左侧巷道截面裂纹尖端在应力波的作用下,以形成Ⅰ型裂纹为主;右侧则由于偏转角度的变化,在正应力和剪应力的耦合复杂应力场作用下形成复合型裂纹。