多孔介质渗透迂曲度理论推导与实验验证

薛东杰赵艾博刘奎昌侯孟冬付艳艳辛翠徐颜卓

中国矿业大学(北京)力学与建筑工程学院,北京 100083

“渗”这个字意味着液相或气相在固相的空隙中发生空间移动,尤其是多孔介质中,固相并非连续分布,不同尺度的孔裂隙互相交错并连通,为流相的渗透提供了几何空间。渗透、渗流和突渗是流相发生转移的不同层次,对应着安全和灾害的转换过程。自然界中渗透现象广泛存在,但当科学家开始研究其规律和内在本质时才发现,问题的层次性依然存在。如规律性的实验展示了在层流特定条件下,某些物理量之间存在着可基于类似Darcy 定律描述的线性关系。但是当渗透向渗流甚至突渗行为转变时,非线性带来的挑战困难得多,如Navier-Stokes 方程的理论求解成为历史难题;突变时的临界特征和临界力学理论仍处于建立之中。这些难点的解决需要观察视角的转换。“渗”意味着一种相互作用,液相在固相的空隙空间中发生转移,若在几何模型上将固相剔除,可获得空隙几何结构,理论上将空隙结构作为边界条件。基于Navier-Stokes 方程建立流体力学模型即可获得流动规律的求解,这种观察视角是不考虑固体力的相互作用,而是仅仅从几何约束的条件下考虑的。可见,相互作用尤其是力的相互作用在固相-液相间的描述常常是被忽略,而从几何约束的角度来体现相互作用,本质上是一种几何约束。

多孔介质的空隙结构几何复杂性远超人们想象,从几何角度来破解理论难题是科学家关注的焦点;而工程师往往关注的是宏观渗流规律,对于渗透、渗流和突渗行为转换过程中的强非线性只能依赖几何角度求解,裂隙网络几何复杂且在应力作用下会发生连通,形成新的几何网络,问题变得更加复杂。迂曲度是描述裂隙网络弯折效应的一个结构变量,其并不直接描述裂隙几何,而是描述其复杂性。弯折性反映了流体通过固相路程的难易程度,如在土壤中发生渗透远比岩石中容易[1],相应的迂曲度也要小很多。在深地煤炭开采工程[2-3]、地下盐穴储气库工程[4]及花岗岩封存高放核废料工程[5]中渗透性等评价也是工程重中之重。

在裂隙网络几何描述问题解决之前,力学建模和试验也是重要的研究手段。例如,基于分数阶理论建立渗流模型用以描述非饱和渗流问题[6];模拟煤样在三轴加载过程中的流固耦合[7];揭示岩石破碎后的非线性渗流行为[8]。这些模型的建立的依据和试验过程的准确解析都需要对裂隙几何进行精准描述。但事实是,精准测量低渗岩体内部的空隙结构是十分困难的,设备精度和视野总是存在不可协调的矛盾,高精度设备无法测量大尺度样品;大尺度样品又难以探测各种尺度的裂隙[9-10]。若结构不明或不准确,在定量计算迂曲度时就无法直接依赖试验所测的裂隙几何数据,因此迂曲度的理论计算仍存在着巨大挑战。通过试验也可间接得知迂曲度的一些特性,根据Carman-Kozeny 经验公式,多孔介质渗透率与毛细管迂曲度近似呈反比关系[11];孔隙度迂曲度存在正向关系[12-16]。因此,采用渗透率相关原理间接测试迂曲度也是主要方法,即采用理论与实验结合的方法可有效避免直接采用几何测量方法的误差。Purcell 较早提出用汞开展毛管压力与渗透率测试[17],但其忽略了迂曲度的影响,导致渗透率误差较大[18-20];Boundreau 对有限颗粒构成的迂曲度开展了建模研究[21];Sen 等认为孔隙结构空间分布具有自相似性,即迂曲度可利用分形理论来研究[22]。

对于流体,迂曲度和涡流等现象的关联也是研究热点[23-24],但迂曲度的定义来源及演化十分复杂。早期对迂曲度的认识仅是对渗透率的误差修正,随着认识的深入,赋予了迂曲度明确的物理意义,即反映孔隙结构流程的弯曲程度,才禀赋了其内在物理意义[25],国内也有文献提出直接用孔隙度计算迂曲度[26],认为迂曲度曲线具有分维特征[27],提出了分形毛细管力模型[28]。

笔者基于毛细管模型,根据Hagen-Poiseuille 公式与达西定律建立普适的迂曲度表达式,并针对低渗介质提出了一种适用于毛细管力特征明显的迂曲度表达式,建立了迂曲度分形维数。针对分叉现象,在满足质量守恒前提下,分析了分叉孔道母孔子孔几何关系,并指出分叉现象的产生并非完全随机,而是在满足优化能量前提下的理想分配,验证了Murray 定律,也适用于岩石孔裂纹系统。本文以盐岩为案例,验证了表达式的适用性与可靠性。研究结果可为求解多孔介质材料迂曲度提供理论与实验参考。

1 迂曲度建模及分形维数计算

孔隙通道包括非有效连通部分(盲孔)及有效连通部分。连通性描述是揭示流体流通的重要基础。通道方向分布具有不确定性,截面形状与尺寸大小位置分布具有随机性,在水力、温度等外界因素影响下还可能存在着开闭状态的转换,这些复杂因素都给认识孔隙结构空间分布带来挑战,因此从统计理论上分析更具有现实意义。基于此,本文将孔隙通道假设为毛细管模型[25](图1)。

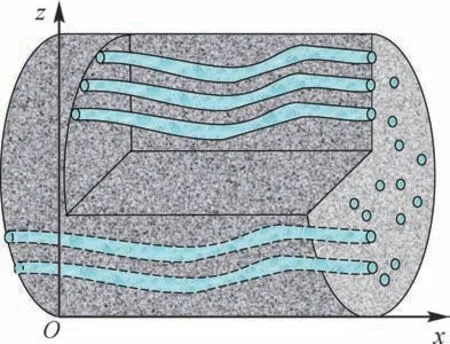
图1 毛细管模型Fig.1 Capillary model

如图1所示,假设毛细管道在截面xz上均匀分布,毛细管孔道形状相同,孔道中流体单相、饱和,其运动规律符合达西定律。微元体截面xz面积为A,单位面积分布毛细管根数为n,每根毛细管弯曲度为τ,孔道截面形状为圆形,半径为r,单根孔道体积为V,单位横截面密度为N。迂曲度定义较多[29-31],Le表示流动路径长度,定义迂曲度[29]

一种方法是根据Hagen-Poiseuille 公式[32],则通道流量q为

式中,Δp为压差;μ为黏滞系数。

根据达西定律:

式中,K为渗透率。

定义孔隙度[33]

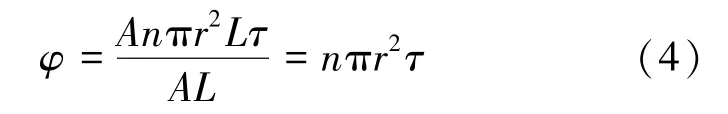
联立式(2)、式(3)与式(4)得

引入水力学半径平均值Rh,则

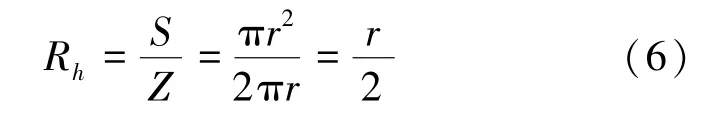
式中,S为流体流过总截面积;Z为总湿润周长。

根据经验[34],存在如下关系:

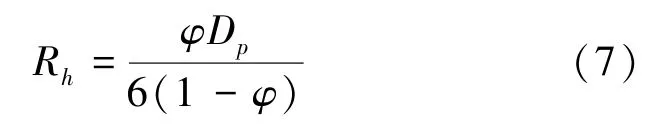
式中,Dp为粒子平均半径。

结合式(5)、式(6)与式(7),得迂曲度

假设系统由N个球形毛细管粒子构成,则

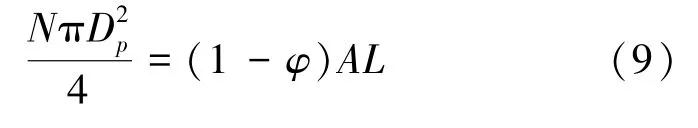
对应的,迂曲度可定义为

另一种方法是利用毛细管压力公式[25],较大孔径孔隙通道并不存在典型毛细现象,其适用范围需要界定,则单根毛管压力[31]

式中,σ为界面张力;θ为接触角。

结合式(2)得

联立达式(3)得

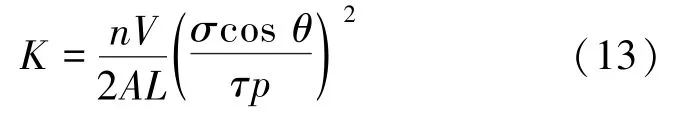
考虑饱和度s,则式(13)可改为

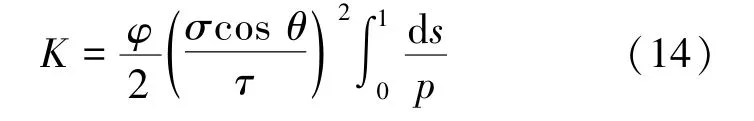
则迂曲度重新定义为

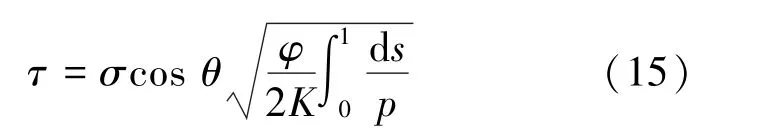
假设所有毛细管压力p相同,则

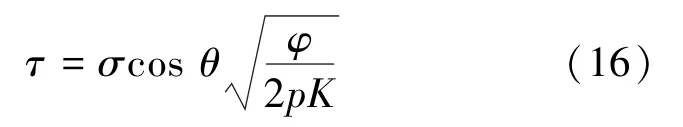
利用式(15)和式(16)即可测定迂曲度。Wheatcraft 和Tyler 建立了多孔介质迂曲流管特性的分形标度关系[34]:

则

式中,λmin为毛细管孔径的最小值;DT为迂曲度分形维数。

对于线性孔道渗流,1≤DT≤2。

联立式(15)与式(18)得

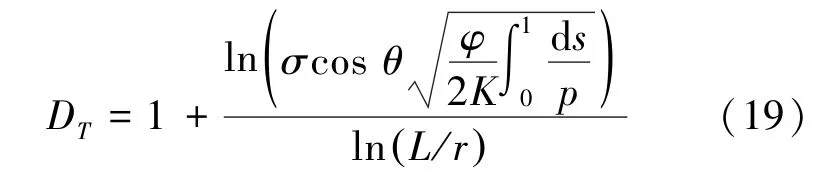
式(19)说明利用压汞实验可以确定迂曲孔道分形维数。定义分形影响系数:

当迂曲度分形维数DT确定时[图2(a)],即毛细管道弯折程度一定时,分形影响系数与长径比近似成线性关系。如图2(b)所示,当毛细管孔道长径比确定时,分形影响系数与迂曲度分形维数呈非线性关系,DT与L/r越大影响越明显。如当L/r≤5 时,变化不大,此时可以忽略DT的影响,由此可知当考虑DT对的影响时,需要考虑DT是否在长流程环境下,当L/r≤5 的短流程环境时,孔道长度和直径在一个数量级上,孔道弯折性不显著,弯折性对流体的阻滞作用不明显;另一方面说明,粗糙性特征至少精度上要高于流程定义,并且应考虑粗糙在流程上的非线性积分。

图2 长径比和迂曲度分维与分形影响系数的关系Fig.2 Fractal coefficient influenced by the aspect ratio and fractal dimension of tortuosity

2 分叉孔道迂曲度特征分析

通常在描述孔、裂隙通道时会隐含假设,即通道始终是1 条,不存在1 条通道连接2 条孔道甚至更多。分叉现象总是被刻意忽略或者简单地统计长度。这是因为分叉会引起更多的非线性特征,如分流现象;分叉孔道给分维的计算带来挑战。

裂纹分叉是普遍存在的,应引起足够的重视。自然界中材料分布与裂纹生长过程并非完全随机现象,最优化能量的分配与传播控制着裂纹生长[35-36]。合理的能量分配最终导致裂纹的半径与长度生长相互影响,形成具有规律性的网络系统。天然生成的孔道具有同样的规律,虽然能量形式释放机制迥异,但都遵循最小化能量的原理。

利用科林斯定义仅统计分叉毛细管长度意义不大,有较多的局限性,首先无法表征长程单条孔道粗糙度及迂曲度的特征,其次忽略了迂曲度对孔道渗透特性的界定。基于迂曲度定义,为了更好地反映渗透特征,有必要建立考虑分叉孔道特性的迂曲度模型。

母孔设为分叉前的单一孔道,子孔为由母孔分叉而来的多条孔道。考虑最简单分叉(1 分2)(图3),考虑流体从总孔道(标号为0,下同)分叉分别流向叉道1 与叉道2。总孔道长度为L0,迂曲度为τ0,等效半径为r0,流量q0,对应的分叉1 物理意义:L1、τ1、r1与q1;分叉2 物理意义:L2、τ2、r2与q2。

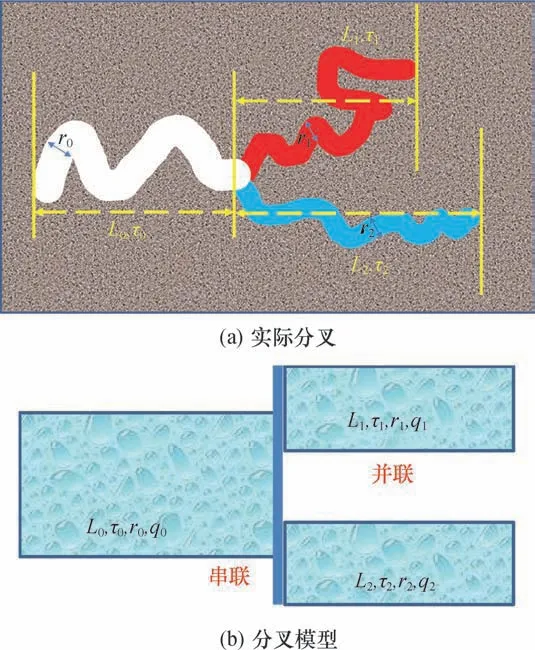
图3 分叉示意图Fig.3 Bifurcate path of capillary

根据式(2)可得流体持续流动所需要的能量:

孔道表面粗糙性引起的流体能量耗散:

式中,η为表面粗糙性系数。

总的能量:

根据最小能量原理,对式(23)求微分,得

式中,ξ为表面粗糙性系数。

可见,流量与孔径的立方成正比,这与平行板立方体定律相似。平行板定律是由实验总结的,而式(24)是基于Hagen-Poiseuille 公式理论推导的结果。

根据质量守恒q0=q1+q2,对母孔0、子孔1、2同时使用式(24)得

母孔孔径的立方等于子孔孔径的立方和,即Murray 定律[37-39],说明Murray 定律适用于岩石孔裂隙系统。

定义流阻:

母孔与子孔串联,两子孔并联,则总流阻为

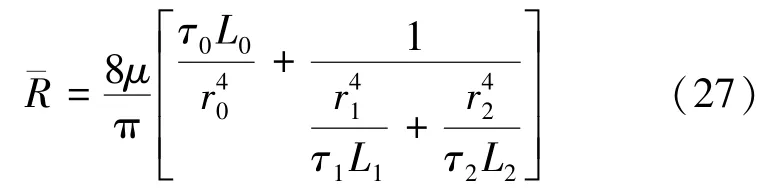
考虑分叉结构的体积,即流量的总体积:

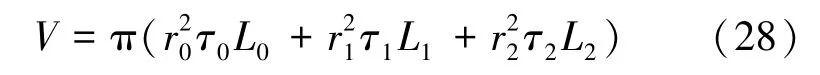
定义Lagrangian 函数:

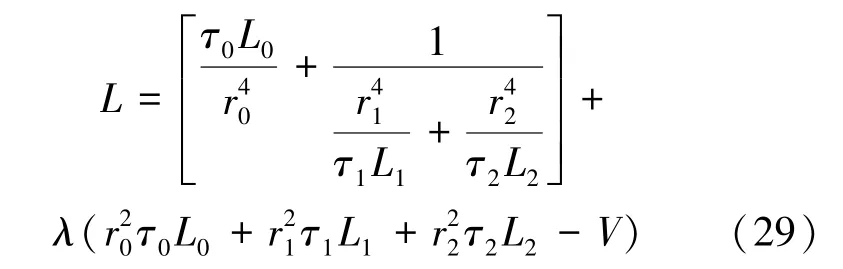
分别对r0、r1与r2求极值:

式(30)化简后同式(25)。再次验证了岩石裂纹分叉孔道满足Murray 定律。

将分叉孔道整体考虑,则总能量:

等效迂曲度:

忽略粗糙性,则

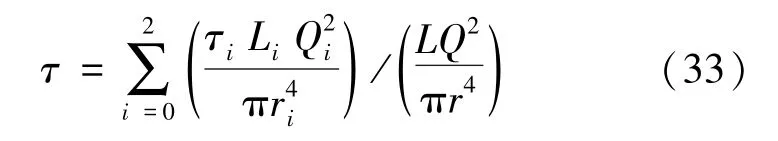
3 低渗盐岩毛细孔道迂曲度计算

盐岩是天然气储藏、核废料等有害物质封存的理想地下场所,低渗现象是其致密的孔隙结构导致的。样品源于湖北应城盐矿,主要成分为石盐,含少量石英。加工成几何尺寸为直径25 mm、高30 mm 试样,进行高压压汞实验。实验前利用工业CT 对孔隙扫描,精度为30 μm,难见孔隙分布,可见盐岩孔隙尺寸十分微小(图4)。设计压力范围0.1～226 MPa,对应孔隙尺寸为7.5 μm～3.2 nm,连续加压,进汞速度控制7 MPa/min,设备精度为0.01%。

图4 盐岩取样、加工及CT 扫描Fig.4 Drilling and processed sample for CT scanning

图5 为所得到的毛细管压力曲线,初始压汞从0.008 MPa 开始,迅速增长至30 MPa,此时对应的汞饱和度从0% 到接近10% ;然后压汞曲线变得平缓,压力从30 MPa 到最大值200 MPa,对应汞饱和度从10% 到70%。本样品30 MPa 是汞饱和度出现急速变化的拐点,将压汞曲线分为两个部分。30 MPa 之前,汞进入的都是大孔隙,但这种空隙结构并不多对应的汞饱和度不高。30 MPa 之后,压力突破了拐点,毛细管孔开始连通,汞饱和度迅速增长,但高压下盐岩可能会出现损伤,所测饱和度并非原始状态的孔隙特征。之后从200 MPa 开始急速回汞到40 MPa,但汞饱和度维持在70% 几乎没有变化;之后回汞到0.015 MPa 对应的汞饱和度下降至45%。可见,在不同的压力下孔道的有效连通对汞饱和度影响较大。侧面验证了盐岩结构的复杂性和致密性。根据实验测定本样品盐岩孔隙度φ=6.5%,渗透率K=0.001md,取汞的界面张力σ=0.48 N/m,接触角θ=140°,利用式(15)结合图5 数据积分,可计算得到盐岩迂曲度τ=58.32。常规计算方法得到的迂曲度普遍小于5,本方法测定的迂曲度是其十几倍,更符合真实情况。盐岩迂曲度较大,说明复杂分布孔道形成的渗透路径曲折,最终造成流体通过困难,即盐岩低渗的主要原因是低孔隙度和高迂曲度。

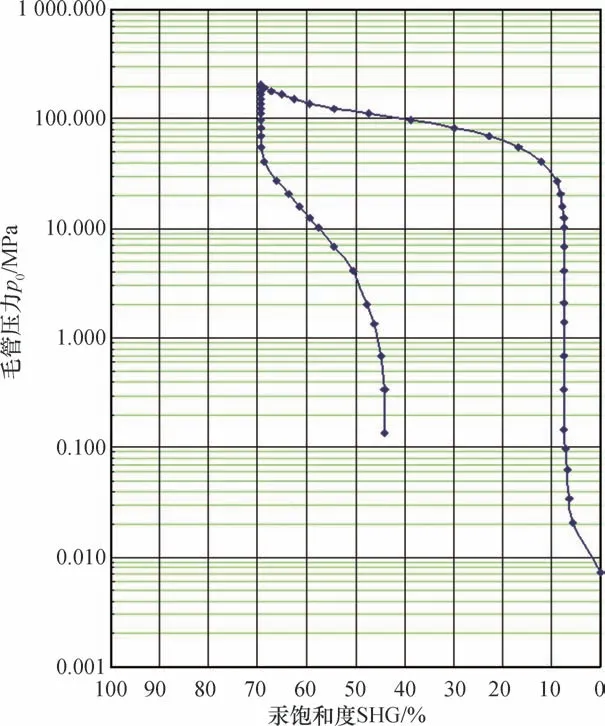
图5 毛细管压力曲线Fig.5 Curve of capillary pressure

4 结论

低渗孔隙介质如盐岩内部的空隙结构几何和拓扑精准表征在数学上是很大的挑战,多数工作关注了几何信息,而忽略了拓扑连通等核心变量。用于描述空隙结构的几何变量较多,但普适性的关键几何或拓扑变量并未最终确定。渗透的本质是连通,连通性描述的数学基础是拓扑几何理论,因此,有必要在传统迂曲度几何定义的基础上开展拓扑几何描述研究。本文尝试从最简单的分叉模型推导出迂曲度的理论表达式,但与圆形毛细管模型等相比,表达式仍差异较大。可见,迂曲度的理论推导实现普适性应用仍任重道远。

(1)考虑流通孔道的分形特性,引入迂曲度分维,并推导了迂曲度分维确定的实验公式,这是一种基于压汞实验求解分维的新方法。定义了分形影响系数,当迂曲度分形维数DT确定时,分形影响系数¯λ与长径比近似成线性关系。当长径比确定时,分形影响系数¯λ与迂曲度分形维数DT呈非线性关系。

(2)针对分叉孔道,流量与孔径立方成正比关系,在满足质量守恒前提下,分叉孔道母孔孔径的立方等于子孔孔径的立方和,从两个方面验证了岩石裂纹分叉孔道满足Murray 定律,推导了分叉孔道等效迂曲度数学表达式。以盐岩渗透为案例,低孔隙度、高迂曲度是盐岩低渗的主要原因。