考虑全生命周期的露天矿边坡时效稳定性分析

包敏陈忠辉王雄杨继海申作栋

中国矿业大学(北京)力学与建筑工程学院,北京 100083

与水利工程边坡对长期稳定性要求较高不同,露天矿高边坡不追求长期稳定性,在边坡服役年限内保证“安全使用”即可。由于露天矿高边坡的稳定性与时间变化密切相关,边坡越高时效性越显著并且具有复杂的非线性,因此有必要对露天矿高边坡整个生命周期内的稳定性进行研究,将边坡的稳定性分析由传统的非时效系统全面推向时效系统[1]。周创兵[2]提出了全生命周期的理论并对水电工程高陡边坡的时效性进行了分析。

目前,国内外关于露天矿高边坡的时效性研究主要集中在边坡蠕变特性和锚索预应力损失两个方面。才庆祥等[3]提出了时效边坡的概念,实现了端帮边坡由永久性设计向时效性设计的过渡。芮勇勤等[4]在老化理论的基础上提出了软弱夹层的一般流变方程。陈宇龙等[5]将混凝土材料时域相关的断裂行为分为短时动态冲击破坏和长时间稳态的蠕变断裂行为。Kemeny[6]建立了断裂力学模型,指出了不连续面破坏的原因是岩桥的时变破坏。Shao 等[7]研究了岩石力学性质随时间的劣化,对岩石蠕变特性进行了模拟。刘波等[8]采用随机介质理论对地铁隧道随时间变化的沉降进行了预测,获得了地表差异沉降及地表沉降曲面随时间的变化规律。陈国庆等[9]利用动态强度折减法实现了对边坡失稳全过程的进一步分析和调控。李连崇等[10]基于岩体的流变特性,在分析软弱结构面的时效破坏模式时引入了强度退化模型。程辉等[11]采用单体锚索防治巷道底鼓现象,现场应用效果良好。朱晗迓等[12]将锚索与边坡体进行耦合,推导了锚索预应力的长期损失计算公式。左建平等[13]提出了深部巷道等强支护控制理论力学模型。

已有的研究分析了蠕变的劣化效应,而没有考虑其对边坡安全系数时效性的影响。考虑了锚索预应力随时间的变化,但是没有与蠕变型边坡工程的全生命周期相结合,没有达到经济、安全的双重目标。因此,本文根据露天矿高边坡的稳定性受到开挖和蠕变劣化的共同影响,引入了岩石强度劣化理论,推导了时间效应下安全系数的计算公式,提出了全生命周期内边坡的稳定性变化模型。考虑锚索的预应力损失和边坡蠕变现象,建立了预应力损失条件下蠕变型边坡安全系数的表达式。最后以大孤山西井边坡为例,借助FLAC3D内置的FISH语言把劣化理论嵌入到强度折减法中,利用改进的强度折减法计算边坡的时效安全系数,通过与实际工程对比验证了改进理论的可靠性。

1 全生命周期内边坡稳定性分析

1.1 边坡稳定性变化模型及研究主线

露天矿高边坡的稳定性受边坡开挖和蠕变劣化的双重影响,开挖深度越大,蠕变效应越显著,边坡越容易失稳。边坡稳定性变化模型如图1所示。当边坡稳定性不能满足安全生产的要求时,需要对边坡进行加固,加固措施包括锚杆(索)、挡墙、钢筋混凝土抗滑桩以及削坡减载等[14]。进行合理的加固后边坡的安全系数会显著提高,但是伴随着边坡开挖深度的增加以及加固设施的劣化,安全系数会下降,降至一定程度就需要进行二次加固,以保证边坡在全生命周期T内的稳定性。同时,进行锚索方案调控,使得边坡在全生命周期结束时,最终的安全系数趋近于1,安全储备最小,达到全生命周期内边坡既安全又经济的目的。

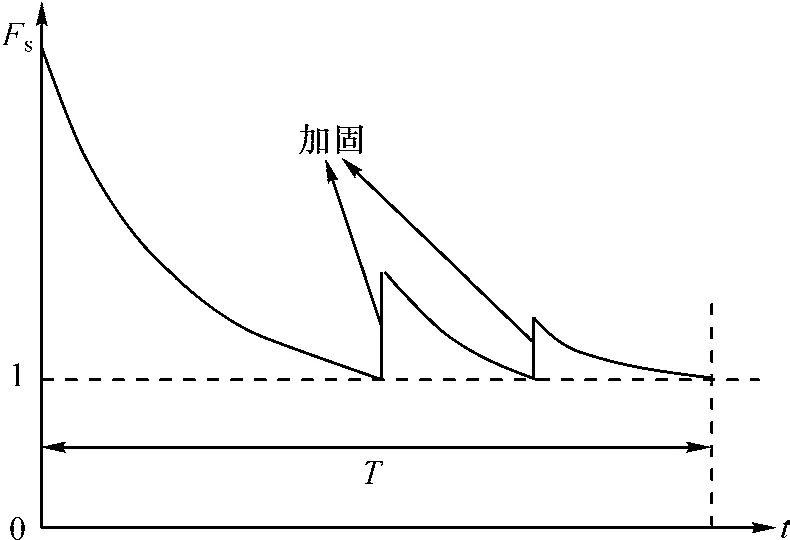
图1 边坡稳定性变化模型Fig.1 Change model of slope stability

本文沿理论分析与数值计算的主线展开全生命周期内边坡的稳定性研究,如图2所示。首先建立蠕变劣化理论下边坡安全系数的动态表达式,并开展时变稳定性与纯开挖情况的对比,然后基于全生命周期进行失稳情况下的方案调控,最后运用至边坡的实例分析中。

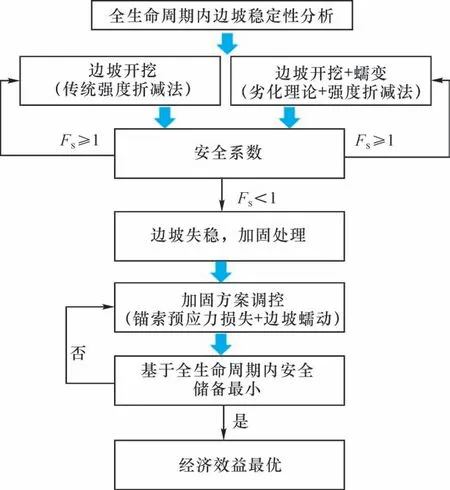
图2 边坡稳定性研究主线Fig.2 Main line of slope stability study

1.2 强度劣化理论

开挖深度的增加,导致露天矿高边坡暴露面积增大、暴露时间增长,岩土体由于蠕变效应而劣化,具体表现为岩石强度随时间增长而衰减[15]。本文将劣化理论引入安全系数的定义中,获得的时效安全系数能更加直接客观地反映边坡的时效非线性。

假设已知边坡潜在滑动面为AB,滑动体为ABC,把自重力G分别平行和垂直于滑面分解,对边坡进行受力分析,如图3所示。

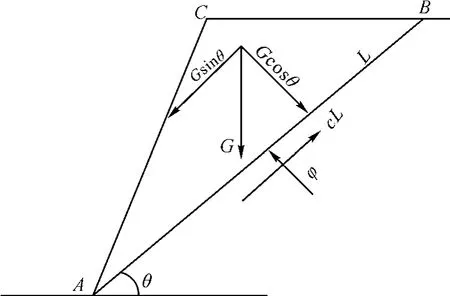
图3 边坡受力分析Fig.3 Stress analysis of slope

边坡滑动面产生的抗滑力R为

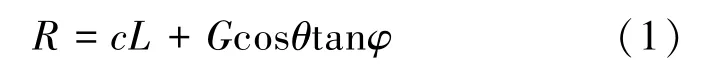
式中,c、φ分别为滑动面上的黏聚力和内摩擦角;θ为滑动面与水平面的夹角;L为滑动面的长度。

边坡滑动面受到的下滑力S为

由定义可知,安全系数Fs的表达式为

边坡的蠕变劣化效应主要表现为边坡岩体参数随时间的增长而降低,文献[16]得到了强度参数随时间的衰减曲线,如图4所示。

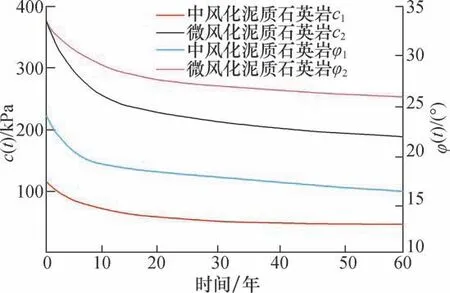
图4 强度参数时效曲线Fig.4 Aging curves of strength parameters

因此,根据强度参数的时间效应,将黏聚力和内摩擦角表示为时间的函数c(t)、φ(t),通过引入劣化因子Dt来表明岩体的劣化行为。根据张强勇等[17]的研究,Dt可设为

式中,Et为任一时刻的弹性模量;E0为初始弹性模量。

当t=0 时,Dt=0,表明在初始时刻岩体没有被劣化;当t→∞时,E∞→0,Dt=1,岩体被完全劣化,E∞为考虑蠕变劣化的长期弹性模量。在劣化过程中,E∞≤Et≤E0,劣化因子Dt逐渐增大但始终小于1,因此上式可以演化为

式中,a是与劣化程度相关的系数,a值越大,劣化程度越大。

将劣化因子代入黏聚力c(t)和内摩擦角φ(t)中,得

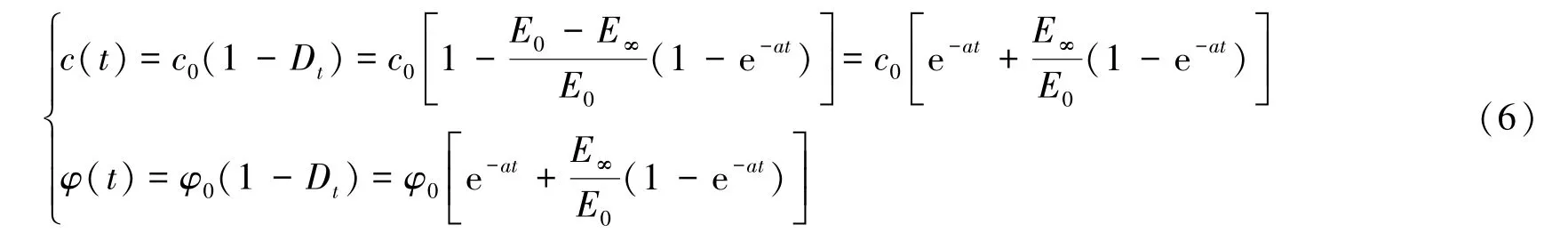
式中,c0、φ0分别为初始黏聚力和内摩擦角。

将式(6)代入安全系数中,则边坡时效安全系数Fs(t)的定义式为

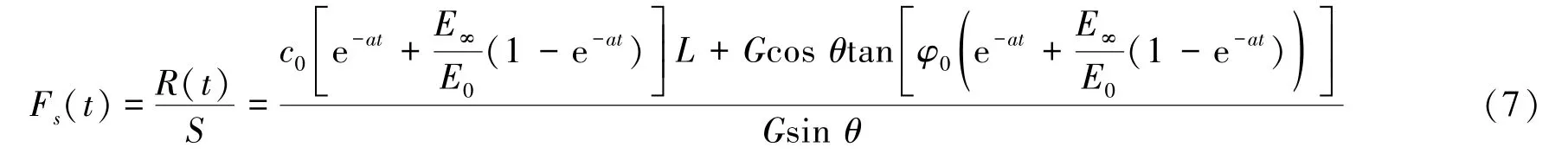
根据劣化理论得到的安全系数是关于劣化因子的函数。随着时间的延长,边坡滑面的下滑力不变,抗滑力逐渐降低,时效安全系数与岩石强度参数也逐渐降低。露天矿高边坡是一个时变系统,边坡的输出响应与其强度参数劣化的时间长度有关。对边坡的稳定性评价中,时效安全系数综合考虑了岩土材料参数在时间上的变异性和不确定性,符合边坡的实际情况,能更好地服务于露天矿高边坡的全生命周期。

1.3 锚索加固后的稳定性分析

1.3.1 锚索加固机理

在露天矿开采过程中会采取一定的加固措施以确保工程安全、顺利地进行[18]。对于稳定性要求较高的边坡,一般采用预应力锚索加固。预应力锚索属于主动受力,加固的实质是通过施加预应力将锚索与边坡岩土体串联在一起,使得作用区域内的岩体处于高围压的三向应力状态,形成承载圈[19],达到加固边坡、提高稳定性的目的。锚索的锚固机理如图5所示。

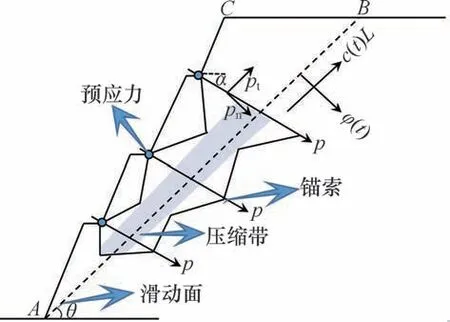
图5 预应力锚索锚固机理[18]Fig.5 Reinforcement mechanism of prestressed anchor cable[18]

1.3.2 时效安全系数

通过施加预应力,在锚索与锚固端周围形成压力锥体,内部岩体相互挤压形成挤压带[19],利用岩体抗压不抗拉的力学特性,有效地降低了边坡岩体的变形破坏,提高了边坡整体的稳定性。边坡锚固后结构面被压紧,滑面的应力状态受到影响,锚索预应力一方面提供抗滑力,另一方面增大滑面上的正应力,此时考虑蠕变劣化效应产生的抗滑力R(t)为

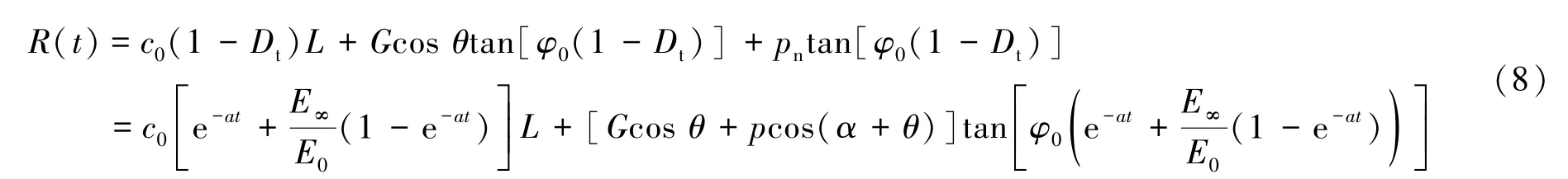
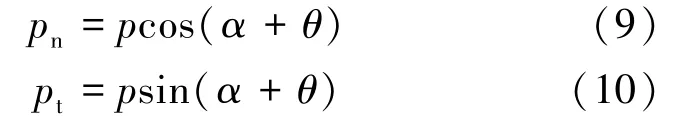
边坡滑动面受到的下滑力为

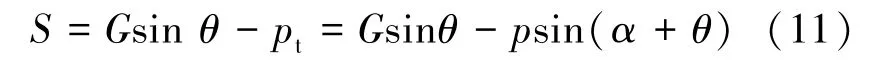
根据时效安全系数的定义,有

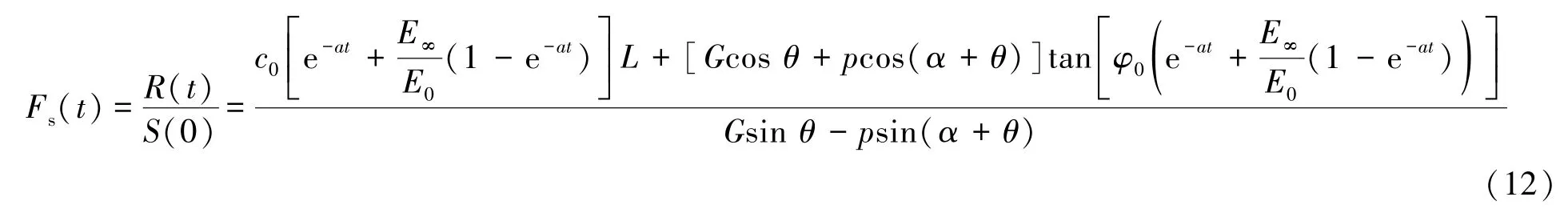
由上可知,边坡岩体属于时变系统,受劣化因子影响显著。在锚固初期,预应力的切向分力降低了边坡滑面的下滑力,法向分力增大了边坡的抗滑力,时效安全系数有明显的提升。边坡的蠕变变形必然导致预应力法向分力的损失,在边坡加固中,预应力损失是锚索不能满足边坡支护的主要原因[20],会加剧边坡的变形,进而导致时效安全系数的降低、增加边坡的失稳风险。所以,随着时间的增加锚固效应也具有劣化性,时效安全系数会在上升之后又逐渐降低。

2 工程实例分析

2.1 工程概况

鞍钢大孤山西帮巷道是大孤山带式输送的重要通道,边坡的稳定对巷道安全至关重要。本文选取西井边坡剖面4-4 进行分析(图6)。该剖面纵切西北帮楔形铁矿北边缘,剖面方位角117°。边坡主要出露地层为铁矿、绿泥片岩、石英绿泥化角岩、太古代花岗岩,坡内存在倾向于坡面的断层带F14,属于二级断裂构造,内部填充为闪长石英绿泥化角岩,倾角48°。边坡总坡高432 m,分为8 步开挖,目前边坡已开挖至-210 m,在台阶6-8 步开挖后边坡失稳。边坡变形最大的时期为2016年底到2017年7月,空间上对应-210 m 平台的坡脚开挖。2017年9月至今,-210 m 平台继续作业,同时期边坡蠕变变形再次加剧。

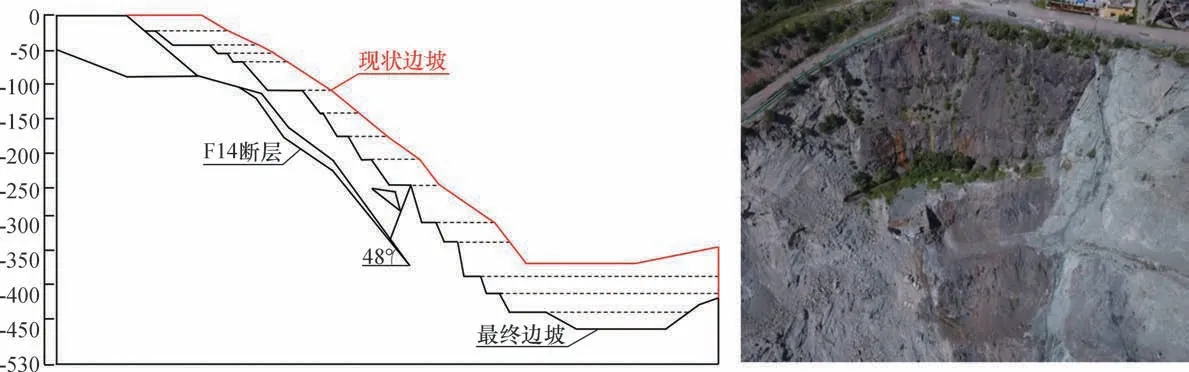
图6 西帮边坡4-4 剖面图Fig.6 West side slope 4-4 section view

2.2 数值模拟

依据露天矿边坡4-4 剖面图,建立了西井边坡的数值计算模型(图7),模型共有节点37 191 个,网格单元67 660 个。模型的约束条件:边坡顶面为自由面不加以约束,左右侧面分别进行法向约束,底面采用x、y、z三个方向的固定约束,只考虑岩体自重。开挖模型采用Mohr-Coulomb 屈服准则,蠕变模型选取Burgers 模型嵌入Mohr-Coulomb 准则的复合黏弹塑性流变模型如图8所示,式(13)为一维本构关系[21]。考虑蠕变劣化作用,将黏聚力和内摩擦角关于时间劣化的表达式代入强度折减法中计算安全系数。根据前期研究资料及后期现场试验、室内试验资料,对选取的边坡岩石参数进行统计分析及试算验证,最终确立采场边帮岩体计算参数数组见表1。

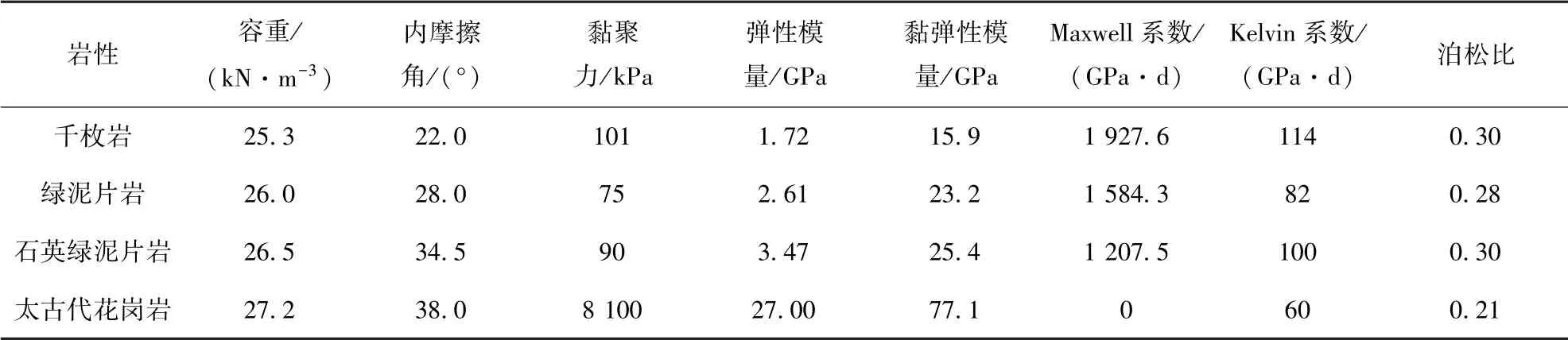
表1 边坡岩体力学参数Tab.1 Rock mechanics parameters of slope

图7 数值计算模型Fig.7 Numerical calculation model

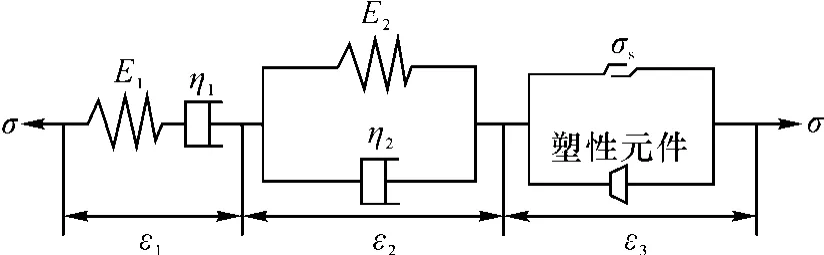
图8 蠕变本构模型Fig.8 Creep constitutive model

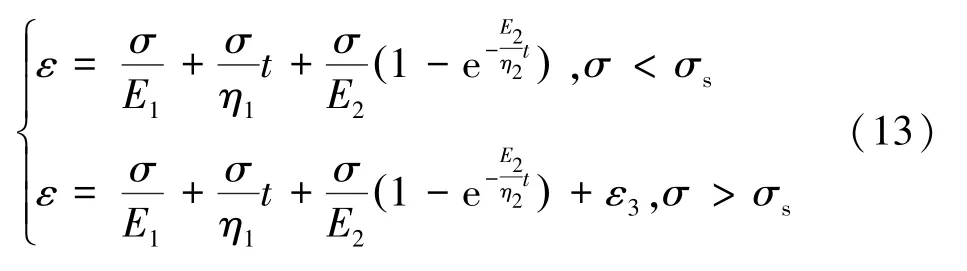
式中,E为弹性模量;η为黏滞系数;ε3为塑性体变形量;σs为塑性体屈服应力。

根据边坡的设计方案,达到-210 m 前分8 步开挖,最终边坡开挖完成一共分14 步,从上到下依次进行。边坡在-210 m 平台出现失稳,因边坡深度较大又有断层影响采用锚索加固,锚索参数见表2。考虑不同的加固方案,寻找安全储备的最小值,确定最优支护方案。同时,观察边坡坡面位移的变化情况,在台阶1、4、5、6、7、9 设置6 个监测点进行位移监测。

表2 锚索力学参数Tab.2 Rock mechanics parameters of slope

2.3 结果分析

2.3.1 安全系数及监测点位移分析

大孤山西井边坡属于超高边坡,安全等级为Ⅰ级,自然工况下安全系数为1.10 ＜Fs＜1.20 时,边坡基本稳定;1.0 ＜Fs＜1.10 时,边坡属于欠稳定;Fs＜1.0 时,边坡不稳定。

首先,根据式(5)计算得到劣化因子Dt后代入式(6),得到了黏聚力和内摩擦角随时间的劣化曲线。图9 分析断层的强度参数黏聚力和内摩擦角,将考虑蠕变劣化与不考虑蠕变劣化两种情况的参数进行对比分析。观察可知,在不考虑蠕变劣化效应的情况下,黏聚力和内摩擦角随开挖步数的增加保持为常数;考虑蠕变劣化效应时,黏聚力和内摩擦角随开挖步数的增加呈“L”型曲线降低,最终趋于稳定值。

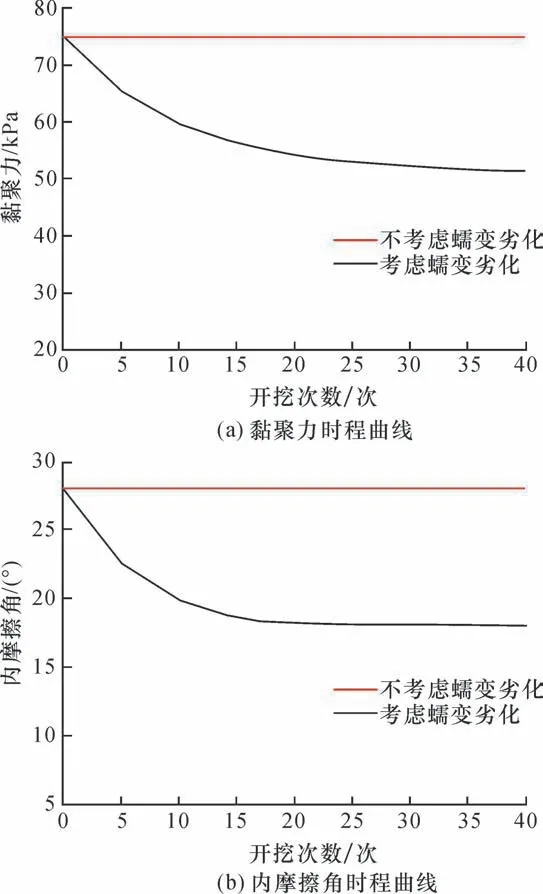
图9 强度参数时程曲线Fig.9 Time history curves of the intensity parameters

其次,利用改进的强度折减法计算安全系数,对比边坡是否考虑蠕变两种情况下的安全系数,结果如图10所示。可见,开挖和蠕变都会导致安全系数的降低。然而只考虑开挖时,边坡在第8 步开挖后安全系数为1.58,不会失稳;在既考虑开挖又考虑蠕变时,安全系数下降趋势更加明显,在第8步后安全系数为0.98,边坡失稳与实际工程吻合。综上所述,考虑蠕变的劣化效应,更能准确地评价边坡稳定性。

图10 安全系数时程曲线Fig.10 Time history curves of the safety factor

2.3.2 位移分析

随着边坡开挖深度的增加及蠕变条件的改变,断层软弱填充物蠕变劣化效应明显,位移值较大,如图11(a)所示。西井边坡标高-70 m 至-210 m位移量较大,其中最大处位于-120 m 至-210 m 坡段。潜在滑动面后缘位于-68 m 平台及以下坡面,并沿F14 断层软岩风化带向下延伸,从-210 m 附近剪出,与时效安全系数在第8 步之后失稳一致。

在图11(b)中选取断层附近的2 个监测点,对比分析考虑蠕变劣化影响的位移曲线图。由图可知,边坡的位移主要由于开挖卸荷产生,蠕变作用下边坡的变形与卸荷回弹产生的变形方向相反,所以考虑蠕变的边坡位移值在初始阶段要低于开挖卸荷产生的位移。在开挖卸荷作用下,监测点的位移先较快增长后逐渐趋于稳定,说明不在开挖影响范围内时,位移值变化不大。考虑蠕变劣化效应,监测点的位移一直保持增长趋势,不在开挖影响范围内,但是随着时间的延长,位移值继续增加。

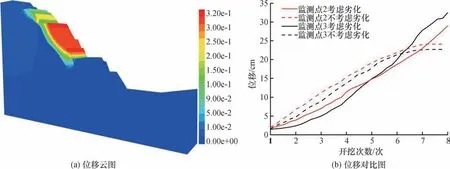
图11 边坡位移图Fig.11 Slope displacement diagram

2.4 锚索加固方案优化

2.4.1 初始设计方案

西井边坡开挖至-210 m 时边坡稳定性问题突出,边坡有向临空面滑出的危险。因此,在第8步开挖之后需要对4-4 高边坡采取预应力锚索加固及其他加固措施,这里主要研究预应力锚索的加固。根据设计方案,在坡面6 的上、下坡面单排分别加固4 根、5 根锚索,在坡面7 加固2 根锚索,在坡面8 加固7 根锚索;在-210 m 坡段采取预应力锚索+C30 肋柱加固,坡脚设C30 地梁。锚索的初始布置情况及对时效安全系数的影响如图12所示。

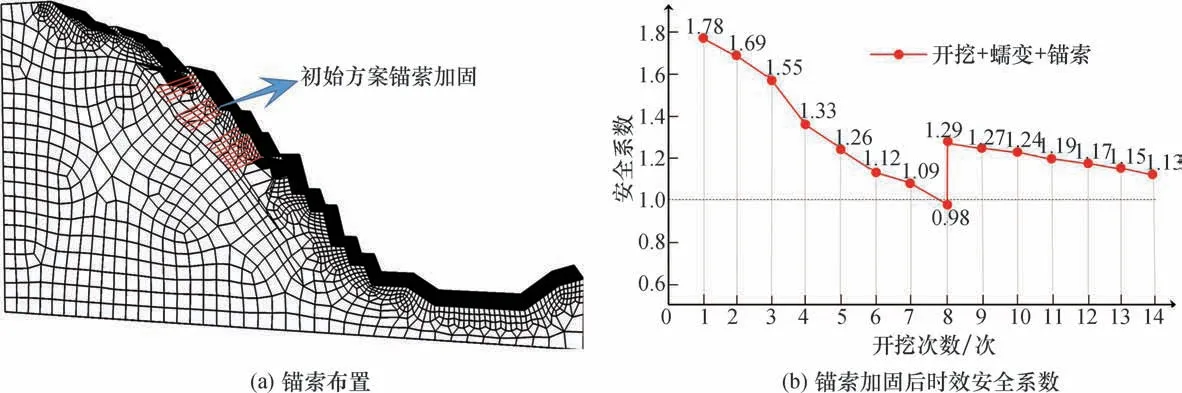
图12 初始加固方案Fig.12 Initial reinforcement scheme

当边坡达到服务年限后,仍能满足的安全系数与边坡安全系数临界值之差,称为安全储备。合理的安全储备值可以大幅减少边坡加固的资金投入。锚索加固初期,边坡时效安全系数会提高,考虑边坡蠕变对锚索预应力造成的损失,随着开挖的进行及蠕变的影响,时效安全系数又会逐渐降低,降低趋势会有所减缓。初始锚索设计方案最终的安全储备值为+0.13,安全储备值富余容易造成资源浪费、投资增加,所以在初始设计方案的基础上对锚索加固方案进行优化,寻找不同支护方案下安全储备的最小值。

2.4.2 锚索加固方案比选

根据位移分布情况对每一排的锚索加固方案进行修改,确定了3 种方案(表3)。

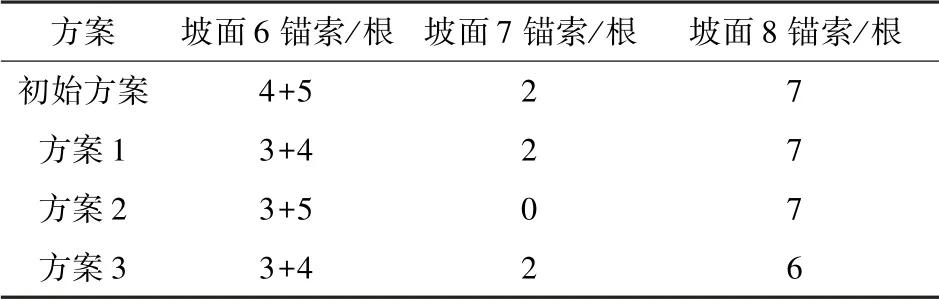
表3 锚索加固方案Tab.3 Anchor cable reinforcement scheme

不同加固方案安全系数的变化趋势如图13所示。观察可知,初始方案的安全储备值为+0.13,方案1 的安全储备值为+0.09,方案2 的安全储备值为+0.02,方案3 的安全储备值为-0.04。在保证边坡安全生产的前提下,方案2 的安全储备值最小。

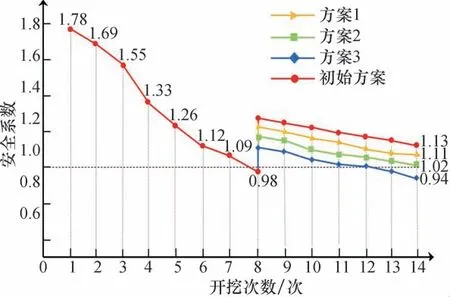
图13 不同加固方案安全系数的变化趋势Fig.13 Safety reserve value of different anchoring schemes

对边坡不同加固方案进行预算见表4。

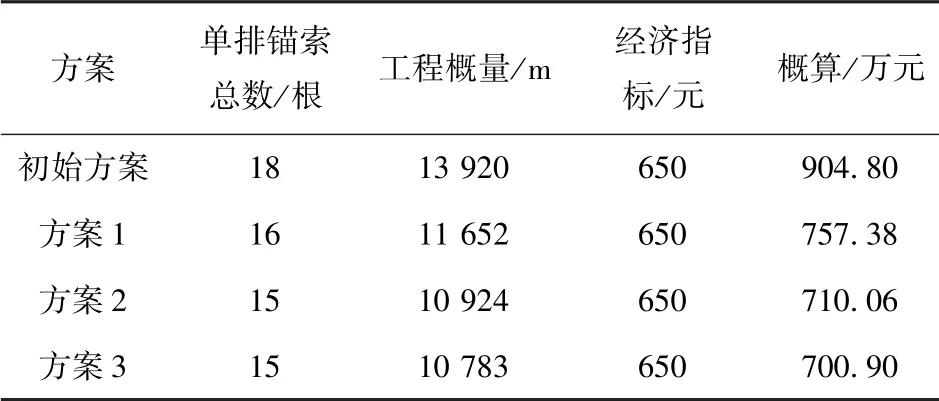
表4 加固方案预算Tab.4 Reinforcement plan and budget

由表4 可知,初始加固方案下边坡稳定性最高但概算也最高。初始方案与方案1 单排锚索相差2 根,总的概算差达到47.32 万元。方案2、3 由于锚索加固位置不同,在总数相同的情况下方案3 的概算低于方案2,但是稳定性不能满足要求。因此,在不考虑其他投入的情况下方案2 不仅能保证全生命周期内的稳定性,而且使得露天矿高边坡生命周期内投资最少、效益最优。

3 结论

(1)基于蠕变劣化效应计算岩石的强度参数,黏聚力和内摩擦角随时间均呈“L”型下降,最终趋于稳定。内摩擦角趋于稳定的时间值要小于黏聚力趋于稳定的时间值。

(2)对大孤山西井边坡进行实例分析,考虑开挖和蠕变过程计算得到的安全系数下降趋势更加明显,监测点位移一直保持增长趋势,不会在开挖结束后趋于稳定,与工程实际更加吻合。

(3)锚索加固初期法向分力锚固岩体,提高时效安全系数,受岩石强度劣化的影响,时效安全系数随时间增加,然后呈现下降的趋势。不同锚索加固方案对安全系数的提高程度不同,对比分析可以获得经济效益最优方案,满足实际工程要求。