软岩巷道挠曲型底鼓机理与底板桩基控制技术

郭东明亢鑫超陆志颖陈麒宇张伟赵志峰曹延鹏

1.中国矿业大学(北京)力学与建筑工程学院,北京 100083;2.江苏浩森建筑设计有限公司,江苏常州 213022

巷道掘进导致围岩应力状态发生改变,使表面围岩向巷道内移动,这种现象称为底鼓[1]。底鼓是一种典型的非线性力学现象[2-4],底板支护强度和围岩力学参数决定了底鼓的量级。一般情况下,当底鼓量级较低时,不需要专门治理措施。但在巷道掘进过程中,由于底板没有支护强度,使底鼓引起了顶底板巨大的移近量,进而极易诱发巷道失稳和底板突水等次生灾害[5-6]。

当巷道位于高应力环境时,巷道底板围岩在平行于岩层的挤压应力下向临空面发生失稳破坏。这种底鼓一般认为是挠曲褶皱型,多见于埋深较大、底板围岩软弱的掘进巷道中,也是底鼓的常见类型。学者从不同角度对其产生机理进行了研究。姜耀东等[7]通过模型试验研究了挠曲型底鼓的破坏形态和破坏范围,指出底板围岩力学参数、围岩应力及支护强度是影响底鼓的主要因素。侯朝炯[8]从能量角度提出,挠曲褶皱型底鼓大变形是深部岩体掘进卸荷后岩体弹性能释放的体现,并基于相关数据提出了底板岩体的破坏准则。何满潮[9]、康红普等[10]基于板的挠曲理论解释了底板的大变形机理,并提出了层状底鼓的计算公式。

以上理论从各个角度解释了挠曲褶皱型底板的力学行为,并为底板的变形控制提供了依据。在挠曲褶皱底鼓机理的研究基础上,学者在长期实践中提出了众多底鼓控制方法。高延法等[11]提出了以钢管混凝土作为反底拱的支护方式,在软岩巷道中取得了较好的支护效果。康红普[12]提出了底板注浆并置入底角锚杆的联合支护方式,解决了相关支护难题。杨军等[13]通过室内试验,系统地研究了不同类型的底角锚杆在不同受力状态下的力学性能。此外,“双壳”法[14]、“卸压槽”[15]等卸压技术也有着较为广泛的应用。

本文以鹤岗兴安煤矿四水平18 层南轨道巷为背景,提出了底角钢管混凝土底板桩基支护方式;采用理论分析和数值分析方法分析了挠曲型底鼓底板围岩的破坏特征,提出了底板挠曲失稳判据,研究了高应力下底板桩基的支护机理;通过现场试验验证其支护效果,可为深部矿井底鼓变形控制提供参考。

1 工程概况

兴安煤矿位于鹤岗矿区,煤系地层整体走向呈北东向。构造应力场受第四纪东西向应力场控制,区域地应力场方向近东西向,最大主应力和最小主应力均位于水平面内,中间主应力均位于垂直平面内。该煤矿四水平18 层南轨道巷全长1 165 m,埋深-830 m,掘进尺寸为宽4 900 mm、高4 300 mm,净断面为15.87 m2,如图1所示。该巷道围岩为泥岩、砂质泥岩及中砂岩岩层(表1),底板岩体属于易风化、软化岩体,普氏系数仅为0.21～0.59。现场勘察可知,该巷道底鼓量最大可达1.2 m,底鼓速度可达0.15～0.25 m/d,严重影响了掘进效率。

表1 围岩力学参数Tab.1 Mechanical parameters for coal and rock

图1 巷道断面和支护结构Fig.1 Roadway section and support structure

根据现场地应力测试成果,该巷道所处区域的水平构造应力最大为34.72 MPa,为垂向应力的1.65 倍。该巷道底板围岩处于高水平挤压应力环境中,且底板围岩较为软弱,底板变形属于典型挠曲型底鼓。

2 挠曲型底鼓围岩应力特征

巷道掘进后,巷道围岩应力平衡被破坏,岩体应力重新进行了调整,其计算简图如图2所示。

图2 围岩二次应力计算简图Fig.2 Calculation of secondary stress of surrounding rock

根据弹性力学叠加原理,巷道的弹性应力状态为竖向荷载pz和水平荷载λpz的叠加。围岩应力计算公式[16]如下:

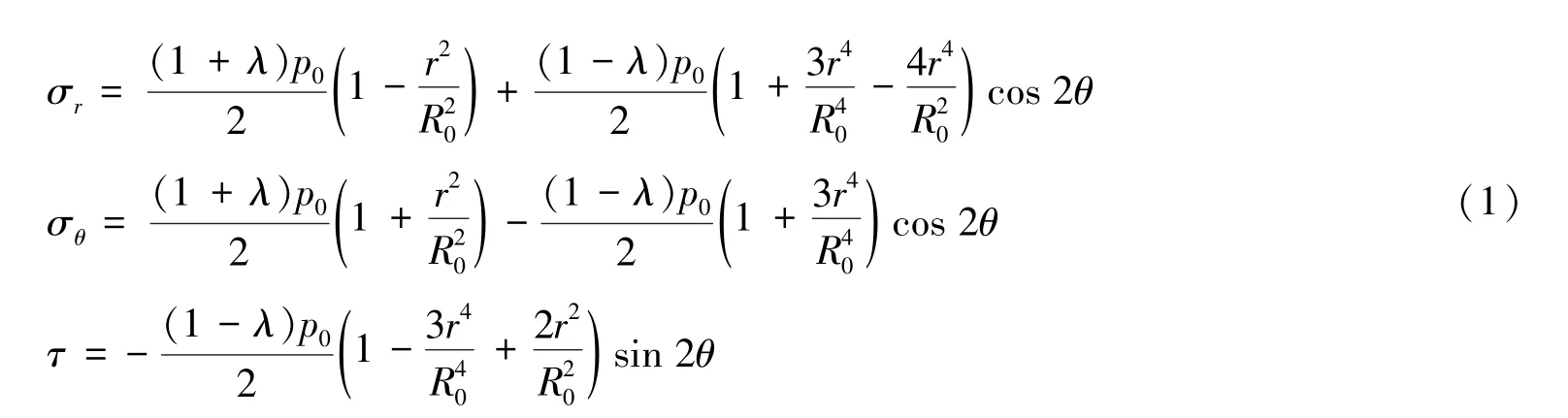
式中,p0为巷道围岩的初始应力;R0为巷道的等效圆半径;σθ为切向应力;σr为径向应力。

显然,当r=R0时,即可求得巷道表面围岩应力,此时径向应力和切应力均为0。根据现场实测,水平应力系数λ=1.65,巷道底板和两帮的切向应力分布如图3所示。底板区域的切向应力集中系数在2.8～3.0,明显高于两帮。应力从底板过渡到两帮后较快衰减,应力集中系数在两帮中心位置衰减至2.35。由于巷道围岩表面的径向应力为0,此时的底板处于二向应力状态下,极易发生挠曲型失稳。

图3 巷道切向应力分布Fig.3 Distribution of tangential stress in roadway

由于底板围岩强度低,切向挤压应力过大导致底板围岩发生了塑性破坏。塑性区不断发展,最终导致底板失稳并发生大变形。根据兴安矿岩体的力学特性,本文采用M-C 准则作为巷道围岩进入塑性区的判据,岩体屈服时微分方程为

由于泥岩进入塑性屈服后会有明显的软化阶段,因此将理想弹塑性模型的残余强度作为常数代入式(2),会使计算结果明显偏小。根据图4 中的底板岩体全应力应变曲线,峰后应力应变曲线可以简化为线性关系,则峰后应力可以表示为

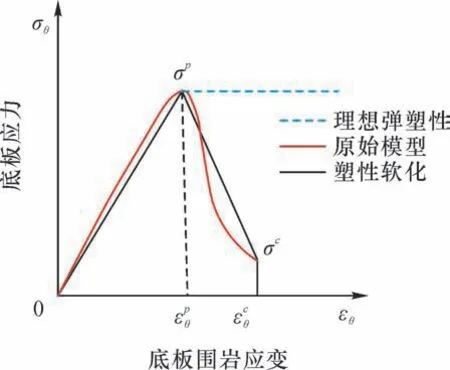
图4 底板岩体全应力-应变曲线Fig.4 Total stress-strain curve of floor rock mass

式中,ν为岩体泊松比;E为岩体弹性模量。

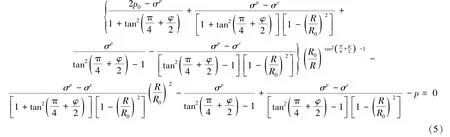
式中,R为巷道塑性区半径;p为巷道的支护反力。

图5 为不同应力环境对塑性区破坏深度影响。由图可知,在不同支护反力下,巷道围岩塑性区半径随初始应力增大呈现近似线性增长的关系。巷道所处位置的地应力越大,围岩塑性区演化越显著。兴安矿四水平轨道所处位置的初始应力为30 MPa 左右,此时对应的塑性区直径为12 m左右,高地应力显著加剧了围岩的变形破坏。通过分析不同强度下塑性区半径可知,增加底板支护反力对巷道高地应力条件下的塑性区发展有一定的抑制作用,当应力水平较低时,底板增加支护强度对塑性区发展的抑制作用不大。当初始应力低于10 MPa 时,0～4 MPa 的支护强度下对应的塑性区半径分别为4.2 m、4.5 m、4.9 m、5.7 m、6.5 m。当地应力超过30 MPa 时,相对于无支护的状态,4 MPa 的支护强度下,塑性区范围可以减少4 m。这表明随着地应力的增大,巷道内底板高强度支护措施可以较好地抑制巷道围岩破坏。然而由于施工条件和支护成本的限制,极少有支护结构能

图5 不同应力环境对塑性区破坏深度影响Fig.5 Influence of different stress environment on the failure depth of plastic zone

图6 为底板塑性区半径与巷道围岩强度参数的曲面关系图。当σp和φ处于较小值时,曲面的曲率明显急剧增大,呈现出“锥尖”形态,塑性区半径的发育近乎指数型增长。当φ和σp分别小于20°和10 MPa 时,巷道的塑性区半径均在10 m 以上且发展极为迅速。随着φ和σp的逐渐增大,曲面的曲率逐渐下降,逐渐退化为平面,对应的塑性区范围发育逐渐平缓。

图6 不同围岩强度参数对塑性深度影响Fig.6 Influence of strength parameters of surrounding rock on plastic depth

与支护强度相比,软弱底板的围岩强度参数对塑性区半径的影响大得多。

综上可知,对于挠曲型底鼓而言,底板围岩应力环境和围岩强度是影响底板变形发展的关键因素。随着巷道塑性区的发育,底板围岩最终发生挠曲型失稳而形成破碎区。破碎区的岩体扩容和塑性变形共同叠加构成了底板大变形。因此,支护时底板桩基必须要阻隔高地应力在底板围岩范围内的传递,对底板围岩进行一定程度加强。

3 底板桩基底鼓控制机理

3.1 底板桩基应力阻隔原理

由上节可知,高应力场下产生的塑性区是由于切向的挤压应力造成的。如图7所示,相对于巷道走向长度y而言,底板的塑性区深度是一个较小的值(R＜＜y),因此底板的大变形问题可以简化为板的弯曲问题进行讨论。

图7 巷道底鼓计算模型Fig.7 Calculation model of floor heave in roadway

由弹性曲面的微分方程[18]可知,巷道底板的挠曲微分方程可以表示为

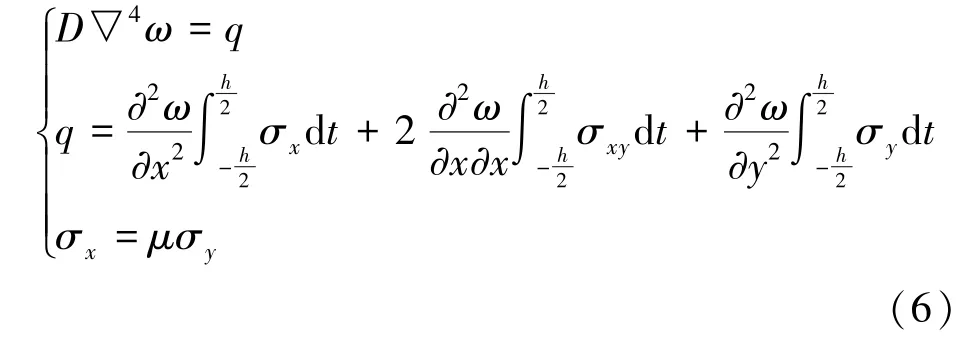
式中,D为底板的弯曲刚度;ω为底板变形;σx为底板的挤压应力;σy为巷道走向的底板正应力;σxy为底板的切应力;t为底板变形计算厚度。

为了求解底板压曲临界状态下的应力,底板变形ω的齐次解采用二维莱维解[19]叠加组成,则ω可以表示为

式中,Am和Bn为待定系数;L为底板横向计算长度;B为底板纵向计算长度。

由于巷道的走向长度y远大于巷道底板宽度x,而且巷道掘进后所受的荷载主要与x方向有关,所以巷道底板的位移、形变和应力都只是与x相关的单值函数,故式(6)和式(7)联立后可以简化为

略去高阶微量,令m=1,代入巷道底板的弯曲刚度,可得底板的挤压应力平衡方程:

解得底板破坏的临界压曲应力:

由上式可知,当巷道底板的塑性区应力超过临界压曲应力时,底板发生了失稳破坏。当r=R0时为最不利的应力环境,此时塑性区失稳的临界条件可以表示为

不难发现,高应力状态下巷道底板的大变形由两部分组成,一部分是巷道进入塑性状态后的变形,一部分是巷道底板发生压曲失稳后的大变形。前者与岩体参数有关,并且随时间的推移缓慢增大;后者属于底板围岩的整体失稳变形破坏,具有变形量大、发展迅速的特点。

针对该类型的底鼓形式,底板桩基的结构形式可以较好提供应力阻隔效果,如图8所示。总体来说,底板桩基的施工工法分为3 个步骤:

图8 底板桩基支护模型Fig.8 Support model of floor corner pile

(1)卸压。在底板底角部位进行大直径钻孔卸压。卸压完成后,将一定规格的钢管在底板底角部位钻孔置入至巷道的硬岩区域,达到一定嵌固距离后,可以视作固定约束。

(2)注浆。通过钢管进行注浆,浆液通过钢管的预留孔洞进入岩体裂隙。注浆一方面可以提高底板围岩的变形模量和强度参数,减少围岩自身的塑性变形;另一方面可以将钢管与周边围岩粘结在一起协同受力,从而形成受力共同体。

(3)成桩。注浆完成后向钢管内灌注自密实混凝土,形成钢管混凝土结构,从而将底板的水平挤压应力传递到原岩应力区,降低底板围岩应力,起到较好的应力阻隔效果。

3.2 底板桩基阻隔应力分析

底板桩基施工后,由于底板桩基的应力阻隔作用,塑性区压曲失稳的临界判据可以表示为

式中,σ*为底板桩基提供的阻隔应力,即能承受最大的挤压应力σx。

此时底板围岩应力路径如图9所示。巷道掘进后,底板应力达到临界应力(C点)时,底板发生挠曲破坏。当采取增大底板支护强度后,底板应力增长至临界应力D点时继续发生挠曲破坏。因此,高应力环境下,相对增大支护强度、释放和转移底板应力,是防止底板发生挠曲破坏的有效措施。当底角的大直径钻孔卸压后,底板应力由A点下降至B。注浆提升了围岩的力学参数,此时围岩的二次加载曲线斜率明显变大。底板桩成桩后,由于围岩与钢管混凝土协同受力,此时围岩应力应变曲线接近理想弹塑性模型,峰后应力趋于常数。该常数与底板临界应力的差值,即为底板桩基的阻隔应力。

图9 支护状态下底板应力路径Fig.9 Floor stress path under support

由于底板桩基一端嵌入到原岩应力区,可以视为固定约束;一端固定在巷道底角部位,由于底板围岩此时进入了塑性区,可以产生较大的变形,但仍可以约束其转角,因此可以简化为滑动支座。底板桩基的结构计算模型如图10所示,b为底板桩基的桩间距。

图10 底板桩基内力计算模型Fig.10 Internal force calculation model of floor corner pile

钢管混凝土包裹在水泥浆液强化后的注浆体内,在围压的作用下可以体现出较好的延性。考虑钢管混凝土的屈曲后强度,通过塑性设计的方法计算求得的阻隔应力可以较好地反映钢管的实际受力状态。由结构的塑性设计理论可知,结构中的某些局部截面达到极限弯矩时会出现塑性铰,当足够多塑性铰出现时,原结构会失去承载能力,此时钢管混凝土所对应的极限荷载即为极限阻隔应力σ*。根据底板桩基的约束受力条件,塑性铰出现的位置如图11所示。

图11 底板桩基极限荷载计算模型Fig.11 Calculation model of ultimate load of floor corner pile

由虚功原理[20]可知,外力所做虚功等于内力在相应虚变形上所做虚功。设约束位置处的虚位移为θ,则由几何关系可知,跨中处的虚位移为2θ,故外力虚功为

内力虚功为

令We=Wi,则极限荷载和阻隔应力的关系为

由于钢管被C40 自密实混凝土灌注,根据《钢管混凝土结构技术规范》,钢管混凝土构件的受弯承载力可以简化为下式:

式中,θ为钢管混凝土的套箍系数;asc为截面含钢率;f为钢管钢材抗拉强度;r0为等效圆半径,当采用圆钢管时即为等效半径;fsc为钢管混凝土的抗压强度设计值。

联立式(15)和式(16)可以得到底板桩基的极限阻隔应力:

对软弱岩层,注浆后底板围岩黏聚力c为7 MPa,内摩擦角为30°,可知此时塑性区半径R0为6.45 m,塑性区应力为12.15 MPa,底板此时的临界压曲压力为8.35 MPa。由于塑性区应力大于临界压曲应力,此时底板会发生失稳破坏。为了研究不同桩间距和桩径对极限阻隔应力的影响,在上述参数的基础上,以常用的12 mm 壁厚钢管为例进行试验。

如图12所示,极限阻隔应力随着钢管混凝土的半径增大而逐渐增大。当桩径在80 mm 以下时,极限阻隔应力随底板桩基等效半径呈现类似线性增长的趋势,此时极限反力的增长幅度不太明显;当桩径超过80 mm 时,极限阻隔应力的增长明显加快,并呈现出明显的三次曲线形式。这是由于底板桩在挤压应力的作用下,受力状态主要以受弯为主,当桩体材料确定时,桩径的增大对底板的抗弯刚度起着决定性的作用。

图12 支护参数对阻隔应力的影响Fig.12 Influence of support parameters on barrier stress

桩间距对阻隔应力的增大也有明显的影响。当桩间距大于1 200 mm 时,底板桩基所能提供的阻隔应力不超过1.5 MPa;当桩间距大于1 200 mm时,极限阻隔应力的明显增大。在同一桩径下,300 mm 和600 mm 的桩间距下最大可以相差4 MPa。一方面是由于阻隔应力与桩间距成反比,另一方面是桩间距过大时,每根桩分担的受力区域较大,导致了应力的阻隔效果不明显。

4 底板桩基底鼓控制效果分析

4.1 数值模型的建立

由于底板桩基的桩长和施工角度通过理论分析较难得到解析解,为了研究底板桩基设计参数对支护效果的影响,采用FLAC3D数值模型对底板应力阻隔效果和变形进行分析。模型参数以兴安矿四水平南18 层轨道巷为基础,根据巷道应力的影响范围[21-23],模型的尺寸为200 m× 120 m×100 m,模型底部固定了XYZ方向的位移,顶部施加竖直方向的应力模拟上覆岩层的地应力,四周约束施加水平应力边界条件,水平应力初始值34.72 MPa,水平应力梯度为35.1 kN/m3。计算模型如图13所示,巷道围岩力学参数见表1。

图13 数值计算模型Fig.13 Numerical calculation model

表2 围岩力学参数Tab.2 Mechanical parameters for surrounding rock

理论分析中假定底板岩体各向同性且滑移区处于朗肯极限状态,因此围岩模拟采取Mohr-Coulmb 模型。由于底板桩基具有较大的支护刚度和较好的抗弯剪性能,因此桩基模拟采用Pile 结构单元,并打开锚杆特性,以较好地实现其与围岩共同承载特性。桩截面直径为200 mm,桩间距为600 mm。巷道U 型钢支架采用shell 单元进行模拟,间距为800 mm。结构单元空间布置如图14所示。

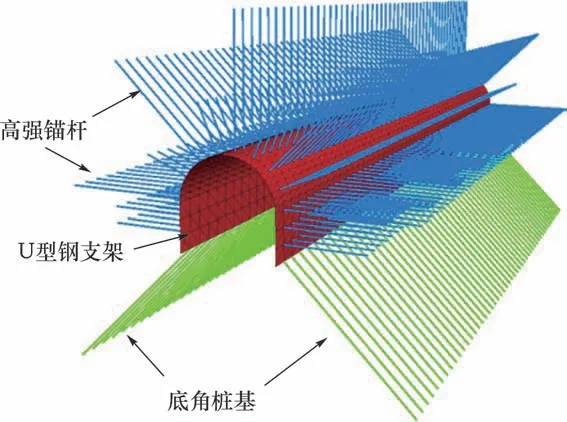
图14 结构单元模型Fig.14 Structural element model

4.2 不同桩长支护效果分析

为了分析不同桩长对巷道底板支护效果的影响,模拟了底板无支护和底角桩长分别为6.5 m、7.8 m、9.1 m、10.4 m 的支护工况,不同桩长分别对应着0、1.2R、1.4R、1.6R(R为塑性区半径)的嵌固长度,钻孔角度默认为45°。如图15所示,巷道的底鼓形状在不同支护条件下均表现为两底角底鼓量小,中部底鼓量大,呈现为抛物线型,这是由于底板两端的岩体被两帮岩体所约束,而中间岩体为无约束的临空面。当嵌固深度为0.2R时,巷道最大底鼓量为820 mm,与无支护条件下的底板变形非常接近;当嵌固深度为0.4R时,与未支护状态下对比,巷道最大底鼓量减少了820 mm;当嵌固深度为0.6R时,巷道底鼓量略有减小,但减小程度不明显。这是由于0.6R的嵌固深度已经完全实现了底板桩在深部岩体的固定约束,当桩长继续增大时,极限阻隔应力由桩体的材料参数决定。

图15 不同桩长下的底鼓Fig.15 Magnitude of floor heave under different pile lengths

综上所述,桩长为0.4R～0.6R嵌固深度时,支护效果最佳。

4.3 不同角度支护效果分析

不同支护角度下的巷道底鼓量如图16所示。该支护角度指的是底角桩与竖直方向所呈的夹角。由于底板桩基的计算模型是极坐标中建立的,因此底板桩应在巷道截面形心与巷道底角的连线上,如图17所示,该连线即为巷道等效圆的半径方向,该角度即为底板桩基的理论计算角度。

图17 底板桩基钻孔施工角度Fig.17 Drilling angles of floor corner pile

由图16 可知,当底板桩基支护角度与竖直方向夹角为35°时,巷道底鼓量最小,为170 mm 左右。该角度与理论值34°较为接近。当桩基支护与竖直方向夹角大于35°时,巷道底鼓量明显增大。这是由于,此时的底板桩基钻孔已经偏移了等效圆的直径方向,底板围岩的切向正应力主要分解成了底板桩基的轴向拉拔力,使其与围岩脱离,最终较难达到应力阻隔效果。当底角桩支护角度小于35°时,底鼓变形量比较接近。这是由于此时底板围岩的径向应力接近水平方向分布,这使得钢管混凝土桩受力以弯曲为主,从而较好地发挥了钢管混凝土的抗弯能力,起到了应力阻隔的作用。因此,当现场条件无法满足底角桩的设计角度时,宜在底角部位垂直于底板钻孔。

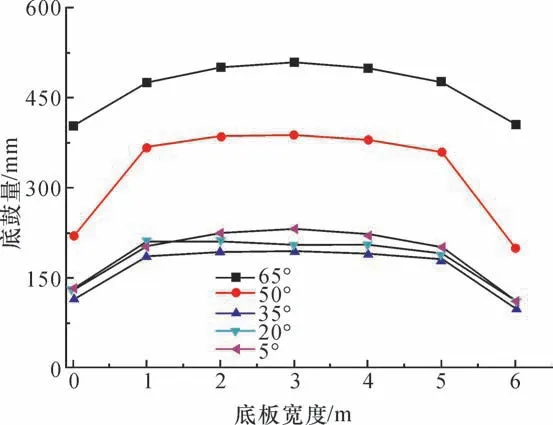
图16 不同钻孔角度下的底鼓Fig.16 Floor heave under different borehole angles

4.4 巷道底板应力分析

为了分析底板桩基的应力阻隔效果,对数值模型中巷道底板临空面围岩及X轴同一水平面内的岩体进行了应力监测,并基于映射规则[24-25]在MATLAB 软件中换算为圆形巷道中的切向应力,如图18所示。由于巷道开掘后底板围岩临空且处于二维应力状态,因此在同一支护条件下,底板应力基本不随X坐标变化。当底板采用底板桩基支护后,巷道底板围岩应力由12 MPa 降至7.5 MPa,通过计算可知,支护后的底板应力小于极限应力,不会发生失稳大变形。巷道外侧的底板围岩塑性区应力有所下降,但下降程度有所衰减,进入弹性及初始应力区后,应力阻隔效果继续衰减。表明底板桩基可以有效阻隔塑性区应力向底板围岩处的传递,其阻隔效果随着远离巷道而逐渐衰减。

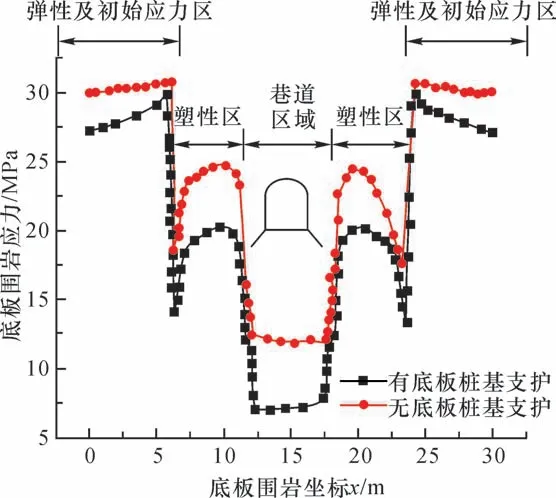
图18 底板围岩应力分布Fig.18 Stress distribution of floor surrounding rock

5 现场工程应用

5.1 现场试验概况

现场试验位置选取兴安煤矿四水平南18 层轨道掘进巷道5 号测点以南23～123 m 范围。其中,试验区段为23～73 m,该段进行了底板桩基支护;73～123 m 为对照区段,该段底板不进行处理(图19)。为了研究底板桩基的支护效果,现场通过十字布点法监测巷道表面位移,布点位置为对照区段与试验区段中部。

图19 底板桩基现场布置Fig.19 Site layout of floor corner pile

根据室内试验结果、兴安煤矿地质条件和文中的计算公式,确定了支护参数,提出了底板治理方案及总体施工工艺,即底角钻孔→底板深部注浆→底板桩基施工。其中,底角钻孔直径为200 mm,深度为10 m,竖直方向外摆35°,底板桩基间距为400 mm。在钻孔过程中,如发生塌孔或难以成孔,应下注浆管,进行预注浆,待巷道围岩稳定后再施工,直至成孔。当钻孔施工完毕后,在钻孔中插入外径194 mm、壁厚12 mm 的钢管,钢管屈服强度为300 MPa。注浆材料为超细水泥浆液,水灰比为2∶1,注浆压力为2.5 MPa,当管壁与钻孔之间充满浆液时停止注浆。注浆完毕后,利用混凝土泵向钢管中灌注混凝土。混凝土强度等级为C40,水、水泥、砂、石基准配比为0.38∶1∶3.6∶5.4。

5.2 现场试验结果分析

巷道试验区段及对照区段的巷道变形见表3。由表可知,未进行底板桩基支护的对照区段,巷道围岩在水平应力的作用下变形较为剧烈。巷道底鼓量100 cm,两帮缩进量为90 cm 左右,需进行扩容方能正常使用。试验区段采用桩基对底板进行处理,与对照段相比,巷道底鼓变形量稳定值由100 cm 下降至35 cm,两帮缩进稳定基本保持不变,可以满足巷道的正常使用。这表明在高水平应力作用下的巷道中,底板桩基可以较好地控制巷道底板的变形。

表3 巷道围岩最大变形统计Tab.3 Maximum deformation statistics of roadway surrounding rock

6 结论

(1)挠曲型底鼓机理是底板挤压应力超过了临界力导致围岩压曲失稳。高应力环境下底板围岩强度不足是引发巷道底板失稳的主要原因,改善底板围岩应力环境和强化底板围岩是治理挠曲型底鼓的关键。

(2)提出了底板桩基应力阻隔力学模型,推导出了底板桩基支护状态下底板围岩压曲失稳的临界判据。结合钢管混凝土的抗弯特性和虚功原理,推导出了底板桩基的极限阻隔抗力表达式。底板桩基的截面几何参数和桩间距是决定极限阻隔抗力的关键参数。

(3)通过建立数值模型,分析了底板桩长和钻孔角度对底板变形控制的影响。结果表明,桩长宜采用0.4R～0.6R(R为底板塑性区半径)嵌固深度,底板桩基布设应通过巷道截面等效圆半径或偏向垂直方向。底板桩基应力对巷道底板围岩的挤压应力有较好的阻隔效果。

(4)现场采用钻孔+注浆+成桩一体化施工,可以较好地强化围岩力学参数、改善底板围岩应力环境。监测数据表明,底板桩基可以较好地控制底板及两帮变形,使巷道的稳定性显著提高。该技术为类似巷道底鼓变形支护方案提供了参考。