膏体充填开采覆岩移动变形规律研究
廖宝泉, 柯愈贤, 方立发, 胡凯建*, 曾杰, 陶铁军,2
(1.江西理工大学资源与环境工程学院,江西 赣州 341000;2.贵州大学土木工程学院,贵阳 550025)
随着矿山行业的不断发展,膏体充填开采技术由于可有效解决采空区塌陷的安全问题,在地下开采矿山中运用越来越广泛[1-3]。充填开采下覆岩的移动变形特征是衡量充填控制围岩变形效果的重要直接参数[4-6],探明其变化规律能够为合理设计充填方案提供有效的理论指导,保障矿山的生产安全[7-9]。
近年来,不少学者对充填开采中覆岩的移动变形特征进行了研究。常庆粮等研究分析了不同影响因素下充填开采覆岩移动变形特征,建立了充填开采岩层移动的力学模型[10]。杨宝贵等研究分析了充填开采不同充填率和充填体强度对覆岩移动变形的控制效果[11]。贾林刚等分别采用相似模拟试验和数值模拟计算,研究分析了不同充填率下的覆岩变形破坏特征,确定了覆岩移动变形和充填率间的关系[12-13]。王磊等研究分析了充填开采覆岩形态和移动变化规律,建立了充填开采地表沉陷模型[14]。郎博等研究分析了不同充填率条件下单工作面和多工作面内的覆岩移动变形规律[15]。郭庆彪等基于连续—离散介质耦合思想,建立了充填开采后的沉陷预测模型[16]。江飞飞等通过理论分析与数据观测相结合的方法,分析评价了充填开采下地表移动特征及矿山现状[17]。以上研究均表明充填开采法能够有效控制覆岩的移动与变形,完善了充填理论体系,促进了充填技术的进步,但以上研究主要集中在对覆岩移动变形影响因素分析和地表移动变形预测等方面,未见关于充填开采覆岩移动角变化规律方面的研究。
移动角是研究岩层移动与变形的重要角值参数,用于圈定地下开采工程中的岩层移动范围[18-19]。然而由于充填开采下覆岩移动角变化规律尚不明确,在采用充填开采技术进行地下开采时,矿山仍使用传统方法来确定覆岩的移动角,并以此圈定地表移动范围,往往导致圈定的地表移动范围过大,从而造成开采成本高、资源浪费严重等问题[20-21]。鉴于此,本文采用数值模拟计算方法,建立数值计算模型,基于充填开采不同影响因素下覆岩的移动变形特征,分析覆岩不同水平的移动与变形规律,进而确定覆岩不同水平的移动角及其变化规律,为矿山充填开采下覆岩移动角的合理确定提供一定参考。
1 计算模型及模拟方案设计
1.1 计算模型的建立
以某矿山的工作剖面为原型,采用FLAC3D有限差分软件建立平面计算模型。根据该矿山地质勘探资料可知,矿体埋深约为200 m,平均厚度为5 m,矿体及其上下盘岩层呈近水平分布。为简便计算与分析,各岩层按水平分布处理,同时对其进行合并简化,模型具体如图1所示,其中模型水平方向长度为600 m、垂直方向高度250 m,矿体埋深200 m,充填开采区域为矿体水平方向上的200~400 m。

图1 数值计算模型Fig.1 Numerical calculation model
模型所涉及岩体均为弹塑性材料,故本构关系采用摩尔—库仑屈服准则。矿体和围岩的力学参数见表1所列。

表1 岩体力学参数Table 1 Mechanical parameters of rock
模型施加的边界条件如下:对模型X方向两侧边界进行水平位移约束;对模型中所有节点的Y方向位移进行约束,以实现平面应变分析;约束底部边界的全部位移,使其为固定边界,顶部边界则为自由面。
1.2 数值模拟方案
本模拟旨在研究充填开采下覆岩的移动变形特征及移动角变化规律。根据充填开采工艺流程及现有研究[22-23]可知,充填开采下覆岩的移动变形受开采深度、矿体倾角、充填率、充填体力学性质等多因素影响,其中充填率和充填体力学性质对其影响较大。因此,本文选择在不同充填率和不同充填体力学性质条件下进行充填开采模拟。
通过改变充填体的灰砂质量比(即水泥与全尾砂的质量比,下同)以获得不同充填体力学性质,设计4种灰砂质量比,分别为1∶4、1∶8、1∶10、1∶12,通过室内试验测得养护龄期为28天的不同灰砂质量比的充填体力学参数,结果见表2所列。考虑到开采厚度及矿山实际充填状况,设计了2种充填率,分别为90%、100%,共需要进行8组数值模拟计算。
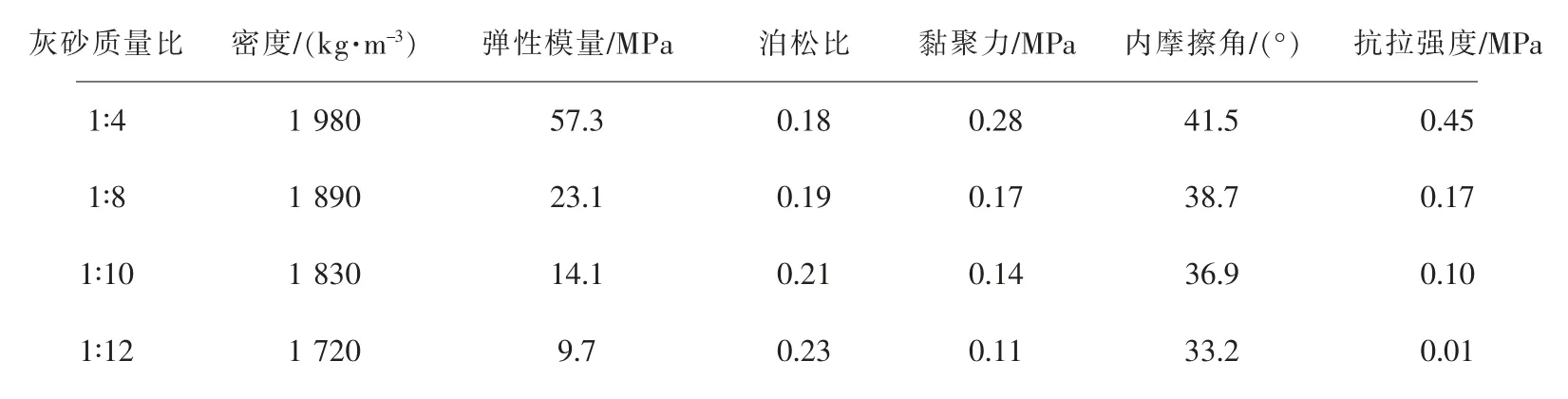
表2 充填体力学参数Table 2 Mechanical parameters of the filler
2 计算结果分析
2.1 地表沉降规律分析
地表沉陷规律对控制地面下沉、保障矿山生产着充填体灰砂质量比的增大,地表下沉量不断减小,而当充填率增加时,地表下沉量同样减小,且下沉曲线更趋于平缓。这主要是由于充填体力学性质越强,充填体对覆岩的支撑能力越好,使得覆岩的沉降减小;而充填率越高,顶板与充填体间的距离越小,顶板的垮落高度相对越低,覆岩的沉降也会越小。当充填率为90%时,采用灰砂质量比1∶12的充填体进行充填,地表下沉最大值为533 mm,采用灰砂质量比1∶4的充填体进行充填,下沉最大值则为407 mm,相较安全以及确定地表移动范围有着重要意义。充填率为90%和100%时,不同灰砂质量比下的地表下沉曲线分别如图2、图3所示。
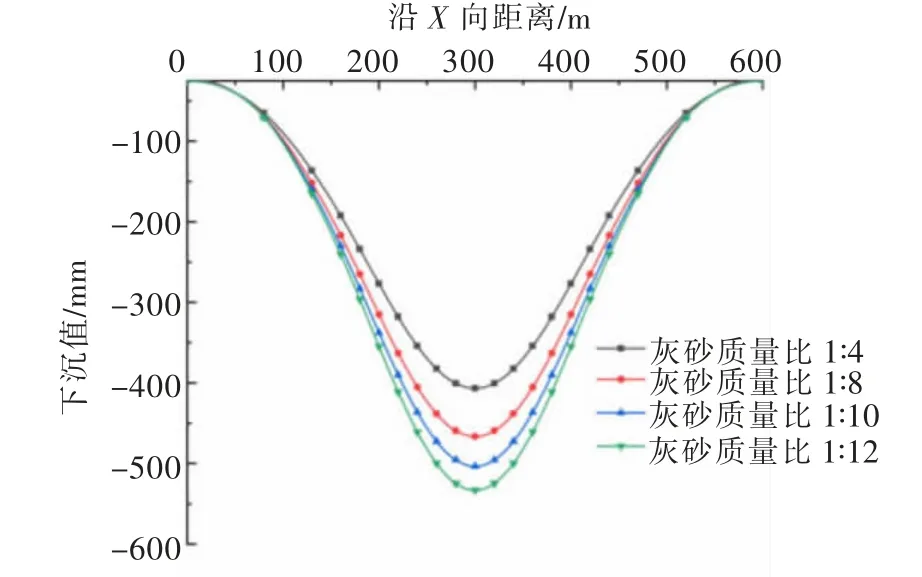
图2 充填率90%时的地表下沉曲线Fig.2 Surface subsidence curve at 90%filling rate
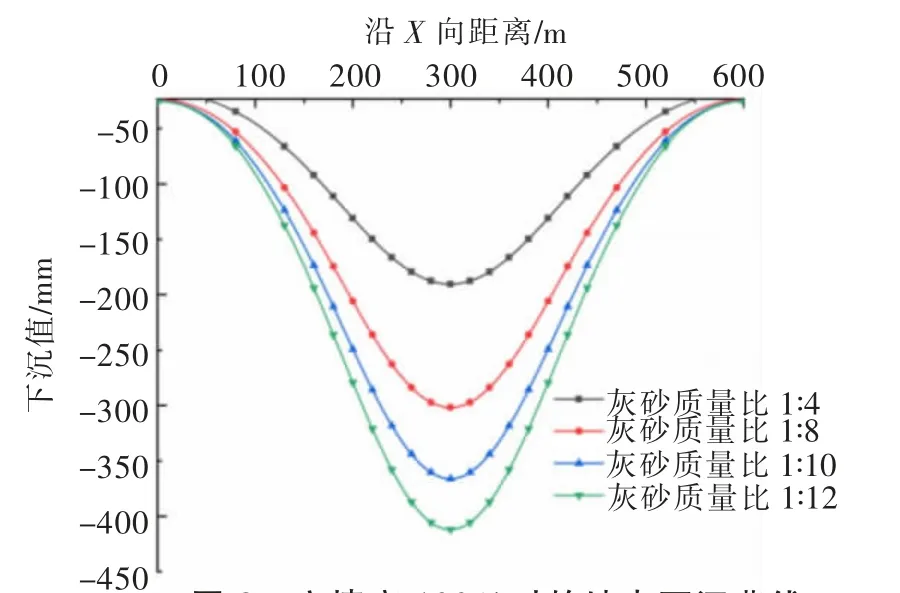
图3 充填率100%时的地表下沉曲线Fig.3 Surface subsidence curve at 100%filling rate
由图2、图3可看出,充填开采地表下沉曲线规律明显,呈对称分布,在中轴线处达到下沉极值。随于充填体灰砂质量比为1∶12情况下的下沉最大值,减小了23.6%;而当充填率为100%时,充填体灰砂质量比为1∶12情况下的下沉最大值为412 mm,灰砂质量比为1∶4情况下的下沉最大值为190 mm,下沉最大值减小了53.9%,降低程度要高于充填率为90%时。综合上述分析,提高充填率和增强充填体力学性质均可有效减小地表下沉量,且在充填率较高的情况下,通过增强充填体力学性质来降低地表下沉的效果会优于充填率较低的情况。
2.2 覆岩变形规律分析
覆岩的变形特征是合理确定覆岩移动角的基础,表征覆岩变形特征的主要指标为倾斜、曲率、水平变形。根据规范[24],以倾斜值3 mm/m、曲率值0.2 mm/m2、水平变形值2 mm/m这3个临界变形值作为求取覆岩不同水平移动角的标准。因此,在计算模型内各水平高度上每2 m取一个分段,采用FLAC3D内嵌的Fish语言编程,获取覆岩不同水平高度上不同分段的变形值,从而确定覆岩不同水平的变形特征。
由于经计算得出的覆岩各水平高度上的曲率极值和水平变形极值相比于临界变形值较小,对确定覆岩不同水平移动角的影响可忽略不计,故主要针对覆岩不同水平的倾斜值进行分析。基于所求取的覆岩不同水平的倾斜值,运用Sufer绘图软件,绘制充填率为90%和100%时不同充填体灰砂质量比下的覆岩倾斜变形等值线,如图4、图5所示。
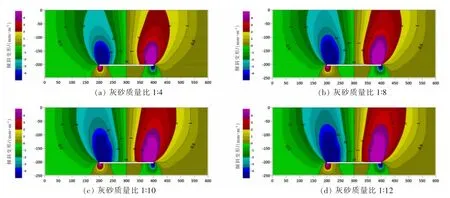
图4 充填率90%时不同灰砂质量比下的倾斜变形等值线Fig.4 Inclination contours for different mass ratio of cement-sand at 90%filling rate

图5 充填率100%时不同灰砂质量比下的倾斜变形等值线Fig.5 Inclination contours for different mass ratio of cement-sand at 100%filling rate
由图4、图5可看出,在充填率为100%和90%的情况下,以不同灰砂质量比的充填体进行充填,覆岩倾斜为临界变形值3 mm/m的等值线均未发育至地表,表明膏体充填开采技术可以有效控制覆岩变形,使地表未出现危险变形区(倾斜值i≥3 mm/m的区域),从而保障矿山的地表建筑安全。但随着充填体灰砂质量比的减小,不仅覆岩各水平高度上的倾斜极值会随之增大,覆岩危险变形区的发育高度,即危险变形区最高点距顶板的高度也会随之增大。充填率为90%时,以灰砂质量比为1∶4的充填体进行充填,危险变形区的发育高度为106.6 m,而以灰砂质量比为1∶12的充填体进行充填,其发育高度则迅速增长为191.1 m,已经接近地表。这正是由于充填体灰砂质量比减小时,其致密性变差,强度降低,使得充填体抵抗上盘岩层荷载能力也随之减小,从而无法有效地阻止岩层的破坏变形向上传播,使得水平高度较高处覆岩出现危险变形区。
对比图4、图5可发现,提高充填率可明显降低危险变形区的发育高度,且降低程度相比于随灰砂质量比增大而降低的程度要大。其中,充填率为100%时,以灰砂质量比为1∶12的充填体进行充填,危险变形区的发育高度为107.6 m,与充填率为90%时,以1∶4的充填体进行充填的情况相近。这是因为提高充填率可减小充填体欠接顶量,进而减小顶板的移动变形,而增大充填体灰砂质量比只是对充填体自身承载能力的增强,限制了顶板在与充填体接触后的移动变形。因此,矿山在实际充填开采过程中,需在选定合适的充填率的基础上对充填体灰砂质量比进行选择,从而在保证安全生产的前提下,合理地控制充填成本。
为进一步分析不同充填体灰砂质量比对危险变形区发育高度的影响,以充填率90%为例,对不同充填体灰砂质量比下覆岩危险变形区的发育高度进行回归分析,得到二者间的关系曲线,如图6所示,回归方程为:

图6 灰砂质量比与覆岩危险变形区发育高度的关系曲线Fig.6 Relationship between mass ratio of cement-sand and height of development of hazardous deformation zone
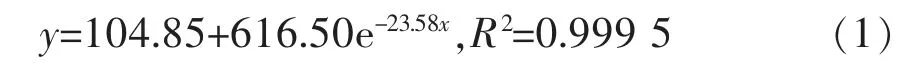
式(1)中:y为覆岩危险变形区的发育高度;x为充填体灰砂质量比。
通过图6和式(1)可发现,覆岩危险变形区发育高度离散点与拟合曲线的相关性较好,表明充填开采中覆岩倾斜临界值的发育高度与灰砂质量比之间存在指数函数关系。当充填体灰砂质量比减小时,危险变形区的发育高度将随之增大,并逐渐发育至地表,威胁到地面建筑的安全。而当灰砂质量比增大到一定程度,曲线趋于平缓,这时继续增大充填体灰砂质量比对降低覆岩危险变形区的发育高度已无太大作用。
2.3 覆岩移动角变化规律分析
依据覆岩不同水平的变形值求取不同水平高度上的覆岩移动角,得到充填率为90%和100%时不同充填体灰砂质量比下的覆岩移动角曲线图,如图7、图8所示。
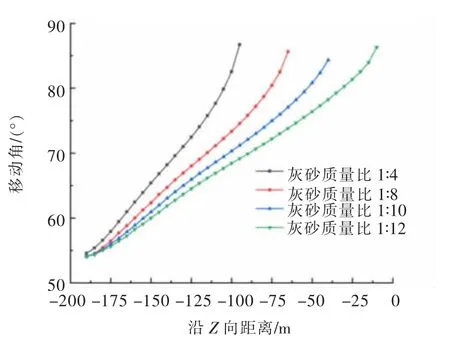
图7 充填率90%时覆岩不同水平移动角Fig.7 Strata displacement angle at 90%filling rate
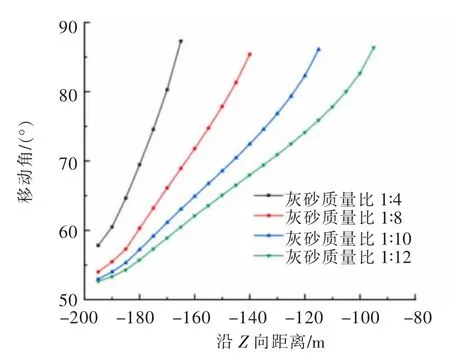
图8 充填率100%时覆岩不同水平移动角Fig.8 Strata displacement angle at 100%filling rate
由图7、图8可看出,覆岩移动角随着覆岩水平高度的升高而不断增大,即水平高度较高处覆岩的移动角要大于水平高度较低处覆岩的移动角。而不同灰砂质量比下同水平的覆岩移动角则会随着灰砂质量比的增大而增大,在充填率为90%时,以灰砂质量比1∶8的充填体进行充填的情况下,-150 m水平的覆岩移动角为62.4°,-100 m水平的覆岩移动角为73.4°;而以灰砂质量比1∶10的充填体进行充填的情况下,-150 m水平的移动角为60.9°,-100 m为70.3°,由此可确定,当充填体灰砂质量比较大时,随着覆岩高度的升高,其移动角的增大程度较大。同时由于提高充填率能够有效阻止覆岩变形的发育,使得同水平高度下覆岩危险变形区的边界与开采边界线之间的距离减小,因此,相同灰砂质量比下充填率为100%时的覆岩移动角要大于充填率90%时,且覆岩移动角随覆岩高度升高而增大的幅度也更为明显。
为进一步研究覆岩不同水平移动角的变化规律。在充填率90%以灰砂质量比1∶4的充填体进行充填的情况下,对距顶板不同高度下的覆岩移动角进行回归分析,关系曲线如图9所示,回归方程为:
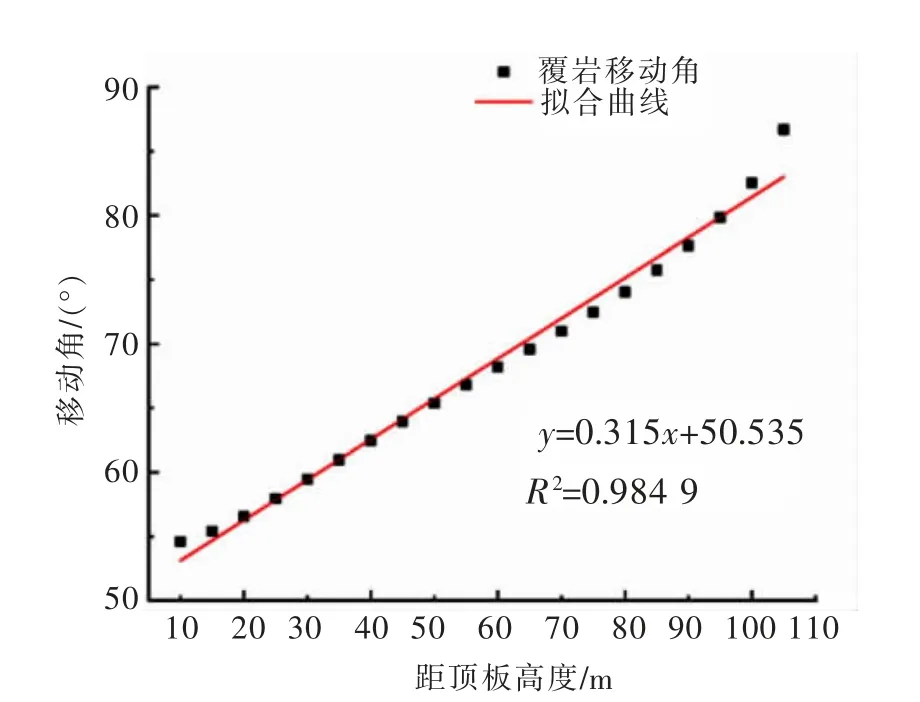
图9 覆岩距顶板高度与移动角的关系曲线Fig.9 Relationship between the height of strata from roof and the displacement angle

式(2)中:y为覆岩移动角,且y≤90°;x为覆岩距顶板高度。
由图9和式(2)可知,拟合相关系数为0.984 9,表明覆岩移动角与覆岩距顶板高度间满足良好的线性关系,当覆岩距顶板的高度增大时,覆岩移动角会随之线性增大。同时对充填率90%以灰砂质量比1∶8、1∶10、1∶12的充填体进行充填时,不同高度下的覆岩移动角分别进行回归分析,回归方程见表3所列。
对比表3中各公式可发现,线性方程的截距a基本相等,均在51°左右,对方程斜率b与充填体灰砂质量比n进行回归分析,得出二者间的关系式为:
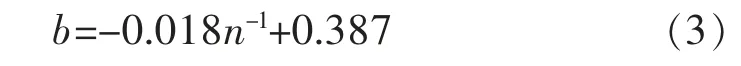

表3 不同灰砂质量比下距顶板不同高度处覆岩移动角的回归方程Table 3 Equations of displacement angle at different heights from roof under different mass ratio of cement-sand
式(3)中:b为方程斜率;n为充填体灰砂质量比。
由此可得出该矿山在充填率为90%时,不同充填体灰砂质量比影响下覆岩移动角随覆岩距顶板高度变化而变化的关系式:
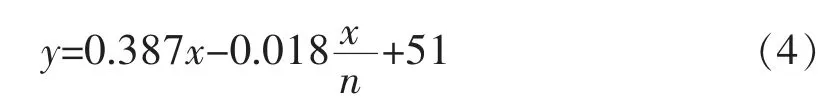
式(4)中:y为覆岩移动角;x为覆岩距顶板高度;n为充填体灰砂质量比。
通过式(4)可确定覆岩移动角在不同充填体灰砂质量比影响下覆岩移动角与覆岩距离顶板的高度之间的变化规律,并基于此式对矿山膏体充填开采下覆岩不同水平的移动角进行预测,从而合理确定矿山地表移动范围。
3 结 论
1)通过对不同充填体灰砂质量比和不同充填率影响下的地表移动进行模拟,发现随着充填体灰砂质量比的增大,地表下沉程度降低。同时在较高充填率下,地表下沉随灰砂质量比增大而降低的程度会更好。
2)根据某矿山充填开采下的覆岩倾斜变形等值线,确定该矿山地面未出现危险变形区,处于安全状态,并得出了覆岩危险变形区的发育高度会随着充填率和充填体灰砂质量比的增大而减小的变化规律。同时通过曲线拟合,发现危险变形区的发育高度与充填体灰砂质量比之间存在指数函数关系。
3)基于模拟结果,经计算得出膏体充填开采下覆岩移动角会随着覆岩水平高度的升高而逐渐增大,且增大充填体灰砂质量比和提高充填率会使得其增大程度变高。结合回归分析,发现覆岩移动角与覆岩距顶板高度之间为线性关系,并建立了覆岩距顶板高度、充填体灰砂质量比与覆岩移动角之间的关系式,进一步揭示了膏体充填开采覆岩移动角的变化规律。

