矿区开采过程中覆岩移动规律数值模拟研究*
刘赟,王创业
(内蒙古科技大学, 内蒙古 包头市 014010)
0 引言
按照中国地质调查局《地质图空间数据库建设工作指南》、《数字地质空间数据库标准(2006)》的要求,基于矿山开采的地质矿产勘探主要对以往工作中新发现的含矿层、矿化蚀变带、矿带和其他重要找矿线索,进行了全面的概略检查。由于矿产资源已经被大力开采,地质矿产勘查主要针对植被覆盖严重的区域,同时在矿区开采过程中,必须考虑矿产资源的特殊性以及复杂性[1]。从理论计算上来讲,由于覆岩移动的客观存在,导致保证覆岩岩石强度、弹性模量均较高的厚关键承载层的黏结力退化,应力逐渐均匀化。当覆岩呈现双向应力状态时,覆岩移动规律必然会随着另一向应力的增加而发生变化。在明确覆岩移动规律的基础上,增加覆岩的截面高度、纵向受力强度等级或面积以及岩性强度等级,在一定程度上对覆岩移动规律数值模拟是有利的。在矿区开采过程中发生覆岩移动应力应变时,采用采动覆岩竖向应变及水平应变模拟相结合的模拟方法可保证模拟的精度。在一定程度上,明确覆岩移动规律对提高矿区开采过程的安全性是有利的。因此,对覆岩层移动规律的研究具有重要的现实意义,能够为矿井生产以及矿区安全开采提供理论指导和借鉴作用[2-3]。
1 矿区开采过程中覆岩移动规律数值模拟
由于覆岩移动过程中外界环境是相对稳定的,所以覆岩移动规律并不随着时间的变化而变化。因此,覆岩移动的数值模拟过程是一个稳态模拟的过程,数值模拟流程如图1所示。

图1 数据模拟流程
本文重点针对覆岩移动规律数值模型、约束条件以及数值模拟结果进行重点阐述。
1.1 建立数值模型
根据工作面的倾向长度所对应的应变值,结合地表岩移观测结果,计算覆岩在自重应力作用下的蠕变公式。设覆岩的蠕变为ε(t),其计算公式见式(1)。

式中,x为覆岩移动黏滞性系数;r1为弹性模量。
由于覆岩移动是三维的,采用三维分析单元SOGFGD80,以x、y、z这3个方向进行覆岩移动规律的特征数据传递。SOGFGD80主要应用于三维动态的仿真模拟,该单元能实现覆岩移动规律数据的传递。基于 SOGFGD80将得出的覆岩蠕变公式代入静力平衡条件,可得覆岩移动规律数值模拟模型M:

式中,b为覆岩移动变形值;β为覆岩垂直方向位移;f为覆岩水平方向位移;σ为水平应力。
由于覆岩岩层弹性模量低,因此在模拟过程中必须考虑覆岩受压屈服造成破坏的情况[4]。通过覆岩移动规律数值模拟模型,模拟覆岩的屈服强度以及采空区支承压力平均值,得出类似于正截面承载力中的覆岩破坏。由于覆岩移动的客观存在,模型网格划分时很容易出现波动现象,导致模拟结果出现明显的脆性。因此,下一步为保证模型的稳定性,针对覆岩移动规律数值模拟边界条件进行定义。
1.2 定义边界条件
从理论上来讲,必须遵循覆岩移动规律对数值模拟边界条件进行定义[5]。通过覆岩移动规律进行数据集的反演研究,得到了一些宝贵的经验。覆岩移动规律数值模拟的整个计算过程,均是以覆岩在自重应力作用下产生位移的假定作为基础,也就是说覆岩移动各点应变与中和轴的距离必须为正比例,覆岩层移动变形与外围相应处的应变一致,将模型的顶部边界作为自由边界,并约束周边的水平位移,由此形成模型底部的全约束边界,以符合覆岩移动规律数值模拟的假定。
1.3 数值模拟计算
按照定义的覆岩移动规律数值模拟边界条件进行一次求解,求解完成后,进入下一个单元的激活,如此反复,直至最后一个单元激活、加载,施加边界条件,求解完成,并输出结果,得到覆岩移动规律。通过模型求解将覆岩移动规律数值模拟结果分为以下4个阶段,分别为:老顶初次垮落阶段、次关键层垮落阶段、主关键层垮落阶段以及地表台阶式下沉阶段[6-7]。在以上 4个阶段中,周期来压步距是决定覆岩移动规律数值模拟精准程度的直接因素[8]。当覆岩荷载的不断增加,导致覆岩移动规律更加明显。综上所述,仿真结果能够高精度的表现出覆岩移动规律,也就是:当覆岩完全屈服后,覆岩移动规律以向上的态势迅速扩展,覆岩所受承载力会明显减小。
2 实测对比分析
2.1 实验准备
主要针对老顶初次垮落阶段得出的覆岩移动演化规律数值模拟结果进行实测对比分析,由模拟结果可以得知,当工作面扩大时,采空区内支承压力均值也会随之提升,最终达到覆岩的重量。设计井下现场对比实测,通过分析软件RFPA模拟得出初次来压步距与周期来压步距,实验对象同样选取10次工作面来压情况,并对预留煤柱的支承压力平均值、超前煤层的支承压力平均值以及采空区的支承压力平均值等参数进行具体设计。老顶来压期间采空区及两侧煤壁的支承压力平均值如表1所示。
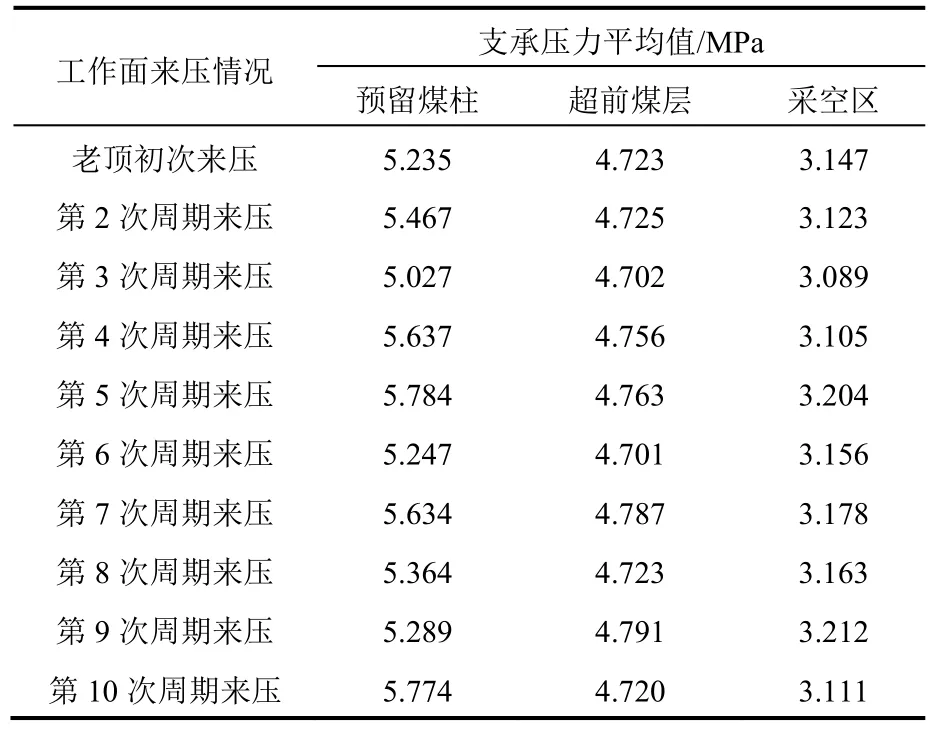
表1 老顶来压期间采空区支承压力平均值
根据表1所示,分别使用传统数值模拟方法以及本文设计数值模拟方法进行实验,设置传统的数值模拟方法为实验对照组。实验主要内容为:将10次周期来压覆岩移动规律的实测值与运用两种数值模拟方法得出的周期来压步距对比,从而评定数值模拟误差值更小,模拟性能更好的数值模拟方法。在此次的实验中,针对RFPA测得的数值模拟,记录实验结果,判断两种数值模拟方法对于矿区开采过程中覆岩移动规律的数值模拟能力。
2.2 实验结果分析与结论
根据上述设计的仿真实验步骤,采集 10组实验数据,将两种数值模拟方法的周期来压步距模拟误差值进行对比,对比结果如表2所示。

表2 周期来压步距模拟误差值对比
通过表2可得出:设计的数值模拟方法的周期来压步距模拟误差值最高为0.260 μm,实验对照组的为0.581 μm,设计的数值模拟方法可将周期来压步距模拟误差值降低一半左右,可以实现对覆岩移动规律的精准数值模拟。因此,本文设计数值模拟方法下得出的数值模拟结果与现场实测结果基本一致。通过实测对比结果证明,所设计的数值模拟方法其各项功能均满足设计总体要求,可以广泛应用于覆岩移动规律数值模拟方面。
3 结束语
通过实验证明,设计的数值模拟方法在覆岩移动规律数值模拟中的优势明显。本文通过建立覆岩移动规律数值模拟模型,总结了覆岩移动规律的模拟要点。数值模拟误差值的大小是保证覆岩移动规律数值模拟精准度的主要衡量标准,验证了支承压力平均值为覆岩移动规律数值模拟的主体内容。本文设计的数值模拟方法,能够完成传统数值模拟方法不能完成的任务。数值模拟方法旨在与实测数值基本一致,以此指导矿区开采过程中覆岩移动规律方面优化设计。当覆岩移动后,为了避免意外事件的发生,应先进行试采,并以此建立观测站进行定期观测,根据地表移动情况制定详细的矿区开采计划。但本文仅对覆岩移动规律数值模拟方法进行深入研究,没有对覆岩层长期稳定性方面进行深入分析,日后可以作为覆岩移动规律领域的重点研究方向。

