对高中《选修4-5》“绝对值不等式”一章的修改建议*——从练习册参考答案的一处错误说起
广东省肇庆市高要区第一中学(526100) 程华生
《选修4-5 不等式选讲》是人民教育出版社出版的,A 版,2007年1月第2 版,2016年12月第21 次印刷的.
我们采用的配套练习册,书名是:《金版学案高中同步辅导与检测》,该书是人民教育出版社和广东高等教育出版社联合出版,《高中同步辅导与检测》编写组编写,该书是经广东省中小学教辅材料评议委员会审核通过(2016年).
在使用练习册的过程中,发现了一处错误.
在练习册第13 页右上方有个第10 题.
题目为:求函数f(x)=|x-5|-|x+3|的最大值,并求出取最大值时x的范围.
与该练习册配套的参考答案如下:
解:f(x)=|x-5|-|x+3|≤|(x-5)-(x+3)|=8,当且仅当(x-5)(x+3) ≤0,即-3 ≤x≤5 时,等号成立.所以当-3 ≤x≤5 时,f(x)=|x-5|-|x+3|取得最大值为8.
参考答案有严重错误,误人子弟.
给出正确答案:
解:方法一:f(x)=|x-5|-|x+3|≤|(x-5)-(x+3)|=8,当且仅当(x-5)(x+3) ≥0 且|x-5|≥|x+3|时等号成立.⇒x≤-3,则f(x)的最大值为8,f(x)取最大值时,对应的x的取值范围为:x≤-3.
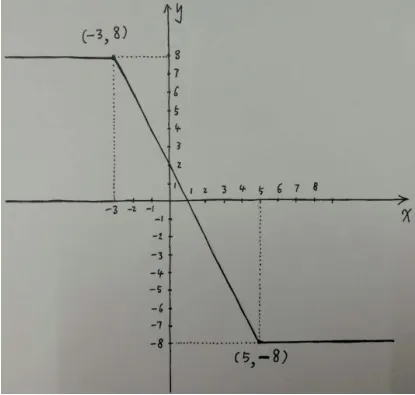
方法二:y=f(x) =|x -5| - |x+ 3|=f(x)的图象如下图:
明显可见,f(x)的最大值为8,f(x)取最大值时,对应的x的取值范围为:x≤-3.
我想,编者给出的参考答案之所以有错误,估计是对课本《选修4-5 不等式选讲》第14 页最上面的不等式|a|-|b|≤|a-b|≤|a|+|b|的“等号成立”的条件模糊不清导致的.
不等式|a| - |b|≤|a -b|≤|a|+|b|有重要价值和广泛应用,我建议将其修改完善后,取名为“推论1”.
建议“推论1”的表述如下:
推论1如果a,b是实数,那么|a|-|b|≤|a-b|≤|a|+|b|.左边的等号:当且仅当ab≥0 且|a|≥|b|时,等号成立.右边的等号:当且仅当ab≤0 时,等号成立.
并且,我还建议对课本第12 页的“定理1”进行修改完善,修改完善后,将会更好地为广大师生服务.
我建议修改完善后的“定理1”,表述如下:
定理1如果a,b是实数,那么|a|-|b|≤|a+b|≤|a|+|b|.左边的等号:当且仅当ab≤0 且|a|≥|b|时,等号成立.右边的等号:当且仅当ab≥0 时,等号成立.
如果对“定理1”进行修改完善,下面这些题目,就可以迎刃而解了.
练习题1:求函数y=f(x) =|x+4|-|3-x|的最大值,并求出f(x)取最大值时,对应的x的取值范围.
解:方法一:y=f(x) =|x+ 4| - |3-x|≤|(x+ 4) + (3- x)|= 7.当且仅当(x+4)(3- x) ≤ 0 且|x+ 4|≥|3- x|时 等 号 成立.⇒x≥3,则f(x) 的最大值为7,f(x) 取最大值时, 对应的x的取值范围为:x≥3.
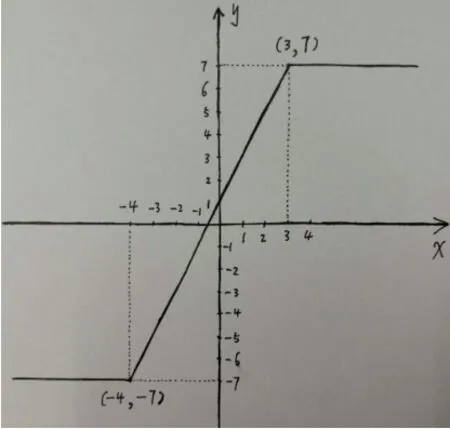
方法二:y=f(x) =|x+ 4| - |3- x|=的图象如下图:
明显可见,f(x)的最大值为7,f(x) 取最大值时, 对应的x的取值范围为:x≥3.
小结:方法一用到了“定理1”的左半部分:|a|-|b|≤|a+b|.当且仅当ab≤0 且|a|≥|b|时,等号成立.
练习题2:求函数y=f(x) =|x+2|+|4-x|的最小值,并求出f(x)取最小值时,对应的x的取值范围.
解:方法一:y=f(x) =|x+2|+|4-x|≥|(x+2)+(4-x)|= 6.当且仅当(x+2)(4-x) ≥0 时, 等号成立.(x+2)(4-x) ≥0 解得:-2 ≤x≤4.则f(x)的最小值为6,f(x)取最小值时,对应的x的取值范围为:-2 ≤x≤4.
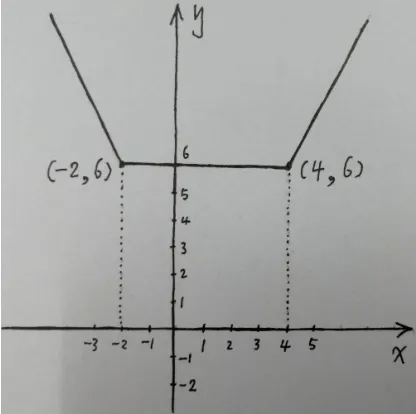
方法二:y=f(x) =|x+ 2|+|4- x|=的图象如下图:
明显可见:f(x)的最小值为6,f(x)取最小值时,对应的x的取值范围为:-2 ≤x≤4.
小结:方法一用到了“定理1”的右半部分:|a+b|≤|a|+|b|.当且仅当ab≥0 时,等号成立.
有了修改完善后的“推论1”,就可以避免练习册的编者也会犯下的严重错误,就可以非常顺利地解答如下题目:
练习题3:求函数y=f(x) =|x-4|-|x+2|的最大值,并求出f(x)取最大值时,对应的x的取值范围.
解:方法一:y=f(x) =|x -4| - |x+2|≤|(x -4)-(x+ 2)|= 6.当且仅当(x -4)(x+ 2) ≥ 0 且|x -4|≥|x+ 2|时, 等 号 成立.⇒x≤-2,则f(x)的最大值为6,f(x)取最大值时,对应的x的取值范围为:x≤-2.
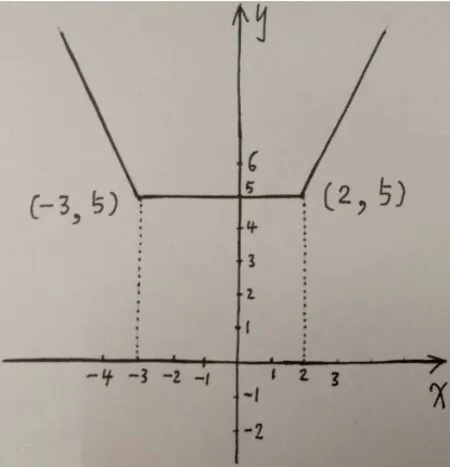
方法二:y=f(x) =|x -4| - |x+ 2|=的图象如下图:
明显可见:f(x)的最大值为6,f(x) 取最大值时, 对应的x的取值范围为:x≤-2.
小结:方法一用到了“推论1”的左半部分:|a|-|b|≤|a-b|.当且仅当ab≥0 且|a|≥|b|时,等号成立.

练习题4:求函数y=f(x) =|x+3|+|x-2|的最小值,并求出f(x)取最小值时,对应的x的取值范围.
解:方法一:y=f(x) =|x+3|+|x-2|≥|(x+3)-(x-2)|= 5.当且仅当(x+3)(x-2) ≤0 时, 等号成立.(x+3)(x-2) ≤0 解得:-3 ≤x≤2.则f(x)的最小值为5,f(x)取最小值时,对应的x的取值范围为:-3 ≤x≤2.
方法二:y=f(x) =|x+ 3|+|x -2|=的图象如下图:
明显可见:f(x)的最小值为5,f(x)取最小值时,对应的x的取值范围为:-3 ≤x≤2.
小结:方法一用到了“推论1”的右半部分:|a- b|≤|a|+|b|.当且仅当ab≤0 时,等号成立.
在“绝对值不等式”一章里面,修改完善后的“定理1”、“推论1”有极其重要的价值,有极其广泛的应用,使用频率极高,有必要将其熟记于心.
定理1如果a,b是实数,那么|a|-|b|≤|a+b|≤|a|+|b|.左边的等号:当且仅当ab≤0 且|a|≥|b|时,等号成立.右边的等号:当且仅当ab≥0 时,等号成立.
推论1如果a,b是实数,那么|a|-|b|≤|a-b|≤|a|+|b|.左边的等号:当且仅当ab≥0 且|a|≥|b|时,等号成立.右边的等号:当且仅当ab≤0 时,等号成立.
当“定理1”、“推论1”放在一起的时候,非常具有对称美,很容易记下来.

