指向共情的数学教学设计示例*——透过余弦定理的视点
安徽省淮北市烈山区淮北师范大学(235000) 王玉莹 郑云英
“人非草木,孰能无情”.教学过程中冷冰冰的知识和思想,学生难以主动接受,即使强制接受,也是暂时的,“只有饱含感情的知识,学生才乐于接受、理解、记忆和运用”[1].由此可见,要想在数学教学中获得满意的教学效果,帮助学生不只是“知其然”,更“知其所以然”,就必须传递饱含教师“感情”的数学知识.这种“感情”,其实就是师生共情的产物.蔡颖和戎幸[2]指出师生共情是开启学生心灵的一把钥匙,教师借助共情的课堂氛围可以帮助学生学习、理解新知识,同时也能够改善学生的学习态度,激发学习动机.共情为师生架起了一座沟通的桥梁,将共情真正融入到教师教学中去,是数学知识变成饱含“感情”的知识的关键.
1 “共情”的词源及心理学对“共情”内涵的界定
唐代诗人王贞白于《经故洛城》中言道:“几主任奸谄,诸侯各战争.但馀崩垒在,今古共伤情.”这里提到的“共伤情”其实就是共情,诗人望着眼前的残垣断壁,感伤之情油然而起.那么共情的来源究竟为何? 这种心理现象又是如何被界定的呢?
1.1 “共情”的词源
战国时期著名的思想家、教育家孟子于《孟子·公孙丑上》中曾提到:“今人乍见孺子将入于井, 皆有怵惕恻隐之心.”其中的“怵、惕、恻、隐”分别指“恐惧、惊骇、伤、痛”.这其实是人们对所见事物的一种移入式反应,儒家为研究这类复杂的人性问题,创立了一整套的社会哲学体系.在西方,美学最先对共情这一心理现象进行了系统的探讨:德国人赫尔曼·洛兹和罗伯特·费歇尔为了明确主体获得艺术作品含义的途径,创造了“Einfühlung”(“ein”代表进入;“fûhlung”代表感觉共鸣)一词来表达“人们把自己的情绪、情感映射到所见事物上”的能力.1909年,铁钦纳创造“empathy”一词来代表共情这一心理现象,标志着共情正式进入现代心理学的研究视野[3].国内多将“empathy”译为“共情”和“同理心”,其实本质上是一样的,但“同理心”多用于医学领域,而“共情”在心理学中使用较多[4].
1.2 心理学对“共情”内涵的界定
人本主义心理学家罗杰斯最早提出的心理学理论就是共情,其内涵包括三方面:其一,咨询师依据求助者的言语和行动去感受他内心的情感与思维;其二,咨询师基于自身的经验与知识,分析求助者的情感与思维与其本身的经历和人格之间的关系,以此发现问题的本质;其三,咨询师通过一定的方法与手段,把自己的共情传递给求助者,旨在对求助者产生影响并取得反馈[5].
从心理学的角度来说,共情是一种情绪、情感状态,是在观察、想象或推断他人情绪、情感状态的过程中产生的;共情与共情客体的情绪、情感状态形态一致,目标是自身以外的人.乐国安[3]表明共情包括如观点采择、自我和他人的区分、关于自我及他人情感状态的预存知识等一些对他人情绪、情感状态的认知评价成分.
共情作为一种间接性情绪,其发生机制与直接性情绪有所不同.主要区别在于外部刺激的作用对象:作用于自身而产生的情绪称为直接性情绪,而作用于他人产生的则是间接性情绪,也就是共情,它是设身处地体验他人情绪的一种方式.心理学家认为产生共情的心理机制包括条件反射、直接联想、模仿、象征性联想和充任角色五个方面.其中,充任角色与其他机制有所不同,它是指想象或设想他人所处情境的精确的认知能力[1].
这些年来,许多学者都深入研究了共情的涵义并给出定义.综合来看,共情是指个体经历(或想象)一个或多个个体的情绪情景时,首先产生与他人情绪情感的共享,而后在认知到自我与他人有区别的前提下,对其总体状况进行认知评估,从而产生的一种伴有相应行为(外显或内隐行为)的情绪情感反应,且主体将这种情绪情感和行为指向客体的心理过程[6].
2 “共情”在教学中的内涵
纵观心理学对共情的定义,基本都倾向于指向一个人的心理状态以及情感的感受.以往很多教师也针对共情理念提出了自己的想法及教学设计,但大多都只关注了教师与学生情感上的交流,即学生从教师的语言、行动等方面感受到被理解.其实共情不仅仅是指教师与学生情感上的共鸣与共振,也更应该包括师生知识上的承接与融合.
2.1 师生情感上的共鸣
教师与学生情感上的共鸣是指教师要打开学生的心门,进入学生的内心深处,体会他们的所思所行,体察他们的各种需求和情绪情感.
教师在日常生活中需要适时地运用言语对学生进行支持、鼓励和开导,设身处地的感受学生所感受的,体会学生所体会的,解决学生生活中和学习上遇到的困难和障碍.教师的语音语调、交谈距离都会影响师生共情的效果.一句温暖、鼓励的话语,学生就会如沐春风,走出阴霾,心情舒畅,增强自信,学习效果也会大大提高.教师对学生言语上的教导也要讲究方式方法,简单地说教、利用教师的权威去要求学生改正不当的行为,不仅会造成学生对教师产生抵触情绪,严重时更会导致学生对学习丧失兴趣和信心.这种情况下,教师可以采取自我暴露的方法,用自己过往的相似经历同学生产生共鸣,并通过这种方式传递给学生一定的道理,让学生自觉反省自己的行为.
除了言语上的交流,教师也应该注重非言语的传递.例如与学生交流时的面部表情、目光示意或是身体接触等,这些都会在无形之中拉近教师与学生心灵上的距离,更有助于师生共情的产生.
美国学者瑞安斯等人的研究发现:教师的共情和学生的学习成绩呈相关性.宋亚杰[1]表明善于共情的教师,学生更易对其所教学科产生兴趣,也会表现出更为多样且富有创造性的行为.师生建立情感上的共情,会帮助学生对教师产生信任感,易于向教师吐露心声,从而帮助教师快速找到问题的症结,以便对症下药.这种方式不仅能够帮助学生提高学习热情,建立学习自信,端正学习态度,还能体会“在正确的时间做正确的事情”的真正含义.
2.2 师生知识上的承接与融合
师生知识上的承接与融合是笔者所认为的“共情”更深层次的涵义,也是笔者认为“共情”更为重要的涵义.这其实是对知识的一种拟人化,即教师带着新知识走进课堂,期望通过贴近生活的课前准备和精心研究的教学设计,调动学生的学习兴趣,产生亟待解决的数学问题,并寻找学生已有的与问题相关联的知识单元,进而帮助教师将带来的新知识与学生原有知识结构中的知识单元发生承接与融合,产生知识上的“共情”,帮助学生实现新知识的登记和编码.
这种基于建立师生知识上的“共情”而进行的教学设计,更加符合学生的认知发展特点,教师能够设身处地的站在学生的角度去思考问题,找到新旧知识的关联点和新知识的难点,从而建立新知识的“合适根据地”,找到学生的最近发展区,鼓励学生主动学习、积极思考,能动地获取课堂知识,而不是“满堂灌”式的被动地接受新知识.
为了更加明了地表达共情的两种涵义,这里利用程序框图的形式对两种不同的共情进行展示(如图1):
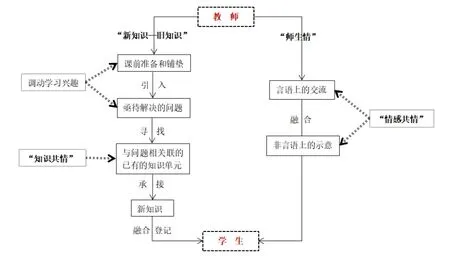
图1
3 指向共情的余弦定理教学设计
陆游诗云:“纸上得来终觉浅,绝知此事要躬行.”共情更深层次的内涵——师生知识上的承接与融合,必须通过课堂教学进行.在数学教学中应该如何设计才能真正帮助师生产生知识上的承接与融合呢? 这没有一个固定的教学模式可以规范性地执行.这里以“余弦定理”教学设计为例阐明课堂教学中师生如何承接知识、融合理念.
课例 余弦定理的教学设计
余弦定理 三角形中任何一边的平方等于其他两边的平方的和减去这两边与它们的夹角的余弦的积的两倍.即a2=b2+c2-2bccosA,b2=c2+a2-2cacosB,c2=a2+b2-2abcosC.
教师和学生要想产生知识上的融合与承接,首先要寻找与余弦定理相关的、亟待解决的数学问题,用数学问题激发学生的求知欲,引导学生不得不去思考问题的答案.
恰当的数学问题情境具有引入新课、推进一节课行进方向及其进程的作用[7].怎样的数学情境才能引起学生的共鸣呢? 在课堂教学中,反映学生真实生活的情境创设,更能帮助学生体验数学与现实的相关性,更利于学生主动发现问题、解决问题[8].由此可见,教师选择的问题既要与新知识相关,又要源于学生的现实生活,只有如此才能真正驱动学生主动探究问题的答案.笔者在余弦定理的教学设计中设计了如下问题,旨在从情感上和知识上引起学生的共鸣.
师:王刚骑车从家(A点)直线行驶了300 米到达了附近的超市(C点)购买学习用品,随后又直线行驶了400 米到达附近的公交站牌(B点),且CA与CB的夹角为60 度(如图2),若王刚从公交站牌继续直线骑行回家,那么王刚需要行驶多远的距离?

图2

图3
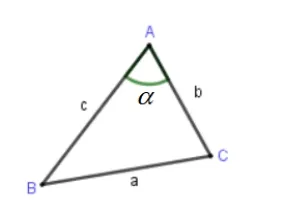
图4
【设计意图】这里选择了学生在生活中经常会遇到的一类问题,以现实生活中的实际问题为客观材料,激发学生解决问题的欲望,初步体会数学知识在实际生活中的应用,培养学生将实际生活中的问题进行数学化的能力,感受余弦定理的必要性与便捷性.
在引入了亟待解决的数学问题后,就需要教师寻找与该问题相关联的学生已有的知识单元去承接这个问题.学生在人教版数学(必修四)中已经掌握了与平面向量有关的知识,例如平面向量的表示方法、平面向量的线性运算以及平面向量的数量积等.学生头脑中与向量有关的知识其实就是与余弦定理相关的知识单元,现在就需要教师启发学生用自己掌握的向量知识去解决刚才提出的亟待解决的问题——王刚需要行驶多远的距离? 那么教师如何才能自然地启发学生调取与向量相关的知识来解决问题呢? 这里进行了如下的设计.
师:同学们,为了更加清晰的展示王刚直线行驶的路径,能否用带箭头的线段将其表示出来呢?
生:可以.如图3.
师:同学们看到图3 中带箭头的线段想到了什么?
生:向量! 带箭头的线段表示有向线段,向量可以用有向线段来表示.
【设计意图】教师引导学生利用带箭头的线段标注王刚的行驶路径,帮助学生自然而然地调动知识结构中与向量相关的知识去解决问题.这种处理方式促使学生不断地进行头脑风暴,并产生极高的参与感,最终在求知欲的驱使下,不断地主动寻找问题的答案.
接下来,就需要运用向量知识将先前的问题数学化,转变成纯数量问题继续探究,进而一步一个脚印地得到所要学习的新知识.
师:很好,如果将我们刚才的问题转化为纯数量问题,从平面向量的角度来看,题设中的已知条件可以如何转化?
生:可以转化为在三角形ABC中, 已知的夹角为(π-60°),求的值.
师:继续观察路径图,结合向量加法的三角形法则,你能得到怎样的等式?
生:可以将等式两边分别平方,就可以求出:
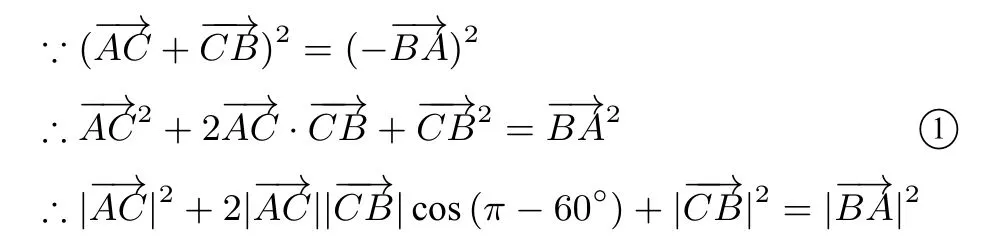
生:我们由①式可以得到:b2+2abcos(π-α)+a2=c2.化 简 得:b2-2abcosα+a2=c2.也 就 是:c2=a2+b2-2abcosα.
师:很好.从同学们得到的c2=a2+b2-2abcosα这个式子来看,当我们已知三角形的两条边的长度a和b,以及这两条边的夹角α(如图4),那么我们就可以直接求出第三条边的长度c.
师:这就是我们这节课要学习的余弦定理, 即三角形中任何一边的平方等于其他两边的平方的和减去这两边与它们的夹角的余弦的积的两倍.用数学语言表示为c2=a2+b2-2abcosC, 相应的, 我们也可以推导出b2=c2+a2-2cacosB、a2=b2+c2-2bccosA.由此可知,运用余弦定理我们仅需要一步运算就可以直接求出王刚家与公交站牌之间的距离.
【设计意图】教师引导学生调动出知识结构中与向量相关的知识点,将现实问题抽象为纯数量问题,完成数学化的过程,并试图用向量的知识加以解决.利用向量加法的三角形法则得到关系式并将此作为与新知识相关联的知识单元,经过一系列的化简及一般化,最终得到余弦定理.笔者将学生已经掌握的利用向量手段刻画三角形的三边关系作为“合适根据地”,运用与向量相关的知识同学生产生知识上的共鸣,帮助学生“跳一跳,摘桃子”,借助向量和向量的模之间的关系完成对三角形三边数量关系的探究.
这一系列的过程其实就是教师带来的新知识与学生已有的知识结构体系的承接与融合, 即完成了课堂教学中的“知识共情”,实现了学生对新知识——余弦定理的登记和承载.
4 结论
在实际教学过程中,如果教师不能找到学生原有认知结构中承接新知识的知识单元,就会出现“知识断层”,必定会产生学生无法跨越的“鸿沟”.师生的“知识共情”就是一座沟通新旧知识的“桥梁”, 帮助学生跨越知识的“鸿沟”.值得一提的是,这座“桥梁”是学生与教师共同搭建的,学生不仅具有极高的参与感,还能主动探究,最终到达成功的彼岸.“情感共情”促使教师和学生站在平等的位置,产生心与心的交流.教师在生活中和学习上的关怀不仅能帮助学生理解学习的真谛和意义, 还会带给学生坚定的力量和学习的自信.由此可见,不管是“情感共情”还是“知识共情”都是教师的一门必修课,只有把握好这两种不同的“共情”,才能在教学中游刃有余、挥洒自如,收获期望的教学效果.

