在专题复习中提升数学核心素养——以“二次函数综合性问题”为例

广东省广州市第二中学(510040) 温 晖 曾爱群

提升学生的数学核心素养,是初中数学专题复习的教学追求.笔者认为,初中数学专题复习要体现课型特征,注重学生参与,注重变式教学,着力提升学生的数学学科核心素养.

1 初中数学专题复习的教学特征

1.1 数学专题复习的基本特点

数学专题复习既要梳理所学知识、完善知识结构,又要揭示数学思想方法、提炼解题模式、完善认知结构、提升学生的数学核心素养.中考数学专题复习课具有两个基本特点：

(1)结构化.数学专题复习课要精选复习专题,通过典例分析和讲解,强化学生对数学双基的理解和掌握,将知识和方法结构化,完善学生的数学知识结构和认知结构.

(2)模式化.数学专题复习课要通过专题演练,优化数学思维方式,强化通性通法和一般解题策略,形成一类问题的解题模式,帮助学生形成知识迁移能力和解决问题能力,提升学生的数学核心素养.

1.2 数学专题复习的教学目标

数学专题复习的主要教学目标是使数学知识和方法结构化,提高知识迁移能力和问题解决能力,进一步提升学生的数学学科核心素养.

1.3 数学专题复习的教学模式

数学专题复习的常用教学模式有[1]：

先讲后练式：知识梳理——重点评析——问题变式——总结提炼——专题演练.

先练后讲式：解题尝试——典例示范——变式探究——回顾反思——专题演练.

2 初中数学专题复习的教学实录

案例：二次函数综合性问题.

本案例采用先练后讲式的专题复习模式,教学实录如下.

教学环节1：解题尝试.

上课伊始,教师提供人教版《义务教育教科书·数学》九年级上册第42 页第10 题第(3)题让学生独立求解,题目如下.

题目：根据二次函数图象上三个点的坐标：(-1,0),(3,0),(1,-5),求出函数的解析式.

(教学意图：复习待定系数法求二次函数的解析式,为解决二次函数综合性问题作铺垫.)

在学生用三种方法求出解析式y=后,引导学生总结二次函数有三种常见解析式.

一般式(定义式)：y=ax2+bx+c(a/=0);

顶 点 式(配 方 式) ：y=a(x - m)2+n(a /= 0), 其中(m,n) 为抛物线y=ax2+bx+c的顶点坐标, 且

两根式(零点式)：y=a(x-x1)(x-x2)(a/=0),其中x1,x2为方程ax2+bx+c=0 的两个根.

教学环节2：典例示范.

师：改变题目的已知条件,引入字母参数,与一次函数综合,可得如下考题.

例(2017年广州市初中毕业生学业考试第23 题)已知抛物线y1=-x2+mx+n,直线y2=kx+b,y1的对称轴与y2交于点A(-1,5),点A与y1的顶点B的距离是4.

(1)求y1的解析式;

(2)若y2随着x的增大而增大,且y1与y2都经过x轴上的同一点,求y2的解析式.

(教学意图：强化待定系数法求一次函数、二次函数的解析式,感悟函数与方程、分类讨论和数形结合等数学思想,提升数学运算和直观想象等核心素养.)

师：本题的已知条件是什么? 解题目标是什么? 用什么方法求解析式?

生1：第(1)问的已知条件是：y1的对称轴与y2交于点A(-1,5),点A与y1的顶点B的距离是4,解题目标是求二次函数解析式.可用待定系数法求二次函数的解析式.

生2：第(2)问的已知条件是：抛物线y1的对称轴与直线y2=kx+b交于点A(-1,5),点A与y1的顶点B的距离是4,y2随x的增大而增大,且y1与y2都经过x轴上的同一点.解题目标是求一次函数解析式.可用待定系数法求一次函数的解析式.

师：好！ 请独立求解,10 分钟后分享交流.

生3：(解法1)(1)因为y1=-x2+mx+n的对称轴与y2=kx+b交于点A(-1,5),所以=-1,所以m=-2,所以y1=-x2-2x+n.因为点A与y1的顶点B的距离是4,所以B(-1,1)或B(-1,9).把点B(-1,1)代入y1=-x2-2x+n,得-(-1)2-2×(-1)+n=1,n=0.把点B(-1,9)代入y1=-x2-2x+n,得-(-1)2-2×(-1)+n=9,n=8.所以y1=-x2-2x或y1=-x2-2x+8.

(2)因为y2=kx+b随着x的增大而增大,所以k ＞0.

①当y1=-x2-2x时,抛物线y1过x轴上的点(0,0) 和(-2,0).因为y2与y1的对称轴交于点A(-1,5),且y1与y2都经过x轴上的同一点,如图1.所以y2经过点A(-1,5),(-2,0).代入y2=kx+b,得解得所以y2=5x+10.

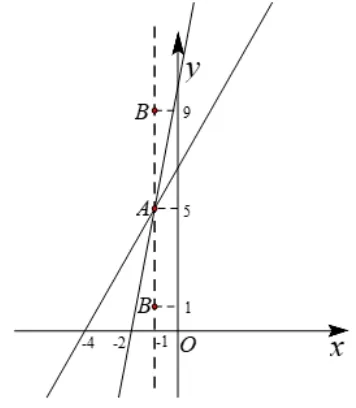
图1

②当y1=-x2-2x+8 时, 抛物线y1过x轴上的点(2,0)和(-4,0).因为y2与y1的对称轴交于点A(-1,5),且y1与y2都经过x轴上的同一点,如图1.所以y2经过点A(-1,5),(-4,0).代入y2=kx+b, 得解得所以

综上所述,y2=5x+10 或

生4：(解法2) (1) 同解法1得y1=-x2-2x+n,B(-1,1) 或B(-1,9).由抛物线顶点坐标公式, 得= 1 或= 9.所以n=0 或n=8,所以y1=-x2-2x或y1=-x2-2x+8.

(2) 因为y2与y1的对称轴交于点A(-1,5), 所以-k+b= 5,k=b -5, 所以y2= (b -5)x+b, 所以y2过x轴上的点因为y2=kx+b随着x的增大而增大,所以k ＞0,b ＞5.

①当y1=-x2-2x时, 抛物线y1过x轴上的点(0,0)和(-2,0).因为y1与y2都经过x轴上的同一点,所以=-2,解得b= 0(舍去),或b= 10.所以y2=5x+10.

②当y1=-x2-2x+8 时, 抛物线y1过x轴上的点(2,0) 和(-4,0).所以=-4, 解得(舍去),或b=所以y2=

综上所述,y2=5x+10 或y2=

生5：(解法3) (1) 同解法1 得y1=-x2-2x+n, 即y1=-(x+1)2+(1+n).因为点A与y1的顶点B的距离是4, 所以|1+n-5|= 4, 所以n= 0, 或n= 8, 所以y1=-x2-2x或y1=-x2-2x+8.

(2) 因为y2与y1的对称轴交于点A(-1,5), 所以-k+b= 5,b=k+5, 所以y2=kx+(k+5), 所以y2过x轴上的点因为y2=kx+b随着x的增大而增大,所以k ＞0.

①当y1=-x2-2x时, 抛物线y1过x轴上的点(0,0)和(-2,0).因为y1与y2都经过x轴上的同一点, 所以=-2, 解得k=-5(舍去), 或k=5.所以y2=5x+10.

②当y1=-x2-2x+8 时,抛物线y1过x轴上的点(2,0)和(-4,0).所以= 2,或=-4,解得k=(舍去),或k=所以y2=

综上所述,y2=5x+10 或y2=

师：很好！ 本题主要考查用待定系数法求一次函数、二次函数解析式、一次函数与二次函数的图象和性质、一元一次方程与一元二次方程的解法,考查推理能力、运算能力及分类讨论思想.

教学环节3：变式探究.

师：改变已知条件与解题目标,可得到变式1、2、3.

变式1：(2019年广州市初中毕业生学业考试第25 题节选)已知抛物线G∶y=mx2-2mx-3 有最低点.

(1)求二次函数y=mx2-2mx-3 的最小值(用含m的式子表示);

(2)将抛物线G向右平移m个单位得到抛物线G1.经过探究发现,随着m的变化,抛物线G1顶点的纵坐标y与横坐标x之间存在一个函数关系,求这个函数关系式,并写出自变量x的取值范围.

(教学意图：复习二次函数的最值与图象平移,提升学生的字母运算能力.)

师：本题的已知条件是什么? 解题目标是什么?

生6：第(1) 问的已知条件是抛物线G∶y=mx2-2mx -3 有最低点, 解题目标是求二次函数y=mx2-2mx-3 的最小值.

生7：第(2) 问的已知条件是抛物线G∶y=mx2-2mx-3 有最低点,将抛物线G向右平移m个单位得到抛物线G1,解题目标是求抛物线G1顶点的纵坐标y与横坐标x之间的函数关系式.

师：能独立给出本题的解法吗?

生8：(解法1)(1)因为抛物线G∶y=mx2-2mx-3有最低点, 所以m ＞0.因为y=mx2-2mx -3 =m(x2-2x)-3 =m(x-1)2-m-3,所以当x= 1 时,y取得最小值ymin=-m-3(m ＞0).

(2) 因为抛物线G∶y=mx2-2mx -3 有最低点,所以m ＞0.抛物线G向右平移m个单位得抛物线G1∶y=m(x-1-m)2-m-3,抛物线G1的顶点坐标为(m+1,-m-3).又因为抛物线G1的顶点坐标为A(x,y),所以两式相加消去m得：y=-x-2.(也可以代入消元：y=-m-3 =-(m+1)-2 =-x-2)所以y与x的的函数关系式为：y=-x-2.又因为m ＞0,所以x=m+1＞1,即x的取值范围为：x ＞1.

生9：(解法2) (1) 因为抛物线的对称轴为x== 1, 所以当x= 1 时,y取得最小值ymin=m·12-2m·1-3=-m-3(m ＞0).

(2)同解法1.

生10：(解法3)(1)因为抛物线G∶y=mx2-2mx-3 有最低点,所以m ＞0.由抛物线的顶点坐标公式,y的最小值为ymin==-m-3(m ＞0).

(2)同解法1.

师：很好！ 本题主要考查二次函数的最值、图象平移、一次函数的自变量的取值范围,考查字母运算能力及数形结合思想.

变式2：如图2,抛物线y=+ 3 与x轴交于A,B两点(点A在点B的左侧),与y轴交于点C.

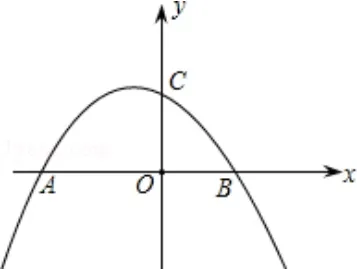
图2

(1)求点A,B的坐标;

(2) 设D为已知抛物线的对称轴上的任意一点, 当ΔACD的面积等于ΔACB的面积时,求点D的坐标;

(3)若直线l过点E(4,0),M为直线l上的动点,当有且只有一个点M满足AM ⊥BM时,求直线l的解析式.

在学生独立求解后,教师规范解题过程.

变式3：(2018年广州市初中毕业生学业考试第24 题)

已知抛物线y=x2+mx-2m-4(m ＞0).

(1)证明：该抛物线与x轴总有两个不同的交点;

(2)设该抛物线与轴的两个交点分别为A,B(点A在点B的右侧),与y轴交于点C,A,B,C三点都在⊙P上.

①试判断：不论m取任何正数,⊙P是否经过y轴上某个定点? 若是,求出该定点的坐标;若不是,说明理由;

②若点C关于直线x=的对称点为点E, 点D(0,1),连接BE,BD,DE,ΔBDE的周长记为l,⊙P的半径记为r,求的值.

(教学意图：建构二次函数综合性问题的认识结构,提升学生的学科核心素养.)

师：本题的已知条件是什么? 解题目标是什么?

生11：已知抛物线y=x2+mx-2m-4(m ＞0),第(1)问的解题目标是证明该抛物线与x轴总有两个不同的交点.

生12：第(2) 问的已知条件是该抛物线与x轴的两个交点分别为A,B(点A在点B的右侧) , 与y轴交于点C,A,B,C三点都在⊙P上,解题目标有两个：一是判断⊙P是否经过y轴上某个定点;二是求的值.

师：能独立给出本题的解法吗?

生13：(解法1) (1) 因为Δ =m2-4(-2m -4) =m2+8m+16=(m+4)2,因为m ＞0,所以(m+4)2＞0.所以该抛物线与x轴总有两个不同的交点.

(2) ①如图3,不论m取任何正数,⊙P经过y轴上定点(0,1).理由如下：令y=0,得x2+mx-2m-4=,因为Δ=(m+4)2, 所以x=所以x1== 2,x2=-m-2.因为m ＞0, 所以-m-2＜0,-m-2＜2.因为点A在点B的右侧, 所以B(-m-2,0),A(2,0).所以AO=2,BO=m+2.

图3

令x= 0, 得y=-2m-4,因为m ＞0,所以-2m-4＜0,C(0,-2m-4)在y轴的负半轴.所以OC=2m+4.因为A,B,C三点都在⊙P上, 所以⊙P也与y轴的正半轴有交点,设这个交点为K(0,k),即KO=k.

因为A,B,C,K四点都在⊙P上, 所以∠AKO=∠ABC.因为∠AOK= ∠COB= 90°, 所以ΔAOK∽ΔCOB, 所以所以k= 1.所以K(0,1).所以不论m取任何正数,⊙P经过y轴上定点(0,1).

②如图4,连接CE,由①知点D在⊙P上, 因为A,B都在⊙P上, 所以点P在直线x=上.因为点C关于直线的对称点为点E, 所以PC=PE,EC ⊥y轴于点C.所以∠DCE= 90°.所以DE是⊙P的直径,即DE=2r.

图4

在RtΔAOD中,AD=因为∠DBE= ∠DOA,∠BED= ∠OAD, 所以ΔBDE∽ΔODA.所以BD∶BE∶DE=DO∶OA∶AD= 1 ∶2 ∶设BD=x,则BE= 2x,DE=所以2r=即r=l=BD+BE+DE=x+2x+=(3+所以

生14：(解法2)(1)因为y=x2+mx-2m-4=(x-2)(x+m+2),令y= 0,得(x-2)(x+m+2) = 0, 所以x1= 2,x2=-m -2.因为m ＞0, 所以-m-2＜0.所以x1/=x2.所以该抛物线与x轴总有两个不同的交点.

(2) ①同解法1.

②如图5,因为A(2,0),B(-m-2,0),D(0,1),E(-m,-2m -4), 所以BD=

图5

所以BD2+BE2=DE2.所以ΔBDE是直角三角形, ∠DBE= 90°.所以DE= 2r=因为ΔBDE的周长为l,所以

所以

师：本题主要考查二次函数与坐标轴的交点、二次函数的对称轴、一元二次方程的根的判别式、一元二次方程、圆周角的性质、相似三角形的性质与判定、勾股定理等基础知识,考查学生的数学推理、数形结合能力.

教学环节4：回顾反思.

师：本节课复习了何种问题? 解决这种问题涉及哪些知识与方法?

生15：复习了二次函数综合性问题.

生16：二次函数综合性问题涉及一次函数与二次函数的解析式、图象和性质,一次函数与二次函数与坐标轴的交点,一元二次方程的根的判别式、一元二次方程的解法、圆的性质、相似三角形的性质与判定、勾股定理等基础知识.

师：求解二次函数综合性问题要灵活运用函数与方程思想、数形结合思想,要根据已知条件与解题目标,注重图形直观,寻找解决问题的不同方法,提高综合运用所学知识解决问题的能力.

教学环节5：变式演练.

临近下课,教师布置如下题目让学生课后演练.

已知抛物线y=mx2+(1-2m)x+1-3m与x轴相交于不同的两点A,B.

(1)求m的取值范围;

(2)证明：该抛物线一定经过非坐标轴上的一点P,并求出点P的坐标;

3 教学启示

3.1 专题复习要注重目标定向

“二次函数综合性问题”以二次函数的的图象与性质为基础,注重一次函数、一元二次方程、勾股定理、相似三角形、圆的性质等知识的综合融会,主要考查函数与方程、数形结合等基本数学思想.注重提升学生的数学运算、逻辑推理、直观想象等核心素养.从上述教学实录来看,教师注重综合运用相关核心知识解决问题,目标定位恰当,教学效果优良;学生明确复习目标,目标达成良好,积累了处理“二次函数综合性问题”的解题经验.

3.2 专题复习要注重问题引领

从上述教学实录来看,教师注重“问题引领”,以互动交流方式引导学生主动参与,形成了“二次函数综合性问题”的认知结构和解题模式.“问题引领”正是数学教学实现学生与教师“双中心”的一个十分有效的手段[2].本节课以课本习题演练入手,以中考真题的解法探讨与问题变式为重点,较好地彰显了学生的主体地位.

3.3 专题复习要注重变式探究

从上述教学实录来看, 教师注重方法变式和问题变式,通过方法变式引导学生数学思考,提升学生的推理、运算等数学核心素养; 通过问题变式引导学生认识问题结构特征,促进深度学习, 学生经历了综合运用知识解决问题的过程.这样的变式探究对培育学生的知识迁移能力、提升学科核心素养是富有成效的.

3.4 专题复习要注重回顾反思

实践表明, 自我效能感较高的学生积极参与数学活动,自主探究问题,自我评价意识较强,善于反思提炼.因此,为了增强学生的自我效能感,在专题复习中要引导学生回顾反思,积累数学活动经验,强化数学学习动机,体验学习成功的快乐.