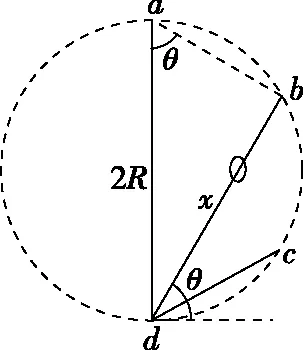
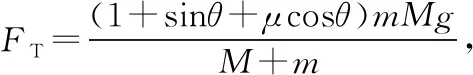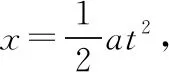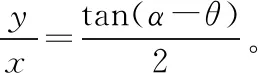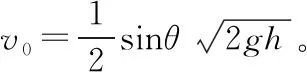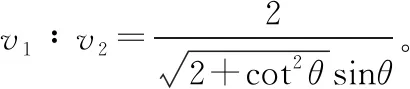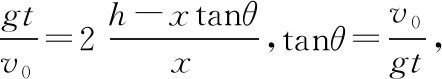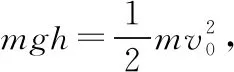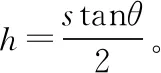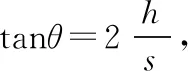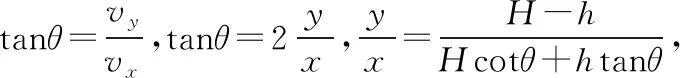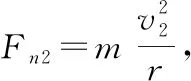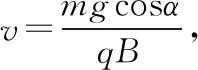再议斜面定理二十五例

重庆 李 昱 杨天才

高考物理试题从方位上看，不外乎水平、斜面、竖直，而斜面本身包含了其他两个方位，研究斜面上(内)物体的运动规律，对解决此类问题有事半功倍的效果，笔者总结了斜面定理五十七例，其中前三十二例已发表在《教学考试》(2018.1、2018.6)上，反响很好，下面将再列举二十五例。

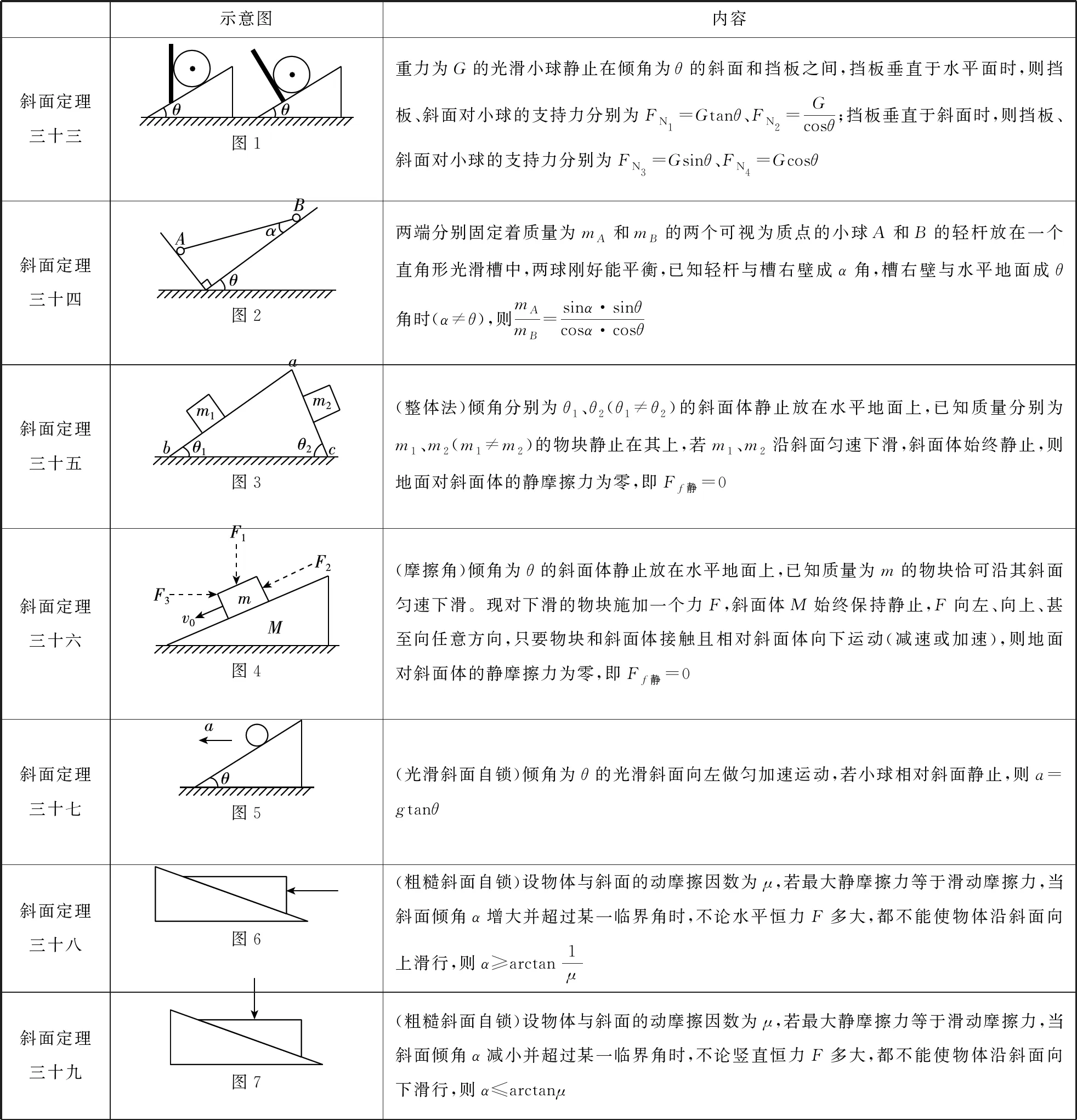
示意图内容斜面定理三十三图1重力为G的光滑小球静止在倾角为θ的斜面和挡板之间,挡板垂直于水平面时,则挡板、斜面对小球的支持力分别为FN1=Gtanθ、FN2=Gcosθ;挡板垂直于斜面时,则挡板、斜面对小球的支持力分别为FN3=Gsinθ、FN4=Gcosθ斜面定理三十四图2两端分别固定着质量为mA和mB的两个可视为质点的小球A和B的轻杆放在一个直角形光滑槽中,两球刚好能平衡,已知轻杆与槽右壁成α角,槽右壁与水平地面成θ角时(α≠θ),则mAmB=sinα·sinθcosα·cosθ斜面定理三十五图3(整体法)倾角分别为θ1、θ2(θ1≠θ2)的斜面体静止放在水平地面上,已知质量分别为m1、m2(m1≠m2)的物块静止在其上,若m1、m2沿斜面匀速下滑,斜面体始终静止,则地面对斜面体的静摩擦力为零,即Ff静=0斜面定理三十六图4(摩擦角)倾角为θ的斜面体静止放在水平地面上,已知质量为m的物块恰可沿其斜面匀速下滑。现对下滑的物块施加一个力F,斜面体M始终保持静止,F向左、向上、甚至向任意方向,只要物块和斜面体接触且相对斜面体向下运动(减速或加速),则地面对斜面体的静摩擦力为零,即Ff静=0斜面定理三十七图5(光滑斜面自锁)倾角为θ的光滑斜面向左做匀加速运动,若小球相对斜面静止,则a=gtanθ斜面定理三十八图6(粗糙斜面自锁)设物体与斜面的动摩擦因数为μ,若最大静摩擦力等于滑动摩擦力,当斜面倾角α增大并超过某一临界角时,不论水平恒力F多大,都不能使物体沿斜面向上滑行,则α≥arctan1μ斜面定理三十九图7(粗糙斜面自锁)设物体与斜面的动摩擦因数为μ,若最大静摩擦力等于滑动摩擦力,当斜面倾角α减小并超过某一临界角时,不论竖直恒力F多大,都不能使物体沿斜面向下滑行,则α≤arctanμ

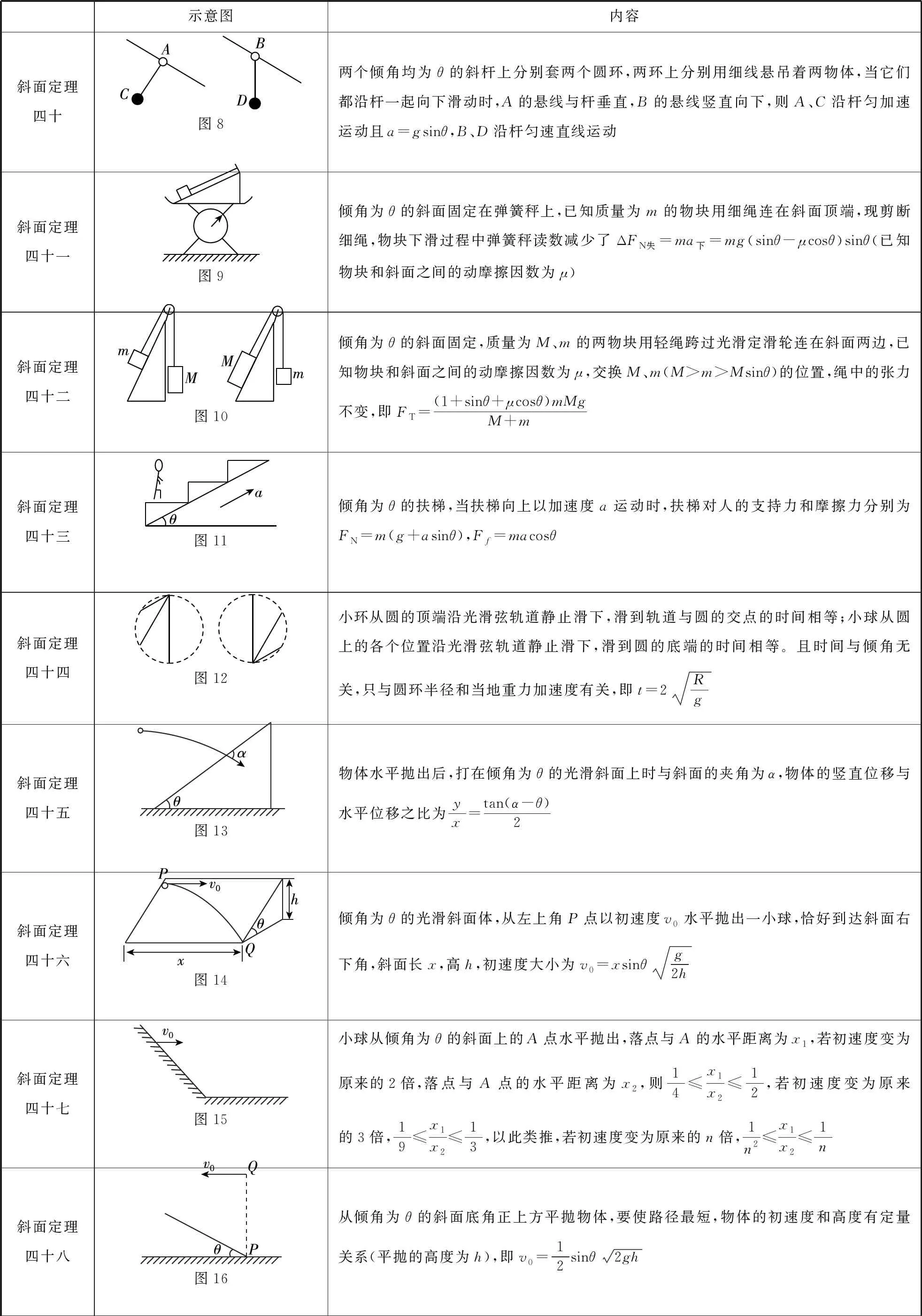
续表

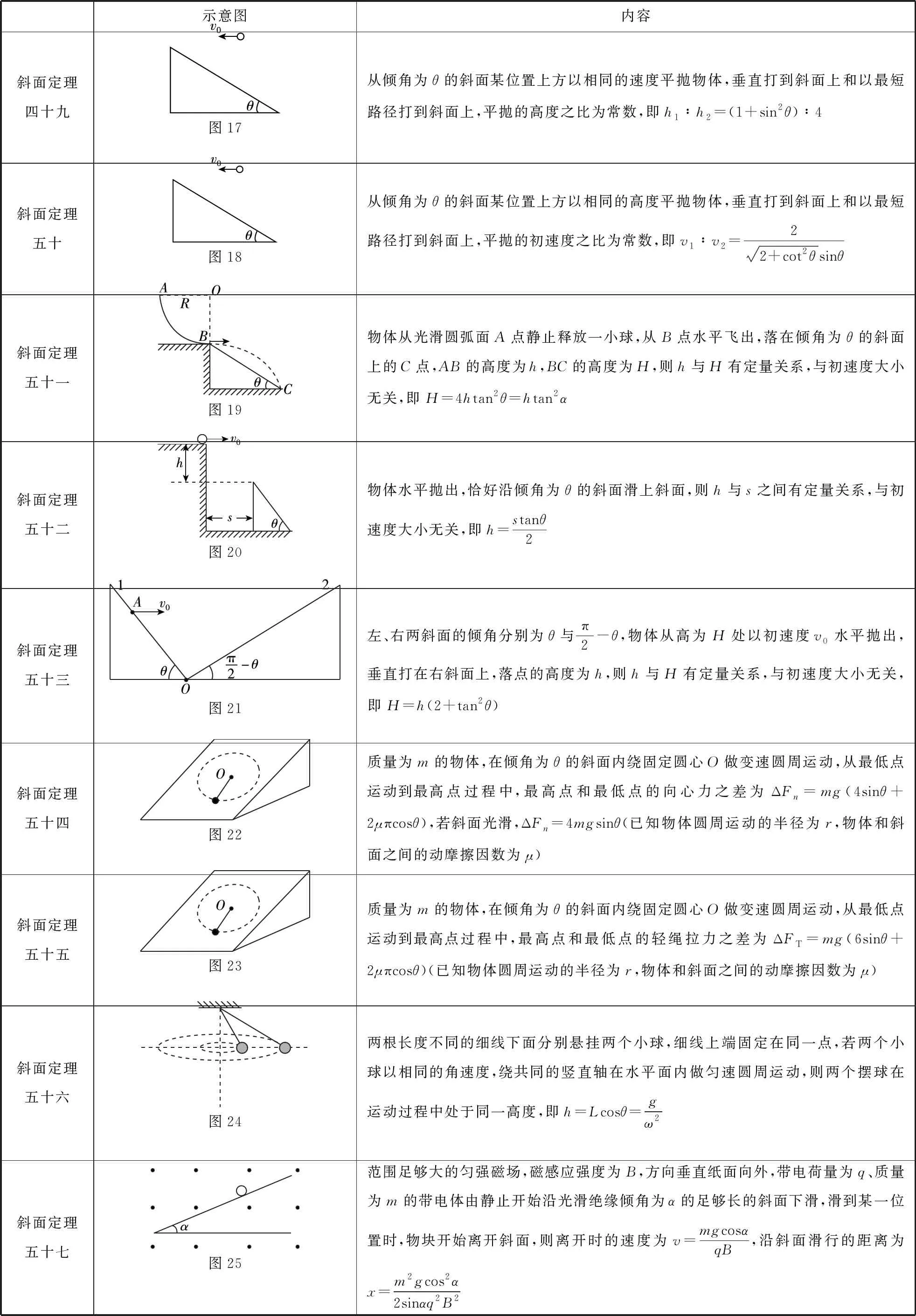
续表

以下是证明过程。

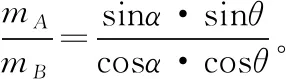
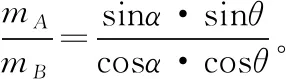
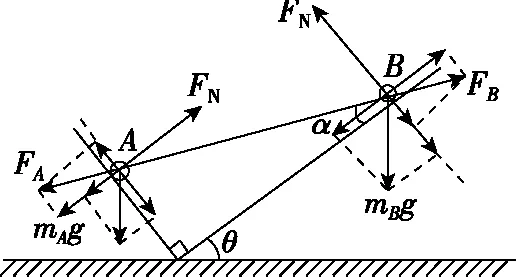
图26

【斜面定理三十五】如图3，倾角分别为θ1、θ2(θ1≠θ2)的斜面体静止放在水平地面上，已知质量分别为m1、m2(m1≠m2)的物块静止在其上，若m1、m2沿斜面匀速下滑，斜面体始终静止，则地面对斜面体的静摩擦力为零。

【解析】对任一物块进行受力分析，物块受重力、沿斜面向上的摩擦力、垂直斜面向上的支持力，由力的平衡条件可知，摩擦力和支持力的合力与重力等大反向，对斜面受力分析，受到重力、物块的作用力和地面的支持力，其中物块的作用力的方向竖直向下，斜面体不受水平方向的力，故地面与斜面体间无摩擦力，即Ff静=0。

【斜面定理三十六】如示意图4，倾角为θ的粗糙斜面体静止放在水平地面上，已知质量为m的物块恰可沿其斜面匀速下滑。现对下滑的物块施加一个力F，斜面体M始终保持静止，F向左、向上、甚至向任意方向，只要物块和斜面体接触且相对斜面体向下运动(减速或加速)，则地对斜面体的静摩擦力为零，即Ff静=0。

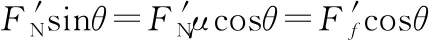
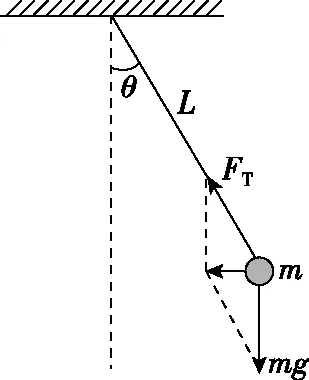
【斜面定理三十七】如示意图5，倾角为θ的光滑斜面向左做匀加速运动，若小球相对斜面静止，则a=gtanθ。

【解析】对小球进行受力分析和正交分解由牛顿第二定律有FNsinθ=ma，FNcosθ=mg，解得a=gtanθ。若斜面的加速度a>gtanθ，小球相对斜面沿斜面向上运动，若斜面的加速度a

【斜面定理三十九】如示意图7，设物体与斜面的动摩擦因数为μ，若最大静摩擦力等于滑动摩擦力，当斜面倾角α减小并超过某一临界角时，不论竖直恒力F多大，都不能使物体沿斜面向下滑行，则α≤arctanμ。

【斜面定理四十】如示意图8，两个倾角均为θ的斜杆上分别套两个圆环，两环上分别用细线悬吊着两物体，当它们都沿杆一起向下滑动时，A的悬线与杆垂直，B的悬线竖直向下，则A、C沿杆匀加速运动且a=gsinθ，B、D沿杆匀速直线运动。

【解析】如图27所示，设A环与杆间的摩擦力为Ff，对A环受力分析，由牛顿第二定律，有mAgsinθ-Ff=ma，对C物体受力分析，由牛顿第二定律，有mCgsinθ=ma，解得Ff=0，a=gsinθ；对D物体受力分析，由于做直线运动，合力与速度在一条直线上或者合力为零，故合力只能为零，物体做匀速运动，B、D一起沿杆匀速直线运动。

图27

若悬线的方向介于与杆垂直和竖直向下之间，两物体做匀加速运动，加速度满足0

【斜面定理四十一】如示意图9，倾角为θ的斜面固定在弹簧秤上，已知质量为m的物块用细绳连在斜面顶端，现剪断细绳，物块下滑过程中弹簧秤读数减少了ΔFN失=ma下=mg(sinθ-μcosθ)sinθ(已知物块和斜面之间的动摩擦因数为μ)

【解析】剪断绳后，对物块受力分析，由牛顿第二定律可知，物块沿斜面向下的加速度为a=g(sinθ-μcosθ)，将加速度分解为水平向左的ax=acosθ和竖直向下的ay=asinθ，其中ΔFN失=ma下=may=mg(sinθ-μcosθ)sinθ。若斜面光滑，ΔFN失=ma下=mgsin2θ。

【斜面定理四十三】如示意图11，倾角为θ的扶梯，当扶梯向上以加速度a运动时，则扶梯对人的支持力和摩擦力为FN=m(g+asinθ)，Ff=macosθ。

【解析】如图28所示，先将加速度分解为水平向右的ax=acosθ和竖直向上的ay=asinθ。对人受力分析，由牛顿第二定律，FN-mg=may，Ff=max，解得FN=m(g+asinθ)，Ff=macosθ。

图28

图29

【解析】从倾角为θ的斜面底角正上方以相同的速度平抛物体，垂直打到斜面上和以最短路径打到斜面上，由前面的结论可得，平抛的高度之比h1∶h2=(1+sin2θ)∶4。

【斜面定理五十一】如示意图19，物体从光滑圆弧面A点静止释放一小球，从B点水平飞出，落在倾角为θ的斜面上的C点，AB的高度为h，BC的高度为H，则h与H有定量关系，与初速度大小无关，即H=4htan2θ=htan2α。

11月9日，泰安市召开全市森林防火工作会议，签订新一轮森林防火期责任书，安排部署今冬明春的森林防火工作，动员全市上下立即行动，明确任务、压实责任，强化措施、严加防范，确保今冬明春的森林防火工作不出大问题。

【斜面定理五十四】如示意图22，质量为m的物体，在倾角为θ的斜面内绕固定圆心O做变速圆周运动，则最高点和最低点的向心力之差为ΔFn=mg(4sinθ+2μπcosθ)。(已知物体圆周运动的半径为r，物体和斜面之间的动摩擦因数为μ)

【斜面定理五十五】如示意图23，质量为m的物体，在倾角为θ的斜面内绕固定圆心O做变速圆周运动，则最高点和最低点的轻绳拉力之差为ΔFT=mg(6sinθ+2μπcosθ)。(已知物体圆周运动的半径为r，物体和斜面之间的动摩擦因数为μ)

图30

[注：本文系重庆市教育科学“十三五”规划2016年度青少年创新人才培养《普通高中培养青少年创新人才校本课程开发研究》专项课题阶段性成果(课题编号：2016-CX-14)]