用等温分态公式 解决变质量问题

广东 林东星

理想气体状态方程是历年高考选考题必考的知识点，以计算题的方式出现。理想气体状态方程，通常都是以一定质量的气体为研究对象。也就是说，对一定质量的气体变化的过程进行分析，学生容易理解。但是，生活中又常有涉及气体的变质量问题，学生不容易解决。例如2016年全国卷Ⅱ、2017年全国卷Ⅰ、2019年全国卷Ⅰ、2020年全国卷Ⅰ、2021年广东省普通高考适应性测试卷中的热学考题，都有涉及变质量问题。在解题中，学生如果能理解玻意耳定律等温分态公式，并运用等温分态公式解决问题，就能变得简洁高效。学生也可以从中体验到物理与生活息息相关，提高自身的核心素养。本文以试题为例，探讨如何利用等温分态公式，快速准确地解决理想气体的变质量问题。

玻意耳定律是英国科学家玻意耳和法国科学家马略特各自通过实验发现的，即一定质量的某种气体，在温度不变的情况下，压强P与体积V成反比，写成公式pV=C，或者p1V1=p2V2，其中C为常量，p1、V1、p2、V2分别是该气体在1、2两个状态的压强、体积状态参量。玻意耳定律只是理想气体状态方程一个方面的内容，而理想气体状态方程的另一种表达式为pV=nRT，其中：p为压强，V为气体体积，T为热力学温度，n为气体的物质的量，R为摩尔气体常数。因此，我们可以把一定质量的理想气体，根据问题情境的需要，在温度不变的情况下分成若干份不同状态的气体，推导出玻意耳定律等温分态公式，即pV=n1RT+n2RT+n3RT+…+nnRT=p1V1+p2V2+p3V3+…+pnVn。该公式常被用于处理气体的变质量问题，具体的问题情境一般分为三类：气体分装问题、充气问题和放气问题，本文在此分别加以分析与点评。

一、用等温分态公式解决气体分装问题

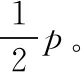
(ⅰ)两罐中气体的压强；

(ⅱ)甲罐中气体的质量与甲罐中原有气体的质量之比。

【解析】(ⅰ)常规解法：气体发生等温变化，对甲、乙两罐中的气体，可认为甲罐中原气体由体积V变成3V，乙罐中原气体体积由2V变成3V，则根据玻意耳定律分别有

pV=p1·3V

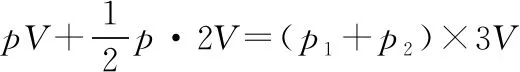
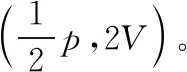
(ⅱ)常规解法：若调配后将甲罐中气体再等温压缩到气体原来的压强为p，则p′V=pV′

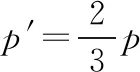
等温分态公式法：将甲罐中原有的气体看成一个整体，调配的过程相当于将甲中原有的气体分装后压强为p′，一部分气体留在甲罐中，另一部分气体调配到乙罐中，总体积变为V甲总。用等温分态公式求解，即pV=p′·V甲总

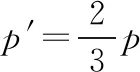
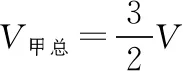
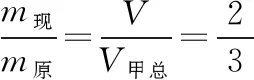
【点评】相比于常规解法，学生用等温分态公式法解题时，要会将变质量问题看成整体质量不变来处理。本题中，如果只看甲罐或者乙罐，那么单一罐中的气体在调配的过程中，就是一个变质量问题。但是，如果能把甲罐和乙罐看成一个整体，从这个角度来思考，气体整体的总质量却是不变的，温度也是保持不变的。只是分装在不同罐中的原有气体，有不同的压强和体积。这就是气体分装问题，可以使用等温分态公式求解。由此题可见，等温分态公式虽然需要通过玻意耳定律推导而来，但直接被运用到等温变质量的问题情境中，有一定的便利性，计算量少，不易出错。

二、用等温分态公式解决充气问题

【例2】(2021·广东省普通高考适应性测试卷)轮胎气压是行车安全的重要参数，某型号汽车轮胎容积V0为25 L，安全气压范围为2.4～3.0 atm。汽车行驶一段时间后，发现胎压下降到p1=2.0 atm，用车载气泵给其充气，气泵每秒钟注入0.5 L压强为p0=1.0 atm的空气。忽略轮胎容积与气体温度的变化。为使气压回到安全范围求气泵工作的时间范围。

【解析】常规解法：已知汽车轮胎容积V0=25 L，发现胎压下降到p1=2.0 atm，胎内空气相当于压强为p0=1.0 atm，体积为V1的空气。根据玻意耳定律有

p1V0=p0V1

当气泵给轮胎充气到安全气压最小值pmin=2.4 atm时，胎内空气相当于压强为p0=1.0 atm，体积设为Vmin的空气。根据玻意耳定律有pminV0=p0Vmin

由于气泵每秒钟注入ΔV=0.5 L，压强为p0=1.0 atm的空气，所以此充气过程需要时间为

代入数据得tmin=20 s

当气泵给轮胎充气到安全气压最大值pmax=3.0 atm时，胎内空气相当于压强为p0=1.0 atm，体积设为Vmax的空气。根据玻意耳定律有pmaxV0=p0Vmax

此充气过程需要时间为

代入数据得tmax=50 s

因此，气泵工作的时间范围为20 s≤t≤50 s

等温分态公式法：从轮胎外部向内部充气的过程，设已知条件每秒钟注入空气体积V=0.5 L，气泵工作t秒后轮胎内的压强为p。充气前后，由等温分态公式有

p1V0+t·p0V=pV0

代入数据得p=0.02t+2 (atm)

由于安全气压范围为2.4 atm≤p≤3.0 atm

代入解得气泵工作的时间范围为20 s≤t≤50 s

【点评】本题提供了给轮胎充气这种常见的生活现象，让学生思考如何应用物理知识解决生活中的问题。这体现了理论要运用到实践当中的思想，让学生形成科学的物理观念和思维，体验到物理与生活息息相关，从而提高自身的学科核心素养。对于充气过程，学生容易陷入轮胎内气体质量变大，不能对轮胎内空气直接运用理想气体状态方程求解的困境中。但是，如果学生能够将注入的空气与轮胎内原有的空气，看成一个整体，那么，变质量问题就可以转变为一定质量的问题，学生再运用玻意耳定律等温分态公式，就能快速准确地列方程求解。

【例3】(2019·全国卷Ⅰ)热等静压设备广泛用于材料加工中。该设备工作时，先在室温下把惰性气体用压缩机压入到一个预抽真空的炉腔中，然后炉腔升温，利用高温高气压环境对放入炉腔中的材料加工处理，改善其性能。一台热等静压设备的炉腔中某次放入固体材料后剩余的容积为0.13 m3，炉腔抽真空后，在室温下用压缩机将10瓶氩气压入到炉腔中。已知每瓶氩气的容积为3.2×10-2m3，使用前瓶中气体压强为1.5×107Pa，使用后瓶中剩余气体压强为2.0×106Pa；室温温度为27℃。氩气可视为理想气体。

(ⅰ)求压入氩气后炉腔中气体在室温下的压强；

(ⅱ)将压入氩气后的炉腔加热到1 227℃，求此时炉腔中气体的压强。

【解析】(ⅰ)常规解法：设初始时每瓶气体的体积为V0，压强为p0；使用后气瓶中剩余气体的压强为p1。假设体积为V0、压强为p0的气体压强变为p1时，其体积膨胀为V1。由玻意耳定律得

p0V0=p1V1

被压入到炉腔的气体在室温和p1条件下的体积为

V′=V1-V0

设10瓶气体压入完成后炉腔中气体的压强为p2，体积为V2。由玻意耳定律得

p2V2=10p1V′

联立并代入数据得

p2=3.2×107Pa

等温分态公式法：将10瓶气体看成一个整体，部分气体经过压缩机压入炉腔中，另外剩余部分留在10个气瓶中。由等温分态公式得

10p0V0=p2V2+10p1V0

代入数据得

p2=3.2×107Pa

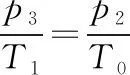
结合第一问并代入数据得

p3=1.6×108Pa

【点评】本题第(1)问中，压入氩气的过程实际上就是充气过程，充气前、后两个状态，温度都是室温。因此，可以运用玻意耳定律、等温分态公式。相比常规解法，学生运用等温分态公式法，只需要列一个算式，即可解得问题答案，方便快捷，且不易算错。特别是学生在考试过程中，能准确快速地解基础题，提高做题效率，剩余足够的时间，对于攻克难题，尤为重要。本题第(2)问是等容变化过程，体积保持不变，适用查理定律，显然不满足玻意耳定律、等温分态公式的适用条件。

三、用等温分态公式解决放气问题

【例4】(2016·全国卷Ⅱ)一氧气瓶的容积为0.08 m3，开始时瓶中氧气的压强为20个大气压。某实验室每天消耗1个大气压的氧气0.36 m3。当氧气瓶中的压强降低到2个大气压时，需重新充气。若氧气的温度保持不变，求这瓶氧气重新充气前可供该实验室使用多少天。

【解析】常规解法：设氧气在开始时的压强为20个大气压20p0，体积为V1，假设瓶中全部氧气在2个大气压2p0下的体积为V2。由于氧气的温度保持不变，根据玻意耳定律得

20p0V1=2p0V2

用去的氧气在2p0压强下的体积为

V3=V2-V1

设这些用去的氧气，在1个大气压p0下的体积为V0，根据玻意耳定律得

2p0V3=p0V0

每天消耗氧气体积，设为ΔV，则用去的氧气体积换算成可用的天数为

联立并代入数据得

N=4(天)

等温分态公式法：设氧气可用的天数为N天，1个大气压为p0。由于瓶中原有的全部氧气，最终变成为两部分，即剩余在瓶中的氧气和消耗掉的氧气。消耗过程中，氧气的温度保持不变，由等温分态公式有

20p0V1=2p0V1+p0N·ΔV

代入题给数据得N=4(天)

【点评】本题主要考查玻意耳定律的应用；学生使用常规解法解题，每一步都要明确研究的气体是什么，并且找到该气体在初末状态下的体积、压强等状态参量，然后列方程求解。如果使用等温分态公式解题，也要先明确研究的气体，只不过要将瓶中原有的氧气看成一个整体，最终变为两部分。其中消耗氧气可以看成放气过程，而且题目中强调氧气的温度保持不变，即暗示该过程满足玻意耳定律、等温分态公式。对比两种解法发现，等温分态公式简洁明了，是较为优化的解法。

【例5】(2017·全国卷Ⅰ)如图，容积均为V的气缸A、B下端有细管(容积可忽略)连通，阀门K2位于细管的中部，A、B的顶部各有一阀门K1、K3；B中有一可自由滑动的活塞(质量、体积均可忽略)。初始时，三个阀门均打开，活塞在B的底部；关闭K2、K3，通过K1给气缸充气，使A中的气体压强达到大气压p0的3倍后关闭K1。已知室温为27℃，气缸导热。

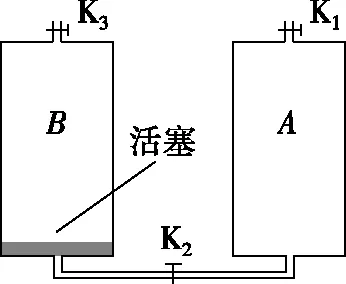
(ⅰ)打开K2，求稳定时活塞上方气体的体积和压强；

(ⅱ)接着打开K3，求稳定时活塞的位置；

(ⅲ)再缓慢加热气缸内的气体使其温度升高20℃，求此时活塞下方气体的压强。

【解析】(ⅰ)设打开K2后，稳定时活塞上方气体的压强为p1，体积为V1。依题意可知，两个气缸内的气体都经历等温变化过程。

常规解法：由玻意耳定律可知

对B中的气体有p0V=p1V1

对A中的气体有(3p0)V=p1(2V-V1)

等温分态公式解法：打开K2后，就是A中气体往B中充气的过程，由玻意耳定律等温分态公式，

对整体有：3p0V+p0V=p1·2V

对B中的气体有：p0V=p1V1

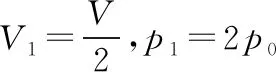
(ⅱ)打开K3后，由(ⅰ)问可知，活塞会上升。设在活塞下方气体与A中气体的体积之和为V2(V2≤2V)时，活塞下方气体压强为p2，由玻意耳定律得

(3p0)V=p2V2

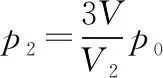
因此，打开K3后活塞上升直到B的顶部为止，此时

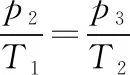
代入数据得p3=1.6p0

【点评】本题考查理想气体的状态方程，审题时要注意“气缸导热”这一条件，即第(ⅰ)小题所指的过程为等温变化过程。对于本题而言，两种解法列出来的方程，只有形式上的细微差别，优劣不分伯仲。所以说，对于封闭空间内的气体，经过等温变化后变成另外一个单一压强状态，用玻意耳定律常规表达式解题即可。在多种压强、体积状态的变质量问题中，使用等温分态公式的优势才比较明显。

四、结束语

从以上列举的五个例题中可以看到，等温分态公式在解决气体变质量问题时，具有方便快捷、简洁明了、不易算错等优势，特别是在分装气体、充气与放气问题上。等温分态公式实际上是玻意耳定律的内容，也是理想气体状态方程的内容。教师单独提出来讲解，让学生练习相关题型，并在生活现象中加以运用，解释生活现象，解决新问题。这样，有助于学生认识理想气体，形成物理观念，锻炼思维能力，提高物理核心素养。