“等效法”在高中物理解题中的应用

广东 陈庆贺

“等效法”又称为“等效替代法”，是指在保证某种效果(特性或关系)相同的情况下，将实际的、复杂的物理问题和过程转化为理想的、简单的物理问题的过程，从而巧妙地研究和处理问题的一种方法，这也是科学研究中常用的思维方法之一。等效法在高中物理教材中也多有涉及和渗透，如：力的合成和分解、运动的合成和分解、交变电流有效值的定义等。在高中物理解题过程中，如果能够合理地运用“等效法”，将有助于我们灵活、简洁地解决问题。本文将“等效法”在高中物理解题中的应用具体归纳如下：

一、等效力

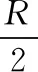
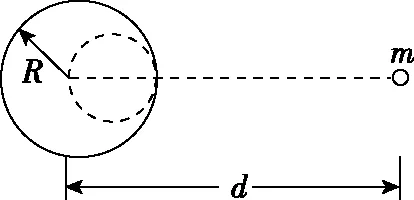
图1

【解析】由于该匀质球体被挖去了一个球形空穴，故我们不能将它看作是位于球心的、半径为R的质点而直接运用万有引力定律公式进行计算。但是，我们可以把整个匀质球体对小球的引力等效看成挖去的球体和剩余部分对小球的引力之和。其中完整的匀质球体对小球m的引力为

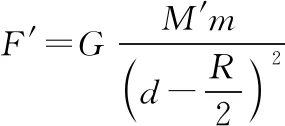
则该匀质球体剩余部分对小球的引力大小为

【点评】在此过程中，虽然不能直接运用万有引力公式进行计算，但是我们通过“等效法”，巧妙地把整个匀质球体对小球的引力看成挖去的球体和剩余部分对小球的引力之和，先分别应用万有引力公式计算出对小球m的万有引力大小，再进行相减，便可得到题目所要求的结果。这种等效替代的方法，也被称为“割补法”，在求引力问题时应用甚广。

二、等效场

在学习完电场之后，我们了解到各种各样的场也是一种特殊的物质，它们可相互叠加，两种或多种场能够同时占据同一空间从而形成一个叠加场。如带电体同时处于重力场和匀强电场之中，我们就可以把这两种场看作一个“等效重力场”，然后把问题转化为“等效重力场”的问题，可以利用重力场的知识和方法进行求解。

【例2】如图2所示，半径为r的绝缘光滑圆环固定在竖直平面内，环上套有一质量为m、带电荷量为+q的珠子，现在圆环平面内加一个匀强电场，使珠子由最高点A从静止开始释放(AC、BD为圆环的两条互相垂直的直径)，要使珠子沿圆弧经过B、C刚好能运动到D。求：

(1)所加电场的场强最小值及所对应的场强的方向；

(2)当所加电场的场强为最小值时，珠子由A到达D的过程中速度最大时对环的作用力大小；

(3)在(1)问电场中，要使珠子能做完整的圆周运动，在A点至少使它具有多大的初动能？

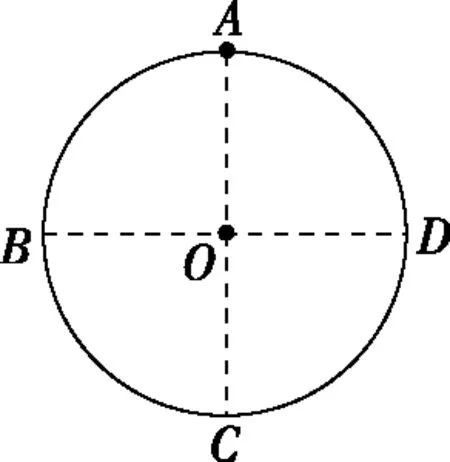
图2

且F电=qEmin

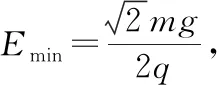
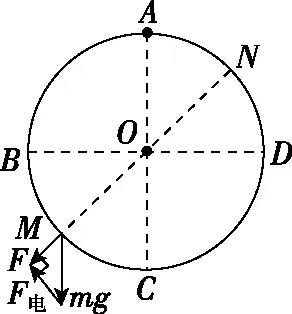
图3

(2)场强最小时电场力与重力的合力为

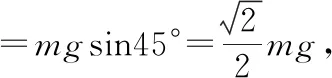
珠子由A运动到M的过程，由动能定理得

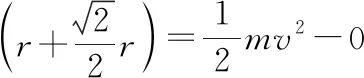
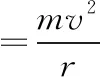
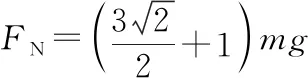
由牛顿第三定律可知，此时珠子对环的作用力大小为

(3)由题意可知，N点为等效最高点。

珠子由A到N的过程中，由动能定理得

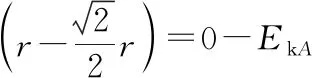
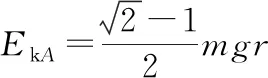
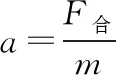
三、等效运动

运动的形式多种多样，很多情况下可以把物体的实际运动等效看作两个相互独立的分运动，然后分别对这两个分运动进行研究，再根据等时性把这两个分运动联系起来，如研究平抛运动、斜抛运动就是这种方法。因此，我们可以借助“等效运动”，实现“化曲为直”或“化折为直”，从而达到巧解题目之效。

【例3】回旋加速器的工作原理如图4所示，置于真空中的D形金属盒半径为R，两盒间狭缝的间距为d，磁感应强度为B的匀强磁场与盒面垂直，加在狭缝间的交变电压大小为U0。设一个质量为m、电荷量为+q的粒子在t=0时刻从A处飘入狭缝，其初速度可视为零，假设该粒子每次经过狭缝均做加速运动。求：

(1)粒子获得的最大动能Ek；

(2)粒子从飘入狭缝至动能达到Ek所需的总时间Δt。

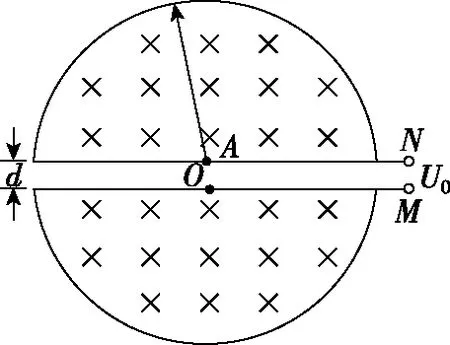
图4

【解析】(1)当粒子在磁场中的偏转半径达到R时动能最大

(2)粒子在磁场中偏转周期与速率无关，故其周期为

粒子在电场中每加速一次所获得的动能为qU0，设粒子被加速了n次，则有

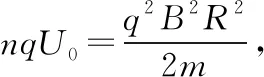
由于洛伦兹力不改变粒子的回旋速率，且粒子在电场中加速的加速度大小恒定，故可把粒子在电场中加速n次的折线运动等效看成初速度为0的匀加速直线运动，其位移为nd

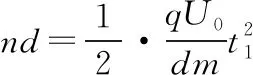
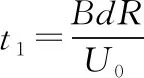
粒子在磁场中的运动的时间t2为

故粒子从飘入狭缝至动能达到Ek所需的总时间

【点评】在此题中，如果一段段地求解粒子在电场中加速n次所需的总时间，题目求解就会显得繁杂且计算量较大，但利用“等效法”巧妙地把粒子的运动看成初速度为0的匀加速直线运动，则大大地简化了求解过程，实现了“化折为直”的效果。本题中，求粒子在电场中的加速时间t1时，也可以利用动量定理求解，过程会更加简洁。

四、等效过程

物体在碰撞过程中常有机械能损失，除非发生的是弹性碰撞。但从能量守恒与转化的角度来看，无论是碰撞过程损失的机械能还是在运动过程受阻力作用而损失的机械能，并没有本质的区别。因此，在某些题设的条件下，可以把碰撞过程中损失的机械能等效看成由于阻力作用而损失的机械能，从而实现快速解题。

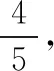
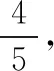
对小球运动全过程由动能定理，得mgh-fs=0

五、等效电源

根据直流电路知识可知，电源电动势E数值上等于电源未接入电路时的路端电压，电源内阻r等于外电路短路时电动势E与短路电流I的比值。根据此定义，可以把电路中的某些定值电阻与电路中原有的电源等效看作一个新的电源，从而使复杂的电路变得简单明了、方便计算，大大降低了直流电路的动态分析、求解可变电阻的电功率等问题的难度。其等效电源电动势和内阻的计算方法如下(证明过程从略)：

1.一个电动势为E、内阻为r的电源与阻值为R的电阻串联时，其等效电动势E′=E，等效内阻r′=r+R。

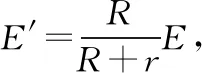
3.当电源和多个定值电阻构成混联电路后，其等效电动势等于被等效部分电路的路端电压，等效内阻等于原电源与其他定值电阻混联后的总电阻。

【例5】如图5所示的电路中，闭合开关S，当滑动变阻器的滑动触头P向下滑动时，四个理想电表的示数都发生变化，电表的示数分别用I、U1、U2和U3表示，电表示数变化量的大小分别用ΔI、ΔU1、ΔU2和ΔU3表示。下列说法正确的是

( )

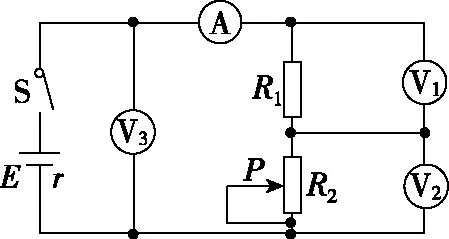
图5

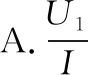
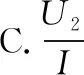
【答案】ACD

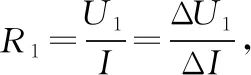
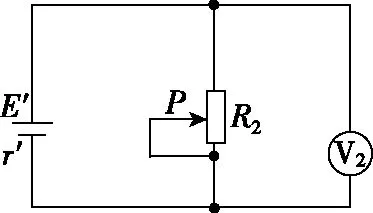
图6

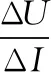
六、等效负载

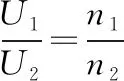
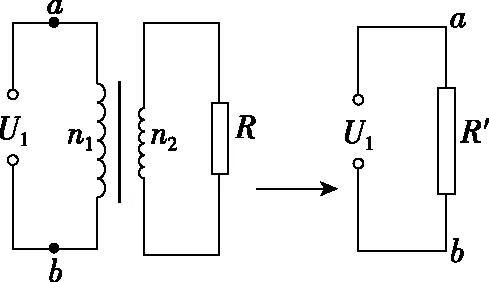
图7

【例6】一理想变压器的原、副线圈的匝数比为3∶1，在原、副线圈的回路中分别接有阻值相同的电阻，原线圈一侧接在电压为220 V的正弦交流电源上，如图8所示。设副线圈回路中电阻两端的电压为U，原、副线圈回路中电阻消耗的功率的比值为k，则

( )

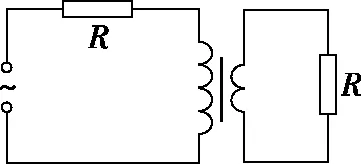
图8

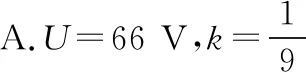
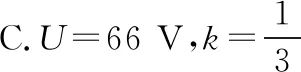
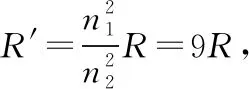
图9

【点评】这道题目如果运用常规解法，就要根据理想变压器的规律，将原线圈中的电压、电流都用副线圈的电压、电流来表示，然后再通过列方程组来求解。这种做法公式较多、计算复杂，容易出现错误。但是使用“等效负载”的方法解题，过程则简单得多。

目前，新高考评价体系下的高考命题，更加强调考查综合性和创新性，更加明显地渗透着对物理思想和物理方法的考查。等效思想和方法作为一种迅速解决物理问题的有效手段，将更加直接地体现于高考的命题之中。因此，有意识地体会物理等效思想的内涵和本质，掌握等效方法及其在解题中的应用，将会为我们的高考备考提供更强大的助力。