高阶Bernstein-Markov型不等式

金曼莎，章仁江，王子睿

(浙江工商大学统计与数学学院，浙江 杭州 310018)

0 引 言

Bernstein不等式是多项式或三角多项式导数的一种估计式，Markov不等式是一种多项式的导数不等式，这2个不等式在函数逼近论、计算数学中有重要的应用，尤其加权Bernstein-Markov不等式在多项式的带权逼近等研究方面起着重要的作用。Bernstein-Markov不等式中的最佳常数仍然是一个未解决的问题，是许多国内外学者关注的对象[1]。近年来，各种范数下的Bernstein-Markov不等式有所发展，文献[2]用矩阵的最大特征值的平方根刻画了几种不同权函数的Bernstein-Markov不等式的最佳常数，但文献[3]指出文献[2]中的最佳常数是错误的。文献[4]计算出权为e-x的Bernstein-Markov不等式的渐近精确常数。文献[5]给出了各类推广形式的Bernstein算子的加权Bernstein-Markov型不等式及正逆定理。文献[6]证明了在许多情况下，指数型Bernstein-Markov不等式中的常数是n次代数多项式在n→∞时相应不等式中常数的极限。文献[7]研究了序列和多项式的离散加权Markov-Bernstein不等式，并给出了相应的最佳常数。本文主要研究勒让德正交多项式所对应的二阶导Bernstein-Markov型不等式，给出一个使不等式成立的较小常数，并证明这个最佳常数的阶数为8。

1 定理及证明

定理设f(x)为1个次数不超过n次的多项式，则

其中常数的阶数8是不可改进的。

证明设Pn(x)为n次Legendre多项式，由Legendre多项式的积分性质[8]可得：

(1)

由Legendre多项式的导数递推公式可求得：

P′n(x)=(2n-1)Pn-1(x)+P′n-2(x)=

(2n-1)Pn-1(x)+(2n-5)Pn-3(x)+P′n-4(x)=

…=

(2)

f(x)为1个次数不超过n次的多项式，则f(x)可以用Pn(x)的线性组合来表示，即存在唯一的实数ai(i=0,1,…,n)使得：

f(x)=anPn(x)+an-1Pn-1(x)+…+a1P1(x)+a0P0(x)

则

(3)

当n为奇数时，对f(x)求一阶导，得到：

f′(x)=anP′n(x)+an-1P′n-1(x)+…+a1P′1(x)=

(2n-1)anPn-1+(2n-3)an-1Pn-2+(2n-5)(an+an-2)Pn-3+…+

3(an-1+…+a2)P1+(an+…+a1)P0

对f′(x)继续求导，得到：

f″(x)=(2n-3)(2n-1)anPn-2+(2n-5)(2n-3)an-1Pn-3+

(2n-7){[(2n-1)+(2n-5)]an+(2n-5)an-2}Pn-4+

…+

[2(n-2k)+1]〈{(2n-1)+…+[2(n-2k+1)+1]}an+

{(2n-5)+…+[2(n-2k+1)+1]}an-2+…+[2(n-2k+1)+1]an-2k+2〉Pn-2k+

[2(n-2k-1)+1]〈{(2n-3)+…+[2(n-2k)+1]}an-1+

{(2n-7)+…+[2(n-2k)+1]}an-3+…+[2(n-2k)+1]an-2k+1〉Pn-(2k+1)+

…+

3{[(2n-1)+(2n-5)+…+5]an+[(2n-5)+…+5]an-2+…+5a3}P1+

{[(2n-3)+(2n-7)+…+3]an-1+[(2n-7)+…+3]an-3+…+3a2}P0

(4)

由式(1)和式(4)可得：

…+

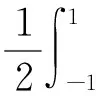
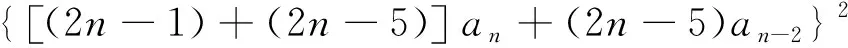
[2(n-2k)+1]〈{(2n-1)+…+[2(n-2k+1)+1]}an+

{(2n-5)+…+[2(n-2k+1)+1]}an-2+…+[2(n-2k+1)+1]an-2k+2〉2+

[2(n-2k-1)+1]〈{(2n-3)+…+[2(n-2k)+1]}an-1+

{(2n-7)+…+[2(n-2k)+1]}an-3+…+[2(n-2k)+1]an-2k+1〉2+

…+

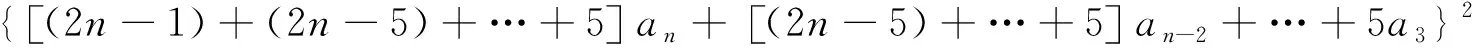
(5)

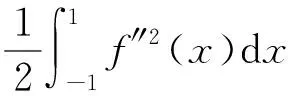
(6)

令

其中

要使得任意的a,I恒大于或等于0，只要矩阵B正定。由矩阵对角占优正定，考察矩阵B的任意一行n1。

(a)当n1为奇数时，令

(7)

(b)当n1为偶数时，令

(8)

只要取a的值使得式(7)与式(8)成立，则矩阵正定，当n1为奇数时3≤n1≤n，由式(7)得：

a≥(2n1+1)(an1,3+an1,5+an1,7+…+an1,n)

(9)

令

S(n1)=(2n1+1)(an1,3+an1,5+an1,7+…+an1,n)， 3≤n1≤n

求常数a的取值范围只需求S(n1)的最大值，即

a≥Smax(n1)

由式(5)、式(6)可求得：

则有：

an1,3+an1,5+an1,7+…+an1,n=3[(2n1-1)+(2n1-5)+…+5]{5+(5+9)+

(5+9+13)+…+[5+…+(2n-1)]}+7[(2n1-1)+(2n1-5)+…+9]

{9+(9+13)+(9+13)+17)+…+[9+…+(2n-1)]}+

…+

(2n1-3)(2n1-1){(2n1-1)+[(2n1-1)+(2n1+3)]+…+[(2n1-1)+…+(2n-1)]}

(10)

式(10)等号右边为3个数列的乘积，分别设这几个数列为Am,Bm,Cm。

现分别求Am,Bm,Cm的通项，数列Am为3，7，11，…，2n1-3，易求Am的通项为：

Am=4m-1

数列Bm为：

(2n1-1)+(2n1-5)+…+5,(2n1-1)+(2n1-5)+…+9,…,(2n1-1)+(2n1-5),2n1-1

数列Bm中第m项为：

数列Cm为：

5+(5+9)+…+[5+…+(2n-1)],9+(9+13)+…+[9+…+(2n-1)],
…,(2n1-1)+[(2n1-1)+(2n1+3)]…+[(2n1-1)+…+(2n-1)]

其中第m项为：

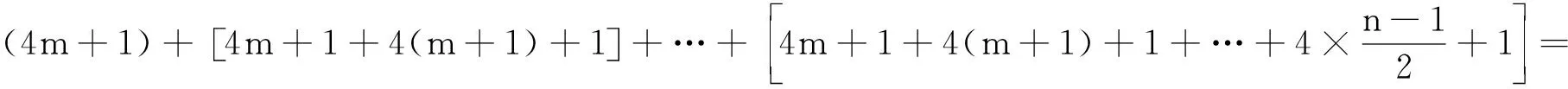
则有：

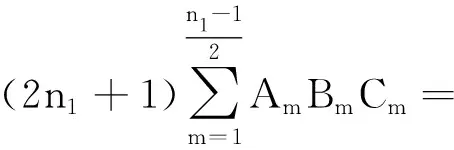
(11)

同理，当n1为偶数时2≤n1≤n-1，有：

(12)

对比式(11)与式(12)，取

当n为偶数时，同理可得：

(13)

由式(5)得：

…+

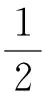
[2(n-2k)+1]〈{(2n-1)+…+[2(n-2k+1)+1]}an+

{(2n-5)+…+[2(n-2k+1)+1]}an-2+…+[2(n-2k+1)+1]an-2k+2〉2+

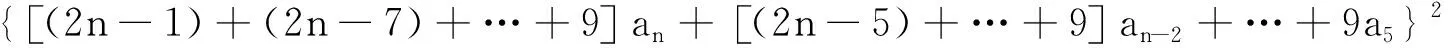
(14)

式(14)中不等号右边任意第k项为：

[2(n-2k)+1][2(n-2k+2)+1]〈{(2n-1)+…+[2(n-2k+1)+1]}+

{(2n-5)+…+[2(n-2k+1)+1]}+…+[2(n-2k+1)+1]〉2=

则由式(14)可得：

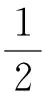
(15)

由式(13)、式(15)可得：

证毕。

2 结束语

本文结合正交多项式的导数递推性质与带权积分性质，利用矩阵对角占优正定的性质，求解出权为1时的二阶Bernstein-Markov型不等式的一个较小的常数。不同权函数、同种权函数不同阶导数所对应的Bernstein-Markov型不等式的最佳常数不一样，因此这类不等式还有很多方面值得深入探讨。