基于特征谱分析的领导-追随者网络一致性

李一帆，孙伟刚

(杭州电子科技大学理学院，浙江 杭州 310018)

0 引 言

多智能体系统一致性理论在人工智能、通信与控制等领域有着广泛的应用，如无人机编队、卫星协同工作。多智能体一致性指通过设计各个智能体之间的一致性协议，利用智能体之间的局部信息，不断调整自己的行为，使得所有智能体的状态最终达到一致[1-2]。作为一类重要的一致性问题，领导-追随者多智能体系统的一致性越来越受关注，其中领导者的状态不受其它智能体影响，而其它智能体尽可能追随领导者[3]。由于多智能体系统无法避免噪声的干扰，因此研究系统对噪声的鲁棒性非常重要。2010年，Patterson等[4]提出了含有噪声的领导-追随者网络一致性概念，在H2范数下，证明了领导-追随者网络一致性是由拉普拉斯矩阵的特征谱所决定，同时提出几种用于选择领导者的贪婪算法，从而使得网络达到最优一致性。Yi等[5]研究了一个领导者的无标度小世界Koch网络，得到领导-追随者一致性的精确结果，并指出网络的一致性不仅与领导者到中心节点的最短路径有关，还取决于领导者的度。众所周知，网络的拓扑结构决定了其特征谱，因此计算网络的特征谱面临着技术挑战。目前，给出含有多个领导者的领导-追随者网络一致性精确解的相关研究文献鲜少，同时，领导者数目对一致性是否有影响也值得深入探讨。为此，本文借助一类确定性网络模型[6]，得到含有多个领导设置的一致性解析表达式，揭示领导者对一致性影响的机理。

1 预备知识

1.1 拉普拉斯矩阵

记G是一个由N个节点组成的无向连通网络。设A=[Aij]N×N是G的邻接矩阵，如果节点i和节点j之间有连接，则Aij=Aji=1(i≠j)，否则，Aij=Aji=0。令D=diag{k1,k2,…,kN}为G的度对角阵，其中ki为节点i的度，则网络的拉普拉斯矩阵为L=D-A。

1.2 领导-追随者网络一致性

N维系统的领导-追随者网络的动力学表示如下：

(1)

式中，x(t)是状态向量，I是单位矩阵，H=diag{h1,h2,…,hN}，如果节点i是领导者，则hi=1，否则hi=0，η(t)表示高斯白噪声。

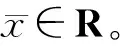
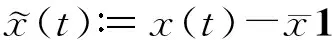
(2)

式中，1表示元素全为1的向量。

将式(2)代入式(1)，可得：

假设系统有α个节点为领导者，剩余N-α个节点为追随者。追随者受到噪声干扰并根据局部信息调整自己的状态。令xl(t)和xf(t)分别表示领导者和追随者的状态，则系统(1)可以写为：

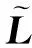
定义领导-追随者网络一致性定义为偏离领导节点状态的平均稳态方差[5]，即：

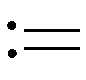
文献[5]的研究成果表明，领导-追随者网络的一致性可以由拉普拉斯主子阵的特征值来表示，即：

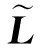
2 一类特殊网络拉普拉斯主子阵的特征谱计算

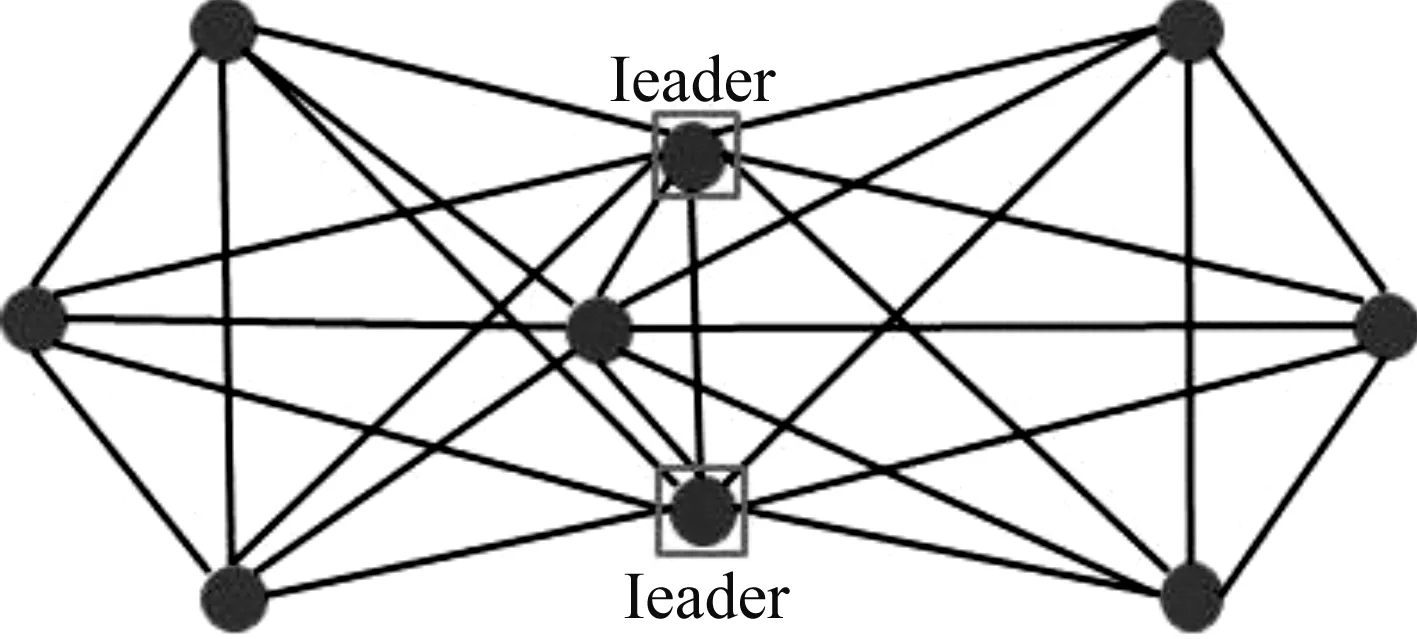
图1 具有2个领导者的网络模型

由于网络拓扑结构多样性，解析计算领导-追随者网络一致性结果面临技术挑战。本文选取由3个参数控制的一类windmill-网络模型作为研究对象[7]，网络模型由l个中心节点和m个kn-完全图组成的社团连接而成，其中kn的每个节点都与l个中心节点连接，并且l个中心节点组成一个kl-完全图。根据网络拓扑结构特点，网络节点总数N=mn+l。具有2个领导者的网络模型W(3,2,3)结构如图1所示。

根据网络W(l,m,n)的拓扑结构，其拉普拉斯矩阵L为：

式中，J是元素全为1的矩阵，0是零矩阵。本文在中心节点中随机选取α个节点作为领导者，即在该网络的拉普拉斯矩阵中删除领导者所在的行和列，则该网络的拉普拉斯主子阵表示为：

从第2列开始，将每1列加到第1列，可得：

(3)

根据行列式的特征，继续将每1列加到第1列，再将第1行乘以-1加到每1行，可得：

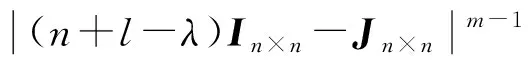
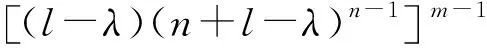
(α-λ)(mn+l-λ)l-α-1(mn+1-λ)(l-λ)m-1(n+l-λ)m(n-1)

(4)

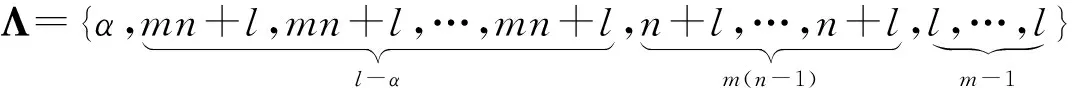
3 领导-追随者网络一致性分析

根据定义，网络的一致性的精确表达式如下：

(5)

当参数n→∞，HLF→0时，网络随着n的增大最终趋于一致。选取参数l=25，m=10，进行数值模拟，当领导者数目分别为2，4，8时，参数n对网络一致性的影响如图3所示。从图3可以看出，n越大，网络一致性越好，与理论解析结果相符。

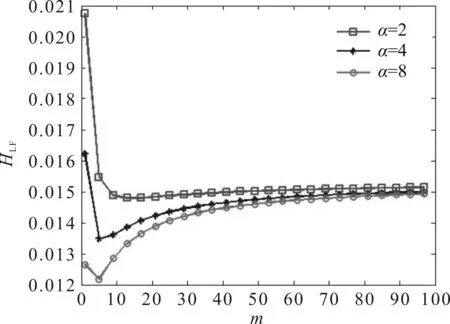
图2 不同领导者数目下，参数m对网络一致性的影响

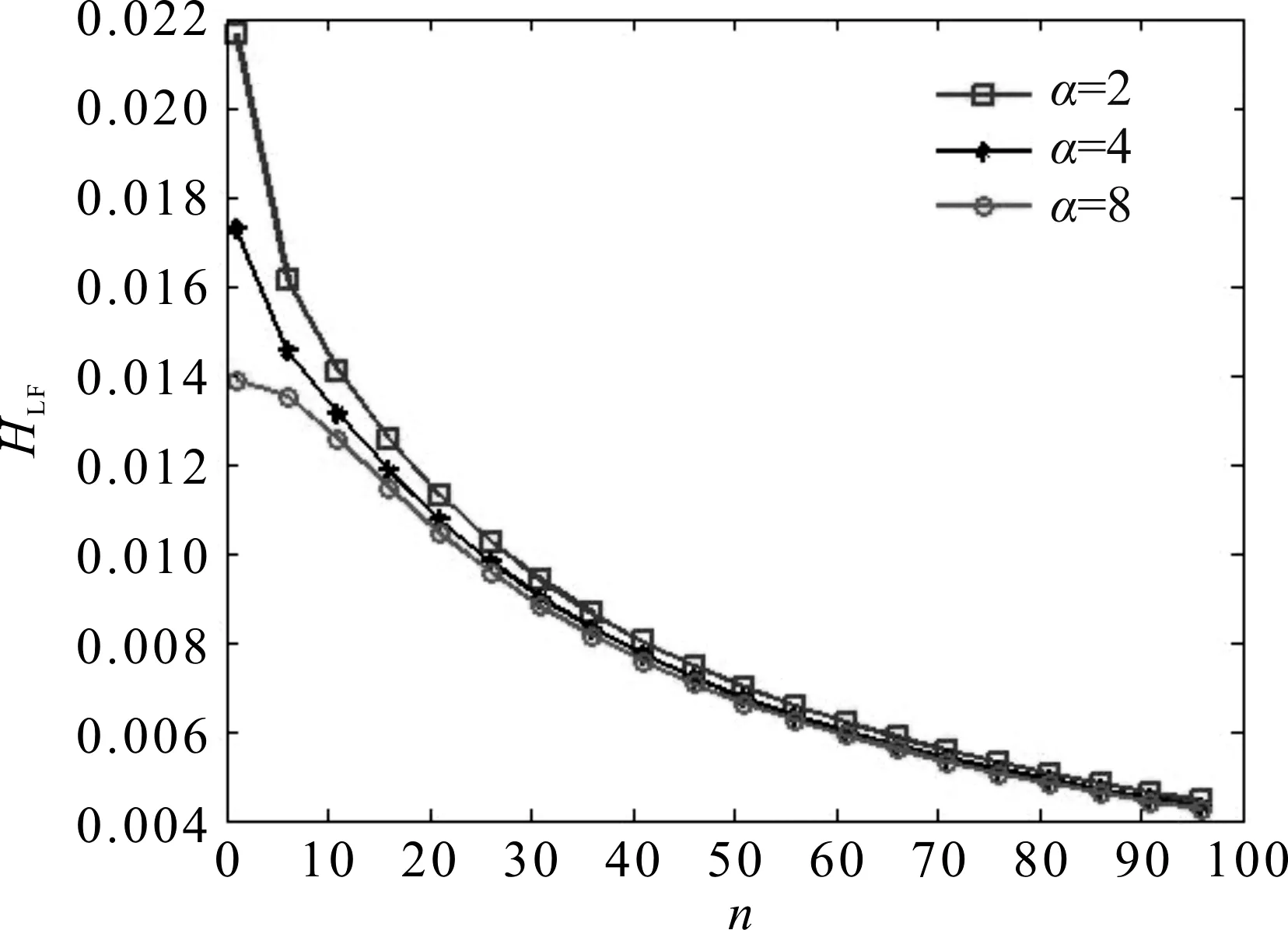
图3 不同领导者数目下，参数n对网络一致性的影响

图4 领导者数目对网络一致性的影响

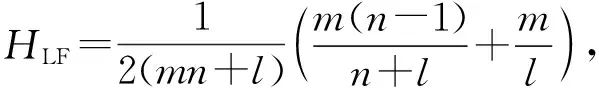
4 结束语

本文应用一类确定性网络计算了具有多个领导者设置的领导-追随者网络一致性。通过网络拓扑结构，精确计算了网络拉普拉斯主子阵的特征谱，由此得到领导-追随者网络一致性的解析表达式，为研究具有多个领导者的多智能体一致性问题提供理论指导。但是，本文研究中，领导者设置在中心节点，下一步考虑将领导者位置设置在其余节点，展开进一步研究与探索。