B样条曲线的双层最小二乘渐进迭代逼近算法
王 慧,邓重阳,李亚娟
(杭州电子科技大学理学院,浙江 杭州 310018)
0 引 言
数据拟合在计算机图形学、计算机辅助设计和计算机辅助制造中均有广泛的应用。在逆向工程领域里,一般是从实物中获取数据点集,然后运用几何方法建立其数字模型[1]。由于这类数据点集的排列往往是不规律的,所以通常选取B样条曲线来拟合这类数据点集。使用B样条曲线拟合数据点时,需要通过求解线性方程组来反算控制顶点。齐东旭等[2]提出均匀3次B样条曲线的盈亏修正算法,Boor[3]证明了算法的收敛性。Lin等[4]先证明了非均匀3次B样条曲线也具有盈亏修正性质,然后将盈亏修正性质推广到所有全正基混合曲线,并给出了渐进迭代逼近的英文术语(Progressive Iterative Approximation,PIA)[5]。对于二维断面数据的曲线重建问题,徐进等[6]提出基于特征点自动识别的3次B样条曲线逼近算法。Lu[7]和Deng等[8]通过调整向量加权的方式,提升了PIA的收敛速度。为了实现用少量控制顶点拟合数据点集,2011年Lin等[9]提出一种扩展的渐进迭代逼近法(Extended Progressive Iterative Approximation,EPIA)。Deng等[10]进一步提出基于最小二乘渐进迭代逼近(Least Squares Progressive Iterative Approximation,LSPIA)的B样条曲线拟合方法,在迭代中计算调整向量并更新控制顶点的位置,从而产生一个曲线序列,其极限曲线序列收敛到关于数据点的最小二乘法所得的曲线。Lin等[11]论证了奇异迭代矩阵LSPIA算法的收敛性。常清俊等[12]提出了分块高斯-塞德尔迭代的曲线曲面拟合方法,与高斯-塞德尔迭代法相比,提升了收敛速度,但这种方法未考虑数据点集中特征点的拟合情形。为了高效且精确地拟合大型数据点集,本文提出一种基于双层LSPIA算法的均匀3次B样条曲线拟合方法,通过相邻点之间拟合圆弧的方法确定特征点,将特征点作为插值点,其余的数据点作为待拟合点,经过双层LSPIA算法,快速生成逼近数据点集的均匀3次B样条拟合曲线。
1 曲线拟合算法
1.1 基于LSPIA的均匀3次B样条曲线拟合算法
(1)
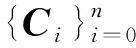
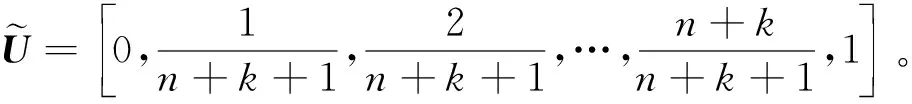
基于LSPIA的均匀3次B样条曲线拟合算法主要步骤如下[10]。
(2)
式中,u∈[t0,tm],基函数对应的配置矩阵为:
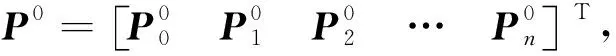
P(0)=AP0
(3)
(2)计算每一个控制顶点的调整向量。
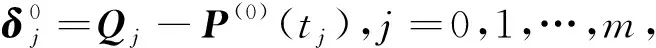
(4)
式中,λ0为矩阵ATA的最大特征值,μ为常数。
(3)更新控制顶点。
(5)
其矩阵形式为:
P(1)=AP1
(6)
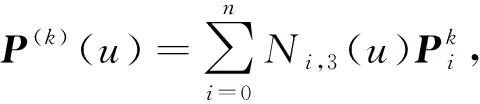
(7)
(8)
(9)
根据新的控制顶点生成第k+1次拟合曲线如下:
(10)
(5)重复执行上述的迭代过程,即可产生一个曲线序列{P(k)(t),k=0,1,2,…}。文献[5]证明了当基函数为全正基函数时,产生的极限曲线序列收敛到关于数据点列的最小二乘拟合结果。
1.2 基于双层LSPIA的均匀3次B样条曲线拟合算法
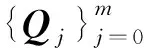
为了更高效地拟合大型数据点集,本文提出基于双层LSPIA的均匀3次B样条曲线拟合算法,算法主要步骤如下。
(1)采用相邻点之间拟合圆弧的方法[6],近似估算每个数据点对应的离散曲率,将数据点列中的曲率极值点、曲率不连续点和曲率拐点作为插值点,同时基于隔点采样法,选取除插值点外数据点列的部分数据点作为拟合点,不妨设插值点误差为ε1,拟合点误差为ε2。
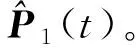
(4)依次执行1.1节中的步骤2和步骤3,得到1次迭代后生成的拟合曲线。

双层LSPIA算法与LSPIA算法相比,在第一层LSPIA算法迭代过程中,构建拟合曲线所含方程的个数等于第一层选取的待拟合数据点的个数,其中基函数的配置矩阵A的维数比LSPIA算法对应的配置矩阵A的维数降低一半左右,因此第一层LSPIA算法的迭代速度更快;虽然第二层LSPIA算法是针对所有数据点进行迭代逼近,但由于均匀3次B样条曲线的局部性质,只要控制顶点位置不变,那么拟合曲线的形状就不会发生改变,即在第二层LSPIA算法迭代过程中,只需迭代更新除第一层待拟合数据点外的其余数据点对应的控制顶点的位置,减少了迭代次数,同时缩短了迭代时间。
2 实例分析
实验平台的操作系统为Windows,测试工具为MATLAB 2017b。实验选取的10个测试数据集是通过提取一些模型的边缘轮廓获得的,对其进行拟合,来验证本文算法的有效性。当数据点和拟合曲线上对应点之间的距离足够小时,认为拟合曲线插值了这一数据点,故将插值点的误差精度和拟合点的误差精度分别设为ε1=10-16和ε2=10-5,即在数值实验过程中,当插值点和拟合点的误差均小于对应的误差精度时,算法迭代停止。分别使用基于LSPIA的均匀3次B样条曲线拟合算法和基于双层LSPIA的均匀3次B样条曲线拟合算法拟合这10组数据集,获得关于数据点集的最小二乘拟合结果。
比较基于LSPIA和基于双层LSPIA的B样条曲线拟合算法的迭代时间与迭代次数,对比结果如表1所示。迭代时间取多次测试时间的平均值,选用平均误差作为拟合误差,表示如下:
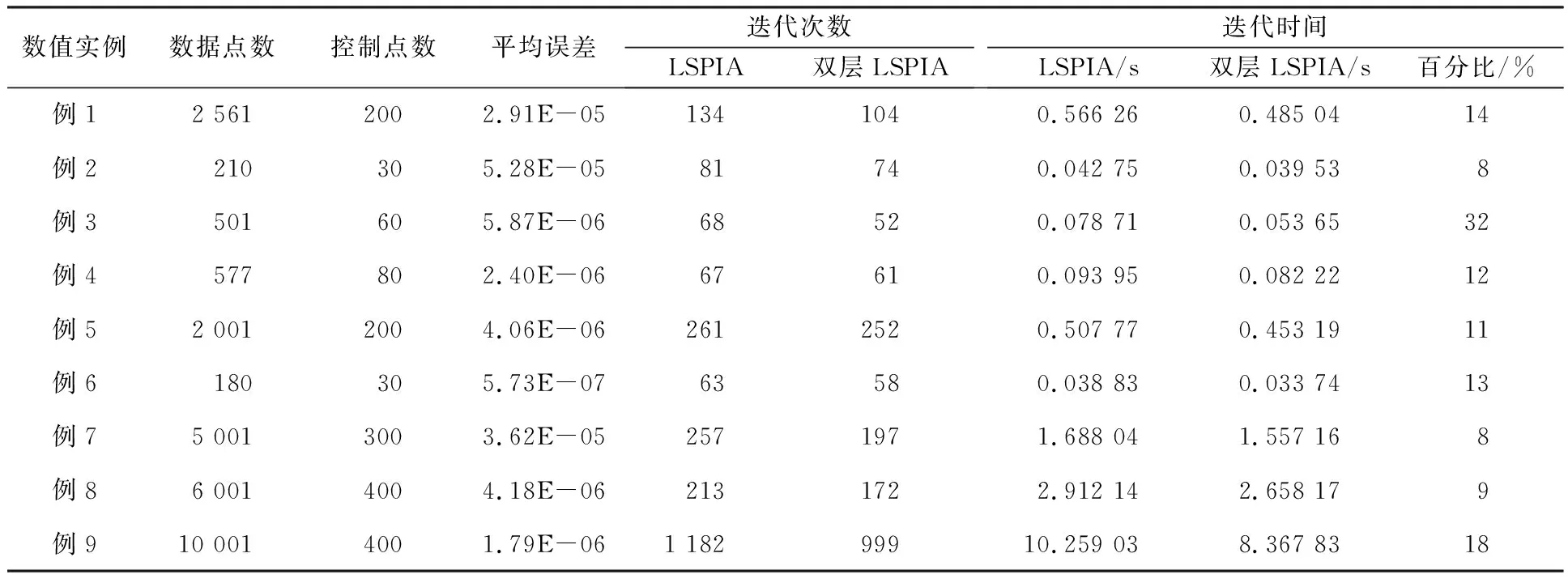
表1 不同方法迭代时间和迭代次数比较
从表1可以看出,无论在迭代时间还是迭代次数上,双层LSPIA算法都比LSPIA算法的拟合效率高,尤其对大量数据点进行拟合时,双层LSPIA算法的迭代时间比LSPIA算法快了约2 s。
图1展示了在相同的误差精度下,分别运用LSPIA算法和双层LSPIA算法拟合例1—例8所需的迭代次数。从图1可以看出,对于数据点数较大且含有较多特征点的数据点集(如例1、例7、例8),双层LSPIA算法的迭代次数明显少于LSPIA算法。
图2给出了LSPIA算法和双层LSPIA算法拟合例9中10 001个数据点集所需的迭代次数随控制顶点数的变化关系。从图2可以看出,在控制顶点相同的条件下,双层LSPIA算法的迭代次数明显少于LSPIA算法,且控制顶点个数为200~500时,两种算法迭代次数的差距较大,展现出本文算法的高效性。综上分析表明,拟合9个数值实例中,双层LSPIA算法所需的迭代次数明显少于LSPIA算法,拟合时间更短。
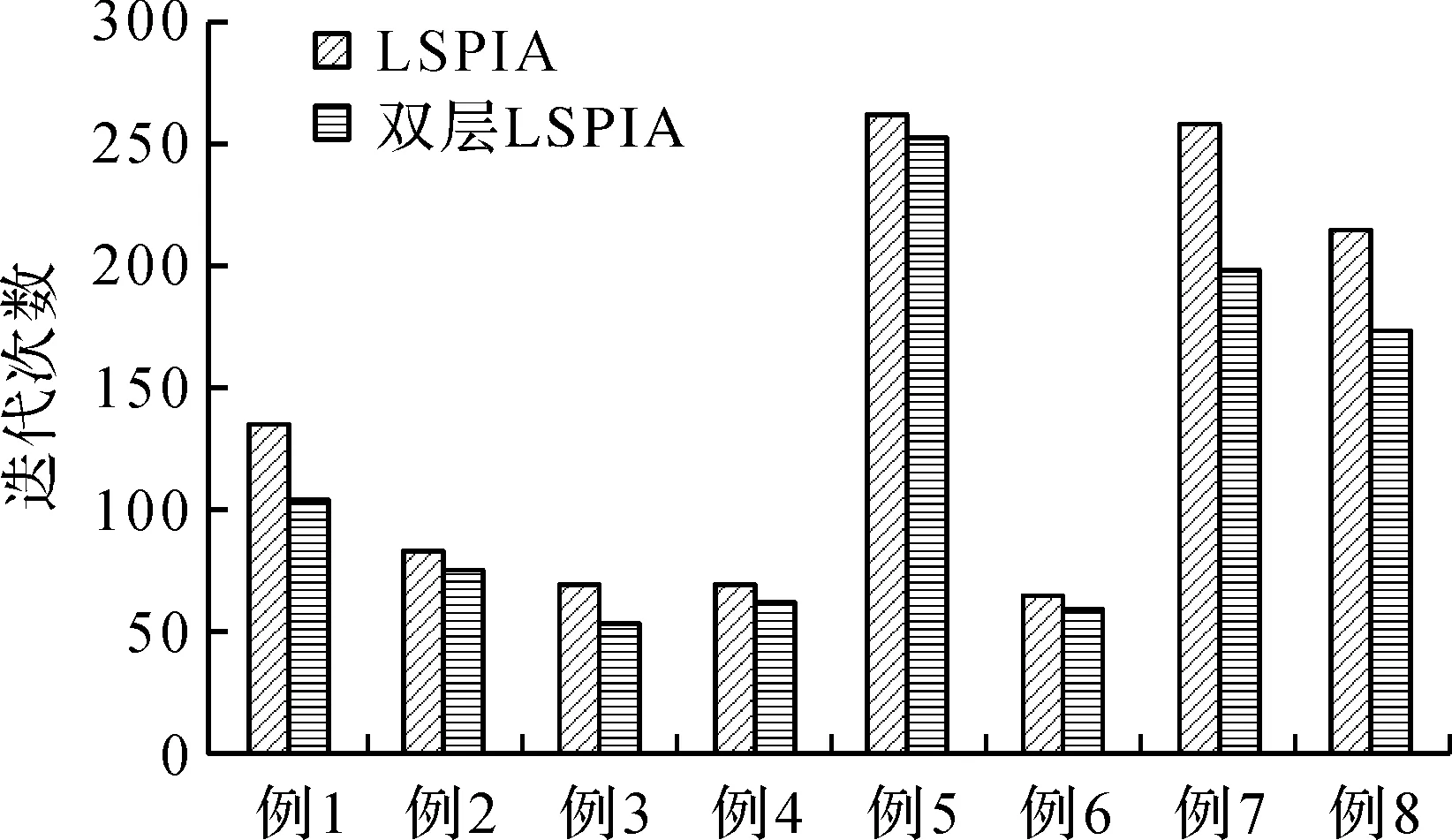
图1 不同方法迭代次数比较
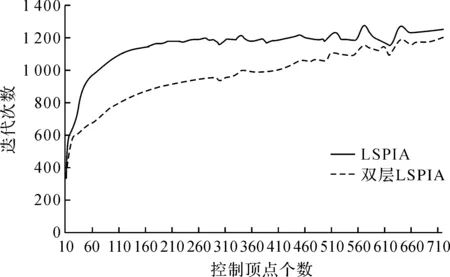
图2 迭代次数随控制顶点数的变化关系
图4展示了采用双层LSPIA算法拟合例2—例9的最终曲线拟合效果,其中实心点为数据点,实曲线是均匀3次B样条曲线的最终拟合效果,矩形框、实线圆和虚线圆分别表示第一层迭代选取的曲率极值点、曲率拐点和曲率不连续点。

图3 拟合2 561个数据点的均匀3次B样条曲线
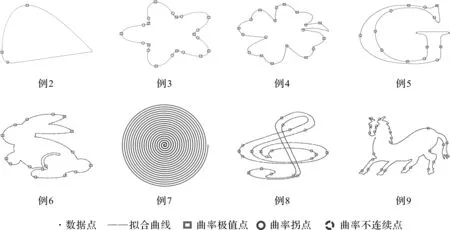
图4 运用双层LSPIA拟合例2—例9的拟合结果
3 结束语
在LSPIA算法的基础上,本文引入分层迭代的思想,将双层LSPIA算法应用于均匀3次B样条曲线拟合中。与LSPIA算法相比,双层LSPIA算法的迭代次数和迭代时间更少,拟合效率更高。后期将研究多层LSPIA的B样条曲线曲面拟合方法,进一步提高误差精度和拟合效率。

