带互异权值的B样条曲线的最小二乘渐进迭代逼近
王曾珍,刘华勇
(安徽建筑大学 数理学院,合肥 230601) E-mail:wangz_z1014@163.com
1 引 言
数据拟合是几何设计中广泛使用的建模工具.曲线的拟合问题通常出现在计算机图形学、计算机辅助几何设计和图像处理等各个领域.渐进迭代逼近法(Progressive Iterative Approximation,PIA)作为一种有效而直观的数据拟合方法,在近几年来受到广泛关注.该方法起源于齐东旭等[1]和de Boor[2]针对均匀三次B-Spline曲线拟合的迭代性质的研究,它不仅可以避免求解大型线性方程组的计算成本,还可以通过对控制顶点进行迭代来调整曲线,直到获得满足误差要求的拟合曲线.蔺宏伟等[3]证明了非均匀三次B样条曲线和曲面也具有PIA这一性质.此外,PIA方法还扩展到了基于NTP基的混合曲线和曲面[4].为加快PIA方法的收敛速度,陆利正[5]提出了一种加权PIA格式(Weighted Progressive Iteration Approximation,WPIA),给出了最优权值取法.陈杰等[6]给出了WPIA的2种推广方法:带权值的局部PIA方法和均匀参数化下的三角Bézier曲面的带权PIA方法.刘晓艳等[7]结合Jacobi迭代法,提出了非均匀三次B样条曲线的渐进迭代插值算法—Jacobi-PIA算法,证明了其收敛速度优于经典的渐进迭代插值算法.张莉等[8]提出一种带互异权值的渐进迭代逼近算法,具有操作灵活且可以根据需要调整各控制顶点的优势.当参数取合适值时,该算法的收敛速度比WPIA算法更快.
在经典的PIA方法中,控制点的数量等于数据点的数量.然而,当数据点的数量非常大时,这是不可行的.因此,Lin等[9]给出了一种扩展的PIA(Extended Progressive Iteration Approximation,EPIA)方法,此方法允许控制点的数量小于给定数据点的数量,但EPIA拟合给定的数据点集时,生成的曲线(曲面)序列的极限不是数据集的最小二乘拟合结果.因此,Deng等[10]提出了一种新的渐进迭代最小二乘方法(progressive iterative approximation for least square fitting,LSPIA),LSPIA通过迭代调整控制点构造一系列拟合曲线(曲面),极限曲线(曲面)是对给定数据点的最小二乘拟合结果.在每次迭代中,每个控制点的差向量是数据点和它们在拟合曲线(曲面)上对应的点之间的差向量的加权和.Lin等[11]证明了最小二乘拟合方程组的系数矩阵为奇异矩阵时,LSPIA方法是收敛的.为保证逼近生成的曲线(曲面)的极限是给定数据点的最小二乘拟合结果,Yusuf Fatihu Hamza等[12]提出一种基于Gauss-Seidel迭代方法的快速PIA算法(GS-LSPIA),该算法比LSPIA算法需要更少的步骤和更短的运算时间,因此收敛速度也得到提高.
此外,近几年来,PIA方法还被扩展至细分格式,如Wang等[13]提出了用于细分曲面插值的Gauss-Seidel几何迭代法(Gauss-Seidel Progressive Iterative Approximation,GS-PIA).最近,Zhang等[14]将PIA方法应用于单帧图像超分辨率重建.
LSPIA方法通过不断调整控制顶点获得一系列拟合曲线(曲面),具备高效、稳定地拟合大规模数据点及显著减少计算量等优点.然而,在LSPIA的迭代过程中,计算差向量时的权值始终为确定范围内的固定值,无法根据需要单独控制部分控制顶点从而调整局部曲线.为使LSPIA方法通过调整权值从而更加灵活地调整局部曲线形状,本文将上述LSPIA方法进行改进,在LSPIA方法的基础上,控制部分数据点的权值不变,赋予其余控制顶点不同的权值,对LSPIA方法和改进后的带互异权值的LSPIA方法进行分析和比较.随后证明本文所提出方法的收敛性.最后给出数值实例,计算出LSPIA和本文所提方法的误差,验证了本文方法的可行性.
2 带互异权值的LSPIA算法
2.1 LSPIA算法描述
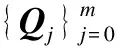
(1)
其中,{Bi(t);i=0,1,…,n}为三次均匀B样条基函数,其配置矩阵为:
(2)
令差向量为:
(3)
且第i个控制顶点的第一个调整向量为:
(4)
其中,权值μ满足0<μ<2/λ0,λ0是矩阵BTB的最大特征值,由此可得新的控制顶点为:
(5)
新的曲线为:
(6)
类似地,假设第k次迭代后获得曲线Pk(t),令:
(7)
(8)
(9)
可得第k+1次迭代后的曲线为:
(10)
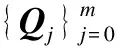
2.2 带互异权值的LSPIA算法
带互异权值的LSPIA算法是在原LSPIA算法[10]上作出的改进.在该算法中,曲线和差向量的表达形式不变,改变调整向量.将1.1节中的LSPIA算法中的常数μ赋予不同的值,即将迭代过程中调整向量(式(8))改为:
(11)
假设已知第k次迭代后的曲线Pk(t),由式(7)和式(11)可得,第k+1次迭代后的控制顶点为:
(12)
第k+1次迭代后得到的曲线为:
(13)
由此可得到一系列迭代逼近曲线{Pk(t),k=0,1,…}(k为迭代次数).当μi都取相同值且满足0<μ<2/λ0时,则改进的算法退化为LSPIA算法.
3 带互异权值的LSPIA算法的收敛性
本节将证明,当μi满足一定条件时,上述带互异权值的LSPIA算法是收敛的,且极限曲线为初始数据点的最小二乘拟合曲线.
定理2.当μi满足条件0<μ<2/λ0,那么带互异权值的LSPIA算法是收敛的.
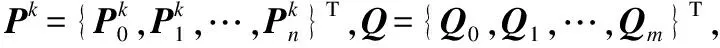
(14)
根据式(9)和式(11)可得:
(15)
将式(15)写成矩阵形式:
Pk+1=Pk+AT(Q-BPk)
(16)
其中A=UB,B为三次均匀B样条基函数的配置矩阵.
令D=I-ATB,I为n+1阶单位矩阵,由式(16)可得:
Pk+1=Pk+AT(Q-BPk)=
(I-ATB)[Pk-(ATB)-1ATQ]+(ATB)-1ATQ
(17)
则:
Pk+1-(ATB)-1ATQ=(I-ATB)[Pk-(ATB)-1ATQ]=
(I-ATB)2[Pk+1-(ATB)-1ATQ]=…=Dk+1[P0-(ATB)-1ATQ]
(18)
设{λi(D)(i=0,1,…,n)}是按非递减顺序排列的D的特征值.令λi(D)=1-λi,其中λi是按非递减顺序排列的ATB的特征值.
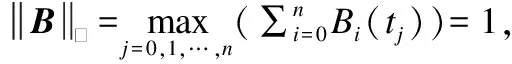
根据式(18)可得:
P∞=(ATB)-1ATQ+D∞[P0-(ATB)-1ATQ]=(ATB)-1ATQ
(19)
式(19)等价于(ATB)P∞=ATQ,意味着带互异权值的LSPIA算法是收敛的,且极限曲线收敛到初始数据点的最小二乘拟合结果.
4 数值实例
在实例分析这一部分,本文选取一般的三次均匀B样条曲线拟合给定点集.通过实验调整常数μ的取值来控制曲线形状的变化,μ值改变后对应的控制顶点随之变化,进而可以调整局部曲线的形状,并观察初始拟合曲线和本文提出算法迭代后的拟合曲线改变局部形状后的变化.
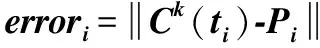
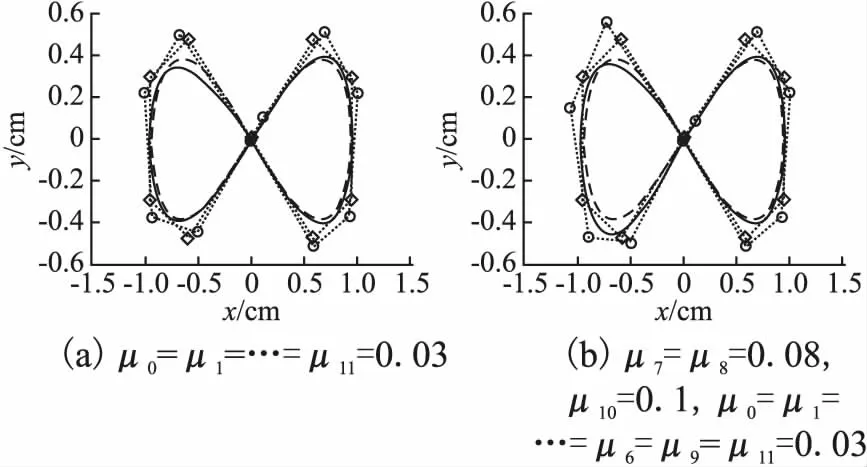
图1 μ取不同值时LSPIA的逼近双纽线Fig.1 Approximation lemniscate of LSPIA with different values
例1.在双纽线p(t)=(x(t),y(t))=(cost,sint·cost)上选取11个点p(ti)=(x(ti),y(ti))(ti=-π/2+i·π/5,i=0,1,…,10)作为初始控制顶点,迭代次数为k=15.图1(a)为μ取相同值0.03时依据LSPIA方法将控制顶点迭代15次后,三次均匀B样条曲线逼近本例中所取11个控制顶点连接的控制多边形所得到的曲线图.观察图1(a)迭代结果,将第7、第8和第10个控制顶点进行调整,根据实验值,令μ7=μ8=0.08,μ10=0.1,图1(b)为调整后的曲线图.可见,调整后的图1(b)中迭代后的逼近曲线与位于图中左下部分第7、8个初始控制顶点的距离更近,局部曲线得到调整.

表1 例1中调整第i个控制顶点前后的逼近误差Table 1 Approximation errors before and after adjusting the ith control vertex in example 1
表1为μ0=μ1=…=μ11=0.03和μ7=μ8=0.08,μ10=0.1,μ0=μ1=…=μ6=μ9=μ11=0.03时,第7、第8和第10个控制顶点调整前后的逼近误差.根据图表所示,误差减小,说明依据本文提出方法进行局部调整后的逼近性更好.
例2.在圆弧p(t)=(x(t),y(t))=(sint,cost)上选取11个点p(ti)=(x(ti),y(ti))(ti=7π/6+i·π/6,i=0,1,…,10)作为初始控制顶点,迭代次数k=20.图2(a)为μ取相同值0.5时依据LSPIA方法将控制顶点迭代20次后,3次均匀B样条曲线逼近本例中所取11个控制顶点连接的控制多边形所得到的曲线图.观察图2(a),第10个控制顶点附近所对应的局部曲线逼近效果不佳,因此依据本文所提出方法调整对应控制顶点的位置,令μ10=0.01,得到图2(b).

图2 μ取不同值时LSPIA的逼近圆弧Fig.2 Approximation arc of LSPIA with different values
表2为μ0=μ1=…=μ11=0.5和μ10=0.01,μ0=μ1=…=μ9=μ11=0.5时,第10个控制顶点调整前后的逼近误差.
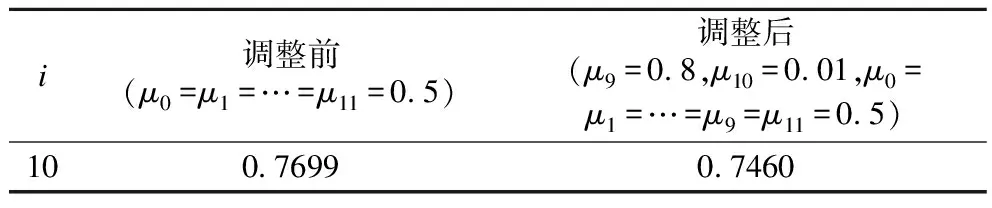
表2 例2中调整第i个控制顶点前后的逼近误差Table 2 Approximation errors before and after adjusting the ith control vertex in example 2
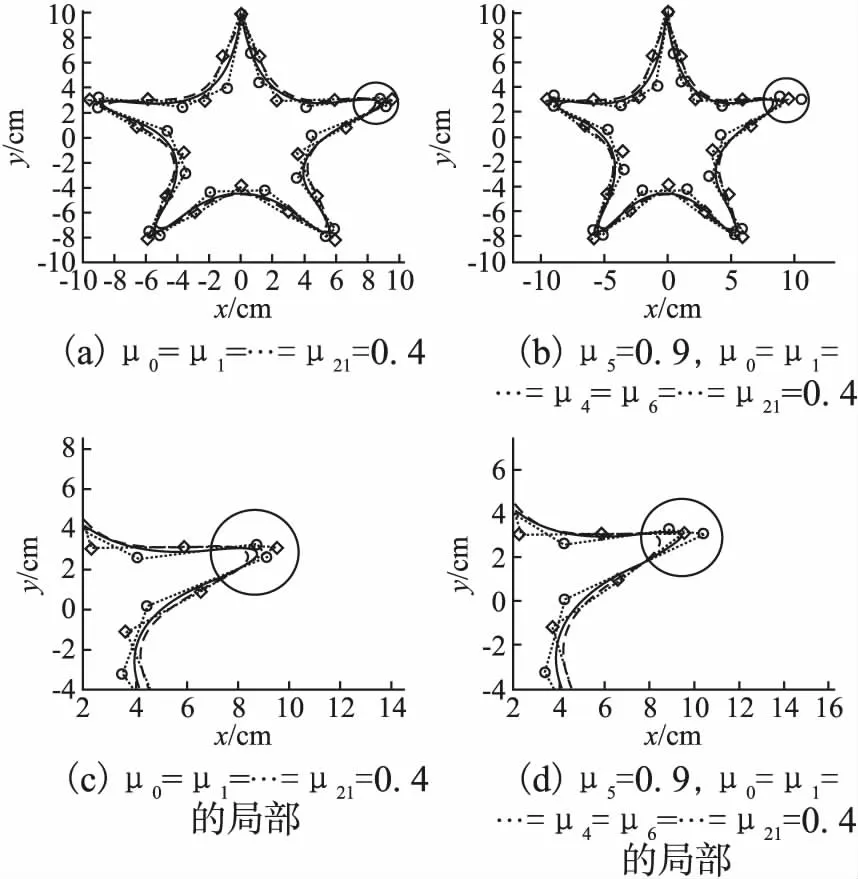
图3 μ取不同值时LSPIA的逼近五角星Fig.3 Approximate five-pointed star of LSPIA with different values
例3.在五角星上选取21个点作为初始控制顶点:(6.1232×10-16,10),(1.1226,6.5451),(2.2451,3.0902),(5.8779,3.0902),(9.5106,3.0902),(6.5716,0.9549),(3.6327,-1.1803),(4.7553,-4.6353),(5.8779,-8.0902),(2.9389,-5.9549),(-7.0166×10-16,-3.8197),(-2.9389,-5.9549),(-5.8779,-8.0902),(-4.7553,-4.6353),(-3.6327,-1.1803),(-6.5716,0.9549),(-9.5106,3.0902),(-5.8779,3.0902),(-2.2451,3.0902),(-1.1226,6.5451),(6.1232×10-16,10),迭代次数为k=5.图3(a)为μ取相同值0.4时依据LSPIA方法将控制顶点迭代5次后,三次均匀B样条曲线逼近本例中所取21个控制顶点连接的控制多边形所得到的曲线图.根据图3(a)结果,利用本文所提出方法调整第5个控制顶点,令μ5=0.9,其余μ的取值不变,仍迭代5次后得到逼近曲线图3(b),将五角星的右上角调整后,逼近曲线近似插值第5个控制顶点.图3(c)为图3(a)的局部放大图,图3(d)为图3(b)的局部放大图.
表3为μ0=μ1=…=μ11=0.4和μ5=0.9,μ0=μ1=…=μ4=μ6=…=μ21=0.4时,第5个控制顶点调整前后的逼近误差.

表3 例3中调整第i个控制顶点前后的逼近误差Table 3 Approximation errors before and after adjusting the ith control vertex in example 3
例4.在曲线p(t)=(x(t),y(t))=(t,sint)上选取15个点p(ti)=(x(ti),y(ti))(ti=i·π/7,i=0,1,…,14)作为初始控制顶点,迭代次数为20次.图4(a)为μ取相同值1.5时依据LSPIA方法将初始控制顶点迭代20次后,三次均匀B样条曲线逼近本例中所取15个控制顶点连接的控制多边形所得到的曲线图.图4(b)为依据本文提出方法调整第4个控制顶点对应的权值μ4=0.001,保持其余μ值不变所得到的正弦曲线逼近图.图4(c)为4(a)的局部放大图,图4(d)为图4(b)的调整局部放大图.
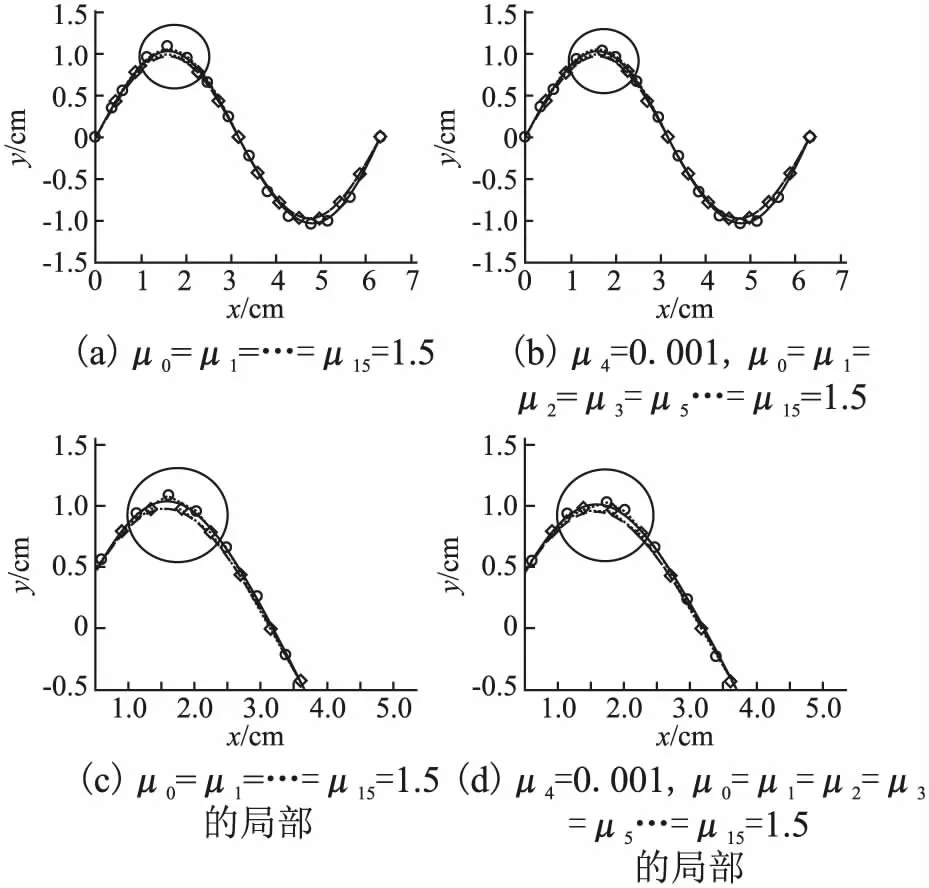
图4 μ取不同值时LSPIA的逼近正弦曲线Fig.4 Approximation sinusoidal curve of LSPIA with different values

表4 例4中调整第i个控制顶点前后的逼近误差Table 4 Approximation errors before and after adjusting the ith control vertex in example 4
表4为μ0=μ1=…=μ15=1.5和μ4=0.001,μ0=μ1=μ2=μ3=μ5…=μ15=1.5时,第4个控制顶点调整前后的逼近误差.
5 结 语
本文在权值相同的LSPIA算法的基础上,提出带互异权值的LSPIA算法.给出权值取值范围,证明权值在该范围内取值时带互异权值的LSPIA算法的收敛性.根据LSPIA算法结果调整不同控制顶点对应的权值,对曲线进行局部调整.实例结果表明,调整后的局部曲线逼近误差减小,达到调整局部曲线逼近效果的目的.本文依据LSPIA实验结果选取需要调整的权值,所给出权值为本文所提出方法迭代收敛范围内的实验值.因此,在权值选取和误差控制范围这方面仍待研究.

