基于重新参数化技术的新Cusa-Huygens不等式
陈小雕,姜霓裳
(1.杭州电子科技大学计算机学院,浙江 杭州 310018;2.杭州电子科技大学理学院,浙江 杭州 310018)
0 引 言
不等式的估算及其证明在通信等领域有着较为广泛的应用。对Cusa-Huygens不等式的研究引起学者们广泛的兴趣,包括逼近函数采用由cos(x)和sin(x)组成的有理形式的函数[1-5],或采用由sin(x)和tan(x)组成的非有理形式的函数[6-12]。逼近函数形式越简单、逼近误差越小,对应不等式得到的应用更好更广泛。Cusa-Huygens不等式研究方面,大部分集中在逼近误差或逼近阶的改进[13-16]。相当条件下,对应不等式的误差越小,越有可能得到更好更广泛的应用。为了进一步改善逼近误差或提高逼近效率,本文讨论了结合Padé逼近和重新参数化技术的方法,在相当条件下可以获取比已有方法更小的逼近误差。
1 Cusa-Huygens不等式及改进
2018年,Zhu[15]提出更正后的Frame不等式:
(1)
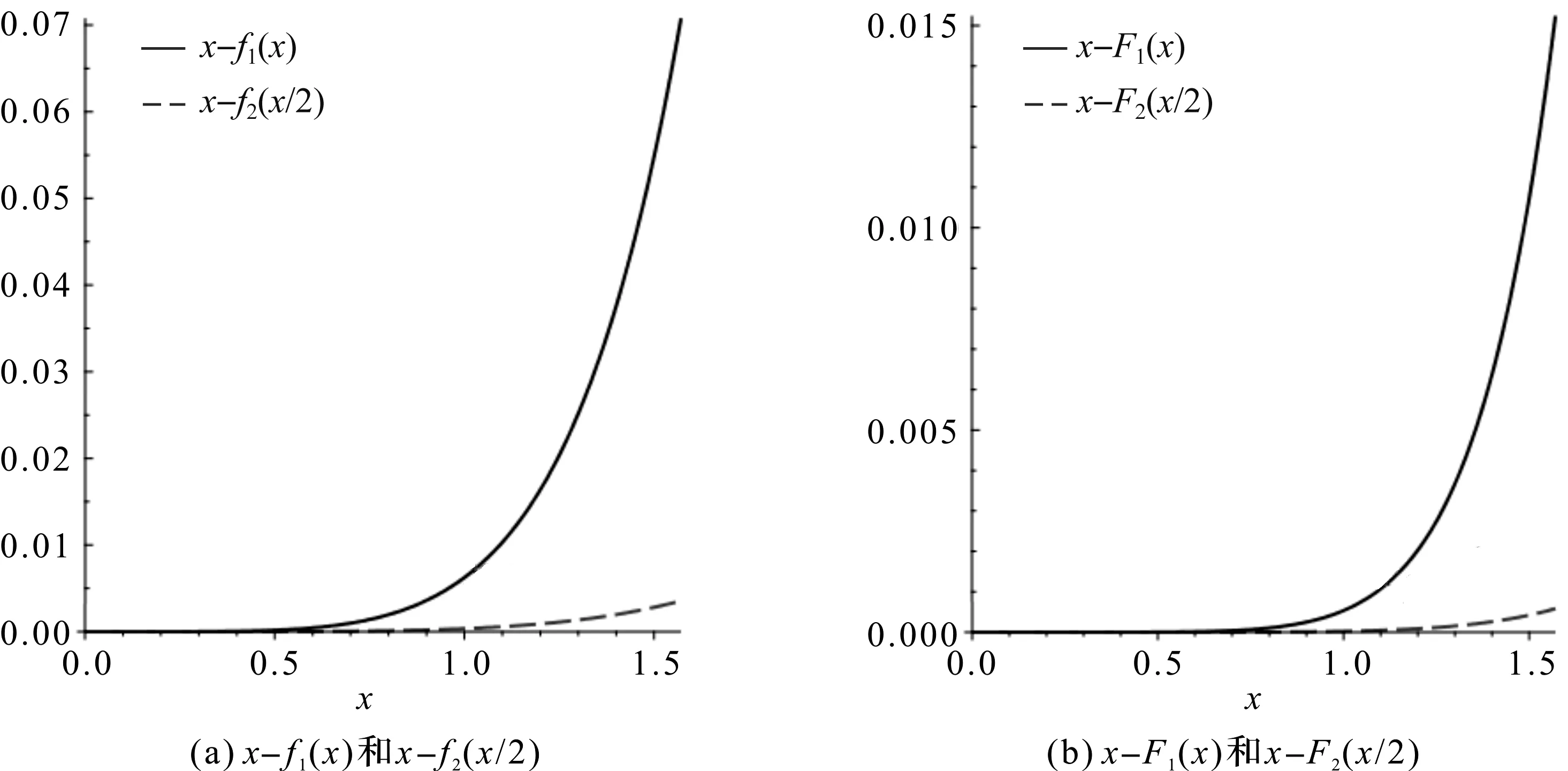
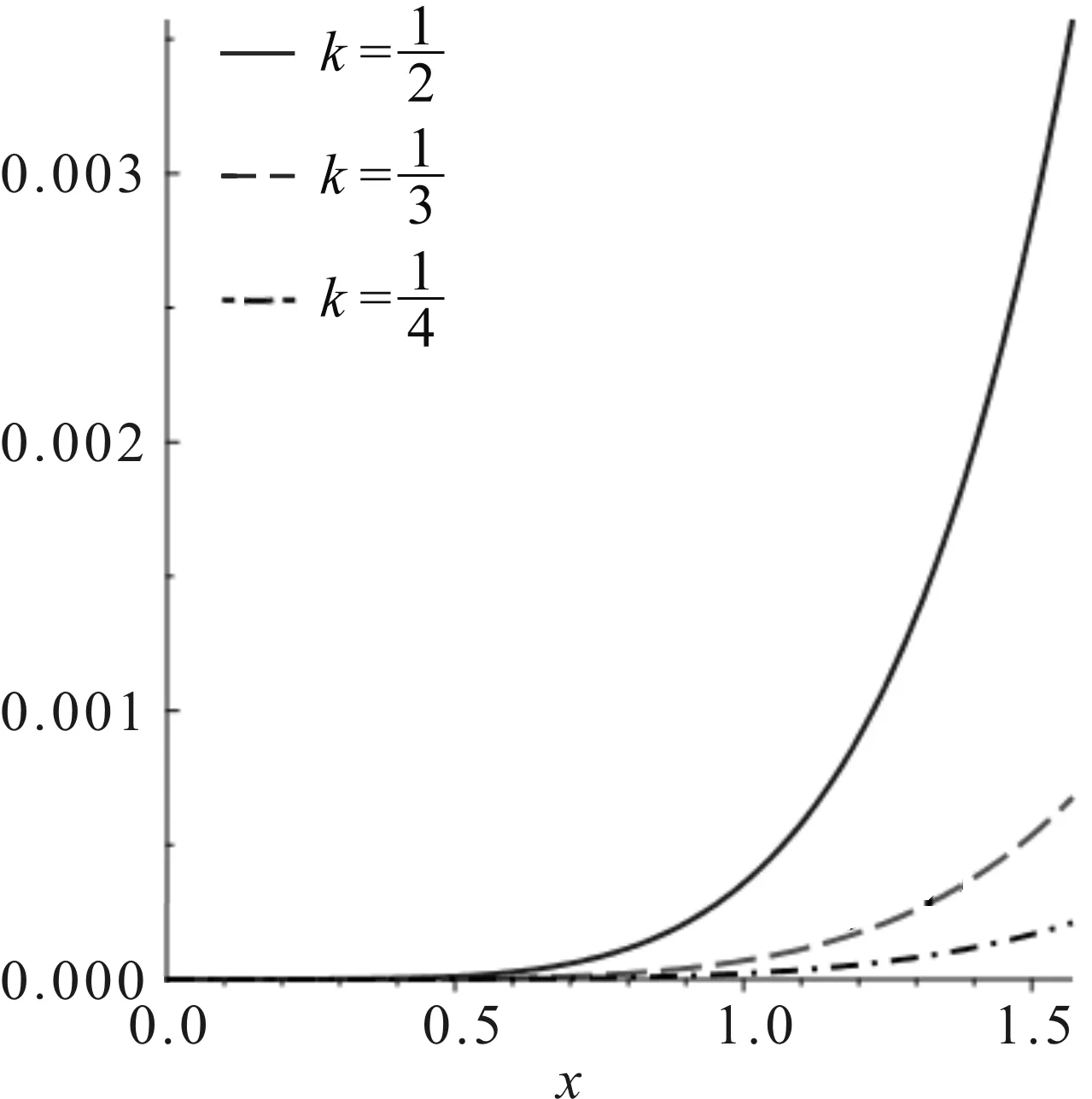
2019年,Zhu[16]发表了具有上下边界条件的不等式,即对于∀0 (2) (3) 式中,常数m1≈92.964,m2≈899.040。 本文结合Padé逼近与重参数化方法的思路,采用Padé逼近技术,将式(1)—式(3)中的边界函数一般化,得到以下的函数形式: 令 可得δ(0)=δ″(0)=0。求解下列2个约束方程 δ′(0)=δ(3)(0)=0 (4) 可以得到a=3,b=2,即式(1)中的f1(x)。 令 易得δ1(0)=δ1″(0)=0,通过解约束式(4),得到a=6,b=2,即 通过求解 (5) 记函数R1(x),Ri(x),α1(t),α2(t), (6) α1(t)=7cos3(t)+294cos(t)+644 (7) α2(t)=2cos4(t)+4cos3(t)+81cos2(t)+448cos(t)+410 (8) 为方便说明,令 其中s0是方程s3+2s2+92s-32=0在[0,1]上的实根。 由式(6)—式(8),可得: (9) 同时可以验证得到 (10) 将文献[16]的引理2和引理3综合成如下引理。 引理1[16]对于t∈(0,π],函数 引理2下列不等式成立 (11) 从式(11)可得,R4(t)在区间(0,t1]单调递增,即∀0 引理3在区间(0,π/2]内存在唯一解t1,使得 (12) 另一方面,由于α2(t)>0,(0 于是,得到本文的主要结论。 定理1对于x∈(0,π],存在下列不等式 (13) 证明令x=2t,易得 (14) 将引理1和式(14)联立,可以得到 (15) 由式(14)和式(15),可以直接得到定理1中的不等式(13),定理1得证。 定理2对于x∈(0,π],存在下列不等式 (16) 证明结合引理2和引理3,通过数值计算可以得到 式(2)和式(3)中,f1(x)和F1(x)为研究人员得到的逼近结果,式(13)和式(16)中f2(x)和F2(x)为基于本文结合Padé逼近与重参数化方法的思路得到的逼近结果。理论上,Padé逼近更方便确定逼近函数的表达式;而重新参数化技术可进一步提高对应的逼近阶,得到更好的逼近效果。根据式(2)和式(3)、式(13)和式(16)分别绘制x-fi(x)和x-Fi(x)的误差曲线如图1所示,其中i=1,2。从图1可以看出,图1(b)取得了更好的逼近效果。 图1 采用不同方法得到的误差曲线 图2 x-φ(x,k)不同的k对应的误差曲线 本文讨论了Cusa-Huygens不等式,并对其进行了改进。重新参数化技术可以调整函数的导数,使得逼近函数满足预定的导数,从而提高相应的逼近阶,获取更好的逼近效果。后续将使用其他单调递增函数作为新的重新参数化函数。本文思路可望被应用到更多类型的三角函数不等式中,以获取更多包围盒更为紧凑的新不等式。
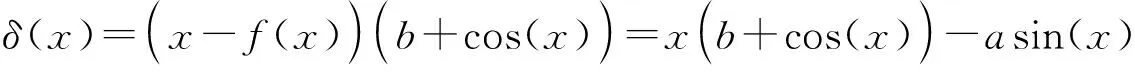
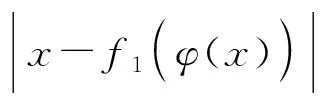
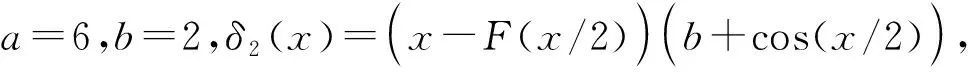
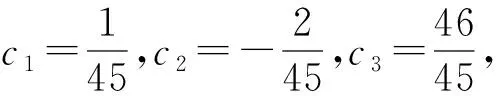
2 主要结论

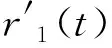


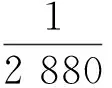

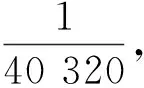

3 结束语

