大规模MIMO系统的自适应阈值信道估计算法

孙文胜，马天然

(杭州电子科技大学通信工程学院，浙江 杭州 310018)

0 引 言

大规模多入多出(Multiple-Input Multiple-Output, MIMO)系统通过配备大数量级天线以提高多路复用的能效，具有可靠性高、无线系统容量大等特点，是5G发展的关键技术之一[1]。正确的信道状态信息(Channel State Information，CSI)是充分发挥大规模MIMO优势的前提条件。在大规模MIMO系统中，由多个天线引起的多载波信号叠加特性使得信道估计变得困难，并且下行链路信道的CSI只能通过接收器来估计[2]。在实际MIMO正交频分复用(Orthogonal Frequency Division Multiplexing，OFDM)系统中，信道状态信息的获取需要通过信道估计技术来完成，传统的信道估计方法主要分为盲信道估计、半盲信道估计以及基于导频的信道估计方法[3]，基于导频的信道估计易实现，应用广泛。

近年来，用户信道矩阵在多小区多用户MIMO系统中具有隐藏稀疏特性[4]，故引入压缩感知(Compressed Sensing，CS)技术进行信道估计。稀疏信号从高维“压缩”到低维变成测量向量，根据筛选条件选择出较好的观测向量从而恢复原信号[5]。经典的贪婪重构恢复算法有正交匹配追踪(Orthogonal Matching Pursuit，OMP)算法[6]、正则化正交匹配(Regularized OMP，ROMP)算法[7]以及广义正交匹配追踪(Generalized OMP，GOMP)算法[8]，这几种算法恢复信号时都需要借助于信号的稀疏度信息。但在实际应用中，信道的稀疏度是一个不确定信息，对算法的重构精度有所影响。文献[9]提出一种分段正交匹配追踪(Stagewise Orthogonal Matching Pursuit，StOMP)算法，无需确定信号稀疏度既可较为准确地恢复信号，但是算法的阈值选择具有人为性，降低了不同场景下的重构效率。通过对压缩感知重构算法深入研究发现，原子挑选阈值和迭代停止条件对信号重构效率有直接影响。文献[10]提出一种改进GOMP算法，根据每次迭代随机生成的概率值与设定概率值的对比结果来决定原子挑选的方式。文献[11]采用二次筛选和变步长选择方式进行原子的挑选。文献[12]在每次迭代时选取或删除合适数量的原子。文献[13]改进了压缩采样匹配追踪(CompressiveSampling MP，CoSaMP)算法中衡量向量系数相关性的判定方式，提高了估计精度。文献[14]将相邻迭代感知矩阵和残差之间的相关度变化量作为迭代停止条件，提高了算法的效率。StOMP算法运用在不同场景时其阈值需要多次训练，同时在低信噪比信号下重构精度较差，为此，本文基于StOMP算法，通过改进算法的阈值设置，进而提出一种自适应双阈值的比例积分微分-分段正交匹配追踪(Proportion Integral Derivative-StOMP, PID-StOMP)算法。

1 大规模MIMO系统模型

1.1 压缩感知理论

压缩感知技术就是运用信号的稀疏性质或在某个变换域上可压缩的特点，用信息采样代替信号采样并从随机映射的观测值中获取有效信号的过程。其数学模型表示如下：

y=Ψx

(1)

式中，y∈RM×1是观测向量，表示对M个观测数据进行观测；x∈RN×1是原信号(M≪N)；Ψ∈RM×N是测量矩阵。压缩感知要求信号为稀疏的，因此需要将无线传输的信道信号通过一个矩阵映射到稀疏空间，即通过傅里叶变换到频域空间上进行压缩，其稀疏表达式如下：

x=Φθ

(2)

式中，Φ∈RM×N是变换矩阵，θ∈RN×1是原信号x在变换域的表达，若其中非零元素的个数K远小于原始信号长度N，则称其为K稀疏信号。而θ中所有非零元素构成的列集合即为支撑集，记作supp(θ)。这样，信号x就经过正交基矩阵变换为在Φ域内稀疏的信号。

根据式(1)和式(2)，重构信号模型描述为：

y=ΨΦθ

(3)

1.2 大规模MIMO系统信道模型

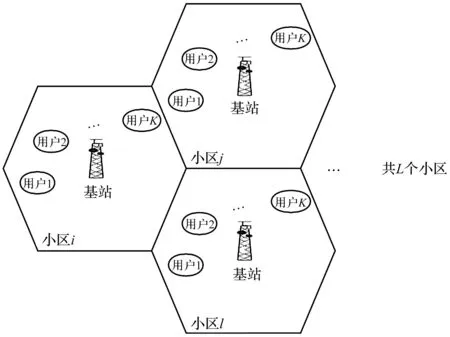
图1 大规模MIMO系统模型

本文采用的系统模型是多小区大规模MIMO-OFDM系统模型，共设置L个小区，每个小区设置中心基站并配有M根均匀排列的发射天线，服务于小区中K个同时通信的移动用户，即信号的稀疏度为K，其系统模型如图1所示。

图1所示的系统模型下，第i(i=1,2,…,L)个小区中第j个(j=1,2,…,K)用户接收到的信号yij∈RM×i表示为：

yij=Hijxj+ni

(4)

式中，Hij∈RM×K表示第i个小区中第j个用户接收到的信道矩阵，一般由无线信道的衰落情况来决定；xj∈RK×1是用户发射的训练序列；ni∈RM×1是小区内用户接收到的高斯白噪声，其均值为0，方差为σ2。

用矩阵形式来表示第i个小区接收的信号：

Y=HiXi+Ni

(5)

式中，Hi=[H1iH2i…HKi]是I个小区中所有的用户信道组成的信道矩阵；Xi=[X1X2…XI]T是这I个小区发送的训练信号矩阵。

由于信号在传播过程中的衰落特性，使得信道矩阵在频域空间中表现出稀疏特性，因此可以通过压缩感知的方式来估计信道。

2 自适应双阈值比例积分微分-分段正交匹配追踪算法

分段正交匹配追踪算法StOMP是基于OMP算法改进的一种自下而上的贪婪算法，先预设1个可能解，再通过迭代来逼近全局最优解。在每次迭代时，首先计算传感矩阵与上次迭代残差的内积，从中筛选出符合设置门限的多个原子，更新候选原子集合；然后求解最小二乘解的同时记录当前残差。与普通的OMP算法相比，迭代时，StOMP算法一次性选择多个原子，减少了迭代次数，加快了计算速度。但是，由于其阈值参数和迭代次数的设置都是凭人为经验设置的，每次迭代重构出的信号可能与原信号有一定误差，降低了重构精度[15]。针对这个问题，本文改进了分段正交匹配追踪算法，提出一种自适应双阈值的比例积分微分-分段正交匹配追踪算法PID-StOMP。

首先，改进原子的挑选阈值。引入比例-积分-微分(Proportion-Integral-Derivative，PID)思想，当一个系统的参数无法有效确定时，PID算法将计算值与预设值进行比较，对所得误差进行比例、微分、积分运算，再反馈到输入值重新调整参数，直到误差符合预设误差的范围[16]。

常规的PID连续控制微分方程用比例系数Kp、积分时间常数Ti和微分时间常数Td表示：

(6)

式(6)中，微分单元和积分单元都要求输入误差是连续值，根据多小区多用户的系统模型可知，所得重构信号的误差值一般为离散的，则离散化表示迭代的门限阈值u：

(7)

由于此时的误差调整需要遍历之前所有的误差状态，对系统的存储容量和计算能力提出较高的要求，因此，引入增量型计算误差值，使得当前迭代阈值无需累加，从而提高了算法的可行性。增量化表示如下：

Δut=ut-ut-1=KpΔet+Kiet+Kd[Δet-Δet-1]

(8)

式中，Δet=et-et-1，应用于PID-StOMP算法中的动态变化阈值参数表达为：

ut=Kp(et-et-1)+Kd(et+et-2-2et-1)+Kiet

(9)

然后，改进迭代停止条件。迭代终止次数的设置需要以信噪比作为先验知识。实际环境中，信噪比是未知的，应用范围受限。PID-StOMP算法通过引入残差能量的阈值判决来提高重构精度，但是，因为残差能量中有一部分能量属于噪声能量，在较低信噪比情况下，噪声能量占据残差能量的绝大部分，因此考虑在低信噪比条件下，对式(4)进行如下修改：

(10)

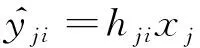
(11)

(12)

当迭代次数不断累加，残差能量的变化主要由随机噪声能量引起。为了消除信号带宽外的随机噪声分量对迭代状态的影响，将式(12)和式(13)相减，得到如下迭代终止判决条件：

(13)

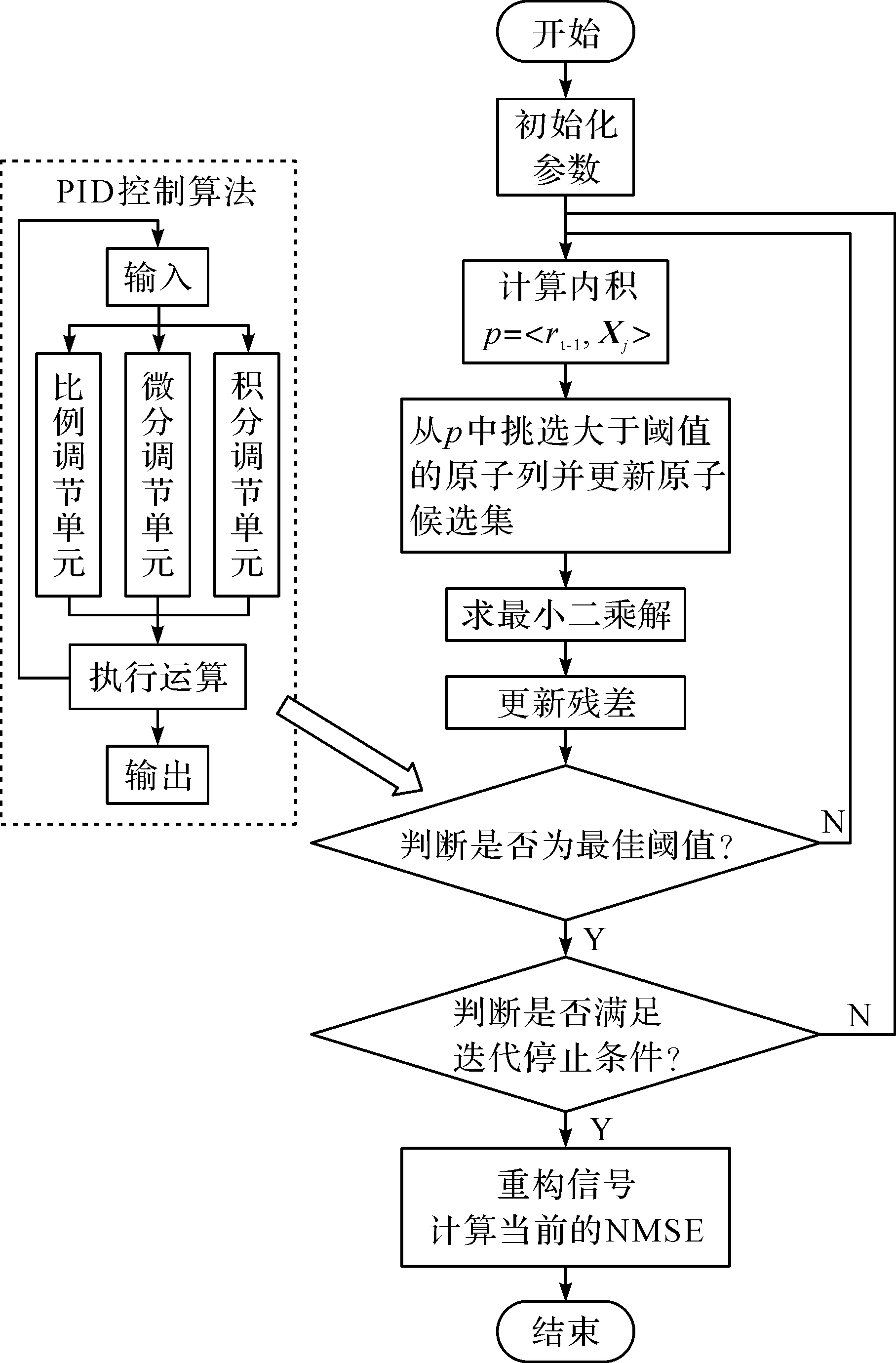
图2 PID-StOMP算法流程图

本文重构信号的误差采用归一化均方误差(Normalized Mean Square Error, NMSE)作为算法的误差判断方式，其表达式如下：

(14)

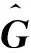
PID-StOMP算法的流程如图2所示。

3 仿真实验及分析

为了验证本文提出的PID-StOMP算法在大规模MIMO系统中用于信道估计的有效性，在MATLAB 2015b平台上仿真模拟TDD工作模式下的下行信道。

仿真采用5个相邻的宏蜂窝小区系统，单个小区半径为1 km，基站位于小区中心并均匀排列着128根天线。PID-StOMP算法参数设置如表1所示。实验中，为了真实反映重构精度的提升并非阈值选择范围扩大或减小所致，所有算法的阈值搜索范围均设置为[2.0,3.0]。

表1 PID-StOMP算法参数说明

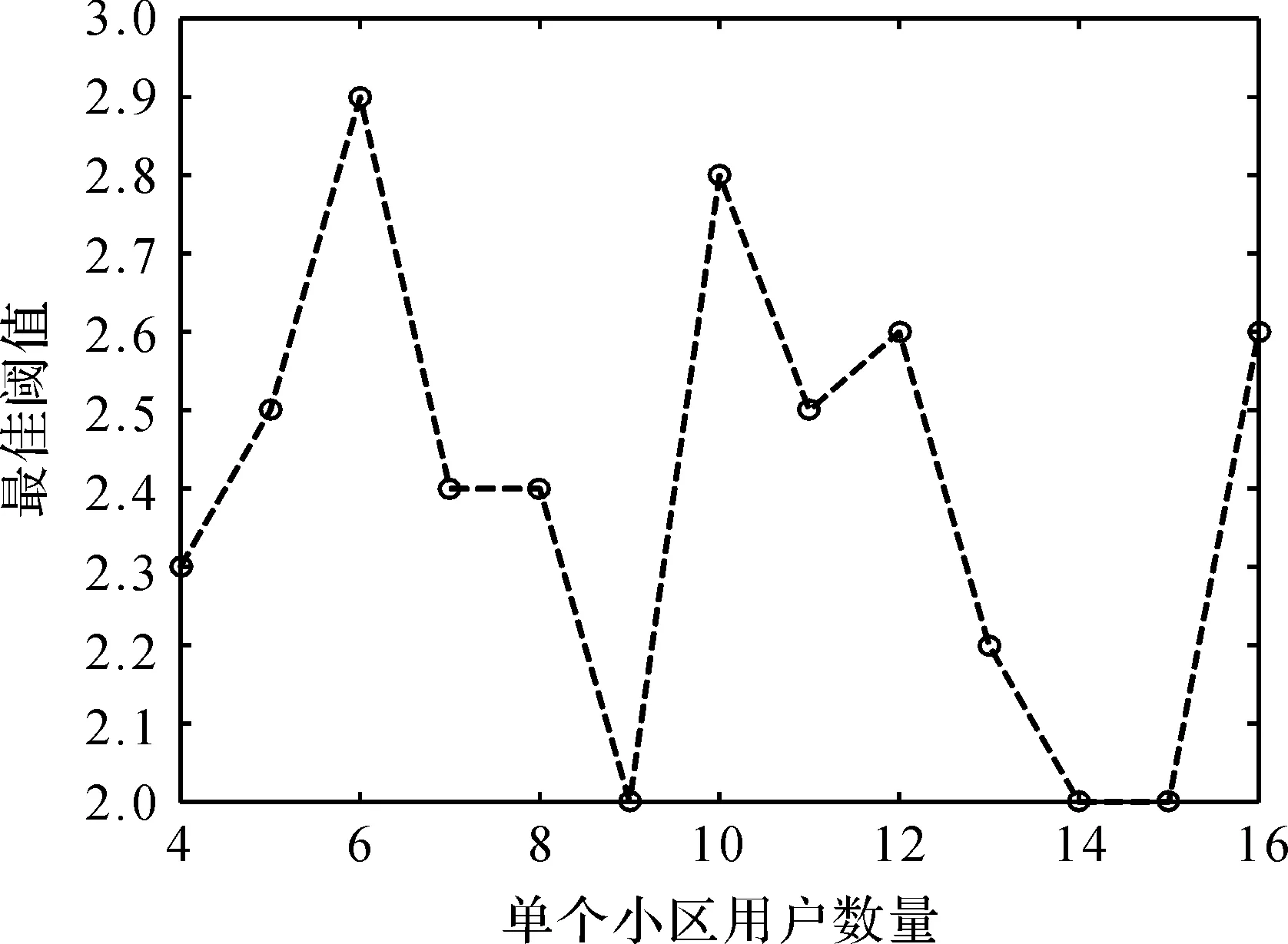
图3 PID-StOMP算法搜索得到的最佳阈值

根据小区内不同的用户数量，采用PID-StOMP算法重构信号，在误差最小的情况下，运用PID-StOMP算法搜索出的最佳挑选原子阈值不尽相同，结果如图3所示。从图3可以看出，当小区用户数发生变化时，挑选原子的最佳阈值并不是固定的，若采用固定阈值则无法使得恢复信号与原始信号间的误差最小，从而降低了估计精度。

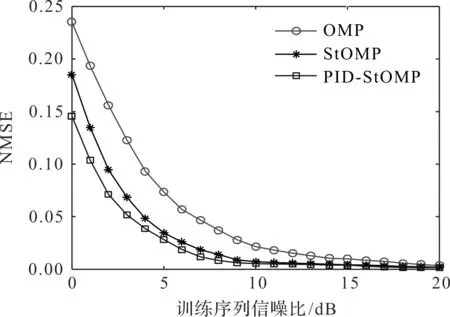
图4 小区用户数为5时，不同算法的估计性能

当单个小区用户数为5时，分别采用OMP算法、StOMP算法(其固定阈值为2.5)及PID-StOMP算法进行信道估计，得到3种算法的估计性能结果如图4所示。从图4可以看出，在0～5 dB低信噪比情况下，NMSE相同时，比较3种算法的训练序列信噪比性能，StOMP算法比OMP算法大约提升了1.0～2.0 dB；PID-StOMP算法比StOMP算法大约提升了0.2～0.8 dB。以同样的方式观察，当信噪比为6～20 dB时，PID-StOMP算法和StOMP算法的估计性能近似重合，这是因为当小区用户数为5时，由图3得到的PID-StOMP算法的最佳原子挑选阈值为2.5，与StOMP算法的固定阈值一致。在低信噪比下，PID-StOMP算法的估计误差低于StOMP算法，体现了PID-StOMP算法在迭代停止判决阶段的阈值优势。

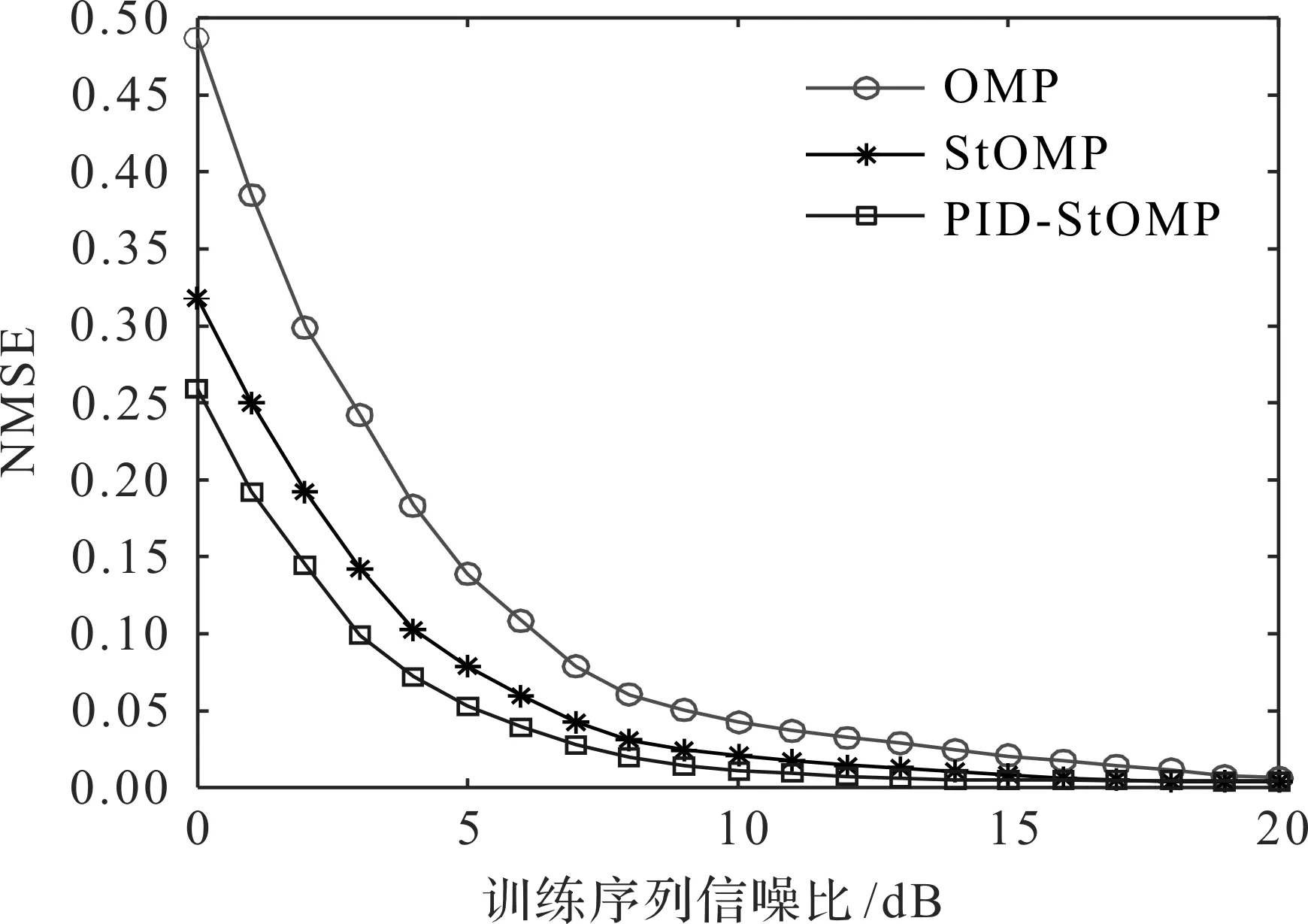
图5 小区用户数为8时，不同算法的性能

当单个小区用户数为8时，分别采用OMP算法、StOMP算法(其固定阈值为2.5)及PID-StOMP算法估计信道状态信息，得到3种算法的信道估计性能结果如图5所示。和图4相比，3种算法的估计误差均有所增大，因为随着小区用户数的增多，信道矩阵维度增大，导致计算复杂性增高，降低了估计精度。在0～5 dB低信噪比下，相比StOMP算法，PID-StOMP算法的训练序列信噪比性能提升了0.6～0.8 dB；相比OMP算法，PID-StOMP算法的训练序列信噪比性能提升更为明显。图3中，当小区用户数为8时，PID-StOMP算法的最佳原子挑选阈值为2.4，与StOMP算法固定的阈值2.5不一致，说明PID-StOMP算法能够根据当前的小区用户数寻找最佳阈值，从而降低了估计误差，体现了PID-StOMP算法的自适应优势。

结合图4和图5可以看出，在未知小区用户数即稀疏度不确定的情况下，本文提出的改进型自适应PID-StOMP算法依然可以根据当前无线信道状态搜索出最佳阈值，并用该小区用户数量相匹配的最佳阈值来换取信号重构精度的提升。

压缩感知贪婪算法的复杂度计算一般由3部分组成。PID-StOMP算法的复杂度计算如下。

(1)初始化部分：对当前残差进行匹配滤波即对矩阵AT进行操作，复杂度为O(MN)；用软阈值进行原子集合的获取和更新,复杂度最大为O(2N)；

(2)主循环部分：用共轭梯度求投影的最小二乘解，假设共轭迭代次数为v，与M，N不相关，为常量，复杂度为O(MNv)；

(3)输出部分：更新残差并计算当前残差能量是否符合迭代停止条件，复杂度为O(2MN)。

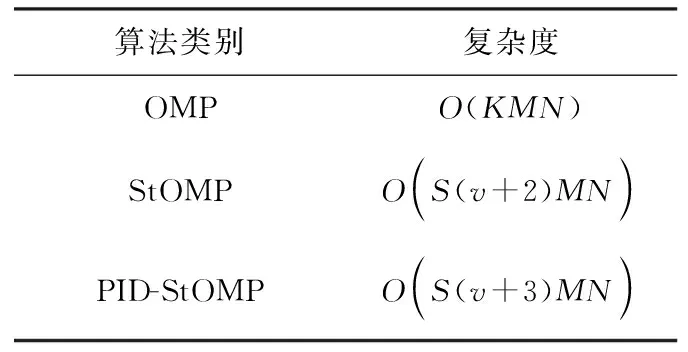
表2 不同算法复杂度对比

分别计算OMP算法、StOMP算法及PID-StOMP算法的复杂度，结果如表2所示。迭代时，StOMP算法和PID-StOMP算法可一次性挑选多个原子，而OMP算法在每次迭代时只可挑选1个原子，初始化时需要多次计算Cholesky因子分解，其复杂度更高。从表2可以看出，PID-StOMP算法和StOMP算法在极限条件下复杂度相近，但PID-StOMP算法凭借其自适应双阈值的特性可达到更高的重构精度。同时，相较于传统OMP算法，PID-StOMP算法更适用于大规模MIMO系统实际场景。

4 结束语

本文主要研究大规模MIMO系统，运用无线信道稀疏可压缩等特性，提出一种自适应双阈值的比例积分微分-分段正交匹配追踪算法，改善了低信噪比情况下信号重构精度较差的现象。下一步将构建虚拟角域信道模型，重点研究天线分组以及空间相关性对信道估计性能的影响，并根据具体场景下信道稀疏的表现，进一步优化算法的阈值选取方式。