交替方向乘子法解对称特征值互补问题

赵 寒，何洪津

(杭州电子科技大学理学院，浙江 杭州 310018)

0 引 言

特征值互补问题(Eigenvalue Complementarity Problem，ECP)是源于工程力学中的一类重要问题[1]。近年来，此类问题已被推广至张量形式，并称为张量特征值互补问题[2-3]。在特征值互补问题的内嵌矩阵为严格协正矩阵条件下，Júdice等[4]证明了特征值互补问题至少有一个解，且可等价转化为一个变分不等式问题。特别地，若相关矩阵为对称的，特征值互补问题还可转化为单纯形约束的瑞利商极大化问题。从转化后的等价形式上分析，瑞利商极大化问题为一般的约束优化模型，可采用谱投影梯度算法(Spectral Projected Gradient, SPG)[5]进行求解。目前，针对特征值互补问题提出的众多有效算法中，谱投影梯度算法是最受欢迎的方法之一，并被推广至求解张量特征值互补问题[6-7]。但是，谱投影梯度算法并未充分利用单纯形约束的特殊结构，每次需调用子程序来实现单纯形集合的投影。另外，谱投影梯度算法需调用线搜索寻找合适步长以保证目标函数值有一定的增长。对于大规模问题，线搜索无疑会增加计算成本。近年来，针对可分离结构优化问题设计的交替方向乘子法(Alternating Direction Method of Multipliers，ADMM)在大规模图像处理、机器和统计学习等领域取得了巨大成功[8]。为了提高特征值互补问题的求解效率，本文引入辅助变量，将单纯形约束进行分离，使得瑞利商优化模型变成可分的优化问题。在此基础上，采用交替方向乘子法对新模型进行求解，使其子问题都具有封闭解，达到有效规避单纯形约束的投影计算和线搜索循环过程的目的。

1 问题描述

特征值互补问题是指寻找1个实数μ>0和非零向量x∈Rn，使得

w=(μB-C)x，w≥0，x≥0，xTw=0

(1)

(2)

文献[10]的命题9指出优化模型(5)的稳定点即为对称特征值互补问题的解。此结论提供了一种求解对称特征值互补问题的有效途径。而且，文献[10]的命题10揭示：若C为严格协正矩阵(即对任意n维向量x≥0且x≠0，都有xTCx>0)时，对称特征值互补问题至少有1个解。本文假设对称特征值互补问题的解集非空。

2 交替方向乘子法

不难发现，瑞利商极大化模型(2)的单纯形约束可表示为2个简单凸集的交集形式，即,Δn={x∈Rn|eTx=1,x≥0}=X∩Y，其中

(3)

因此，通过引入辅助变量x=y，则问题(2)等价为：

(4)

上述问题是一类具有可分结构的简单约束优化模型。因此，本文采用交替方向乘子法对问题(4)进行求解。首先引入增广拉格朗日函数：

其中，λ∈Rn为拉格朗日乘子，β>0为等式约束的罚参数。给定第k步迭代点(yk,λk),交替方向乘子法的迭代格式为：

(5)

迭代格式(5)中的xk+1,yk+1子问题都是约束优化问题。但不难发现，xk+1子问题具有封闭解：

(6)

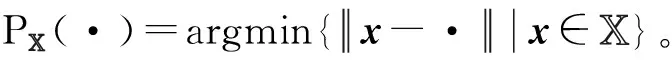
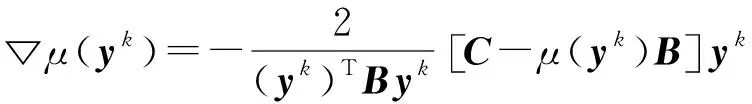
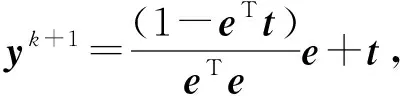
(7)

综上，可得求解对称特征值互补问题的交替方向乘子法，主要步骤如下。

初始化:给定初始迭代点(y0,λ0)∈YY×RRn,选择β>0和γ>0。(1)若迭代点满足某个停止准则,算法停止,否则转步骤2;(2)按式(6)更新xk+1;(3)按式(7)更新yk+1;(4)更新λk+1=λk-β(xk+1-yk+1)。

从本文算法不难发现，每一个子问题都具有封闭迭代形式。相比以往的算法，其迭代格式简单易实现。对于本文算法的停机准则，采用

来判断算法是否停止，然后再根据返回结果验证其是否为原问题的解。当然，也可根据优化问题的一阶最优性条件设计停机准则，如文献[5]中的停机准则。

由于优化模型(4)的目标函数为2个二次函数的商，根据文献[11]可知μ(y)为半代数函数，则μ(y)满足Kurdyka-Lojasiewicz不等式。又因单纯形约束集合为有界闭集，可知交替方向乘子法产生的迭代序列是有界的。因此，由文献[12]的推论3.1可知，{(xk,yk,λk)}收敛到模型(4)的KKT点，即原对称特征值互补问题的解点。因证明过程完全类似文献[12]的证明，本文省略算法的收敛性证明。

3 数值实验

本文通过2个算例来验证本文算法求解对称特征值互补问题的可行性。算法执行过程中，统一设定线性化参数γ=1。根据计算经验发现，交替方向乘子法取固定参数β时，对不同规模问题有一定影响。因此本文采用简单的调节准则调节算法，即每迭代10步，β值扩大0.2倍。所有试验运行环境为Windows 10操作系统下的MATLAB R2016a，配置为Intel Core i7-7700HQ CPU, 8GB内存的笔记本电脑。

算例1取B矩阵为单位矩阵，C矩阵为对称正定矩阵，满足C=MMT，

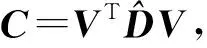
由文献[10]可知，算例1和算例2都至少有1个解，这保证了问题解集的非空性。特别地，根据文献[10]可知，算例1有唯一解，且解恰是C矩阵的最大特征值λmax(C)。

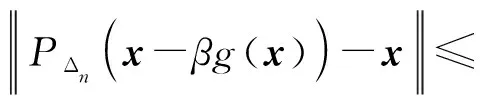
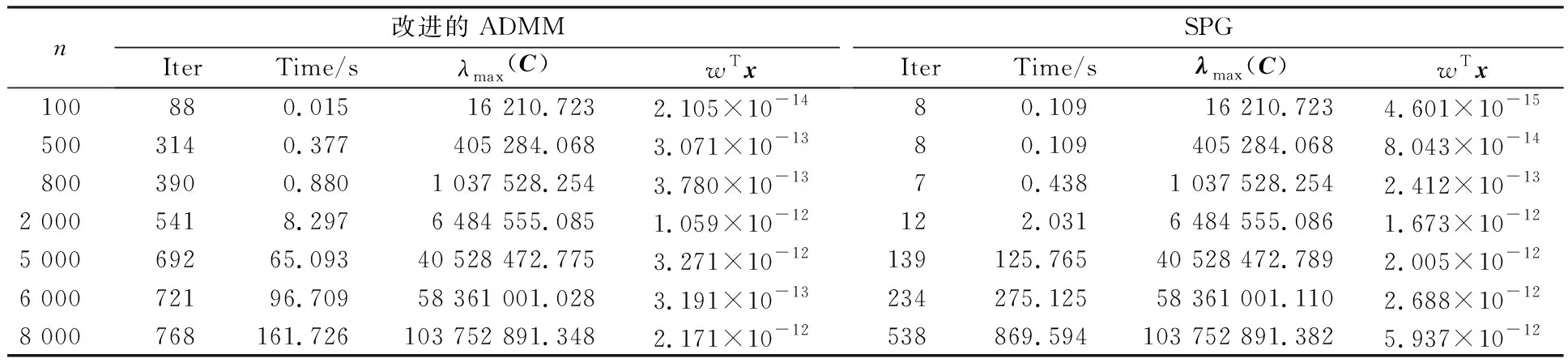
表1 2种算法求解算例1的数值结果

针对算例1，进一步讨论不同初始迭代点对交替方向乘子法的影响。本文选取2组初始迭代点y0=(1,…,1)，λ0=(0,…,0)和随机的y0=rand(n,1)，λ0=(0,…,0)进行分析，结果如表2所示。实验结果表明，初始迭代点的选择对本文算法影响较小，即使较大规模问题，本文算法依然能够在较短的计算时间内成功求解。

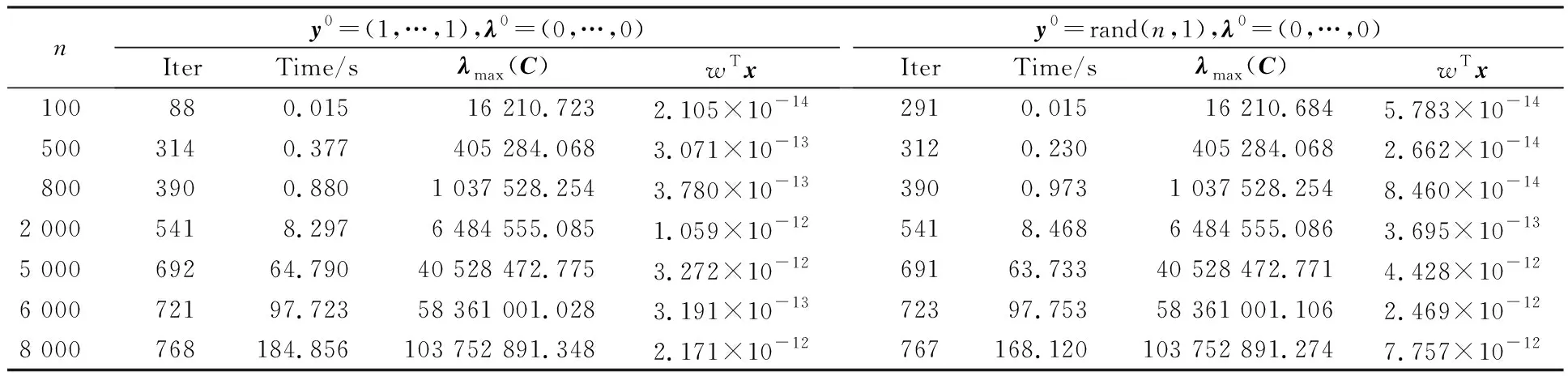
表2 不同初始迭代点对改进的交替方向乘子法求解算例1的影响

为了更进一步测试算法的收敛性，针对构造的算例2对每一个维度情况进行100次实验，并观察100次实验成功的次数Sn。表3列出了本文算法与SPG算法在停机精度取ε=10-6，罚参数β为103时的计算结果。实验结果表明，本文算法能在更短的时间内求解对称的特征值互补问题，其成功率可达100%。

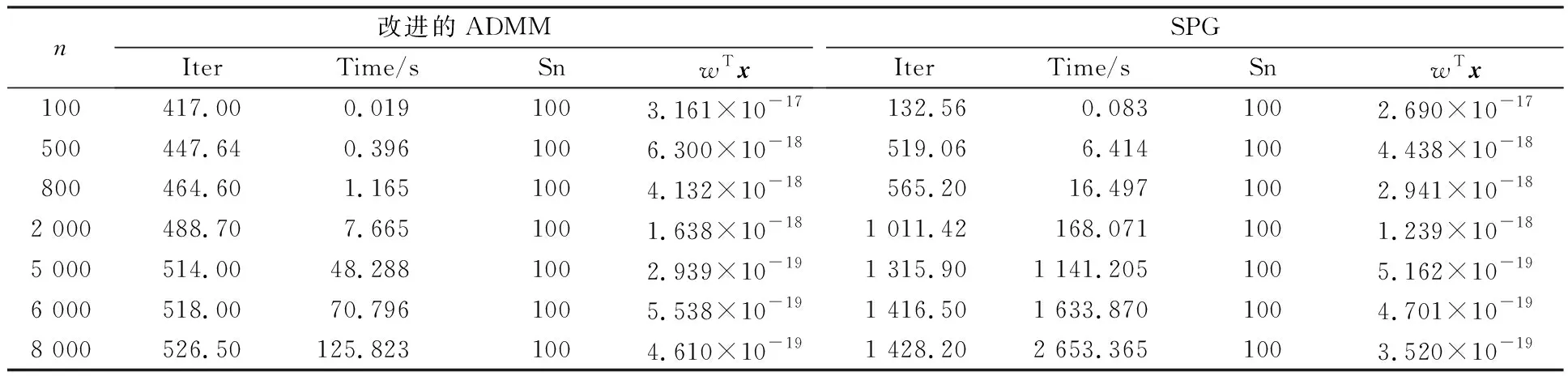
表3 2种算法求解算例2的数值结果

4 结束语

本文针对对称特征值互补问题提出了一种改进的交替方向乘子法。在计算较大规模问题时，改进算法用时较少，且初始迭代点的选取表现较稳定。但是，部分实际问题不一定满足本文的对称性要求，下一步将探讨非对称特征值互补问题的求解。