解锁 “隐圆”问题

卢会玉

(甘肃省嘉峪关市第一中学 735100)

在直线与圆的综合考查中，有时题设条件并没有直接给出相关圆的信息，而是隐含在题目中，要通过分析和转化，发现圆的方程或圆的定义，从而可以利用圆的知识来求解，这类问题常被称为“隐圆”问题.此类问题在高考中出现的频率比较高，通过对以往考题的分析与研究，可以总结为如下的几种题型.

一、利用圆的定义(到定点的距离等于定长的点的轨迹)可确定隐圆

题目中若已知到定点的距离等于定长或者能求出到定点的距离为定常数，则可以得到点的轨迹为圆.

例已知圆O：x2+y2=1，圆M：(x-a)2+(y-a+4)2=1.若圆M上存在点P，过点P作圆O的两条切线，切点为A，B，使得∠APB=60°，则实数a的取值范围为____．

解析由题意得,圆心M(a，a-4)在直线x-y-4=0上运动，则动圆M是圆心在直线x-y-4=0上，半径为1的圆.

又因为圆M上存在点P，使经过点P作圆O的两条切线，切点为A，B，使∠APB=60°，所以OP=2，即点P也在x2+y2=4上，记为圆E，则圆E与圆O一定由公共点.

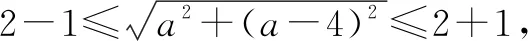
点评本题由∠APB=60°，得到OP=2，可推出点P在x2+y2=4上，即发现点P在一个圆上，于是顺利将问题转化为圆与圆的位置关系问题，进而轻松求解.

二、利用圆的性质(动点到两定点的夹角为直角)可确定隐圆

题目中若动点到两定点的夹角为直角，则可以得到点的轨迹为圆.

例在平面直角坐标系xOy中，直线l1：kx-y+2=0与直线l2：x+ky-2=0相交于点P，则当实数k变化时，点P到直线x-y-4=0的距离的最大值为____．

解法一直线l1，l2分别经过定点A(0,2)，B(2,0)，且l1⊥l2，所以点P在以AB为直径的圆C上．

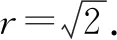
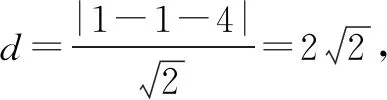
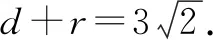
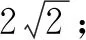
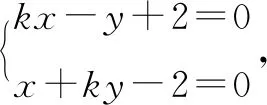
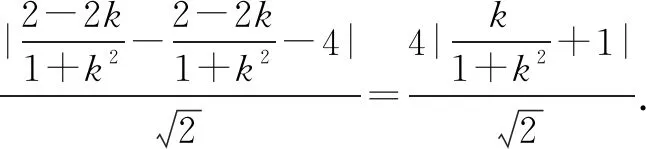
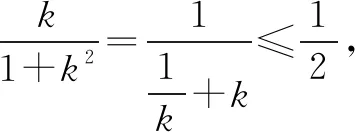
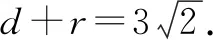
点评直接求出l1，l2的交点P的坐标(用k表示)虽然也能做，但计算量较大．找出点P变化的规律性比较好．本题的解法一明显好于解法二，可见发现“隐圆”的优势还是非常明显的.

三、已知两定点A，B，动点 P 满足为定值可确定隐圆

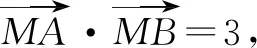
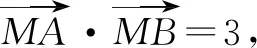
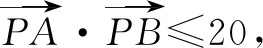
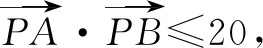
又因为x2+y2=50，所以2x-y+5≤0.

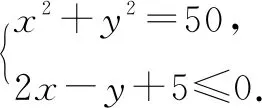
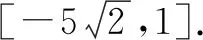
点评利用坐标法求点满足的方程是解决这类问题的常用方法．

四、已知两定点A，B，动点 P 满足PA2+PB2为定值可确定隐圆

已知两定点A，B，动点P满足PA2+PB2为定值的轨迹是圆.

例如图1，在平面直角坐标系xOy中，已知圆C：x2+y2-4x=0及点A(-1,0)，B(1,2)．在圆C上是否存在点P，使得PA2+PB2=12？若存在，求点P的个数，若不存在，说明理由.

图1

解析圆C的标准方程为(x-2)2+y2=4，所以圆心C(2,0)，半径为2.

假设圆C上存在点P，设P(x，y)，

则(x-2)2+y2=4，

又PA2+PB2=(x+1)2+(y-0)2+(x-1)2+(y-2)2=12，即x2+(y-1)2=4，是圆心为(0，1)，半径为2的圆.

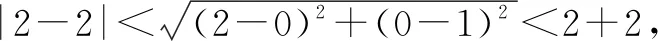
变式在平面直角坐标系xOy中，已知圆C：(x+1)2+y2=2，点A(2,0)，若圆C上存在点M，满足MA2+MO2≤10，则点M的纵坐标的取值范围是____．

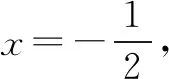
点评利用坐标法求点满足的方程也是解决这类问题的常用方法．

五、给定两定点A，B，动点P 满足AP=λBP(λ>0，λ≠1)的关系可确定隐圆

若给定两定点A，B，动点P满足AP=λBP(λ>0，λ≠1)的关系，则P点的轨迹为隐圆,我们称为阿波罗尼斯圆.

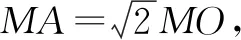
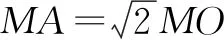
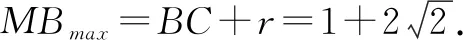
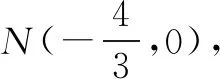
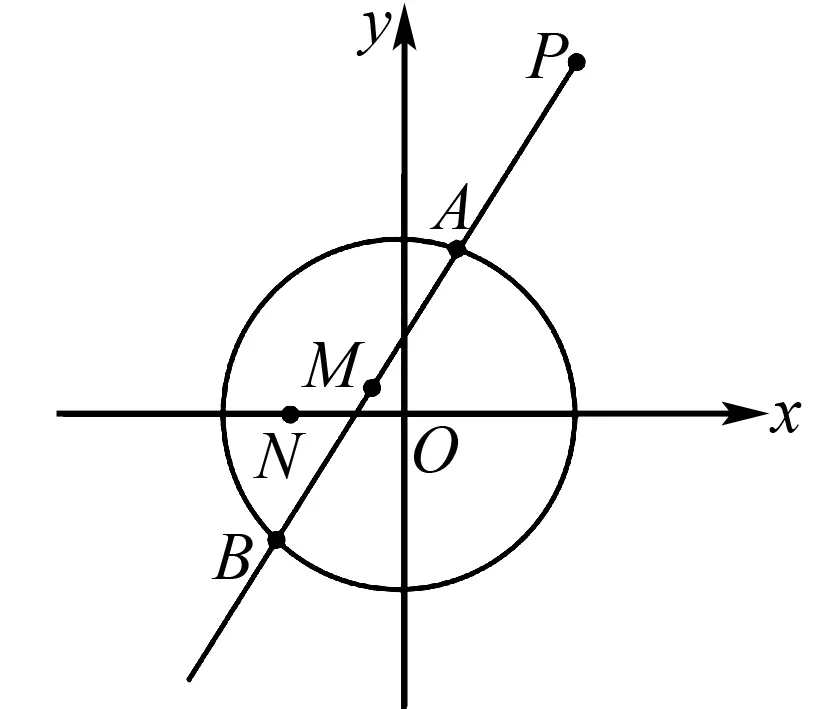
图2

解析设AB的中点M(x0，y0)，则OM⊥PM，所以

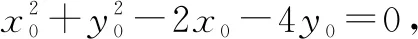
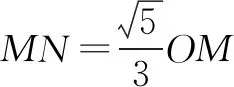
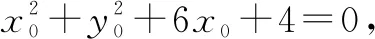
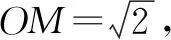
点评阿波罗尼斯圆是常见考点，能对学生分析和解决问题的能力进行深度考查，同时也应用了数学中的数形结合、归纳类比、转化化归等思想．

六、利用轨迹法确定圆

所谓轨迹法就是通过设点，根据题目中所给的条件得到轨迹方程．常见求轨迹的方法有：直接法、定义法、相关点法、参数法．

例在平面直角坐标系xOy中，已知点A(-1，0)，B(5，0)．若圆M：(x-4)2+(y-m)2=4上存在唯一点P，使得直线PA，PB在y轴上的截距之积为5，则实数m的值为____．

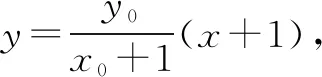
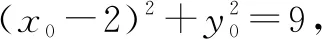
由题意P的轨迹应与圆M恰有一个适合题意的点，则：

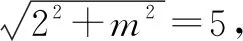
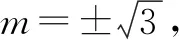
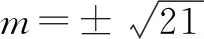
例在平面直角坐标系xOy中，已知B，C为圆x2+y2=4上两点，点A(1,1)，且AB⊥AC，则线段BC的长的取值范围为____．

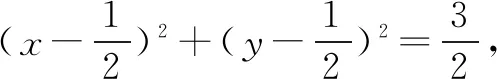
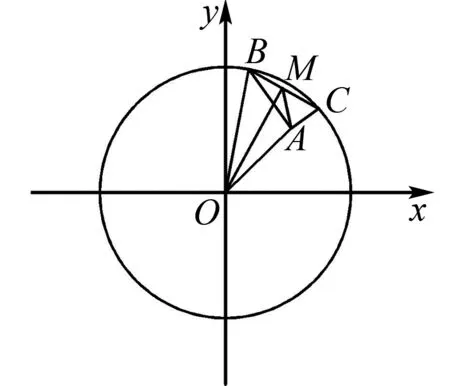
图3

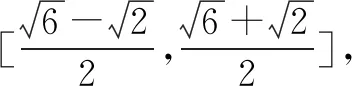
点评求轨迹问题要注意特殊点的判断.

“隐圆”问题的难点是通过对题目已知条件的分析，将问题合理的转化为圆，然后再利用圆的知识顺理成章的解决.解题过程中要注意充分利用圆的几何性质或一些简单的轨迹知识将问题转化为直线与圆或圆与圆的位置关系，进而求解范围等常见问题.