整体法在高中物理解题中的应用

刘家祥

(福建省上杭县第一中学 364200)

整体法是指在研究物理问题时，把所研究的对象作为一个整体来处理的方法.教学中为使学生能够灵活应用整体法解答相关的物理习题，应注重为学生讲解应用整体法解题的基本步骤以及应用时的注意事项，在分析物理问题时能够正确的选取研究对象，巧妙的破题.

一、用于解答受力分析习题

受力分析是高中物理的重要基础知识.为使学生掌握受力分析的技巧，提高受力分析效率，应引导学生运用整体法解答相关的习题，使学生体会到整体法在学习中的便利，提高在解题中的应用意识.

如图1，在大磅秤上放置一个大木箱，在箱内放置一个小磅秤.一人站在小磅秤上，某时刻其用力向上推木箱顶部，人和其他物体均处于静止状态，则两磅称的示数将( ).

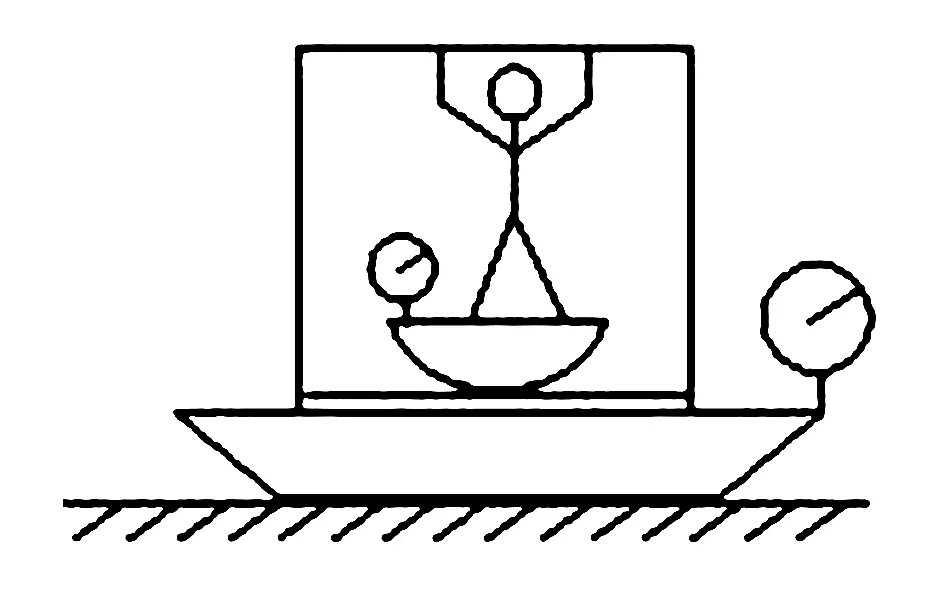
图1

A.小磅秤和大磅秤的示数都增大

B.小磅秤的示数增大，大磅秤的示数不变

C.小磅秤的示数增大，大磅秤的示数减小

D.小磅秤的示数不变，大磅秤的示数增大

题目考查了学生受力分析知识.分析时需要采用整体法与隔离法，正确处理整体与局部的关系.

分析大磅秤的示数时将人、小磅秤、木箱看做一个整体，人推木箱顶部属于内部的力可不考虑，因此，大磅秤的示数并不会发生变化.以人研究对象其向上推木箱，必然受到木箱的反作用力，促使其对小磅秤的压力的增加，因此，小磅秤的示数将变大.综上，正确答案为B项.

二、用于解答多次作用习题

物体多次作用相关的习题，过程较为复杂.如采取的方法不正确，不仅计算繁琐，而且容易出错.教学中为简化解题步骤，使学生少走弯路，可鼓励学生运用整体法进行分析，深化其对所学知识的理解的同时，更好的提高其解题水平.

如图2所示，在光滑的水平面上放置质量相等的5个物块，其间隔一定距离且排成一条直线.给予第1个物块初动能E0，使其依次与4个静止的物块发生碰撞，每次碰到后不再分开，最后5个物块连成一个整体，则这个整体的动能为( ).

图2

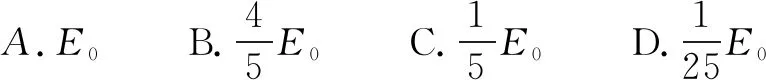
解答该题如逐一的考虑碰撞过程，需要多次使用动量守恒定律，较为繁琐.而使用整体法，将5个物块看作一个整体，只需要经过简单的计算，便可得出正确答案，解题效率明显提升.

将5个物块看作一个整体，设每个木块的质量为m，起初第1个物块的速度为v0

由动量守恒定律得：mv0=5mv，

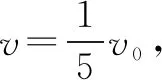
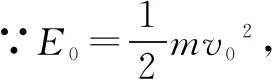
选择C项.

三、用于解答简谐运动习题

简谐运动是物体运动的常见形式，是高中物理的重要知识点.解答简谐运动相关习题应认识到整体法的重要性，根据题设情境灵活运用整体法以及隔离法，构建对应的方程求解出相关的参数.

如图3所示，一弹簧振子的质量为M，他的劲度系数为k.某时刻在振子上放一质量为m的木块，使其一起在光滑水平面上运动.木块的回复力F也满足F=-k′x，x为离开平衡位置的位移，则k′/k=( ).

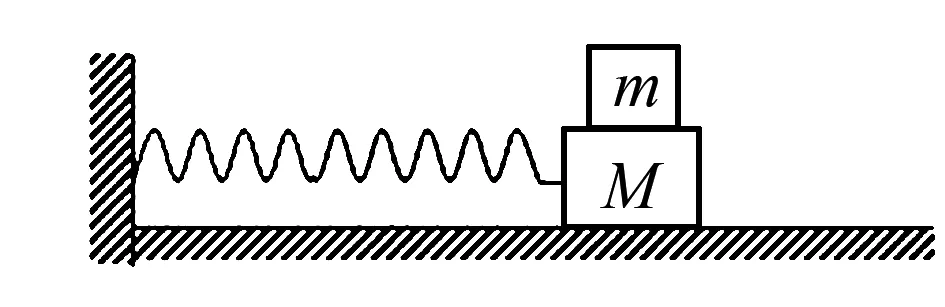
图3

解答该题既需要从整体上进行考虑列出对应的方程，又需要将m隔离开来进行单独分析，列出方程，才能求得k′/k的比值.

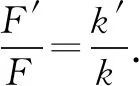
四、用于解答综合习题

高中物理综合类的习题对学生思维灵活性、解题技巧有一定要求，因此应注重为学生展示相关例题，并注重讲解整体法在解答综合习题中的应用，为学生以后更好的解题带来良好启发.

如图4所示，在光滑的水平面上放置A、B、C三个滑块，对应的质量依次为2m、m、3m.其中A、B之间压缩一弹簧并使用与轻绳连接(弹簧和滑块不栓接).开始时A、B以相同的初速度v0向右运动，C静止.某时刻轻绳突然断裂，A、B被弹开，而后B和C发生碰撞并粘在一起，最终三滑块速度恰好相同.求整个过程中弹簧释放的弹性势能和系统损失的机械能之比.

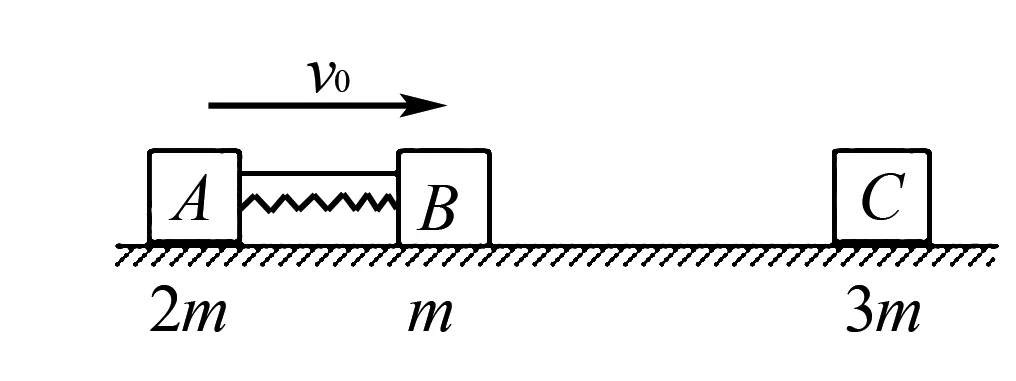
图4

解答问题需要从整体上进行考虑.其中弹簧释放的弹性势能等于A、B动能的增加量.而系统损失的机械能主要由B和C的碰撞引起，因此，求解弹簧弹开后A、B滑块的速度以及B和C碰撞后的速度成为解题的关键.

以A、B为一个系统，弹簧弹开前后的动量守恒.设向右为正方向，弹簧弹开后A、B的速度分别为vA、vB.

由动量守恒定律可知：(2m+m)v0=2mvA+mvB.

将B、C看做一个系统，碰撞后的共同速度为vC

由动量守恒得到：mvB=(m+3m)vC，又∵vA=vC.

设弹簧的释放的弹性势能为Ep，以A、B为研究对象，由机械能守恒得到：

设BC碰撞后损失的机械能为ΔE损，则碰撞前后由能量守恒得到：

以上各式联立得到Ep/ΔE损=1∶2.

整体法是一种重要的学习方法，为提高学生应用整体法解题的意识与能力，既要注重相关例题的讲解，又要组织学生开展专题训练活动，使学生不断的积累相关的应用经验与技巧，遇到相关习题能够迅速的找到解题思路，实现高效、正确解题.