试论高中数学函数题多元化解题思路

范鹏春 刘凤娣

(福建省上杭县第一中学 364200)

一、多元化解题思路

我国著名的教育学家陶行知曾明确指出，教育理念为生活与教育，不管任何一个学科，知识均来源生活当中，其价值又高于生活，数学学科也是如此.数学知识与日常生活之间有着密切的联系，在数学知识解题阶段，函数学习能够锻炼自身的问题解决能力，能够培养自身的逻辑与思维，可促使自身学习效率得到提升.在高中数学函数知识解题期间，教师要借助多元化的解题思维，增加自身全面发展的几率.

二、高中数学函数题多元化解题思路

高中数学知识比较复杂，且涉及较多的概念，课堂解题枯燥且呆板，为将课堂有效性、趣味性提升，必须要注重自身数学思维能力的培养，促使自身树立终身学习理念.各大高校要积极改革，不断强化，将原本传统的解题方式转变，注重解题内容、手段及形式的创新.

1.强化发散性思维的应用

促使自身综合运用不同的知识，能够使用多种方式将问题解答.自身自己观察，能够发现并总结问题，掌握解题规律，实现自身问题分析与解决能力的提升，激发自身的发散性与创造性思维.笔者结合多年经验认为，自身发散思维的培养，可以一题多变，扩展思维空间，培养自身的创造性思维.将原本枯燥的数学氛围变得活跃，促使自身参加一题多解、一题多变的解题活动，在学习中获得成就感，就数学学科产生浓厚的兴趣.

例1设二次函数f(x)=ax2+bx+c(a>0),解方程f(x)-x=0.由方程与二次函数的学习可知，在二次函数解题中，会伴随解方程，以解方程的方式解答二次函数问题.因此，在开展多元化解题思路中，本题我们完全可以利用方程解题.

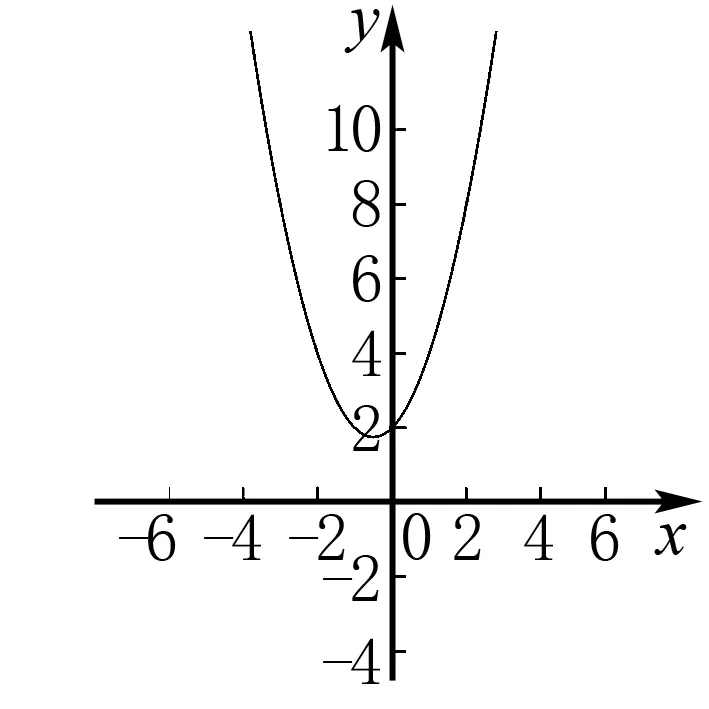
图1

由已经条件f(x)-x=0，f(x)=ax2+bx+c(a>0)可以得出ax2+bx+c=0(a>0)，ax2+bx+c=0(a>0)是典型的一元二次方程.由一元二次方程中根与系数的关系的对方程ax2+bx+c=0(a>0)进行解方程，进而得到函数字母字数abc所代表的真实数字，达到解题目的.多元化的解题思路，顾名思义，是从多角度进行解题.那么在本题中，就要求教师在熟练掌握二次函数以及方程相关知识的基础上，形成知识体系，以便于教学中， 有的放矢，将多元解题思路高质量融合教学中.同样以本题为例，从图象解题思路分析，f(x)-x=0是直线y=x表达式，f(x)=ax2+bx+c(a>0)代表着抛物线.那么，由抛物线与直线相交，我们便可以得到第二条解题思路.除此之外，在进行本题分析时，我们不难发现不等式推导与求根公式的结合同样是本题解题思路之一.

2.触类旁通

在数学知识学习过程中，“苦思冥想”固然重要，但也要注意“巧思”两字不可少.“熟能生巧”，自身想要对所学知识的融会贯通，必须要借助巧思.教师要顺应时机，为自身介绍典型的实例，促使自身掌握解题的方式，掌握解题的技巧.针对性的汇编相应的习题，促使自身在实践中去找寻变通点，掌握其来龙去脉.掌握科学的解题法则.那么，“触类旁通”的“巧妙构思”也一定会自然而流畅的产生，使自身思维在不断地展开中得到充分的训练和培养.同样以例：二次函数f(x)=ax2+bx+c(a>0)，解方程f(x)-x=0为题.在进行本题解答时，从多元化解题思路培养与实践出发，我们找到了三种解题方法，分别为图象解题法，方程中根与系数的关系解题法以及巧妙利用不等式推导，将不等式推导与一元二次方程结合的方法解答二次函数f(x)=ax2+bx+c(a>0)问题.

由以上可知，在本题解题中，我们分别利用了不等式推导，一元二次方程等知识点.就二次函数f(x)=ax2+bx+c(a>0)而言，二次函数f(x)=ax2+bx+c(a>0)是一个独立知识点，即二次函数.但进行多思路解题时，我们用到了不等式推导与一元二次方程，这便是触类旁通的巧妙用法.

由二次函数f(x)=ax2+bx+c(a>0)引出一元二次方程ax2+bx+c=0(a>0)，由二次函数f(x)=ax2+bx+c中(a>0)开口向上，进一步引出不等式，进行二次函数解题.

3.掌握数形结合解题思想

在高中数学学习中，数形结合是我们常用的数学解题思想.其多以图象的直观表象与数量的精准表达给予我们启发.

例如:选择题，如果f(x)=x2+bx+c对于任意一个实数t都必须具有f(2+t)=f(2-t),那么以下选项哪个正确？

(1)f(1)

(2)f(2)

(3)f(2)

(4)f(4)

由已知条件f(x)=x2+bx+c对于任意一个实数t都必须具有f(2+t)=f(2-t)可知，在进行本题解答时，若以代数方法解答会存在较大困难，但经过分析，f(2+t)=f(2-t)的图形特征(如图2)，能够很容易通过单调性得出结论，即f(2)

图2

4.有效提问

为了激活自身函数学习的兴趣,弱化自身的函数学习压力,让自身能够循序渐进的感知函数知识、理解函数知识.高中数学教师在开展函数解题时就要适当创新解题方法,引自身参与到函数学习的空间内,丰富自身函数学习的趣味体验.情境创设法是高中数学教师开展函数解题的重要方法,它能够通过趣味情境的创设让自身参与到函数学习之中,舒缓自身函数学习紧张情绪,同时引导自身积极思考函数相关知识.

如：设f(a+1)=a2-4a+1,求f(a).在进行本题解答时，首先，常规表达式中定义域中元素通常由x表示，或x表达部分未知数，但本题中定义域元素由a表示.这时，我们可以暂且忽略a与x的字母差异.一般情况下，本题有两种解答方法.

(1)变量代换法.应用变量代换法时，我们可以将a+1用字母T表示，即T=a+1，得出a=T-1，再将含有T-1的式子带入，得出f(a)=a2-6a+6.

(2)整体法.将a+1看作整体，将a2-4a+1表示成a+1的多项式，即f(a+1)=(a+1)2-6(a+1)+6,得出f(a)=a2-6a+6.

总之，函数，是数学思想也是数学灵魂，是高考的考查重点.高中数学教师应当尽可能地在解题实践中积累解题经验，既要关注自身函数学习的学习体验，又要逐步培养自身函数的应用意识.只有这样函数解题的解题效率才会有效提升，解题目的才能够顺利达到.