物理特色“构造法”在问题解决中的应用

何乐晓

(浙江省杭州外国语学校 310023)

所谓构造法，就是在解题时，通过对条件和结论的分析，构造辅助元素，架起一座连接条件和结论的桥梁，从而使问题得以解决.构造法是数学解题中的一种重要而基本的方法，在以数学为工具的物理问题解决中也常有妙用.

物理特色的构造法，就是根据题设条件或结论所具有的特征、性质，构造出合适的物理情境或过程，并借此解决物理问题的方法.

构造法是一种富有创造性的解题方法，是培养学生创造性思维能力的一种有效途径.

一、构造物理过程

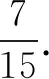
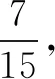
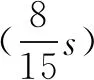
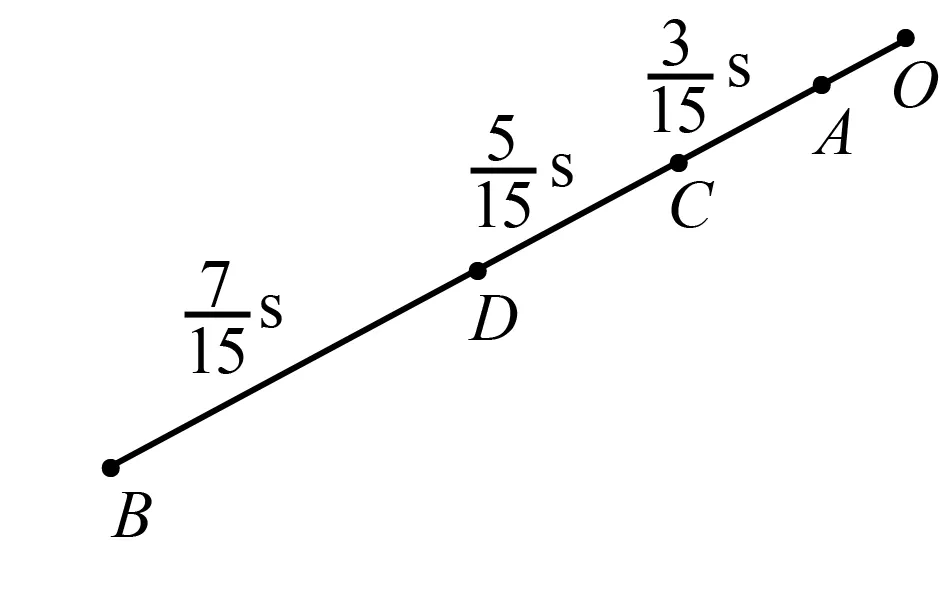
图1

故由A到B所用时间t=3t0=3s

斜面长度s=(3+5+7)sOA=15m

二、构造全新情景

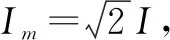
解析可以考虑构造这样的全新情景：把如图2所示的正弦交流电和余弦交流电，分别同时通入阻值均为R的两个电阻，则这个系统在任意时刻的热功率为：

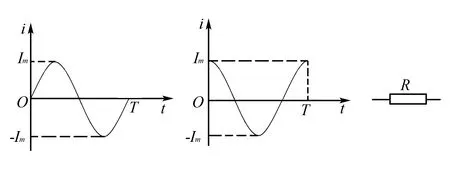
图2

此系统在一个周期内产生的热量为

显然，这两个交流电在一个周期内产生的热量相等，再设它们的有效值均为I，那么在一个周期内该系统产生的热量和为Q2=2I2RT

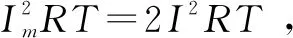
三、构造组合模型

问题3两个等量异号的点电荷，当它们之间分开的距离比讨论中所涉及的距离(例如所考察的场点到它们之间的距离)小得多时，这一对点电荷称为电偶极子.下列三小题中，真空中带电量为+q和-q的电偶极子间距为l，各点到两电荷连线中点距离为r，r远大于l.

(1)如图3，p为两电荷连线延长线上一点，求p点处的场强大小；

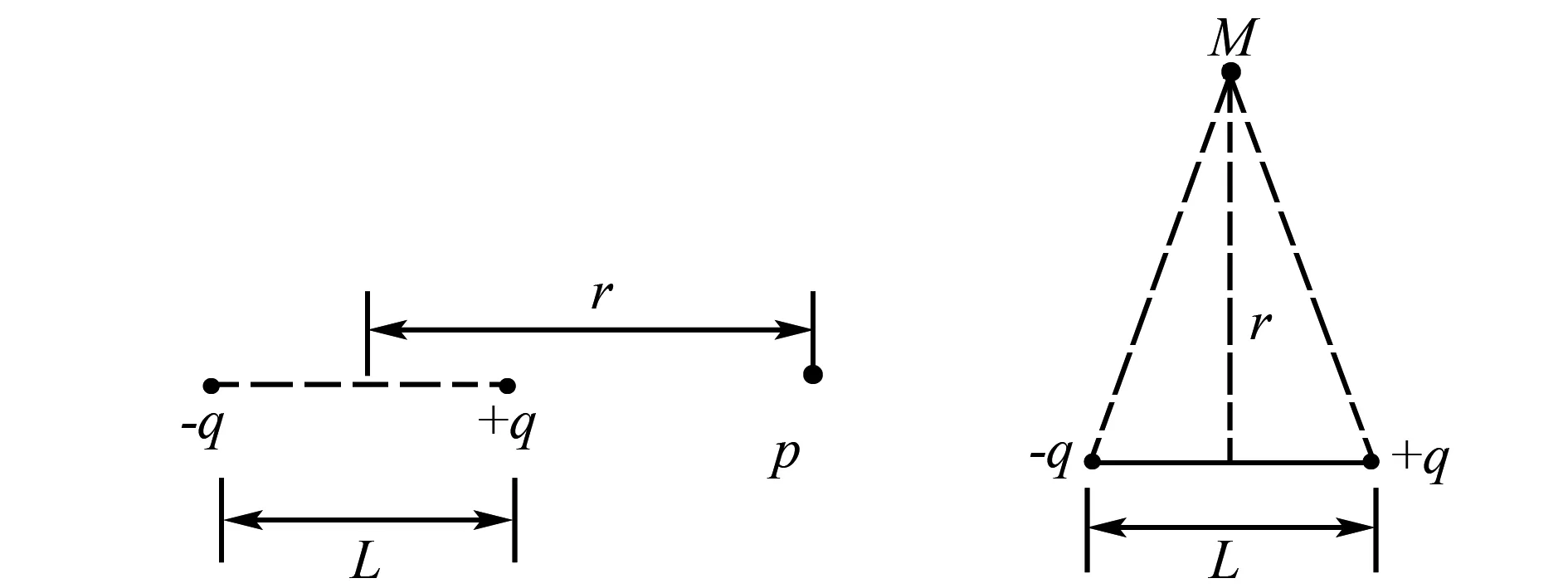
图3 图4

(2)如图4，M点为电偶极子中轴线上一点，求M点处的场强大小；

(3)如图5，T为空间任意一点，T与中点连线和两电荷连线的夹角为θ，求T点处的场强大小.

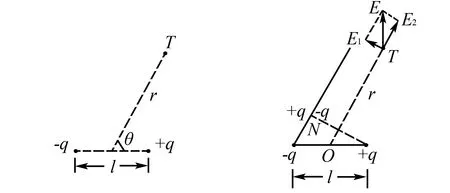
图5 图6

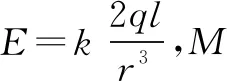
下面重点分析第(3)小题.这个小题的难度不小，可以考虑：能否把这一小题要求的普遍情况转化为前两种特殊情况来解决？

如图6所示，过+q所在的点作OT的垂线，过-q所在的点作OT的平行线，交于N点，N点不带电，但可设想其电量为+q加-q，则它们与原来的电偶极子构成了两对电偶极子.由于电偶极子间的距离l远小于T与两电荷连线的中点的距离r，所以，T可视为是一对电偶极子两电荷连线延长线上一点，同时T也是另一对电偶极子两电荷连线中垂面上一点，这样，通过构造，把一对电偶极子变成了等效的两对电偶极子，顺利地把要求的普遍情况转化为两种特殊模型的组合.

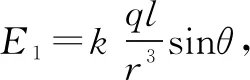
四、构造公式

必修二“万有引力定律”一章的第二节内容，是研究太阳与行星之间的引力，在推导太阳对行星的引力公式时，构造法起到了重要作用.

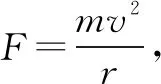
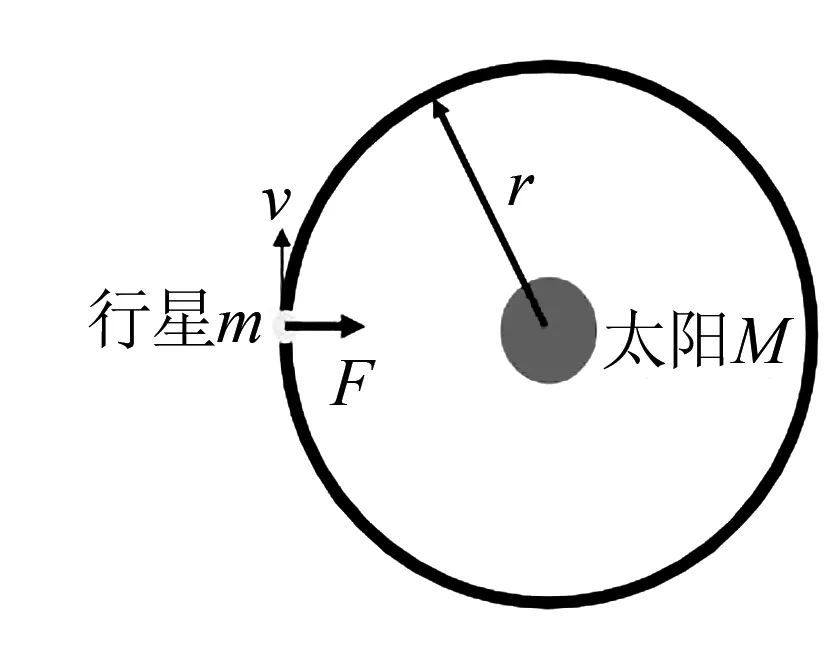
图7

考虑到此前，与此相关的天体运动的量化规律只有开普勒第三定律，可据此设法构造.

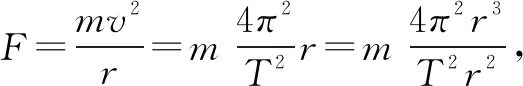
从以上几个问题的解决可以看出，物理特色的构造法是一种创造性、技巧性很强的思维方法，若对一些难题、繁题使用得当，常会有简洁明快、四两拨千斤的神奇效果.