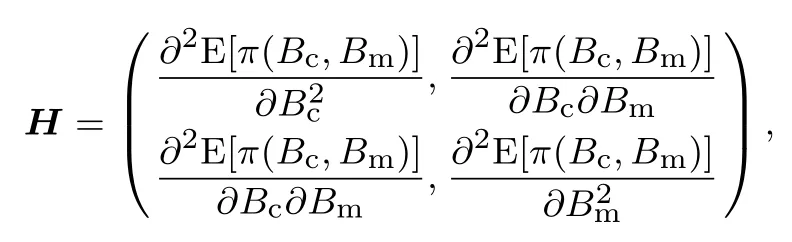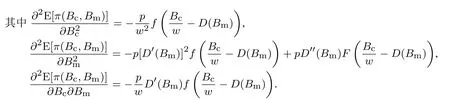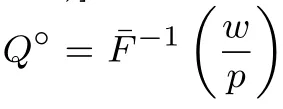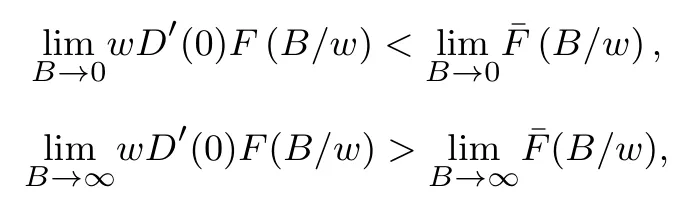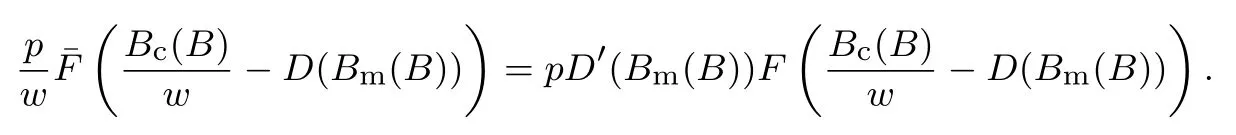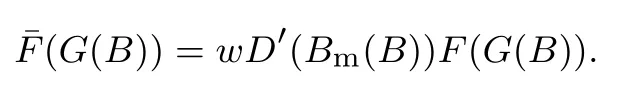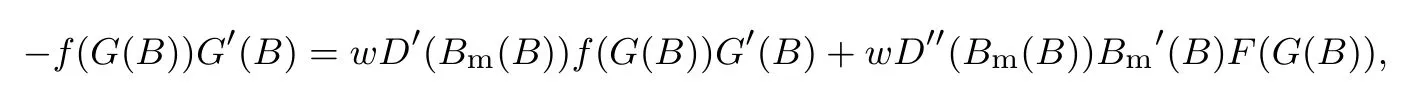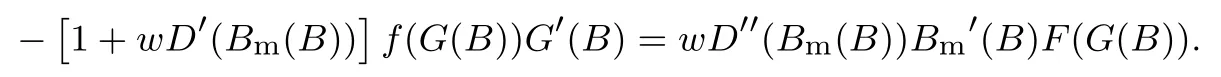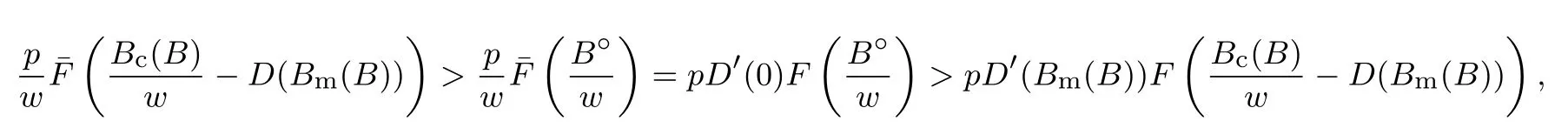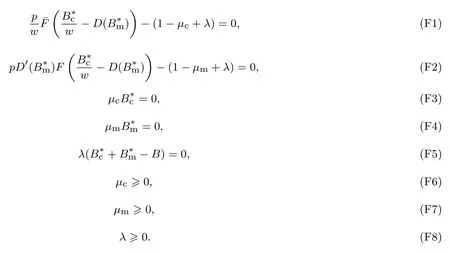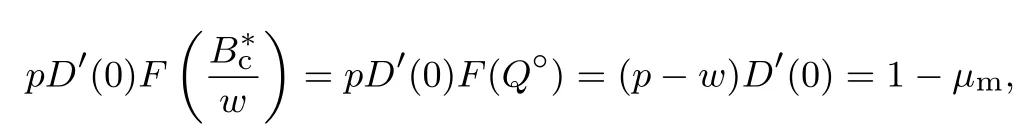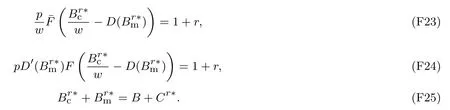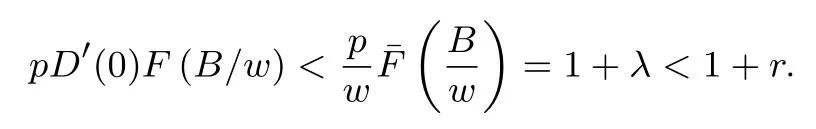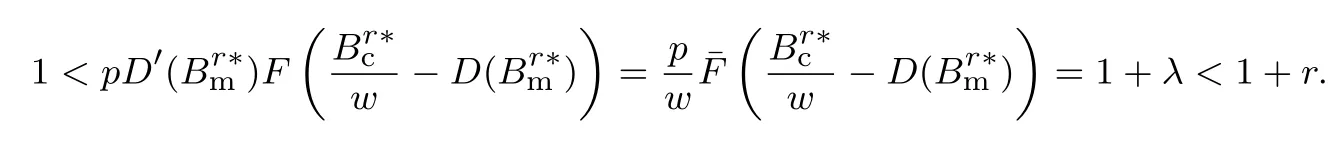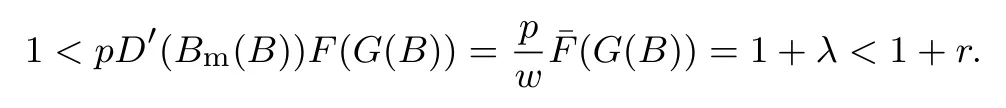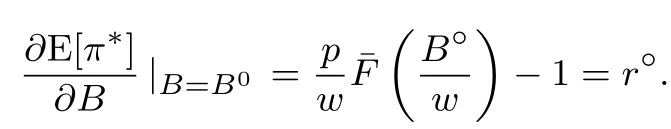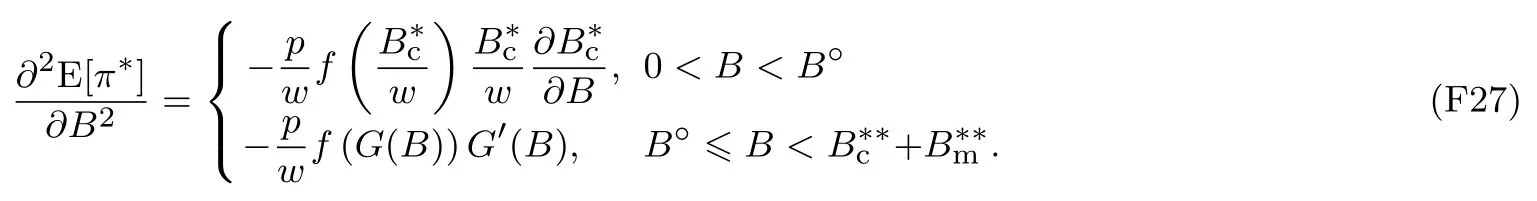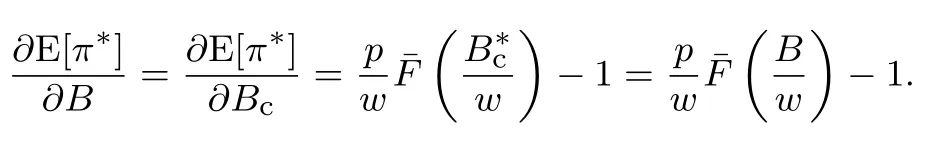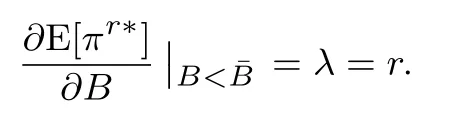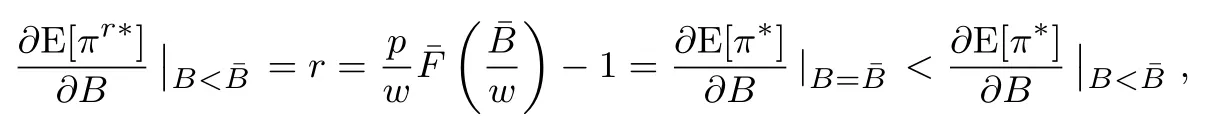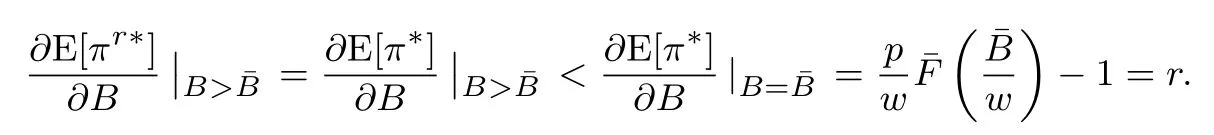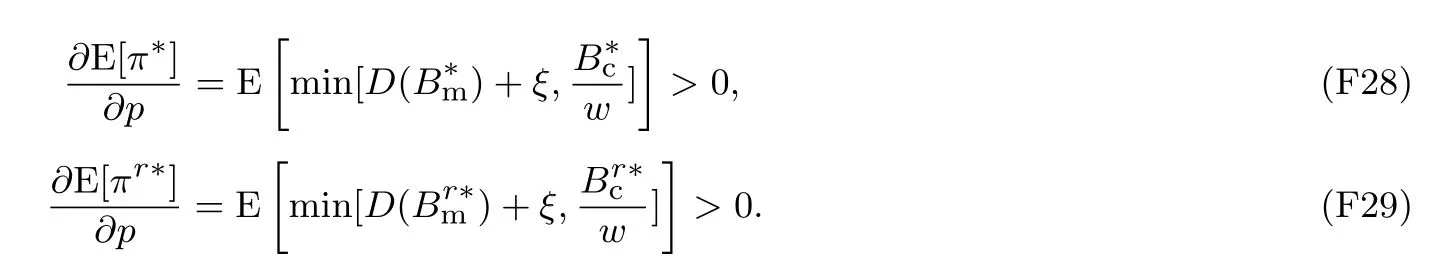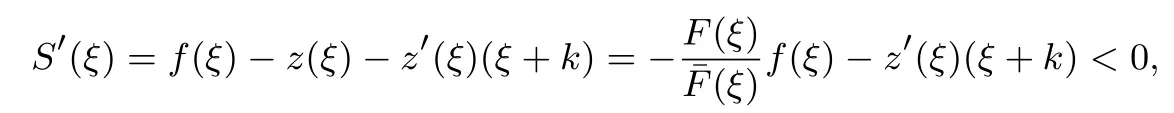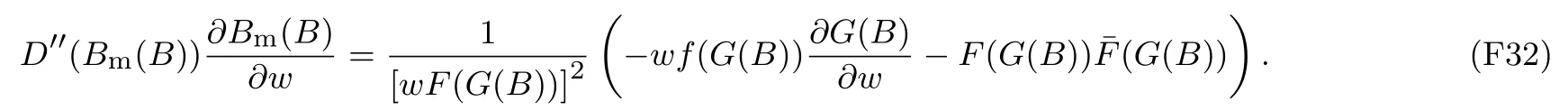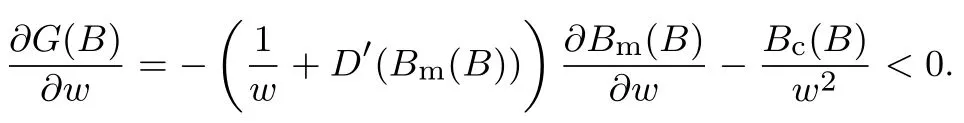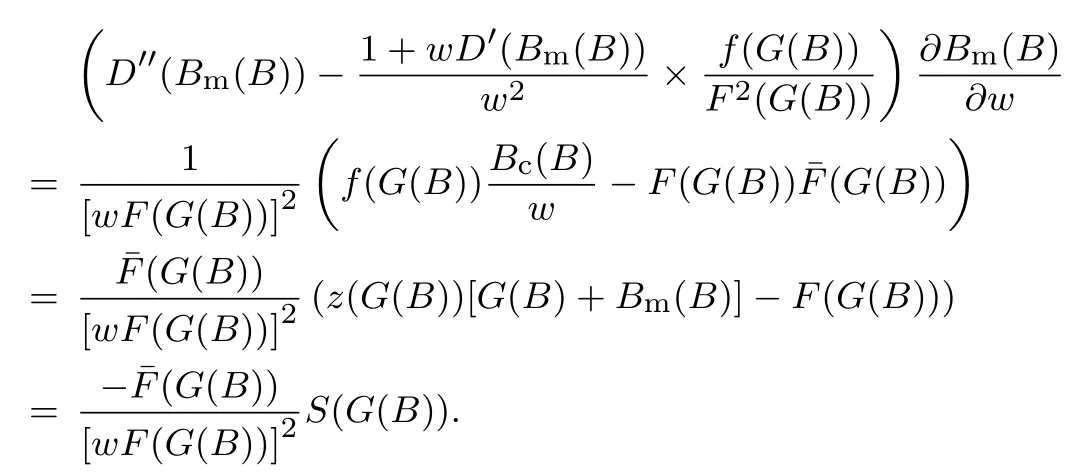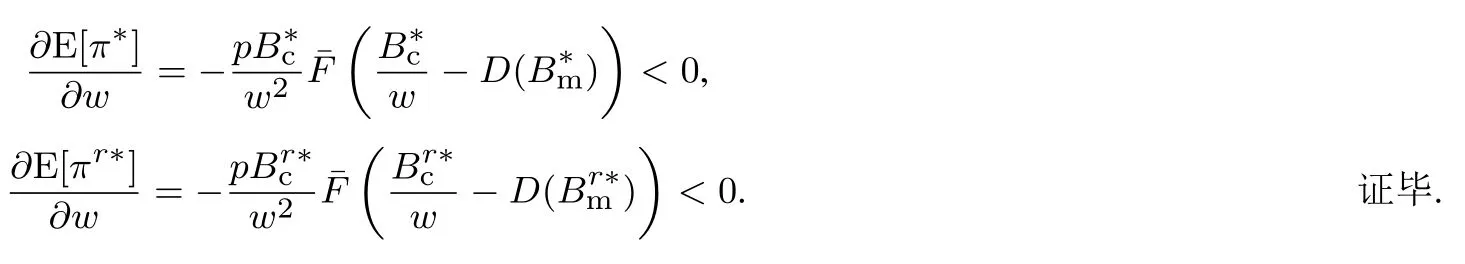资金约束零售商订购、促销与融资协同决策分析
代建生, 牛清洁
(1.昆明理工大学管理与经济学院,云南昆明650093;2.重庆大学经济与工商管理学院,重庆400030)
1 引 言
在创业初期或快速发展时期,很多企业面临运营资金不足的问题[1],这在业务比较单一的中小企业中表现得尤为明显.资金短缺制约企业的日常经营,阻碍企业的业务发展,严重的资金短缺可能导致企业破产[2], 因资金链断裂而破产的著名企业包括荷兰跑车制造商世爵及青岛海尔丰彩印刷公司.在金融危机后,越来越多的企业日益意识到现金流管理的重要性,希望通过降低库存水平和资金周转周期等方式来保证现金流的安全,“现金之战”使得中小企业的资金约束问题更加突出和严峻.由于资金短缺企业难以实现与市场需求相匹配的生产或订货规模[3,4],因而融资服务在现代企业管理中起到非常重要的作用.如果资金短缺企业能够通过金融市场获得财务资源,并实现融资与运营的相互协同,则能显著地改善运营绩效.
随着市场竞争的加剧和需求不确定性的增加,零售企业面临越来越高的市场风险,尤其是运营资金短缺的零售企业,它们不仅需要采取促销手段来获取竞争优势,还必须优化其订购决策以减少经营风险.零售商的订购和促销策略交互影响,如果商品采购数量较大,则须加大促销力度以减少出现剩余商品的风险;如果零售商计划实施更为激进的促销方式,则应在销售期前加大商品的采购数量.零售商无论是采购商品,还是开展促销活动,都需要运营资金支持,因此,零售商的订购和促销决策必然受制于可支配的运营资金.在资金短缺下,是否开展促销活动?商品采购和促销活动两者之间的资金如何配置?是否需要对外融资?融资多少?等等,是零售商需要统筹协调的重大决策问题.
上述问题在理论上可抽象为融资、订购和促销的协同决策问题,虽然已有不少文献探讨了融资与运营的协同决策问题,但鲜有文献讨论融资、订购和促销的联合决策问题.本文对此问题进行了研究,并在不融资和外部融资两种情形下分别刻画零售商的运营策略,揭示了零售商的融资、订购和促销策略以及收益关于初始资金、金融市场利率、销售价格和采购价格的变化规律.
本文的研究与订购决策问题尤其是需求随机下的报童问题紧密相关.传统的订购决策问题在资金充足假设下进行讨论,有关研究进展可参考Qin 等[5],其中涉及到订购与促销联合优化问题的有文献[6–8].代建生[9]在供应链背景下探讨了零售商的订购和促销协同决策问题.张菊亮[10]研究了多周期联合促销与库存控制问题,在每一周期,决策者同时确定促销水平和订货量,他们刻画了决策者的最优促销和订购策略.本文将在资金约束下探讨融资、订购和促销的协同决策问题,这不同于上述研究.
本文可归属为资金约束下的报童问题的文献.相关研究可分为两类, 其中一类不考虑融资问题而致力于探讨资金短缺下的订购决策问题[11,12],而另一类文献则在资金约束下考察融资与运营的协同决策问题,Buzacott 等[13]对资金约束和无资金约束下的最优订货决策进行了比较分析.陈祥锋等[14]研究了外部融资下零售商的融资和库存综合决策问题,并分析了融资服务对运营绩效的影响;在此之上,陈祥峰[15]探讨了承担有限责任的零售商在贸易信用合同下的采购策略.Kouvelis 等[16]考察了存在破产成本下零售商的融资和库存决策,并分析了破产成本对供应商定价决策的影响.Kouvelis 等[17]在贸易融资下探讨了零售商的融资和库存决策,并在此基础上刻画供应商的最优合约结构.王文利[18]在两阶段随机需求环境下,给定供应商向资金约束零售商提供的交易信用融资,分析了零售商的最优订货策略,并与无资金约束情形进行了比较分析.最近,Chod[19]研究了融资对库存决策的扭曲效应,并对银行信用和贸易信用下库存决策进行了比较分析.史金召等[20]在提前订购和延时采购两种情景下,分别考虑最大化期望收益和最小化违约概率两种决策目标,分析了零售商的最优采购和融资策略.上述研究虽然探讨了融资与运营(商品订购)的协同决策问题,但没有分析资金约束企业的初始资金、市场利率等因素对融资与运营决策的影响.本文完整地刻画了在不同初始资金和市场利率下零售商的融资、订购和促销策略,分析了初始资金、市场利率、销售价格和采购价格等因素对零售商决策和收益的影响,得到一系列新的研究结论:无论是否存在融资机会,零售商的初始资金越大,其实现的收益越大,且初始资金对收益的影响程度随初始资金的上升而递减;市场利率升高,零售商将减少贷款,使用更少的资金用于商品采购和促销活动,实现的收益降低,且利率对收益的负面影响随着利率的上升而递减.
窦亚芹等[21]研究了金融市场的竞争程度、初始资金量和破产成本率对零售商库存策略的影响.张小娟等[22]在零售商可以仓单融资后进行二次订购的背景下,刻画了零售商在不同的初始资金量下最优仓单抵押率及最优订购策略.李荣等[23]在风险厌恶下分析了资金约束零售商的订购策略,并考察了风险态度和初始资金对订购决策的影响问题.上述研究都讨论了初始资金对订购决策的影响,但与本文存在以下不同,第一,本文分析了初始资金对订购和促销决策的联合影响,结果表明,用于商品采购和促销活动的资金实现的边际收益相互依赖,因此,零售商必须合理配置商品采购和促销资金.第二,对比分析了不融资和外部融资两种情形下初始资金对零售商决策和收益的影响差异,结果表明,外部融资下初始资金对零售商决策和收益的影响小于不融资的对应情形.
杜文意等[24]的研究与本文最为相近,他们在外部融资下探讨了零售商的库存与促销协同决策问题,分析了零售商持有的初始资金对库存和促销决策的影响.本文与杜文意等[24]的研究至少有以下三点不同,首先,杜文意等[24]关注的重心是零售商的运营与银行的利率定价的交互影响,通过构建关于银行和零售商的斯塔伯格博弈模型,其中银行居于主导地位,他们刻画了银行的最优利率以及零售商的最优订购和促销策略;与之不同,本文在金融市场充分竞争假设下进行讨论,力图刻画零售商在不同贷款利率下的融资、订购和促销策略.其次,杜文意等[24]没有刻画零售商促销的临界条件,而是隐含地假定零售商一定会实施促销努力,但本文的研究表明,只有当零售商的初始资金和贷款利率满足一定条件下,零售商才会促销,当这一条件不被满足时,零售商将把所有可用资金(包括初始资金和银行贷款)用于商品采购.最后,杜文意等[24]在零售商实施贷款下进行讨论,没有刻画零售商融资的临界条件,是本文研究的一个特例;本文的研究表明,如果初始资金足够高以至于资金运用的边际收益低于融资成本,零售商将不对外融资.
本文揭示了零售商的融资、订购、促销策略以及收益关于初始资金、金融市场利率、销售价格和采购价格的变化规律.刻画了零售商融资和促销的临界条件,分别回答了零售商应在什么情形下融资以及促销的问题.得到了一系列新的研究结论,当市场利率较低时,相对于不融资的情形,在外部融资下零售商将花费更多的资金用于促销,且市场利率越低,零售商的促销力度越大;在资金短缺下,随着采购价格的上升,零售商将增大对商品采购资金的运用,同时减少促销资金的运用.最后,本文的研究也为解释与促销有关的部分经济现象提供了新的理论视角.
2 零售商促销下的资金约束模型
考虑经营单一商品的零售商, 在不促销下商品潜在市场需求量记为ξ, 它是一个随机变量, 其分布函数和密度函数分别为F(·)和f(·), 为了讨论方便, 约定f(ξ) > 0, 并记(ξ) = 1 −F(ξ).零售商的采购价格为w, 销售价格为p.零售商经营报童类商品, 需在销售期前确定订货量Q, 其用于商品采购的资金Bc= wQ.在不考虑促销和资金约束下, 零售商面临的问题是经典的报童问题, 其最优订购量为Q°= F−1(w/p).
在不调整销售价格下,零售商开展促销活动(非价格促销)可改善商品市场需求.用Bm表示零售商用于促销的资金,用D(Bm)表示在促销资金为Bm下市场需求的增量.基于此,在零售商促销下商品的市场需求可模型化为D(Bm)+ξ.一般地,促销资金越多,对市场需求的改进力度越大,但促销对市场需求的改善具有边际递减效应,即满足D′(Bm)>0,D′′(Bm)<0 且D(0)=0,其中D(0)=0 表示零售商不实施促销活动下市场需求的改善为0.
当采购和促销资金分别为Bc和Bm时,零售商可实现的利润为
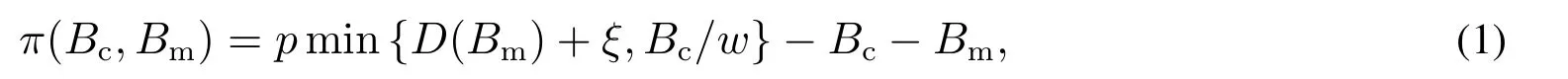
用E[π(Bc,Bm)]表示零售商利润的数学期望.下面将分别给出零售商在资金充裕和资金短缺下的最优运营策略,其中资金短缺又包括不融资和外部融资两种情形.
2.1 资金充裕模型
零售商面临确定Bc和Bm以最大化E[π(Bc,Bm)] 的优化问题,即
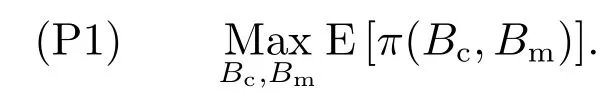
要确保(P1)存在内点解,约定(p −w)D′(0)>1.设是上述问题的最优解,则有
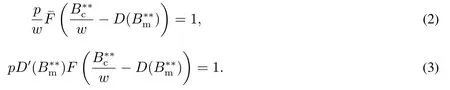
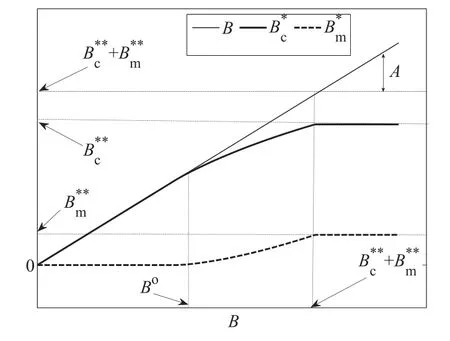
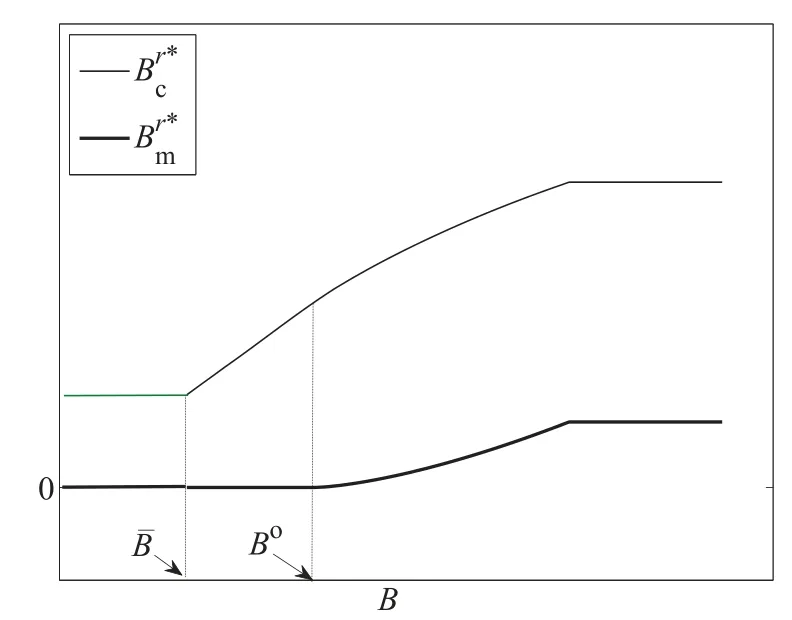
下面简要解释为什么要施加(p −w)D′(0) > 1 这一限制条件.注意到式(2)和式(3)的左侧分别表示的是花在商品采购和促销业务上的最后一单位资金实现的边际收益, 当Q > Q°时, 零售商采购商品的边际收益小于1, 而持有现金的边际成本为1, 因此, 在不开展促销活动下零售商至多采购数量为Q°的商品.当Q ≤Q°时,零售商花费Bm促销资金的边际收益为pD′(Bm)F(Q),因促销的边际效应递减,则有pD′(Bm)F(Q) 定理1无资金约束下,零售商的最优采购资金和促销资金由以下条件联合确定, 即 证明见附录(后文中未给出的证明均列在附录中). 定理1 刻画了无资金约束下采购资金和促销资金的关系,其中最优促销资金由促销对市场需求的改善作用所确定,因(p −w)D′(Bm)表示的是促销资金为Bm时的边际收益,而持有现金的边际成本为1,根据边际收益等于边际成本的原则,可确定最优促销资金.商品采购资金由两部分构成, 一是不促销下最优采购资金wQ°,二是因促销导致的市场增量需额外花费的采购资金wD().根据定理1,如果促销能改善市场需求,那么零售商采购的商品数量将多于不促销的对应情形,即 在现实中,零售商常常面临资金约束,设零售商持有的初始资金为B.零售商的采购和促销资金均需在期初进行支付,本文不考虑零售商在期中将销售回笼资金用于促销活动的情形.下面分零售商不对外融资和对外融资两种情形进行讨论. 2.2.1 不融资情形 当零售商不能从外部获取资金融通时,商品采购和促销活动所需资金只能来自于初始资金.在资金约束下,零售商面临以下优化问题(P2) 在求解(P2)之前,先给出两个引理. 引理1存在B°满足且有B° 引理2设Bc(B),Bm(B)是下面两个方程的解,即 令G(B)=Bc(B)/w −D(Bm(B)),则有,1)Bc(B),Bm(B)和G(B)均是关于B的严格增函数;2)Bc(B°)=B°,Bm(B°)=0 且Bc(B)+Bm(B)≥B°; 3). 根据引理2, 当B≥B°时,如果把所有的资金用于商品采购和促销活动, 且在两者之间进行合理的配置, 即花费在两项活动的资金产生相等的边际收益, 那么随着初始资金增加, 资金运用的边际收益递减.当B 根据引理1 后的讨论,促销资金的边际收益与商品采购数量(或资金)有关.而在零售商促销下,采购资金的边际收益依赖于促销强度(等价地,促销资金):促销资金Bm越多,采购资金Bc实现的边际收益就越大.因此,零售商用于商品采购和促销的资金应相互协调. 求解P2,可得零售商的资金运用策略,相关结果如下. 定理2在不考虑外部融资下,零售商的资金配置决策B∗c和B∗m满足: 1)当B 在不融资下,零售商的资金运用策略如表1 所示. 表1 不融资下零售商的资金运用策略Table 1 The funding operation strategy of the retailer in the absence of financing 图1 反映了不同初始资金下零售商的资金运用策略.当B 图1 不融资下零售商的资金运用策略Fig.1 The funding operation strategy of the retailer in the absence of financing 当B≤B°时,零售商将把所有的初始资金运用于采购商品.在零售商的初始资金十分稀缺下, 即使把所有资金运用于商品采购,相对于既定的市场需求,也是供不应求的,因而没有必要实施促销活动,对应的资金运用策略反映在图1 中B°的左侧. 2.2.2 外部融资情形 假设零售商可向银行等金融机构融通资金.为了集中讨论零售商的融资和运营策略, 假定金融市场充分竞争[17,19,25], 在这一假设下, 可设融资期限为一个经营周期下的贷款利率为r.不失一般性, 约定0 ≤r≤(p −w)/w.为了看清r≤(p −w)/w这一限定条件表达的意义,将其改写为w(1+r)≤p,如果这一条件被违背,零售商融资后采购商品的成本将大于销售价格, 零售商的最优决策将是不融资.在贷款金额为C且利率为r下,零售商分别运用Bc和Bm的资金于商品采购和促销活动可实现的利润为 零售商面临确定贷款金额并将包括初始资金和贷款在内的资金运用于采购商品和促销活动以最大化其期望利润的问题(P3) 设r°满足如下条件:(B°/w) =w(1+r°).令B(r) 满足(B(r)/w) =w(1+r),易证B(r) =wF−1(φ),其中φ=(p −w(1+r))/p.很显然,B(r)是关于r的严格减函数,且有B(r°)=B°.有以下结论. 引理3当且仅当r° 证明要使式(6)中等式成立,由有0< r≤(p −w)/w;由引理1,要使式(6)中的不等式成立, 必然要求 最后利用B(r)的递减性及B(r°)=B°,引理3 得证. 证毕. 引理4当且仅当0 ≤r≤r°时,存在一个B ∈[B°,B∗∗c +B∗∗m]满足 证明根据引理2,要使式(7)中第一个等式成立,必有B°≤B.而由定理1, 又有 注意到由B(r)和(x)的递减性以及G(B),引理4 得证. 证毕. 利用引理3 和引理4,可刻画零售商在外部融资下的资金筹集及运用策略. 定理3在外部融资下,零售商的最优融资Cr∗和资金配置决策如下: 1)如果r >r°,那么(a)当时,则有.2)如果r≤r°,那么(a)当B <时,有(b)当B≥B时,有 根据引理3,当r >r°时,有 当r 表2 外部融资下零售商的资金运营策略Table 2 The funding operation strategy of the retailer in the presence of outer financing 前面的讨论表明, 零售商是否选择贷款依赖于初始资金的丰裕情况和融资的利率, 为了强调这种关系, 使用记号Cr∗(B)>0 和Cr∗(B) = 0 表示在利率等于r且初始资金为B下零售商选择贷款和不选择贷款.定义两个集合A={B|Cr∗(B)>0}以及={B|Cr∗(B)=0}, 根据定理3, 显然有A∩=∅,A∪=Ω,其中∅和Ω分别表示空集和全集. 推论1设B1∈A,B2∈A,则有: 1)如果B 证明直接由定理3 可推得结论. 证毕. 由定理3 和推论1,零售商的资金筹集及运用策略可用图2 和图3 来反映. 图2 反映的是r > r°下的策略.只要B <,零售商就从外部筹集资金,并使借贷资金与初始资金总和等于,然后将完全用于采购商品.当B≥时,零售商不向资金市场筹资,商品采购和促销的资金运用与不贷款时的最优策略保持一致. 图2 零售商的资金运用策略(r >r°)Fig.2 The funding operation strategy of the retailer(r >r°) 当r≤r°时,零售商的融资及资金运用策略如图3 所示.只要B <,零售商就贷款,且贷款金额正好使得零售商的总资金等于;在资金运用一侧,零售商将把数量为的资金投放到商品采购和促销活动中去,并确保两项活动的边际收益相等.当B≥时,零售商不贷款,商品采购和促销的资金运用与不考虑融资下的最优策略保持一致. 图3 零售商的资金运用策略(r ≤r°)Fig.3 The funding operation strategy of the retailer(r ≤r°) Dada 等[3]在不考虑促销下得到以下研究结论:即使存在融资机会,零售商的采购量仍低于理想的最优订购量.根据定理3,只要r >0,就有因此,上述结论在零售商促销下仍然成立.此外, 还有综上,存在融资机会下,零售商将加大采购数量,且在市场利率较低时还将加大促销力度,尽管如此,零售商的采购量和促销强度仍然低于理想值. 2.2.3 比较分析 基于定理2 和定理3,表3 总结了零售商在不融资和外部融资下的资金运用策略. 表3 不融资和对外融资下零售商的运营策略对比Table 1 Comparison of the operational strategies of the retailer in case of no financing and of outer financing 在外部融资下,资金短缺的零售商将采购数量更多的商品,这与Dada 等[3]以及陈祥锋等[14]在不考虑促销下的研究结论是一致的.虽然融资能增加零售商的订购量, 但对促销的影响则更为复杂, 当利率较高(r > r°)时,零售商的促销策略在不融资和外部融资下相同,即融资不增大零售商的促销力度;当利率较低(r≤r°)时,相对于不融资的情形,在外部融资下零售商将花费更多的资金用于促销. 定理4如果且E[πr∗] ≥E[π∗],其中严格不等式至少在B的一个区间成立. 存在融资机会下,零售商将会借助贷款等方式缓解资金短缺问题,这将导致外部融资下的资金运用大于不融资的对应情形.如果零售商是理性的,外部融资可实现的收益必定大于(至少不小于)融资成本,因此,外部融资下的期望收益大于(至少不小于)不融资的对应情形.陈祥锋等[14]在不考虑零售商促销下分析了外部融资对供应链绩效的影响,得到了融资服务有助于改善运营绩效的结论,这与定理4 是一致的. 定理2 和定理3 表明零售商的初始资金会影响其运营策略,下面的结果进一步揭示了初始资金的多寡对零售商策略及其收益的影响. 定理51)在区间均是关于B的非减函数.2)在区间E[π∗]关于B严格增且严格凹,而E[πr∗]是关于B的严格增的凹函数,且有 (a)如果r >r°,当B <时,有当B >B时,有 (b)如果r≤r°,当B <时,有 在资金短缺下,如果零售商没有融资机会,其拥有的初始资金越多,就会将更多的资金运用于商品采购和促销活动.如果存在外部融资机会,当零售商的初始资金严重短缺时,零售商将通过金融机构获得外部资金支持,在这种情形下,零售商拥有的初始资金数量对资金运用策略没有影响;尽管如此,如果零售商的初始资金达到一定的规模,以至于不会利用外部融资渠道,那么零售商的资金运用策略与不融资的情形是一样的,在这种情形下,初始资金越多,零售商用于商品采购和促销活动的资金也越多.杜文意等[24]也得到了这一结论,他们讨论的情形对应于r≤r°且B ∈(0,)的情形,是本文的一个特例.在资金短缺下,无论是否存在融资机会,零售商的初始资金越多,可实现的收益就越大.如果没有融资机会,零售商的资金运用均来源于初始资金,由于资金运用遵循边际收益递减规律,在资金的运用实现最优之前,资金运用实现的边际收益大于持有现金可实现的收益.因此,在资金短缺下,初始资金越多,实现的收益越大,且随着初始资金的上升,它对零售商收益的影响递减.如果存在融资机会,理性的零售商只有在融资实现的收益大于融资成本时才会选择外部融资,相对于自有资金,融资额外带来的资金成本为r,因此,初始资金越多,零售商实现的收益就越大,且每增加一单位初始资金,零售商的期望收益可增大r单位.在外部融资下,初始资金对零售商收益的影响小于不融资的对应情形,这是因为零售商可借助外部融资缓解资金短缺问题,因而对初始资金的依赖程度相对较弱. 除了初始资金,金融市场利率对零售商的决策和收益也有重要影响.下面讨论这一问题. 引理5和均是关于r的严格减函数. 证明将隐函数定理分别运用于式(6)和式(7)可得相关结论. 证毕. 利用引理5,可得以下结论. 定理61)当r >r°时,和Cr∗是关于r的减函数,独立于r的变化;当r 如果资金严重匮乏,金融市场利率越高,融资成本越大,零售商越趋向于减少贷款总额,对应地,减少商品采购和促销活动的资金运用.如果资金相对不足,利率又足够高以至于零售商的最优选择是不实施贷款,那么利率的微小变化对零售商的资金运用就不会产生任何影响. 如果零售商实施贷款(Cr∗>0),那么利率对零售商的收益具有负面影响,且利率每提高一个单位,贷款成本上升Cr∗个单位,因而期望收益减少Cr∗个单位.随着利率的上升,零售商的贷款金额下降,Cr∗减小, 直到Cr∗= 0 为止.因此, 利率对零售商收益的负面影响程度随利率的上升而递减.如果资金相对充足,或者利率过高,以至于零售商放弃贷款,那么利率的微小变化对零售商的收益没有影响.特别地,如果零售商资金充足=0,利率的变化不影响零售商的收益,这与直觉相符. 下面讨论销售价格对零售商决策和收益的影响.有下列结论. 引理6和关于p严格增,B°独立于p的变化,和关于p严格增. 证明略. 定理71)是关于p的增函数. 2)E[π∗]和E[πr∗]关于p严格递增且凸,且 在资金短缺下,如果没有融资机会,销售价格的改变对零售商的资金运用策略没有影响,因为价格的改变对商品采购资金和促销资金的收益具有相同的影响,因而采购资金和促销资金的最优配比不变.尽管如此,销售价格的上升增大了商品采购和促销活动的资金收益,因此,如果存在融资机会,零售商将筹集更多的贷款用于上述两项活动.在资金充足下,随着销售价格的上升,资金运用的边际收益上升,零售商将同时增大商品采购和促销活动的资金运用. 如果没有融资机会,在资金短缺下,销售价格的上升不改变资金运用策略,因而最终实现的商品期望销量保持不变,销售价格每上升一个单位,利润按商品销量成比例地增加,因而是线性的; 在资金充足下,销售价格的上升诱导零售商增大商品采购和促销力度,最终实现的商品销量上升,销售价格的上涨对利润的影响有两个方面,一是单位商品边际收益的增加,二是商品销量增大对利润的正向影响,两者的共同作用使得零售商的利润关于销售价格递增.如果存在融资机会,在资金短缺下,销售价格上升诱导零售商加大融资力度,并相应地加大商品采购和促销力度,其对利润的影响也是凸增的.除非资金充足,否则,初始资金越多,销售价格对利润的影响程度越大.在资金短缺下,如果没有融资机会,随着初始资金的增加,零售商将加大资金运用力度,商品期望销量随之增加,销售价格对利润的影响程度上升;如果存在融资机会,在资金严重短缺下,借助对外融资,可确保资金运用策略不变,商品期望销量不变,销售价格对利润的影响程度不变.在资金充足下,价格的变化不改变零售商的资金运用策略,销售价格对利润的影响不再随价格的变化而变化. 采购价格的变化对零售商采购资金运用策略的影响比较复杂,在一般情形下不能得到一致的结果,但对采购商品数量的影响是确定的.令有下列结论. 引理7关于w严格递减.如果随机变量ξ具有递增失败率,那么B°和Bc(B)均是关于w的严格增函数,而Bm(B)和是关于w的严格减函数. 定理8若随机变量ξ具有递增失败率,则关于w严格递减,且E[π∗]和E[πr∗]均是关于w的严格减函数. 采购价格上升导致采购成本上升,零售商随之减少商品采购数量.面临同样的市场需求,零售商将减少促销投入,否则将导致对市场的激励过度.在资金充足下,由于采购价格上涨,采购资金数量是不确定的,而在资金相对短缺且不对外融资下, 零售商将把所有初始资金运用于商品采购和促销活动, 由于促销资金减少,因而用于商品采购的资金增大(但采购资金增大的程度小于采购价格上涨的程度,商品采购数量下降).采购价格上升,每采购一单位商品实现的边际收益(利润)减少而采购商品的数量为零售商利润减少量为两者的乘积.在资金充足下,初始资金的变化不改变采购商品数量也不改变采购资金的边际收益(恒等于1),因此,采购价格对利润的影响程度不随初始资金的变化而变化.在资金短缺下,随着初始资金的增加,采购商品数量增加,但采购资金的边际收益递减,两者对利润的影响方向正好相反,且在一般情形下不能确定两者之中谁对利润的影响程度更大. 在外部融资下,给定销售价格和采购价格不变,零售商是否融资依赖于初始资金的丰裕情况、贷款利率以及市场的需求分布.给定市场需求分布,零售商的融资决策取决于初始资金及贷款利率两个因素.直觉上,初始资金充足则不必融资,比如当时;而初始资金不足则可能从资金市场拆借资金.尽管如此,相对于初始资金,借贷资金的使用成本更高(初始资金的边际使用成本为1而借贷资金的边际使用成本为1+r).如果初始资金充足,零售商将把资金使用到边际收益等于1 为止,但在资金短缺下,根据边际收益等于边际成本的决策准则,零售商的资金运用将止于边际收益等于1+r,前提是其能够以利率r筹集到相应的资金.除了初始资金这一影响因素之外,借贷市场的利率是另一个影响零售商融资决策的重要因素,一般地,借贷市场的利率越高,零售商越趋向于不融资或少融资,而借贷市场的利率越低,零售商越趋向于融资. 推论2如果r=0,则有如果r=(p −w)/w,则有B=0. 证明直接由引理3 和引理4 可推得结论. 证毕. 如果融资没有成本,零售商使用借贷资金的成本与初始资金相同,那么零售商总趋向于贷款,除非初始资金相当充足.反之,当贷款利率r很高,以至于w(1+r)=p,借助外部融资来经营商品没有利益,零售商将不对外融资,即使初始资金十分匮乏.很显然,r=0 对应基准模型,而r≥(p −w)/w对应不融资情形. 在不考虑融资的情形下,零售商是否促销依赖于初始资金的丰裕情况、市场的需求分布以及促销对市场改善的作用.根据前文的讨论, 零售商促销的资金临界点为B°, 当且仅当B > B°时, 零售商促销.根据B°的定义,容易表明B°关于D′(0)递减,既然D′(0)表示第一单位促销资金对改进市场需求的作用,当其增大时,零售商采取促销活动的可能性上升,这一结论符合直觉.相对于日常用品和普通功能性用品,创新性产品和时尚用品的促销活动对市场需求的改善效果更佳,经营这类产品的商户更有激励采取促销活动,这与商业实践相吻合.在融资下,零售商的促销决策还依赖于金融市场的利率.直觉上,借贷市场的存在将增大零售商促销的可能性,且市场利率越低,零售商促销的可能性越大.但理论分析表明,上述直觉并不成立.当r > r°时,如果零售商在不融资下的最优决策是不促销,那么零售商不会借助融资来开展促销活动,即借贷市场的存在不改变是否促销的决策,不增大零售商实施促销活动的可能性.尽管如此,当r < r°时,无论初始资金如何,零售商总是趋向于实施促销活动,且促销的力度依赖于市场利率:市场利率越低,促销力度就越大.前面的讨论有助于解释下面的经济现象.第一个经济现象:经营生活必需品或大宗商品的零售商基本不开展促销活动,经营日常用品和普通功能性用品的零售商也很少实施促销活动,或者即使促销但力度很小,而经营创新性产品和时尚用品的零售商则会花较多的资金进行商品促销.这一经济现象可解释如下:由于经营不同性质商品的零售商面临不同的市场,这些市场对促销的敏感程度差异巨大,在不同商品市场下,同样的促销资金对市场需求改善作用的效果迥异.第二个经济现象是规模较大的零售商更多地开展促销活动,这有两个原因,一是规模较大的零售商资金相对充裕,二是促销资金的边际收益与商品的库存数量有关,而规模较大的零售商其商品库存数量更大.第三个经济现象:在货币扩张政策下,零售行业相对繁荣,零售商不仅采购更多数量的商品,而且加大力度开展形式多样的促销活动.这是由于通货膨胀,商品价格上涨,且借贷市场利率降低,融资成本变小,很多中小零售商不惜通过融资的方式也要实施促销活动以赢得商业竞争. 随着市场竞争的加剧和需求不确定性的增加,零售商将更多地借助促销手段来获得竞争优势.在初始资金充足下,零售商拥有更多的资源来实施促销活动,但广大中小零售商常常面临资金约束,在此背景下,中小零售商在每个运营周期,尤其是在创业初期和快速发展时期(在这两个时期零售商尤其需要通过促销活动来打开市场销路),都需对资金运用及筹集等问题进行决策.本文在不融资和外部融资两种情形下,分别刻画并比较分析了零售商在不同初始资金状况下的最优订购、促销和融资策略.刻画了零售商促销和融资的临界条件,讨论了零售商的初始资金、市场利率、销售价格和采购价格对零售商运营策略和收益的影响.最后,利用研究结果解释了与促销有关的部分经济现象. 本文是在金融市场完全竞争假设下进行的研究,市场利率外生给定,下一步可考虑策略性金融机构与零售商的博弈问题.此外,在融资渠道方面,本文仅讨论了外部融资下零售商的决策问题,供应链内部融资下的契约设计问题也值得进一步研究. 附 录 定理1 的证明E[π(Bc,Bm)]关于Bc和Bm的海塞矩阵 注意到D′′(Bm)<0,因此,H是严格负定阵.零售商关于确定Bc和Bm以最大化E[π(Bc,Bm)]的优化问题存在唯一最优解.上述极大化问题的一阶最优条件给出式(2)和式(3),将式(2)和式(3)简单变形并注意到可完成证明. 证毕. 引理1 的证明考虑两个函数wD′(0)F(B/w)和前者关于B递增,后者关于B递减,由 并注意到F()的连续性,必定存在B°满足 下证B° 引理2 的证明1)先证明Bc(B)和Bm(B)关于B严格增.注意到Bc(B)和Bm(B)满足式(4),因而有 上面等式左侧的式子是关于Bc(B)的严格减函数和Bm(B)的增函数, 而右侧左子是关于Bc(B) 的严格增函数和Bm(B)的减函数,因Bc(B)+Bm(B)=B, 用反证法即可证明Bc(B)和Bm(B)关于B严格增. 下证G(B)B的增函数.将上面的等式改写为 使用隐函数定理,对上式两边求关于B的一阶导数,有 简单的恒等变换,得 注意到D′′(Bm(B))<0 以及Bm′(B)>0,故有G′(B)>0. 2)用反证法证明Bc(B)+Bm(B)≥B°,假设Bc(B)+Bm(B) 这与式(4)矛盾. 最后, 容易验证Bc(B°) =B°和Bm(B°) = 0 是方程(4)和方程(5)联合确定的解.下证它是唯一解, 如若不然, 则有Bc(B°) 3)与2)的证明类似,略去. 证毕. 定理2 的证明设和为P2 的最优解.P2 的K-T 条件可表示为 下面通过对K-T 条件的讨论来求解P2.首先排除µc>0 的情形, 如果µc>0, 则有= 0, 由式(F2), 有µm=1+λ>0,故有=0,这显然不是最优解.基于此,后文在µc=0 下进行讨论,分四种情形. 1)λ=0,µm=0. 在这种情形下,式(F1)和式(F2)分别简化为式(2)和式(3),因而有 2)λ=0,µm>0. 由µm>0 可得=0,由式(F1)可得式=wQ°,因此式(F2)可简化为 这与假设(p −w)D′(0)>1 相矛盾. 3)λ>0,µm>0. 4)λ>0,µm=0. 在这种情形下,式(F1)和式(F2)简化为 注意到λ>0,通过比较式(2)和式(F9),可得 利用这一结果,由式(3)和式(F10)及D(·)的凹性,可证再将这一结果置入式(F11),则有这等价于最后,利用引理2 以及λ>0,又有综上,可得 证毕. 定理3 的证明设是P3 的最优解.P3 的K-T 条件为 与定理2 的证明类似,有关µc=0 的讨论仍然是成立的.下面分κ=0 和κ>0 两种情形进行讨论. 第一种情形:κ=0. 如果κ= 0,则由式(F14),有λ=r >0.如果零售商进行了贷款,那么资金约束将起作用, 即零售商将把包括初始资金和贷款在内的所有资金用于采购商品和实施促销活动,不允许存在闲置资金. 1)κ>0. 由κ>0,有=0,与λ=r >0 相结合,则有且由式(F12)和式(F13)可得 2)µm=0. 根据式(F12)和式(F13),可由以下三式联合确定, 即 第二种情形:κ>0. 在这种情形下,有Cr∗=0,即零售商的最优决策是不贷款. 1)λ=0,µm=0. 此时, 式(F12)和式(F13)分别简化为式(2)和式(3), 故有式而由Cr∗= 0 及λ= 0, 必有 2)λ=0,µm>0. 由µm>0 可得=0,由式(F12)可得=wQ°,式(F13)还原为(p −w)D′(0)=1−µm<1,这与假设矛盾. 3)λ>0,µm>0. 由式(F14)以及κ >0,有λ < r;由µm>0,又有= 0,注意到λ >0,则有=B.将上述结果与式(F12)和式(F13)相结合可得 4)λ>0,µm=0. 当µm=0 时,由式(F12)和式(F13)可得 因λ>0,故有根据引理4,上式可简化为 如果r >r°,由引理2,则有如果r≤r°,由引理3,可得证毕. 定理4 的证明有关的结论可直接由定理2 和定理3 得到.下证E[πr∗]≥E[π∗]. 注意到Cr∗在B的某些区间大于零,在这种情形下上述推导中的不等式为严格不等式,因此E[πr∗]≥E[π∗]至少在B的一个区间严格成立. 证毕. 定理5 的证明1)利用定理2 和定理3 可直接推得结论. 2)由包络定理,有 上面第二个等式由式(F13)及µc= 0 得到.当时, 由定理2 证明中的第1) 种情形, 有λ= 0, 故有时,由定理2 证明中的第3)和4)种情形,有λ>0.由r°的定义=w(1+r°),可得 由式(F26),又有 当00,与式(F27)相结合可证:在区间 E[πr∗]关于B在区间严格递增和凹的证明是类似的,证明略. 1)注意到当B >时,有E[πr∗]=E[π∗], 故有 当B < 由定理3 证明中的(1.1),有 综上,有 其中第二个等式来自于式(6)以及 2)与第1)种情形的证明类似,略. 证毕. 定理6 的证明1)直接由定理3 和引理5 可推得结论. 定理7 的证明1)由定理2、定理3 和引理6 可直接推得结论. 2)由包络定理,有 引理7 的证明在证明之前,首先给出一个引理. 令S(ξ)=F(ξ)−z(ξ)(ξ+k),其中z(ξ)= 引理8如果随机变量ξ具有递增失败率,那么S(ξ)≤0, 且当ξ >0 或者k >0 时,有S(ξ)<0. 引理8 的证明由S(0)≤0 以及 则有S(ξ)≤0,且当ξ >0 或者k >0 时,有S(ξ)<0. 证毕. 下面证明引理7.1)将隐函数定理分别运用于式(2)、式(3)、式(6)及式(7)可完成第一部分的证明. 下证第二部分.首先证明Bm(B)关于w严格递增.利用引理2,将式(4)和式(5)改写为 对式(F30)两侧求关于w的一阶偏导数,则有 由式(F31),利用这一结果,并由可得 将上式置入式(F32),移项后得到 第一个等式的左侧小于零,由引理8,又有S(G(B)) ≤0,其中对任意B≥B° >0,有S(G(B))<0.因此,相结合,可证 由Bc(B)+Bm(B)=B,可得由B°=Bc(B°),又可得证毕. 定理8 的证明直接由定理2、定理3 和引理8 可推得第一部分的相关结论. 下证E[π∗]和E[πr∗]关于w递减.由包络定理,有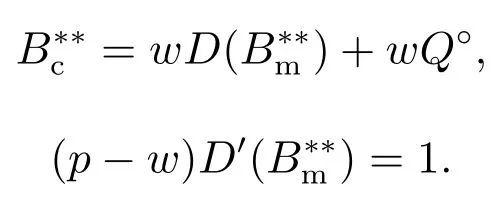
2.2 资金短缺模型

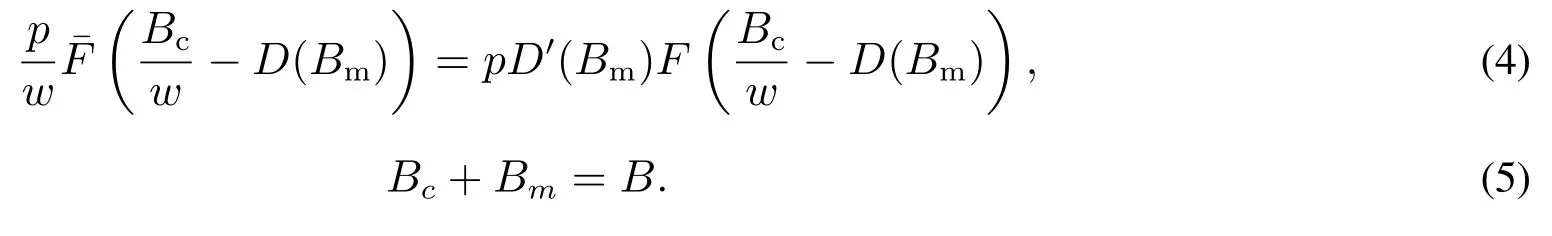
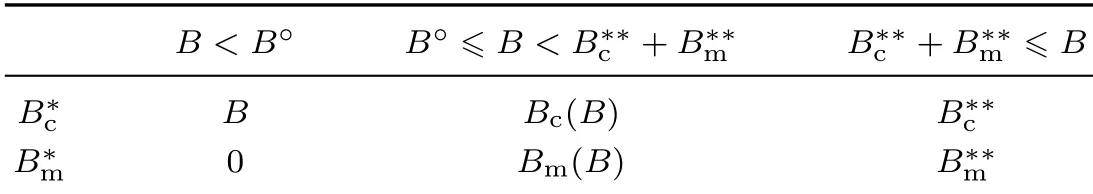
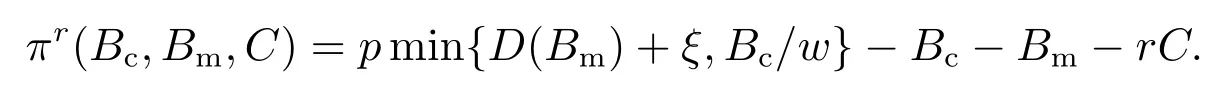
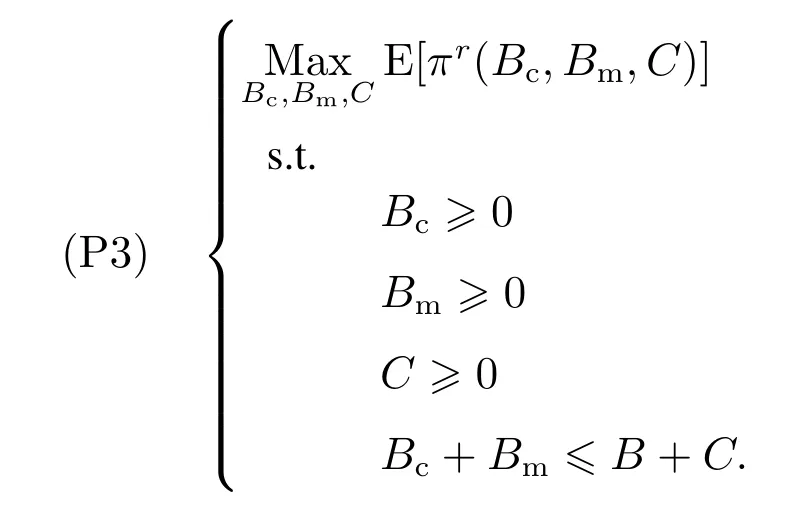
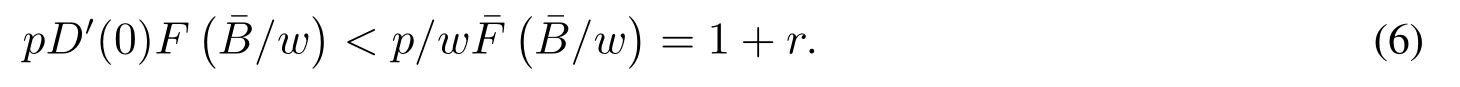
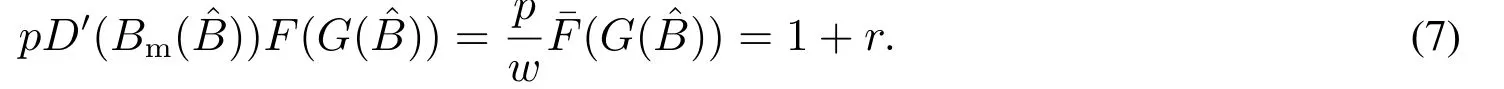
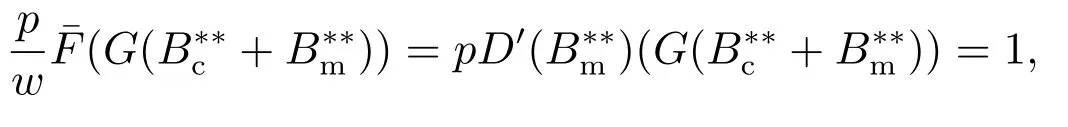



3 比较静态分析
3.1 初始资金对零售商策略和收益的影响分析
3.2 金融市场利率对零售商策略和收益的影响分析
3.3 销售价格对零售商策略和收益的影响分析
3.4 采购价格对零售商策略和收益的影响分析
4 进一步讨论
4.1 零售商的融资决策
4.2 零售商的促销决策
5 结束语