超可加对策的边际等分集

张 莉，常丽娜

（长治学院 数学系，山西 长治 046011）

1 引言

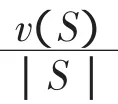
文章将边际主义原则与平均主义原则加以结合，针对超可加对策提出了一种新的集合解—边际等分集。证明了边际等分集中的每一个解都满足有效性与个体理性，也就是说它们都包含在分配集中，由此可见，边际等分集是比较合理的分配方式。其次，文章给出了边际等分集的分配单调性，越早瓜分收益的参与人得到的收益越多，以此鼓励参与者积极为大联盟的形成做贡献。最后，证明了边际等分集是均分核心的子集。

2 预备知识

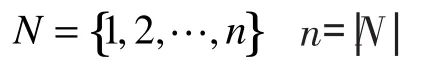
一个对策 v 是超可加的，若 v（S∪T）≥v（S）+v（T）对所有的且都成立。本文中没有强调的对策v均是超可加对策。

1972年Selten提出了等分配核[8]的概念

3 主要结论

在给出边际等分集之前，我们先来定义一个序列博弈。

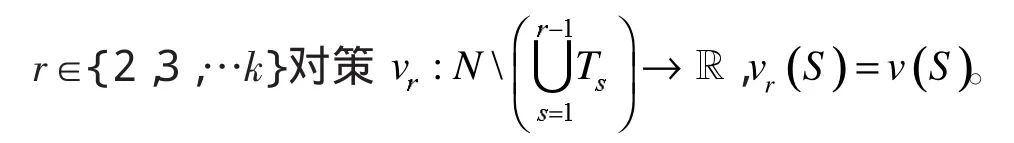
定义1给出了一个序列博弈，从大联盟N中逐步剔除一些参与者，由剩下的参与者以及他们的特征函数构成新的对策。

定义3 给定一个恰当有序划分π=〈T1，T2，…，Tk〉，基于π的边际等分解

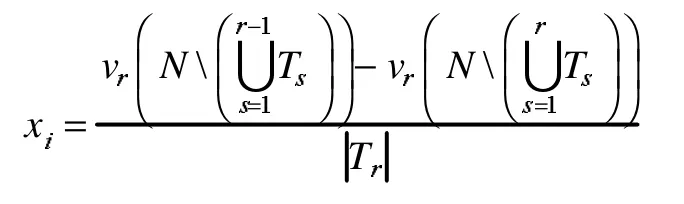
事实上，根据定义1，边际等分解可以表示为

对于一个超可加对策v，可能存在多个恰当有序划分，每个恰当有序划分都可以得到一个边际等分解，那么所有边际等分解的集合，我们称为边际等分集（marginal equal split set），简称 MESS。

为了帮助理解边际等分集的概念，我们先来看两个例子。

例 1 设有合作对策 v，N=｛1，2，3｝，

v（1）=2，v（2）=3，v（3）=1，v（12）=6，v（13）=4，v（23）=5，v（123）=8，

求该博弈的边际等分集。

解：（1）先求每个联盟对于大联盟N的平均边际贡献：

（2）剔除参与者2后对策v2为v2（1）=2，v2（3）=1，v2（13）=4。

所以，T2={1}，x1=3。

（3）剔除参与者1后对策v3为v3（3）=1。

所以，T3={3}，x3=1。

综上所述，该对策的恰当有序划分为π=〈{2}，{1}，{3}〉，其边际等分集 MESS（v）=｛（3，4，1）｝。

例 2 设有合作对策 v，N=｛1，2，3，4｝，

求该博弈的边际等分集。

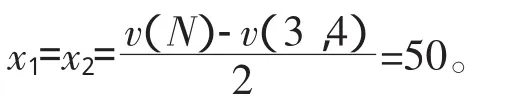
（2）剔除参与者1、2，对策v2为v2（3）=0，v2（4）=0，v2（34）=0。

所以 T2={3，4}，x3=x4=0。

综上所述在恰当有序划分 π=〈｛1，2｝，｛3，4｝〉下，该对策的边际等分解为（50，50，0，0）。

同理考虑所有的恰当有序划分，最终求得该对策的边际等分集

边际等分集是一个集合解，它具有较好的性质，我们可以证明超可加对策的边际等分集是其分配集的子集。

证明：即证对任意的x∈MESS（v），则x∈I（v）。也就是说对任意的x∈MESS（v）都满足有效性与个体理性。

取任意的x∈MESS（v），其对应恰当有序划分〈T1，T2，…，Tk〉。

则

所以x是有效的。

令 i∈Tr，r∈｛1，2，…，k｝

则

其中，第一个不等式是根据边际等分集的定义，第二个不等式是因为对策v是超可加的。

因此，x是个体理性的。

根据边际等分集的分配方式，我们推测越早分到收益的参与者，分得的收益也应该越多。事实上，我们可以证明在超可加对策中，边际等分集满足这样的分配单调性。

性质 6 设 v 是一个超可加对策，〈T1，T2，…，Tk〉是对策v的一个恰当有序划分，则

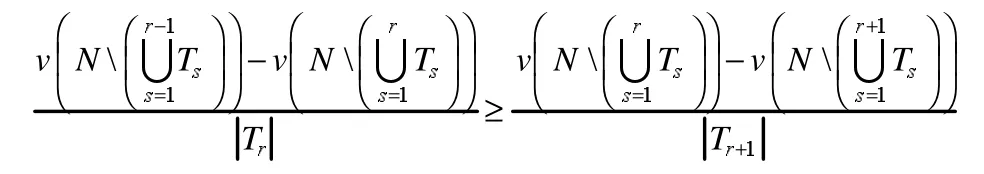
对所有的 r∈｛1，2，…，k-1｝均成立。

证：根据定义

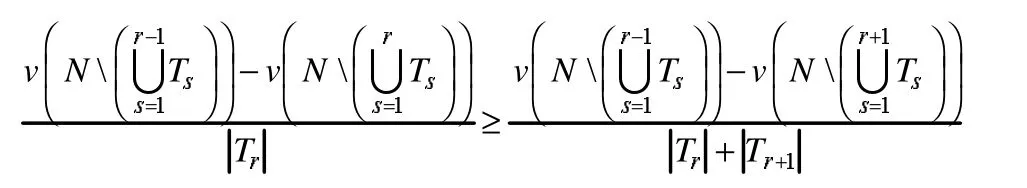
而

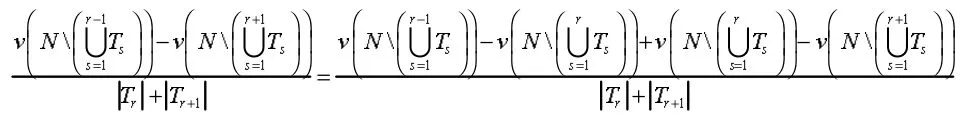
所以

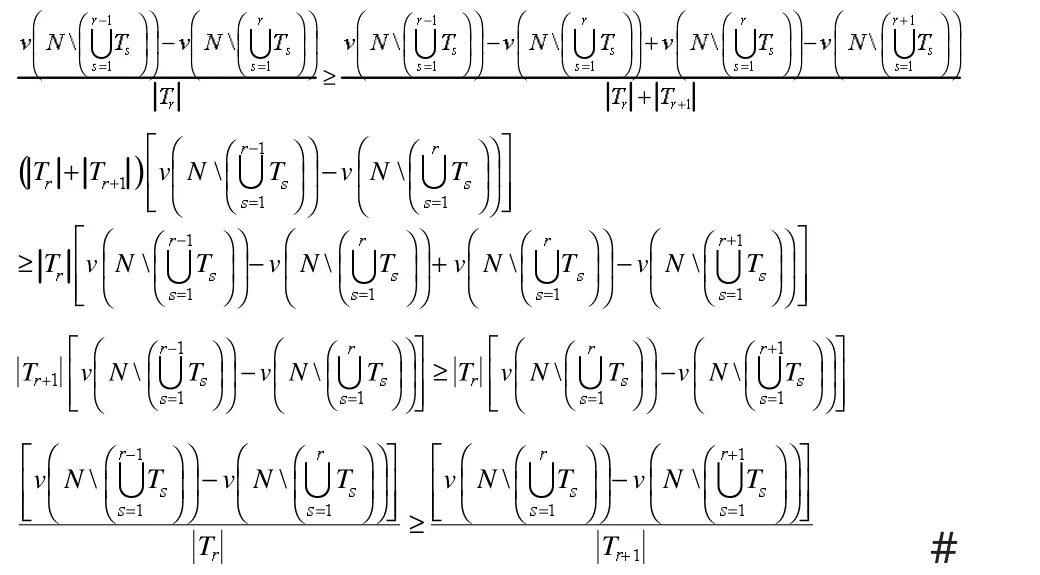
超可加对策的边际等分集与已有的解之间也存在一定关系。超可加对策的边际等分集是等分配集的子集。

令 x∈MESS（v），其对应恰当有序划分〈T1，T2，…，Tk〉。

4 总结

文章结合“边际主义”和“平均主义”原则提出了边际等分集这一集合解，并给出了边际等分集的一些良好的性质，以此说明边际等分集的相对合理性。缺陷在于边际等分集只是针对超可加对策，对于一般合作对策不适用。在接下来的研究中，我们可以结合“边际主义”和“平均主义”提出针对所有合作对策都适用的一般解，并说明该解的公平合理性。