一类埃博拉传染病动力学模型基本再生数的研究

杨静雅

（长治学院 数学系，山西 长治 046011）

1 引言

埃博拉疫情严重影响着国际公共卫生安全。截止2016年4月，西非三国（几内亚、利比里亚、塞拉利昂）埃博拉疫情累计患病人数高达28616人，死亡11310人。继西非埃博拉疫情稳定之后，2018年5月，非洲刚果（金）再次爆发埃博拉疫情。根除埃博拉是一场关乎全人类的持久战与攻坚战。

埃博拉问题受到很多学者的关注。Chowell等[1]利用流行病SEIR模型对刚果和乌干达的埃博拉数据进行拟合，得到基本再生数取值并进行了敏感性分析。Althaus[2]利用SEIR模型计算了西非三国埃博拉基本再生数，基于研究结果呼吁利比里亚加强防控措施。Barbarossa[3]利用模型得到埃博拉疫情早期的基本再生数为1.44，模型预测结果表明了防控措施的重要性。韦爱举等[4]建立了包含动物仓室的埃博拉传染病模型，得到了人群与动物的基本再生数的表达式。

2 预备知识

基本再生数R0是指无控制状态下，在易感人群中引入一个感染者，该感染者在其感染期内产生新的感染个体的均值[5-7]。如果R0<1，表示在感染期内，表明该疾病不会蔓延；如果R0>1时，则该疾病可能在人群中广泛传播[7]。

记Xs为无病状态的集合，即

记Fi（x）为第i个仓室中新出现感染者的比例表示经过其它方式转移到第i个仓室个体的比例表示从第i个仓室移出个体的比例。

假设每个函数关于每个变量是二阶及以上连续可微，则疾病传播模型对应的微分方程组为：

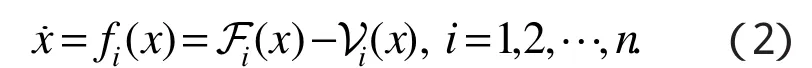
（1）如果 x≥0，则对每个 i=1，2，…，n 均有 Fi，成立。

（2）如果 xi=0，则特别地，如果 x∈Xs，那么对i=1，2，…，m均成立。

（3）如果 i＞m，则 Fi=0。

（4）如果x∈Xs，则m。

（5）如果F（x）=0，则Df（x0）的所有特征值的实部为负。其中，x0是无病平衡点，是x0处的Jacobian矩阵。

定理1.1[8]如果x0是（2）式的一个无病平衡点，并且满足条件（1）－（5），则可以将导数 DF（x0）和DV（x0）进行分块如下：

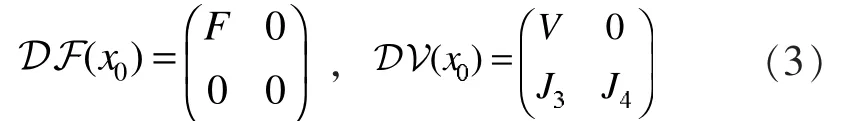
其中，F和V是m阶的矩阵，其定义为：

根据文献[8]，称矩阵FV-1为下一代矩阵，令

其中ρ（A）表示矩阵A的谱半径。

定理1.2[8]考虑（2）式定义的疾病传播模型，f（x）满足条件（1）－（5）。如果 x0是模型的无病平衡点，R0的定义如（5）式所示。当R0<1时，则x0是局部渐近稳定的；当R0>1时，则x0是局部非渐近稳定的。

根据定理1.2，通过计算传染病模型所对应的R0的取值，可以预测疾病的发展趋势。

3 建立模型

假设新生儿及自然原因促成的人口流动不计入人口变化，且已经康复了的埃博拉患者不会再次感染埃博拉病毒。

埃博拉病毒可以通过埃博拉病毒感染者的尸体进行传播。由于非洲地区有拥抱、亲吻、抚摸尸体的风俗，因此，非专业的埋葬、抚摸尸体、参加埃博拉患者的葬礼等都可能感染埃博拉病毒。

文章在已有传染病动力学模型SEIR的基础之上，考虑了埃博拉病毒会由感染者尸体进行传播。通过以上分析，根据埃博拉疫情的特点，建立了SEIRDF模型（见图1）。

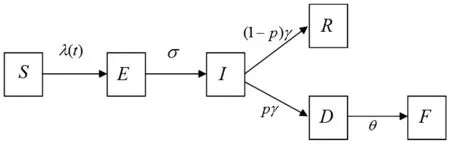
图1 SEIRDF模型示意图Figure.1:State transitions for individuals in the SEIRDFmodel

S表示易感人群，E表示已被埃博拉病毒感染，但尚未表现出症状且不具传染性的潜伏状态的人群，I表示感染埃博拉病毒的人群，R表示感染埃博拉病毒后康复人群，或感染埃博拉病毒死亡后不具有传播性的人群，D表示具有传播性的感染埃博拉病毒死亡者，F表示感染埃博拉病毒死亡后进行埋葬的人群。

综上所述，得到图1所示的埃博拉病毒传播动力学模型为：

4 基本再生数的计算

通过对SEIRDF模型所对应的微分方程（公式6）来计算基本再生数R0。将方程改写为：

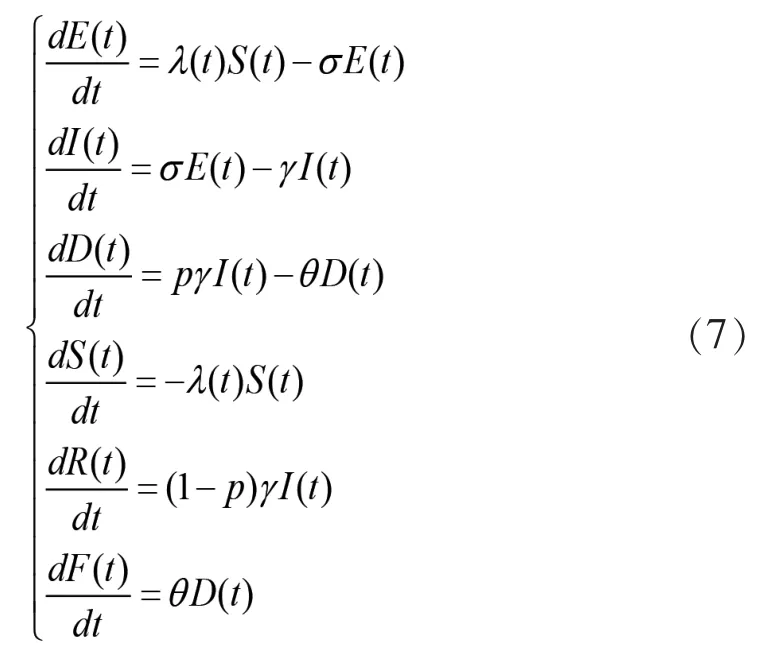
x=（E，I，R，S，D，F）T，感染的仓室为 E，I，D，所以m=3。则

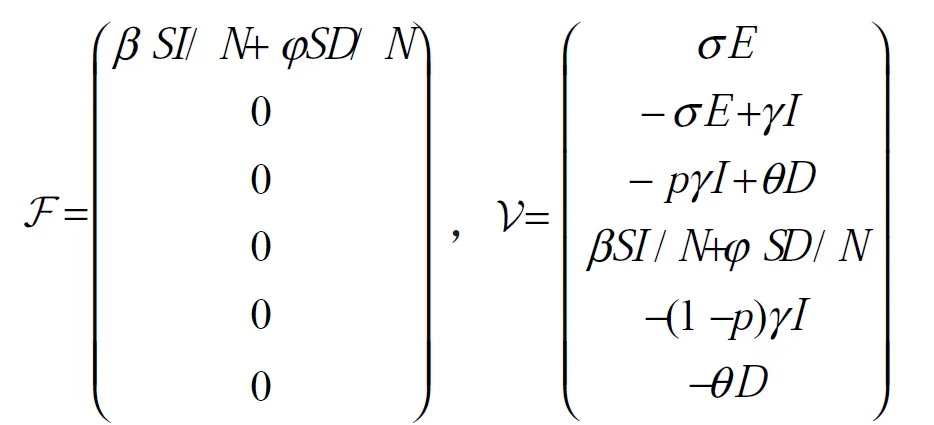
一个无病平衡点为 x0=（0，0，0，S0，0，0）T，则

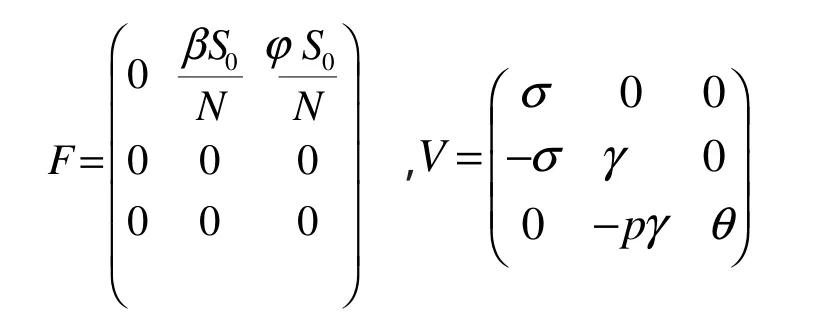
利用逆矩阵的求解方法，得

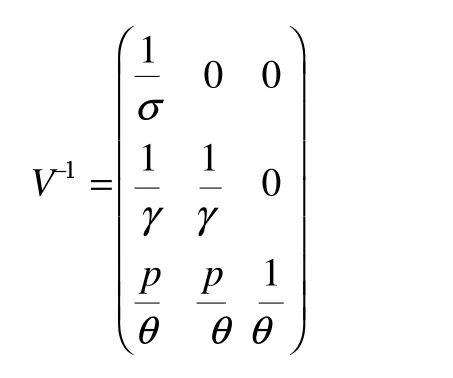
所以，

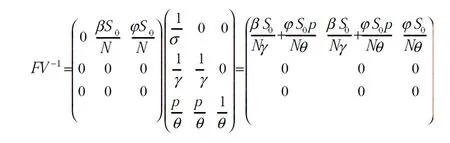
则

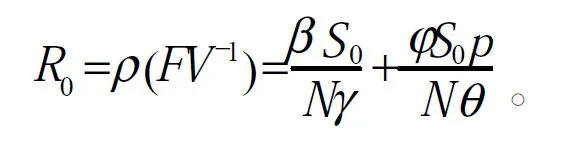
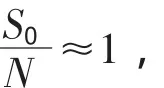
由此可以计算

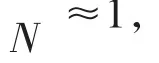
由此可以计算