智能RGV的动态调度策略

贾武艳，王慧蓉

（长治学院 数学系，山西 长治 046011）

1 引言

RGV（Rail Guided Vehicle，有轨制导车辆）是一种无人驾驶、能在固定轨道上自由运行的智能车。它能根据指令自动控制移动方向和距离，并自带一个机械手臂、两只机械手爪和物料清洗槽，能够完成上下料及清洗物料等作业任务。可有效提高了加工效率，在智能加工系统中起着重要的作用。具体智能加工系统的示意图如图1。

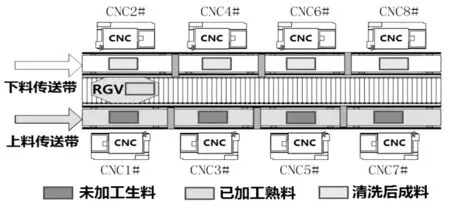
图1 智能加工系统示意图

2 动态任务调度问题

2.1 要解决的问题

（1）在每台CNC上安装同样的刀具，只有一道工序的物料可以在任意一台CNC上加工完成，在一班次的连续作业八小时下，生产出多少成料？

（2）在完成第一道、第二道工序的CNC上分别安装不同的刀具，每个物料的第一和第二道工序分别由两台不同的CNC依次加工完成，在一班次的连续作业八小时下，生产出多少成料？

针对上述两个具体问题给出两各不同条件：一是写出RVG动态调度模型和求解相应的算法；二是在CNC在加工过程中会发生概率大约为1%的故障的情况下，给出以下两种情况的RGV动态调度模型和求解相应的算法。

2.2 模型假设

①假设题目给出的CNC工作时间是有效的、合理的；

②假设加工所有物料的速度是均匀的，恒定的；

③假设传送带运行速度很快，可忽略不计；

④假设每个CNC只能运输一件物料；

⑤假设CNC在加工物料过程发生故障时，故障不会发生在首轮上料过程中。

1.3 符号说明

xi是 RGV移动个单位所需的时间（i=1，2，3）；

m是CNC加工完成一道工序的物料所需的时间；

n是CNC加工完成一个两道工序的第一道工序所需的时间；

l是CNC加工完成一个两道工序的第二道工序所需的时间；

y是RGV为CNCj一次上下料所需时间（j=1，3，5，7）；

z是RGV为CNCk一次上下料所需时间（k=2，4，6，8）；

w是RGV完成一次物料的清洗作业所需时间；

a是循环一次时，RGV移动1个单位的次数；

b是循环一次时，RGV移动2个单位的次数；

c是循环一次时，RGV移动c个单位的次数；

t为首次上料结束后，循环过程中相邻两次到达第一个上料位置的时间。

3 模型的建立与求解[1-3]

3.1 模型一的建立与求解

3.1.1 一道工序的物料加工作业的优化模型分析

（1）模型分析

①在协作时间内，RGV在一次循环中，路径最短时方为最优。

②在循环中，8个CNC必须协作工作，即首次上料时，8个CNC均要上料。因此，无论怎么上料，上料时RGV所走的路径必须大于6个单位距离。

③8个CNC上料完成，途中需停留6次，RGV每运行一次均要停留一次。

④如果RGV在进行完一次循环，每个CNC均未发出需求或下料信号时，RGV处于等待状态。直到信号出现时，RGV进行智能操作。

（2）运行路径

①上料阶段：在每个CNC空闲时，先进行随机上料，直到8个CNC均处于工作状态，回到第一个上料的CNC前，等待。

②循环阶段：开始按照上料的顺序依次下料上料。

（3）具体符号表示

假设t表示首次上料结束后，循环过程中相邻两次到达第一个上料位置的时间。那么，如果t＜m+y时，则需要等待m+y-t秒；如果t≥m+y时，则在RGV到达第一个上料位置时，该CNC已在等待。

3.1.2 模型一的求解

RGV循环一次的清洗时间：t1=8 w；

RGV循环一次的上下料时间：t2=4（y+z）；

循环一次RGV移动所需要的时间：t3=ax1+bx2+cx3；

循环过程中，RGV到达初始位置的时间：t1+t2+t3；

根据上述分析建立线性规划模型来求解一道工序的物料加工作业的最优值。建立模型如下：

目标函数：tmin=t1+t2+t3

决策变量：a，b，c

8小时中能加工物料的个数为

当max[m+y，t]取到最小时，f最大，即8小时中加工物料的个数最多，利用MATLAB软件求得最优结果。

3.2 模型二的建立与求解

3.2.1 两道工序的物料加工作业的优化模型的分析

（1）问题分析

①（设计CNC方面）：因为该物料需要两步才可完成，所以需要考虑各个CNC负责的相应工序。

②（运行过程）：即在设置好CNC分别负责哪道工序后，使得RGV进行随机上料，而后循环，使得RGV运行的总路径最短。此时为最优解。

③只有设计最优和运行最优时，在8小时内生产物料最多。

（2）分析结果

（设计最优）CNC1#，CNC3#，CNC5#，CNC7#负责第一道工序。

CNC8#，CNC6#，CNC4#，CNC2#负责第二道工序。

（路径最优）（其中给 CNC i上料记为 A（i），给CNC i下料记为 a（i），当然，除了第一次上料外，以后的上下料同时进行）

第一阶段（上料过程） A（1）-A（3）-A（5）-A（7）-等待一段时间。

第二阶段（循环过程）-a（1）-A（2）-a（3）-A（4）-a（5）-A（6）-a（7）-A（8）-等待一段时间或直接上下料。

3.2.2 模型二的求解

RGV循环一次的清洗时间：t1=4 w；

RGV循环一次的上下料时间：t2=4（y+z）；

循环一次RGV移动所需要的时间：t3=3x1+x3；

循环过程中，RGV到达初始位置的时间：t=t1+t2+t3；其中，t越小，模型越优。

8个小时加工两道工序物料的个数：

3.3 模型三的建立与求解

3.3.1 一道工序的物料加工作业且考虑故障时的优化模型的分析

由模型一可知，当加工只有一道工序的物料时，沿路径 CNC1#，CNC3#，CNC5#，CNC7#，CNC8#，CNC6#，CNC4#，CNC2#的顺序加工时RGV运行总路径最短。其中每个CNC均可加工。运行示意图如下：（其中给 CNC i上料记为 A（i），给 CNC i下料记为a（i），当然，除了第一次上料外，以后的上下料同时进行）

第一阶段：（上料过程）A（1）-A（3）-A（5）-A（7）-A（8）-A（6）-A（4）-A（2）-等待一段时间。

第二阶段：（循环过程）a（1）-a（3）-a（5）-a（7）-a（8）-a（6）-a（4）-a（2）

模型分析如下。

①优化：假设故障不会发生在上料过程中。

②故障出现在循环中的任意一段中，而实际上CNC中时刻有物料，故每次故障均有8个作废。

③因为故障发生的概率为0.01，所以每加工100次平均有1次故障，而每个CNC每次加工一个物料。

④每次故障发生时均要维修并重新依次上料。

3.3.2 模型三的求解

在8小时只加工一道程序物料能加工数目：x；

在8小时只加工一道程序物料时出现故障次数：0.01x；

由于出现故障废掉的时间：0.01（600+x+y）～0.01（1200+x+y）秒；

RGV循环一次的清洗时间：t1=8w；

RGV循环一次的上下料时间：t2=4（y+z）；

循环一次RGV移动所需要的时间：t3=6x1；

循环过程中，RGV到达初始位置的时间：t=t1+t2+t3；其中，t越小，模型越优化，可得结果如下：

所以8小时能加工的物料数目范围为x2≤x≤x1。

3.4 模型四的建立与求解

3.4.1 两道工序的物料加工作业且考虑故障时的优化模型的分析

由模型二可知：当只加工两道工序的物料时，沿以下顺序加工时RGV运行总路径最短。其中CNC1#，CNC3#，CNC5#，CNC7#加工第一道工序，CNC8#，CNC6#，CNC4#，CNC2#加工第二道工序。运行示意图如下：（其中给CNC i上料记为A（i），给CNC i下料记为 a（i），当然，除了第一次上料外，以后的上下料同时进行）

第一阶段：（上料过程）A（1）-A（3）-A（5）-A（7）-等待一段时间。

第二阶段：（循环过程）a（1）-A（2）-a（3）-A（4）-a（5）-A（6）-a（7）-A（8）-

模型分析如下。

①优化：假设故障不会发生在上料过程中。

②故障出现在循环中的任意一段中，而实际上CNC中时刻有物料，故每次故障均有4个作废。

③因为故障发生的概率为0.01，所以每加工50个均有8个CNC工作100次，平均有1次故障，而每个CNC每次加工一个物料中一个工序。

④每次故障发生时均要维修并重新依次上料。

3.4.2 模型四的求解

在8小时只加工两道程序物料能加工数目：x

在8小时只加工一道程序物料时出现故障次数：0.02x。

由于出现故障废掉的时间：0.02x（600+x+y）～0.02x（1200+x+y）秒

RGV循环一次的清洗时间：t1=4w；

RGV循环一次的上下料时间：t2=4（y+z）；

循环一次RGV移动所需要的时间：t3=3x1+x3；

循环过程中，RGV到达初始位置的时间：t=t1+t2+t3，其中，越小，模型越优化可得结果如下，

所以，8小时能加工的物料数目范围为 x（2）≤x≤x（1）。

4 模型的评价[3]

4.1 模型的优点

（1）模型二是模型一优化之后的结果，更符合实际情形；

（2）运用MATLAB编程实现模型求解，使得求解结果更加精确，减少了人为因素带来的误差；

（3）建立的模型能与实际结合起来，结合实际问题求解，使得模型具有很好的通用性与推广性。

4.2 模型的缺点

（1）模型不考虑传输带的速度，而实际生产中必须考虑；

（2）模型没有考虑RGV的清洗时间，而在实际生产中，熟料在清洗槽中需短暂停留，只不过是远小于机械手将成料放到下料传送带上的时间，这点需要考虑。