社交网络中种子用户分布对产品扩散的影响
汤 胤, 徐永欢, 陈 剑
(1.暨南大学管理学院,广东广州510632;2.中山大学新华学院管理学院,广东广州510507)
1 引 言
自Rogers 从提出创新扩散以来,创新的范围已经从新技术扩大到新产品,新方法,或者新观念、群体现象以及不同个体的行为等,而“扩散”一词则涵盖了有计划性的传播和自发性无计划传播两层含义,并且是一个过程,包含创新、渠道、时间以及社会体系等四个要素[1,2].实践中,移动社交应用市场的竞争已经非常激烈,对于很多新兴的社交应用(app 等各种形式),鉴于其社交属性,用户使用的基础是必须有一定的用户数量,若不能在一定期间内集聚一批用户群体(即形成羊群效应),产品很可能失败.从很多初创项目中观察到,社交应用本身可以满足用户需求前提下,初始种子用户群体在整体人群中比较分散,可能会引起传播障碍,影响用户数增长;而另一方面,若初始种子用户群体非常紧密,难免有覆盖不到的区域,是否同样会影响传播速度?图1 刻画了同样数量种子用户群体在社交网络中的不同分布(x 代表每个小团体中节点的个数,y代表彼此不直接相连的小团体个数),到底哪种更有助于用户增长呢?将这个问题扩大至共享经济应用(如共享单车)中,基于物理空间的初始资源投放也提出了类似的问题.

图1 同样数量种子用户群体(初始资源)在社交网络中的不同分布Fig 1 .Different distribution of seed user of same size in social network
理论研究方面,早期往往采用定性或者问卷调查方法,Bass 混合扩散模型最早采用仿真方式,成功地预测了耐用消费品销量并发现影响创新扩散的重要因素[3].但Bass 模型仅反映宏观特征,对于社会系统内单独个体交互作用后的行为的非线性的涌现缺乏对创新扩散微观机理的考察,而且模型忽略了采纳时间和交互时间,包括其后Bass 模型族系均有这个问题.而创新扩散的本质是大量潜在消费者的微观采纳决策集中涌现为宏观层面的行为模式[4].大量的研究证实,复杂社会网络与创新扩散之间存在相互影响.一方面,社会网络(如人际关系网络)是创新扩散的重要渠道.社会网络中个体对某种创新(社交应用、共享单车应用等)的选择容易受到与之关联的邻居个体选择的影响,即存在网络效应[5−7].宏观的扩散模型无法考虑采纳者的异质性,忽略了微观层面消费者个性与社会交互等特点对产品扩散的影响,从而使其在现实应用中出现了一定的局限.尤其是随着移动互联网的普及以及社会化媒体的出现,使得潜在的消费个体决策行为越来越多地受到来自周边其他个体选择的影响.忽略了这种交互作用,将难以准确的描述和解释具有网络外部效应的创新扩散.
20 世纪90年代以后, 阈值模型、渗流模型、元胞自动机模型、Agent-based 模型以及多智能体模型等开始从微观角度刻画创新扩散的动力学过程,并在创新扩散的前期预测方面体现出有效性和稳定性的特征[8−13].Granovetter 提出的门槛模型(阈值模型)充分考虑了信息接收者的特性和信息传播具有记忆效应,能够更为直观地展示社会系统结构对创新扩散的影响,特别适用于社会动态问题的仿真研究[14,15],如郭静等[16]基于此模型加上影响力传播权重算法,指出度量用户间影响力对商品营销和推广具有重要作用.赵良杰等运用微观扩散模型仿真分析消费者交互作用对网络效应产品扩散的影响[17].
除了考虑微观个体,网络结构的差异也被证明可以促进或者阻碍创新在这个社会中的扩散.真实社会网络呈现Barabási-Albert 网络的无标度特性和Watts-Strogatz 小世界特性,其特征结构显著影响新产品在整个网络中的扩散[18−20].高聚类网络具有很多的冗余连接拓扑结构,Centola 等发现行为在高聚类的网络上传播速度更快,与社交产品的内秉社交属性仍然有所区别,也未发现其增长瓶颈[21].Delre 等[22]以小世界网络为背景,发现最优的目标市场选择策略是选择多个相互分散、高度聚类的小型消费者群体.赵保国等[23]认为网络效应的存在不仅改变了传统扩散模式,而且对个体采纳行为有重要影响,进而指出直接网络效应和间接网络效应对竞争性产品扩散具有阶段性影响.赵正龙等[24]基于个体的差异化选择特征角度,分析了复杂社会网络上的扩散过程及其影响因素, 有助于企业有效管理和控制具有差异化选择特征的扩散.Peres等[25]对比分析了不同网络结构对创新扩散生命周期的影响效应,并指出消费者网络是诸多环境和关系(如网络外部性、消费者口碑、社会信号等)叠加作用的结果.杜宾[26]根据社会学习的主体认知过程和消费者网络结构的线上线下差异性,探索多层次网络叠加条件下的扩散规律.孙耀吾等[27]基于小世界网络研究企业联盟知识扩散特征,发现集聚系数增加和特征路径长度减少可以加快扩散效应.
有学者开始从网络视角出发,结合传染病模型来研究创新扩散的问题.Choi 等[28]构建了基于SIS 传染病模型的平均场扩散过程,利用随机占优理论分析了网络平均度、度分布异质性以及“邻居效应”对扩散的影响.病毒传播模型为创新扩散的研究提供新的研究视角和方法,从而使得基于复杂网络的计算机仿真的研究动态演化成为可能,仿真过程也更贴近现实网络的创新扩散过程.
随着研究的深入,有部分学者开始关注种子顾客对于初期创新扩散以及创新在整个网络中的扩散的重要作用,并且更多从影响力的角度来研究意见领袖型种子顾客对创新扩散的影响[29],或者通过构建无标度社会网络来研究病毒营销活动,探讨在消费者网络中选择初始影响者的方法[30].研究发现,技术扩散的早期,网络中出现种子顾客或者意见领袖会加速创新在社会网络中的扩散[31].黄敏学等将意见领袖所依存的网络划分为社交网络和消费咨询网络,分析了网络节点的信息创造和网络结构对于网络关系构建以及意见领袖形成的影响[32].Peng 等[33]在研究微博信息的最终流行度时,发现信息传播早期转发者的拓扑结构和最终流行程度有很大相关性,若用户所发信息早期的传播深度较广,则有利于信息在社会网络中的广泛传播.而典型的兴趣社交网络微博的用户转发消息的概率受其邻居中已转发此消息邻居之间形成的连通图的个数的正面影响[34].在实物商品在某企业员工中的扩散模拟中发现,种子用户分布越分散,创新扩散获得市场成功所需要的时间就越短[35].
总之,目前微观层面的研究往往对网络拓扑特征的描述以及社会网络拓扑性质的应用研究,比如说初始条件对扩散影响的相关研究,更多关注初始种子用户影响力对创新扩散的影响,忽略了扩散过程中所选取的种子用户在社交网络的网络分布特征的差异、种子用户之间的连接关系差异,也可能会引起的扩散效率的不同.另外,当前关于种子用户分布对创新扩散的研究方法多为数学模型演绎或用少量节点的网络,而在线社交网络是一种典型的复杂网络,节点数量繁多、结构关系复杂,若脱离现实网络数据的复杂性,将使得其研究成果的可靠性及适用性等方面缺乏实证检验[36].
为尝试回答上述问题,本文利用大规模真实社交网络数据,在微观层面上设计基于阈值模型和基于节点相关性的两个实验,在种子用户的不同网络分布及扩散规则下,采用计算机仿真模拟得到结论.
2 研究假设和主要概念界定
社交应用产品是指以交友为目的,以基于各种兴趣组成的交友社区为组织形式的移动应用.社交应用产品相比其他工具类、生活实用类产品来说,具有网络外部性,社交类产品有内生的扩张需求,用户有主动传播给好友的内生动机,从而增加自身的网络价值.针对此类产品从网络外部性角度考虑,内生的传播动机远远超过其他营销因素,可以一定程度上排除其他因素的干扰.由于社交应用的网络外部性特性,之前关于其他类型新产品的推广策略的研究,可能并不适用于社交产品.
本文专指在线社交网络,原因是当前的在线社交网络已经覆盖绝大多数人口,在网络上的抽样,可以充分表达总体特征.兴趣社交网络则是基于兴趣发生用户间连接的社交网络.基于兴趣的社交网络中,用户主动进行传播扩散也是一个相对比较自然的行为,可以在一定程度上排除其他营销因素的干扰.另外就本课题的研究内容而言,社交类应用天然地在线上传播,因而线下零星的口碑传播可以不做考虑.
本文中的种子用户是指产品自传播之前,社交产品开发商通过各种方式在社交网络中获得的第一批用户,也称为初始感染节点集合(感染源).社交产品扩散则指的是用户发现,下载安装社交应用类产品并向好友传播.社交网络中社交产品的扩散并不完全等同于用户采纳与传播,然而由于其社交属性和应用的特殊性,用户传播或转发相关信息大多数情况下都是在用户下载安装使用之后,故研究忽略转发却不采纳的情况.基于上述细微的不同,研究将在不同场合使用“传播”、“采纳”、“感染”和“扩散”等术语.为简化起见,论文认为社交网络中社交类产品的扩散过程就是类似于病毒的传播过程,即社交网络中的节点(即用户)存在已感染(已采纳的用户)和未感染(潜在采纳用户)两种状态.
根据文献[21,34,35]的分析,均发现扩散效率与网络结构或种子顾客在社会网络中分布的关系.现实中亦可观察到,社交应用产品本身可以满足用户需求前提下,同样数量的种子用户,在社交网络中的分布越集聚,社交产品扩散的速度越快.因此提出假设
H1: 社交网络中,种子用户的网络紧密度与社交产品扩散速度正相关.
进一步地,若假设H1 为真,那么种子用户分布的集聚程度对创新扩散速度的正向影响又是怎么样? 文献[13]研究了初始采纳者比例(即数量)与创新扩散之间的正相关关系,同时也在实际传播限项中观察到初始已采纳用户比例对于创新扩散速度的影响迅速变小,即
H2: 社交网络中,种子用户的网络紧密度对社交产品扩散速度的正向影响加速递减.
设社交网络为G=(V,E),其中V 为节点集合,E 为边的集合,初始种群所组成的网络记为G0(V0,E0),那么有G0(V0,E0)⊂G(V,E),则G0的紧密度为

其中L 代表网络中实际存在的边的数量,N 代表网络中种子用户节点的数量.
网络紧密度c 取值范围在0 和1 之间,作为衡量种子用户分布的集聚程度的指标,可以表征种子用户的网络紧密度越大,网络分布越集聚.为表述方便,令

其中x,y 为正整数,x 代表每个小团体中节点的个数,y 代表彼此不直接相连的小团体个数,易知N =xy(见图1 各子图).
在实验中考察社交产品扩散速度,主要观察从种子用户群(时钟0)至整个目标用户群的20%(时钟t)所需要的时长作为扩散快慢的标志.假设H1可量化为,随着种子用户紧密度的增大,创新扩散至整个目标用户群的20%左右所用的时间(达到创新累积采纳百分比20%,即创新扩散“起飞”所用的时间)越短.假设H2量化为,种子用户的不同网络紧密度下,社交产品扩散至整个目标用户群的20%所用的时间间隔越来越短,呈加速递减趋势.
3 仿真实验
为了检验本文假设,使用典型社交网络为基础数据,选取不同数量的种子用户,并在种子用户的不同分布下进行基于阈值模型的仿真实验和基于节点相关性的仿真模拟实验.基于阈值模型的仿真实验考虑初始种子用户的网络分布以及扩散中信息的累积效应对社交产品扩散的影响,重复实验,进而从数据集中观察平均值、中位数、方差和偏度等指标,从而得到高信度的结论.基于节点相关性的扩散仿真实验与基于阈值模型的扩散仿真实验的主要区别在于传播规则需要更进一步考虑已感染节点与未感染节点之间的相关性,进而有倾向地选择邻居节点进行感染.
3.1 社交网络数据获取与分析
本文选取豆瓣网作为仿真实验的样本社交网络.原因是豆瓣网运营多年,覆盖人群非常广泛并比较稳定,可以排除高速增长期或衰弱期平台带来的影响;使用Python 语言编写网页抓取及解析程序,递归地获取社交网络数据.具体步骤为,首先在网络中随机抽取一个用户作为起始用户,获取起始用户关注的对象,进而迭代地对关注的对象进行同样的操作,直到获得足够的数据(代码略).然后利用R 语言和程序包igraph 构建一个无向无权的社交网络图(代码略)并分析.
抓取到的豆瓣社交子网络包含206 891 个节点,544 748 条边,网络紧密度为1.27×105,各节点的度值及其关注的节点的度值表现出显著的异质性,且各用户被其他人关注的差异较大.采用常规社会网络分析方法可得该网络的聚类系数为0.075,最大强连通图的平均最短路径为3.18,即具有一般社会网络的短平均最短路径长度和高内聚的小世界特性,适合作为用于社交产品扩散仿真的社交网络[18].
3.2 基于阈值的仿真实验
为简化工作,社交网络中的节点(即用户)只存在两种状态——已感染节点(代表已采纳的用户)和未感染节点(代表潜在采纳用户),种子用户作为感染源,构成初始感染节点集合;其余用户构成未感染节点集合,感染节点对未感染节点具有持续的传染能力,直至该节点被感染.此外,由于社交类产品的社交属性所蕴含的内生传播动机,用户转发或下载安装试用的过程中均伴随着信息再次传播,因此可以认为未感染节点被感染后会主动向其他未感染节点传播相关信息,从而整个感染过程会主动进行下去,直至网络大部分节点被感染.
实验采用线性阈值模型,感染刺激是指未感染节点接收到一次已感染节点的感染信息.经过初步试算,刺激阈值的大小不会影响实验的结果.因此设定如下感染规则:每个未感染节点累积受到来自相同或者不同易感染节点的感染刺激次数δ ≥10,则该节点被感染.为控制其他因素对创新扩散过程的影响,随机选取种子用户,并大量重复实验过程,从而排除异质性的干扰.算法流程如下:
步骤1初始化种子用户群数量N, 每个子团体的用户数量x, 种子用户群子团体数量y, 迭代次数recursions(default=100);
步骤2加载网络,G0←network.seed-users(N,x,y)生成种子用户群G0;
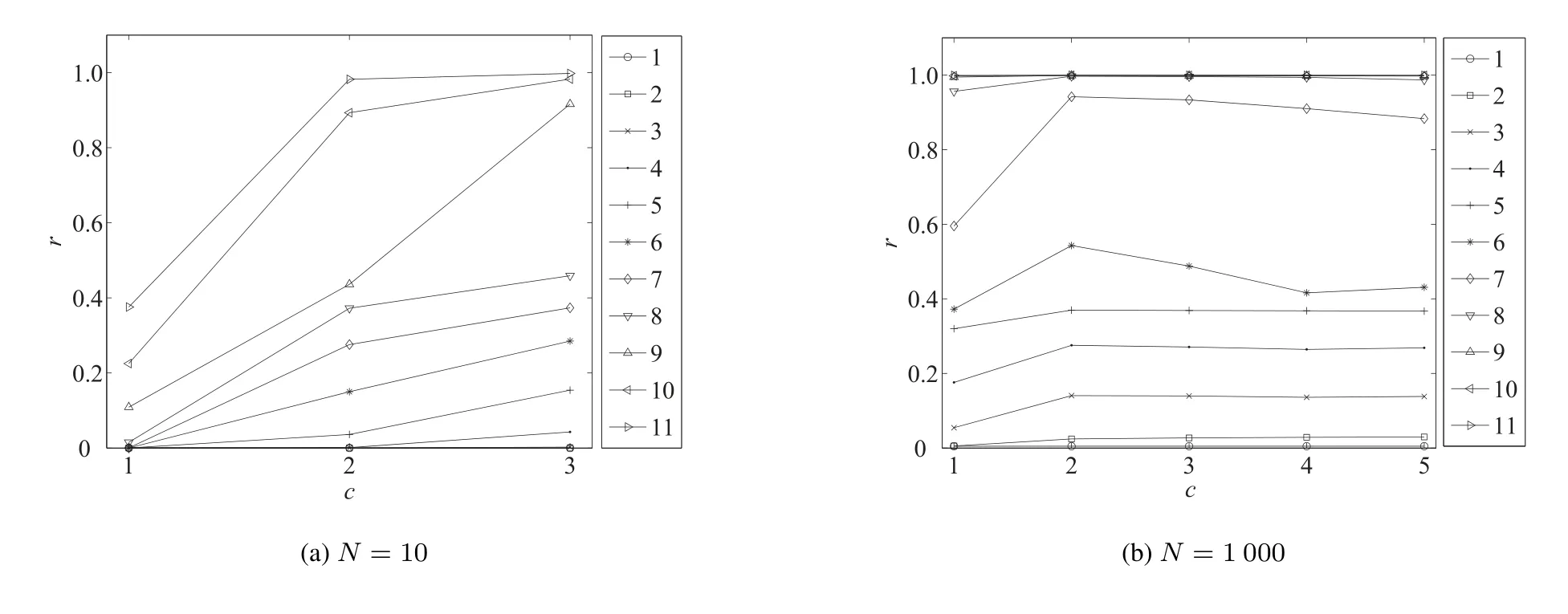
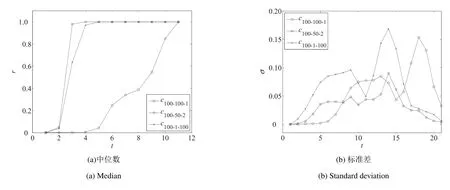
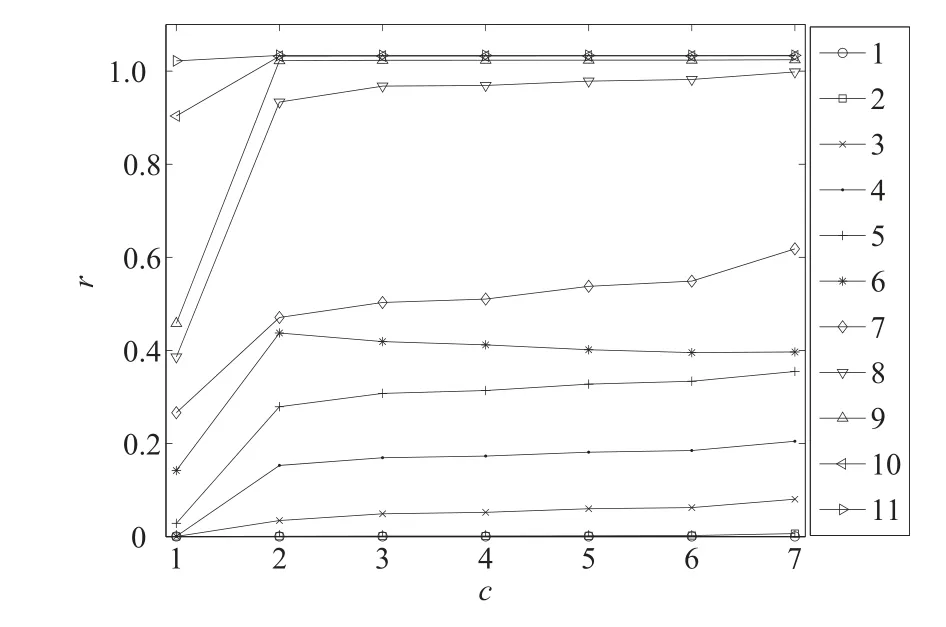
步骤3当r 步骤4获取v 的邻居节点n ←neighbors(v); 步骤5对每个邻居节点进行感染,即n.infected ←n.infected+1; 步骤6若节点v 的受感染超过阈值,即v.infected ≥δ,则将v 加入子图G0←G0+v; 步骤7重复步骤3~步骤6. 实验假定任意一个感染节点阈值都是相同的, 先考察N = 100, (y,x)元组分别为(100,1), (50,2),(25,4), (20,5), (10,10), (1,100), 即c100−100−1, c100−20−5, c100−10−10, c100−20−5, c100−1−100.为提高实验结果的信度, 考察初始种子用户数量规模为N = 10 和N = 1 000 下, 种子用户的网络紧密度对初期扩散速度的影响.鉴于N = 100 实验结果中N 是扩散发生变化的临界值, 当N = 10 时只需分别考察c10−10−1, c10−5−2, c10−1−10三种情况, 当N = 1 000 时只需分别考察c1000−1000−1, c1000−500−2,c1000−250−4,c1000−50−20,c1000−1−1000五种情况.其他创新扩散仿真实验规则步骤和参数均与N =100 实验相同. 1)种子用户的节点数量为10 个时, 上述3 种网络紧密度情况下, 基于阈值模型的创新扩散仿真实验的20 次迭代,100 次重复实验结果如图2 所示. 由于创新累积采纳数量到达目标用户群的20%作为初期阶段扩散取得成功的标志,因此实验结果重点分析初期阶段创新扩散情况.由标准差曲线可以看出,重复实验结果的总体上离差较小.随着种子用户的网络分布紧密度的增大,扩散至20%所用的时间越短,即扩散速度越快,初步验证假设H1 为真(考虑到篇幅,仅给出较能反映数据特征的中位数和标准差指标).由图2 中100 次重复试验的平均值和中位数扩散曲线可以看出,扩散曲线c10−10−1和c10−5−2间距较大,而c10−5−2和c10−1−10间距突然变小,即当种子用户的网络分布紧密度为0(即c10−10−1)的基础上小幅度的提高,扩散速度便有了极大的提高,随着紧密度继续增大,其对扩散速度增长的影响变小,初步验证了假设H2 为真. 2)种子用户数量为100 时,其不同网络分布紧密度下的20 次迭代,100 次重复试验的结果如图3 所示.由图3 可以看出,初始种子用户数量为100 时,其不同网络分布紧密度下的100 次重复实验结果的标准差曲线和偏度曲线总体上离差较小.从整体趋势上看,节点数量为100 的种子用户的不同网络紧密度下,100 次重复试验的平均值和中位数扩散曲线陡峭程度大体一致.随着种子用户的网络分布紧密度的增大,创新扩散至20%所用的时间越短;从整个扩散过程来看,种子用户的网络紧密度越大,创新扩散到达峰值的时间也越早,同样初步验证了假设H1 为真. 图2 种子用户的不同分布下基于阈值模型的仿真实验结果(N =10)Fig.2 The results of simulation experiments based on threshold model under different distribution of seed users(N =10) 由图3 中100 次重复试验的中位数扩散曲线可以看出,扩散曲线c100−100−1的启动时间远远滞后于介于c100−50−2和c100−1−100的之间时的扩散启动时间,而介于c100−50−2和c100−1−100之间的扩散启动时间差异骤然变小(扩散曲线几乎重合).可见,当种子用户的网络分布紧密度在0 的基础上小幅度提高,其扩散速度便有了极大的提高,而随着紧密度继续增大,其对扩散速度的增长的影响加速变小,初步验证了假设H2为真. 图3 种子用户的不同分布下基于阈值模型的仿真实验结果对比分析图(N =100)Fig.3 Comparison and analysis diagram of simulation experiment results based on threshold model under different distribution of seed users(N =100) 3)种子用户的节点数量为1 000 个时,其5 种紧密度情况下的20 次迭代,100 次重复仿真实验结果对比分析图如图4 所示. 由图4 可以看出,种子用户节点数量为1 000 时,其不同网络紧密度分布下,感染节点数量的增长极其迅速.从开始感染到覆盖整个网络,仅经历了15 次左右的迭代过程.从扩散曲线的整体趋势上看,节点数量为1 000 的种子用户网络紧密度越大,创新扩散至目标用户网络的20%所用的时间越短,或到达峰值的时间也越早.进一步验证了假设H1 为真.同样可以看出,当种子用户的网络分布紧密度在0 的基础上小幅度的提高,其扩散速度便有了较大的提高,当种子用户的网络分布紧密度继续增大时,其对扩散速度的增长的影响骤然变小,验证了假设H2 为真. 图4 种子用户的不同分布下基于阈值模型的仿真实验结果对比分析图(N =1 000)Fig.4 Comparison and analysis diagram of simulation experiment results based on threshold model under different distribution of seed users(N =1 000) 图5 为不同时刻下,节点数量为10 的种子用户的创新累积采纳百分比随其网络紧密度的变化而变化的轨迹图. 图5 不同时刻下,累积采纳百分比随种子用户紧密度变化而变化曲线(N =10,1 000)Fig.5 The change curve of cumulative adoption percentage with the change of seed user tightness at different times(N =10,N =1 000) 可以看出,初期扩散取得成功时(扩散至整个目标网络的20%用户),即t=18 时刻下,轨迹曲线图在临界紧密度c10−5−2前后变化存在显著差异.在临界紧密度之前,曲线非常陡峭,在临界紧密度后,曲线骤然变缓,几乎呈水平线.节点数量N = 100 实验中在t = 7 时刻下,轨迹曲线图在临界紧密度c1000−500−2前后变化存在显著差异.在节点数量N =10 实验中,类似情况出现在t=13 时刻临界紧密度为c100−50−2时. 因此,初始种群节点数量规模为10,100 和1 000 实验的共同结论是当种子用户的网络紧密度在0的基础上有小幅度提升时,创新扩散的速度迅速得到提升.然而,紧密度提升到1的过程中,种子用户的网络紧密度对创新扩散速度的正向影响呈加速式递减,假设H2 为真. 选取不同节点数量的种子用户(10,100 和1 000)进行仿真实验对比分析发现,扩散的初始阶段,扩散速度最慢的为c10−10−1,扩散速度最快的为c1000−1−1000(与c1000−500−2几乎重叠,如图6).这一方面说明初始传播阶段,由于初始种群的数量规模相差较大(100 倍),种子用户群的数量越大,扩散的速度越快,这也比较符合现实情况. 另外一个有趣的现象是,c10−1−10扩散至整个网络的20%所用时间比c100−100−1要短,同样c100−1−100扩散至整个网络的20%所用时间比c1000−1000−1的时间短.显然在一定节点数量范围内,种子用户的较为集聚,能够弥补其数量方面劣势,种子用户的网络紧密度对扩散速度的正向影响更为显著. 基于阈值模型的仿真实验只考虑初始种子用户的网络分布以及扩散中信息的累积效应对社交产品扩散的影响,没有考虑社交网络中用户之间的相关性,即一个用户对另一个用户的创新采纳决策影响力.在现实的社交网络中,当社会网络结构确定时,社交产品是通过节点(用户)间的相互连接来进行扩散的,不同节点之间相互影响力是不同的,而节点的影响力在一定程度上表现为节点vi的度数ki和与之相连的节点vj各自的度kj之间相关性,相关性越强,节点vi对节点vj的行为影响力越大.因此,在这种情况下,潜在采用者个体(即未感染节点)形成的网络实际上是一个由节点之间的相关性形成的权重网络.因此,出于完备性的目的,本文进一步设计了基于节点之间的相关性(影响力)的扩散仿真实验来考察初始种子用户的网络分布对社交产品扩散的影响. 基于节点相关性的仿真实验的种子用户选取根据上述网络紧密度模型构建规则以及网络分布模型图的具体构建思路,以及基于阈值模型的仿真实验结果,选取c100−100−1,c100−50−2,和c100−1−100各3 种不同网络紧密度分布进行实验. 未感染节点在决策是否采纳某项新产品时,会优先考虑它的邻居中那些已感染的意见领袖或者“明星节点”的建议.但同时,如果未感染节点的邻居非常少,即使这些邻居只是普通节点(即度值比较小),也会对未感染节点产生比较大的影响,因为由于邻居数比较少增大了未感染节点看到已感染节点传播的信息的概率,进而也会使增大该节点被感染的概率. 设节点i 的度数为ki,节点j 的度数为kj,i,j 直接相连,则节点j 对i 的相关性为 基于节点相关性的扩散仿真实验的感染规则:首先计算所有已感染节点和它的邻居未感染节点之间的相关性,将该相关值作为刺激值,根据其数值从大到小排列,未感染节点受到相同或者不同节点的感染刺激阈值δ ≥10. 仿真实验结果分析100 次重复实验结果如图6 所示, 种子用户的网络紧密度越大, 创新扩散曲线越陡峭; 无论是平均值还是中位数的扩散曲线都可以看出, c100−50−2和c100−1−100扩散至整个网络的20%(约40 000 个节点)所用的时间均远小于c100−100−1时所用的时间,即种子用户的网络紧密度越大,创新扩散的速度越快.其中c100−50−2和c100−1−100下速度虽然相差不大,但是c100−50−2的扩散速度要大于c100−1−100的扩散速度,说明基于节点之间相关性的扩散规则下,种子用户的网络分布集聚状态下的扩散速度均比分散状态下的要好,但是超过一定临界值后敏感性减弱,因此,在实际的应用中,需要根据节点的数量选择适当紧密度的种子用户进行社交产品的扩散.由此验证假设H1 为真. 图6 种子用户的不同分布下基于阈值模型的仿真实验结果(N =10,100,1 000)Fig.6 Threshold model based simulation result on different seed user distribution(N =10,100,1 000) N =100 时的种子用户的不同分布下基于节点相关性的仿真实验结果如图7 所示.由图7 的不同时刻的平均值和中位数扩散曲线可以看出,初始种群的节点数量为100 时,随着其紧密度的增大,社交产品的扩散速度的增大幅度先增大大过了临界值后减慢,即初始种群紧密度对于扩散速度正向影响是加速递减的,验证了假设H2 为真. 图7 种子用户的不同分布下基于节点相关性的仿真实验结果(N =100)Fig.7 Node correlation based simulation result on different seed user distribution(N =100) 图8 为不同时刻下,节点数量为100 的种子用户群的创新累积采纳百分比随其网络紧密度的变化轨迹.可以看出在t=13 时刻下,随着种子用户网络紧密度的增大,创新累积采纳百分比先加速爬升,然后骤然变缓,临界紧密度均为c100−50−2,当种子用户的网络紧密度由c100−100−1增大到c100−50−2时,创新累积采纳百分比有很大幅度的提升,而当种子用户的网络紧密度由c100−50−2继续增大到c100−1−100的过程中,创新累积采纳百分比增大幅度差异极小.可见,种子用户节点数量规模为100 情况下,种子用户网络分布紧密度对创新扩散速度的提升作用并非都是显著的,当种子用户的网络紧密度在0 的基础上有小幅度提升时,创新扩散的速度迅速得到提升,然而,当种子用户的网络紧密度进一步提升到1 的过程中,种子用户紧密度对创新扩散速度的影响几乎很小,种子用户的网络紧密度对创新扩散速度的正向影响加速递减,进一步验证了假设H2 为真. 图8 基于阈值实验,不同时刻下,累积采纳百分比随种子用户紧密度变化曲线(N =100)Fig.8 Based on the threshold experiment,the change curve of cumulative adoption percentage with seed user tightness at different time points(N =100) 图9 为基于节点相关度实验, 也有同样结论.与节点数量为100 的基于阈值实验相比, 不同在于时刻t = 9,临界紧密度c100−5−2前后出现显著差异.显然,找感兴趣的人进行传播,效率更高,这也与人们生活实践中的思维习惯一致. 图9 基于节点相关度实验,不同时刻下,创新累积采纳百分比随种子用户紧密度变化的曲线(N =100)Fig.9 Based on the node correlation experiment,the curve of cumulative adoption percentage of innovation as a function of seed user tightness at different time points(N =100) 本文基于大规模兴趣社交网络,选取不同数量的种子用户,利用基于不同的扩散规则结合已有的步进累积研究方法,验证了种子用户紧密程度与扩散效率的正相关关系.论文的贡献在于从微观角度出发,研究扩散过程的影响因素,同时利用大规模真实社会网络数据进行仿真,使研究在实际社交网络中得到高信度的验证.论文同时还发现了紧密度的贡献存在瓶颈,其现实解释为,紧密度是推动初期扩散的主要因素,但到了一定阈值之后作用被其他潜在因素替代,这也是未来需要进一步探讨的问题. 在营销实践中,选取的种子用户符合集聚网络的分布特征时,反而会比分散“撒网”策略更有利于新产品的扩散.论文的结论有助于企业在有限的营销预算下,选取适合的种子用户网络分布策略,有效地投放营销资源,提高产品传播能力和采纳率,带来更大经济和社会效益.此外,鉴于种子用户的网络紧密度超过一定的临界值后,其紧密度对创新扩散速度的提升幅度呈加速减小趋势,因此需要根据企业的实际情况以及预期扩散效果和扩散数量,选择合适集聚程度的种子用户分布进行新产品的推广.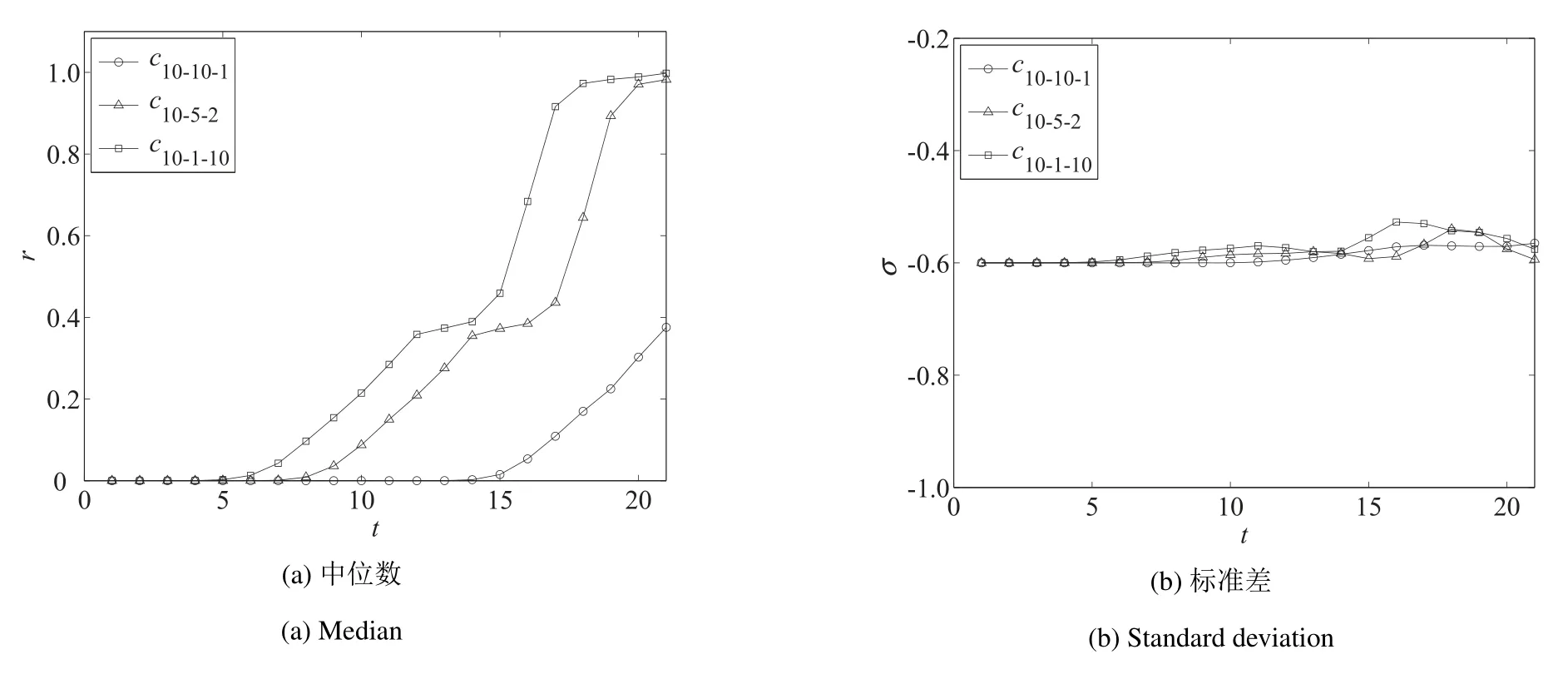
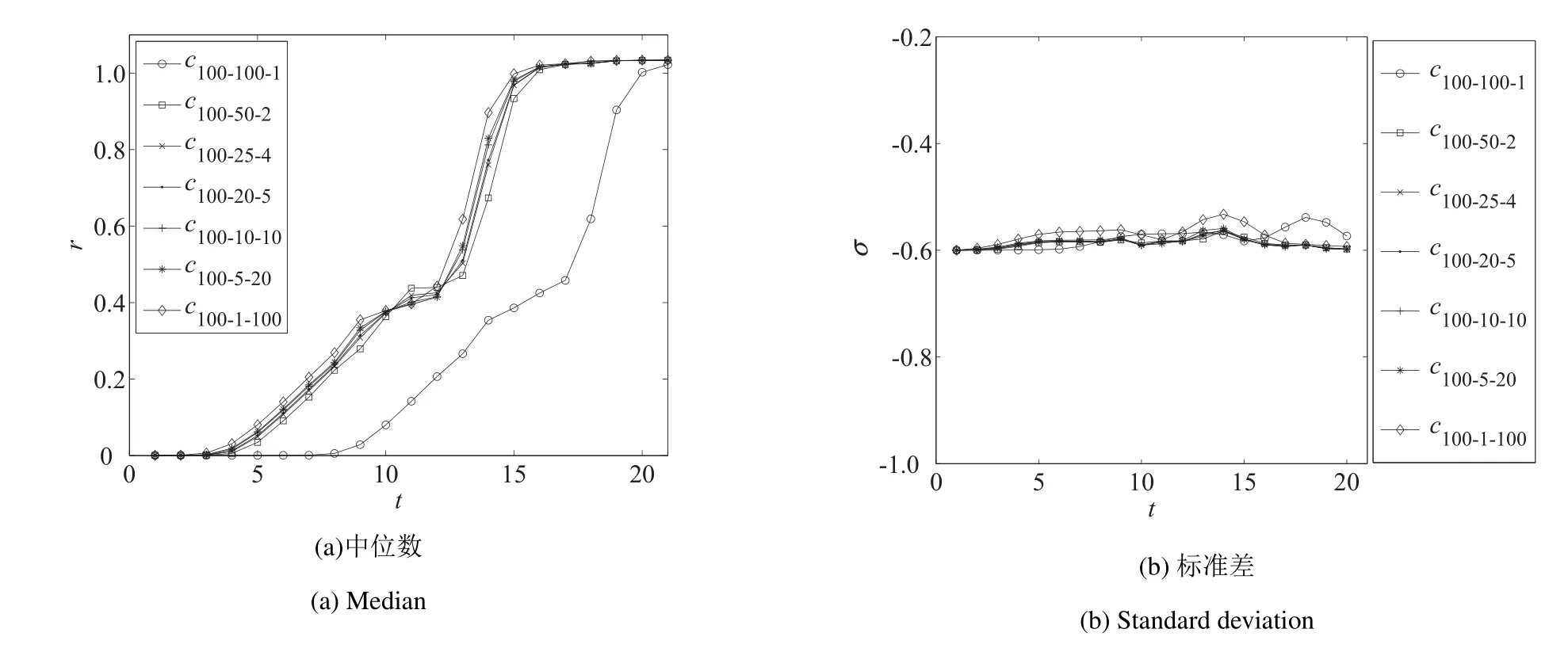
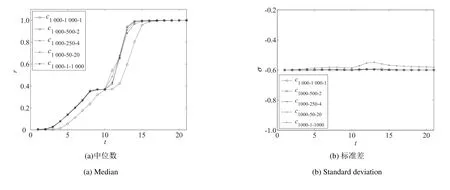
3.3 基于阈值模型的仿真实验结果对比分析
3.4 基于节点相关性的仿真实验



4 结束语

