库存容量有限的产品选择及联合采购决策研究

石雪飞, 王海燕

(东南大学经济管理学院,江苏南京211189)

1 引 言

随着经济和科技的发展,商品种类和数量越来越多.面对市场上种类繁多的产品,百货商店,超市等零售商由于资金和库存容量的限制,很难购进所有品牌和型号的产品,需要选择收益高的产品销售.在选择产品时,有的产品销量好,但体积大,利润低.有的产品销量不是很好,但利润却很高.在库存容量限制下如何做出最优的选择?实际上,很多零售商选购产品时更多的是依靠主观上的经验.

在学术领域,学者们更热衷于研究供应商的选择问题[1−3],仅有少量文献研究产品的选择问题[4],其中主要以普通产品和升级产品的选择决策[5,6]为主.供应商选择问题则是制造商或零售商们考虑产品质量,供货能力,供应商信誉,采购成本和售后服务等因素,从而选择出最有利的供应商.大部分供应商选择的定量分析的文献中,以最小化总成本为目标[7−9],而选择产品时,零售商们通常优先选择收益高的产品.选对了供应商不意味着选对了产品.不同的产品售价和成本往往都不一样,因此选择成本小的产品可能不是最优的选择,故供应商选择的研究并不适用于产品的选择问题.

生产企业常用最小订货量来确定最优的生产计划[10,11],许多供应商要求采购企业的订单至少要达到其最小订货量.但个性化的消费使得消费者对单一产品的依赖程度越来越低,导致了越来越多的小批量订货.规模小的零售商最优订货量可能达不到供应商的最小订货量要求,按照最小订货量订购产品会增加零售商的库存成本.故本文将最小订货量作为产品选择模型的一个约束条件.实际上,库存容量限制和最小订货量限制是库存补货决策模型中很普遍的约束条件,如文献[12–15]等.

最小订货量的限制以及小批量采购的高成本导致了越来越多的联合采购.联合采购通常是将小批量的订单形成一个大订单进行采购,这样能够形成规模经济效应,减小采购成本[16].显然联合采购能够更容易满足供应商的最小订货量的要求.然而,采购周期的协调是联合采购的一个困难.单独采购时一旦发现库存水平低于订货点就可以立即采购.联合采购时需要合作成员的需求量积累到一定的量或者等到约定的采购时间才会进行采购.采购之前有的成员库存提前销售完,在等待采购的过程中造成缺货损失.若联盟成员都愿意共享库存那么就会降低缺货损失.并且库存共享能够降低库存成本,减少运营成本,改善服务水平[17].因此本文考虑共享库存的情况下进行联合采购.

联合采购问题的另外一个难点是分配问题,如何分摊费用或分配利润是联合采购联盟达成的的关键.不公平的分配机制会导致联盟成员退出合作联盟[18].许多学者致力于研究联合采购的成本/利润分摊机制,Schotanus 等[19]调查发现87%的合作联盟采用等价法分配收益,而13%的联盟采用利于规模大的成员的分配方案.冯海荣等[20]研究了非瞬时补货情况下易腐品联合采购的分配问题,并给出了一个核分配方案.肖旦等[21]研究了产品中含有残次品情况下的联合采购模型.Heuvel 等[22]针对零售商多阶段联合补货问题,建立了ELS(Eonomic lot sizing)博弈模型并证明了其核为非空的.可以看到这些文献都应用合作博弈理论寻找核分配方案.这是因为核分配方案能够促进联合采购成员形成稳定的合作联盟,它能保证参与合作的成员收益最大化.但核分配方案并不总是存在的或容易找到的,不同合作环境下的核分配方案或接近核分配方案的近似核分配方案需要学者们去探索.

零售商选择供应商时通常是选择信用最好成本最低的供应商,而选择产品时则会选择利润最高的产品.以前的文献主要以供应商选择为主,仅有少量文献研究两种产品的选择,而目前并没有文献研究库存容量和最小订货量约束下多产品的选择和采购决策.故本文构建了库存容量和最小订货量约束下的单独采购时产品选择和采购量决策模型.为进一步帮助零售商提高利润,建立了库存共享条件下的联合采购模型.分别设计了多项式时间算法来求解这两个模型.分配是合作的关键,因此,本文基于合作博弈利理论设计了利润分配方案并证明了在联盟库存容量充足的情况下采用的分配方案是核分配方案而在库存容量不足时采用的分配方案是满足个人理性的并且能够激励零售商共享其真实的库存容量信息的有效分配方案.数值实验结果表明联合采购能够帮助合作联盟提高26%的利润.

2 单独采购决策模型

假设:

1)零售商位于同一区域,不同零售商都以供应商建议的统一零售价销售产品.

2)采购是瞬间完成的,没有等待时间,即交货期为0.

3)供应商已确定,采购成本参数已知.

本节研究零售商单独采购时零售商决策是否选择采购产品以及产品的采购量.各产品的采购是独自完成的,采用的是连续采购策略,即当库存不够时立即补货.下面是本文主要参数和假设: 某一区域有m个零售商,市场上有n个不同品牌的产品,由不同的供应商供应,记M={1,2,...,m},N={1,2,...,n}.供应商要求产品i,i ∈N需要达到的最小订货量记为产品i的体积为vi,产品i的固定采购费用为ki,采购价格为ci,零售价为pi.零售商j,j ∈M销售产品i,i ∈N单位时间的需求到达率为λji,单位时间单位体积的库存成本为h,零售商j的最大库存容量为Vj.

零售商采用连续库存检查策略, 当产品i的库存为0 时立即采购qji.产品i产生的总成本包括库存成本和订货成本.零售商j的产品i的期望采购周期为qji/λji, 可得到其在一个周期内总成本为若零售商以最大化长期平均期望利润为目标,那么零售商j的优化模型为

其中qji,xji为决策变量,qji是产品i的每个周期的采购量,xji=1 表示采购产品i,xji=0 则表示不采购采购产品i,式(2)为最小订货量约束,式(3)为库存容量约束.

考虑模型(Pj)中的一个特殊情况,即

在此情况下只要产品i被采购,其最优采购量为是一个确定值,只需决策xji.而此时通过模型(Pj)求解决策变量xji为一个经典的二维背包问题,其中λjivi为物品体积,是为物品单位体积的价值,而Vj为背包的容量并且背包容量是不足的.

0-1 背包问题是NP–难的,目前仍然没有证明存在多项式时间算法求得该问题的最优解.模型(Pj)中的一个特殊情况时已经是一个NP–难问题,为此,设计了多项式时间内可解的启发式算法来求解一般情境下的模型(Pj),证明在一定条件下可求得最优解.

求解模型(Pj)的算法(记作算法1)步骤如下:

步骤1输入参数值λji,pi,qmini ,ki,ci,h,vi,Vj,i ∈N;

步骤2

步骤3

步骤4找出{fl}l∈S中最大的值

步骤5如果fi′ >0 且

步骤6将S中i′删除和更新剩余的库存容量即

步骤7如果S=∅或Vj=0 或fi≤0,i ∈S,那么终止算法;否则回到步骤2;

步骤8输出结果

定理1算法1 是多项式时间算法,其时间复杂度为O(n2),并且当下列情况之一成立时算法1 得到的解为模型(Pj)的最优解:

1)库存容量充足.

3)存在常数b,有λjivi=b,i ∈N.

证明首先证明算法1 是多项式时间算法.在算法1 中, 对于每个零售商, 找出第一个购进的产品需要计算n次qji和fi, 找出第二个购进的产品需要计算n −1 次, 以此类推,总共要计算不多于n+(n −1)+···+1 =n(n −1)/2 次,而qji,fi的计算量是一个常数,因此算法1 的计算时间复杂度为O(n2).

然后证明三种情况下,算法1 的解是模型(Pj)的最优解.

情况1库存容量充足.在此情况下式(3)的约束可以忽略掉,然后模型(Pj)可以分解成如下n个子模型

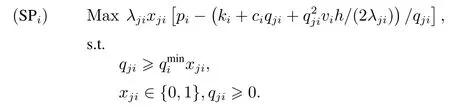
情况2存在常数a使得(piqji −(ki+ciqji+(2λji)))(qjivi)−1=a,其中λji(pi −(ki+ciqji+(2λji))是产品i的总利润,[piqji −(ki+ciqji+(2λji))](qjivi)−1是产品i单位体积的价值.

那么这个问题可以转变成一维背包问题,λjivi是产品体积,Vj是背包容量,单位体积的产品价值是一样的.一种产品可以看成一个物品,每个物品的单位体积的价值是一样的,物品i的总价值为fi=λjivia,其中λjivi为物品的体积.那么背包里物品所占空间越大,背包里的价值越高.而算法1 是先选择价值高的物品,也就是陆续将物品按体积从大到小装进背包里,这样背包装的就是价值最高的.因此,算法1 得到的是最优解.

情况3存在常数b,有λjivi=b,i ∈N.这种情况下同样把这个问题转化成一维背包问题,其中物品的体积为λjivi,物品的价值为fi.而物品的体积λjivi都是一样的,对于固定的背包容量Vj,最优的装包方案是先装价值高的物品.fi计算的正是产品i的总利润即物品的价值,fi越大,物品的价值就越高,因此算法1 的解是最优解. 证毕.

定理1 证明了算法1 是一个多项式时间算法,这也意味着当产品种类较多的时候,算法1 也能够快速求解模型(Pj),但算法1 并不能保证得到的解是模型(Pj)的最优解,只有满足定理1 中三个条件的其中一个才是最优解.

3 联合采购决策模型

本节的目的是求出参与联合采购联盟所有成员的采购量和库存目标.假设零售商愿意共享需求和库存容量信息,存在一个可信赖的零售商或者第三方来组织联合采购,组织者需要决策联合采购的补货量,并且联合采购是在单独采购决策之后的,即参与联合采购的零售商的采购的产品种类是确定的,采购量则是需要联合采购决策的.通过第2 节的模型(Pj),零售商们都确定了自己要采购的产品,不妨假设模型(Pj)的最优解为若所有参与联合采购联盟的零售商共享采购周期,即联合采购联盟的零售商采购同一种产品的周期是一样的.下面建立采购联盟的长期平均利润函数来确定联合采购时产品的采购量.零售商j的产品i期望采购量记为为产品i的总采购量.由于采购周期一样,所以也有记合作联盟的产品i的总需求到达率为由于零售商们共享库存,且交货期为0.因此当所有零售商的产品i的库存为0 时,联盟向供应商发出一个联合采购订单量为Qi的订单.那么产品i的期望采购周期为由集合M中成员形成联盟的长期平均总利润模型为

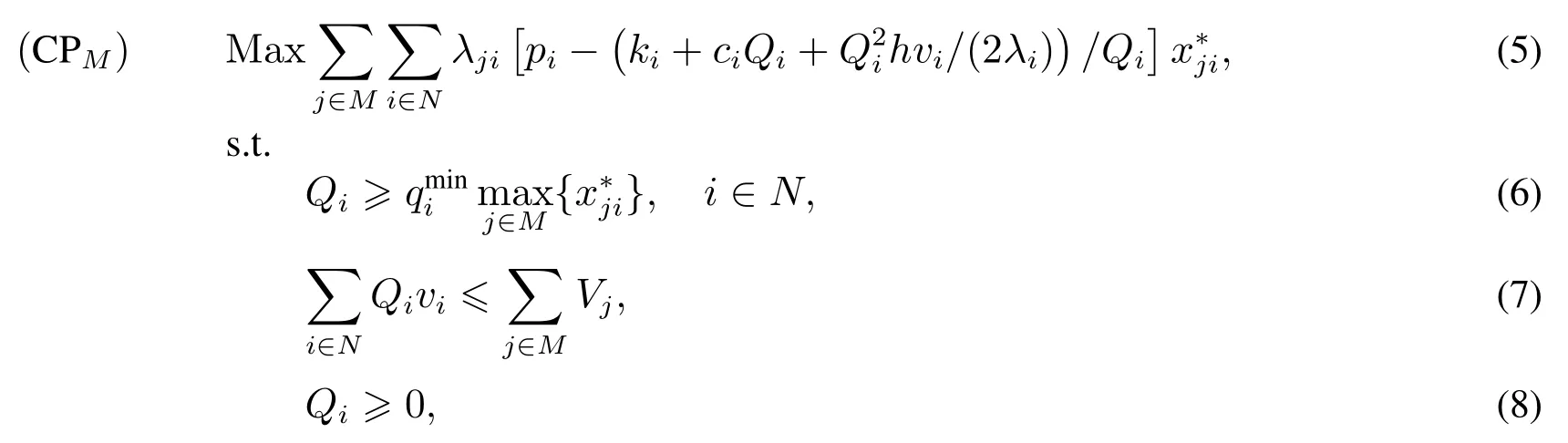
式(5)为最大化联盟的单位时间内的总利润,决策变量为零售商的采购量Qi,式(6)为供应商最小订货量的约束,式(7)保证了零售商有足够的库存容量接收采购量,式(7)中的右边是合作联盟共享库存后的总库容量.

求解模型(CPM)的算法(记作算法2)步骤如下:

步骤1输入参数λji,pi,,ki,ci,h,vi,Vj,,j ∈M,i ∈N;

步骤2计算下面的参数值,

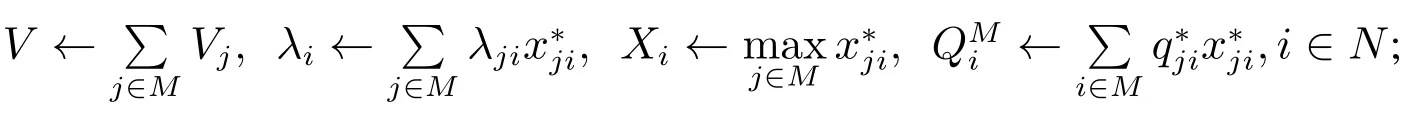
步骤3如果那么进入步骤8,否则进入步骤4;

步骤4∀i ∈S,如果

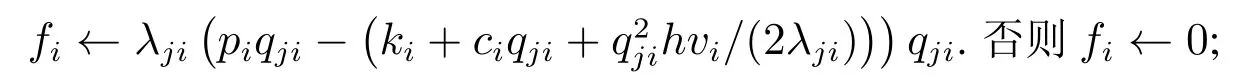
步骤5找出{fl}l∈S中最大的值记为fi′,如果fi′ >0,那么

步骤6将S中i′删除和更新剩余的库存容量即S ←S{i′},V ←V −

步骤7如果S=∅或V=0 或{fi≤0|i ∈S}进入步骤12,否则回到步骤4;

步骤8对于Xi= 1 且如果S′∪{i},否则更新联盟库存容量V,即V ←V −若不满足条件Xi=1 且=0,i ∈N,则进入步骤9;

步骤9

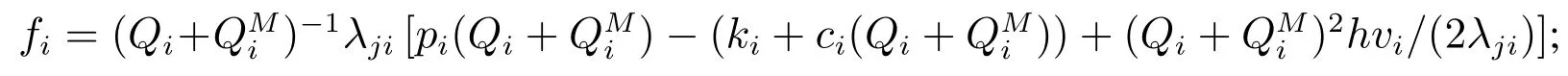
步骤10若fi′为{fl}l∈S′中最大的值,将S′中i′删除和更新剩余的库存容量即S′ ←S′{i′},V ←V −Qi′vi′;

步骤11如果S′=∅或V=0,则进入下一步,否则回到步骤9;

步骤12

步骤13如果Qji > Vj/vi, 那么否则Vj ←Vj −Qjivi,i ∈M,j ∈N;

步骤14从{Vj}j∈M中找出最大的值找出中最大的值如果那么否则

步骤15若q′i=0,i ∈N,则结束算法2,否则回到步骤13;

步骤16输出结果

当库存容量不足时,首先保证每种产品的采购量不低于任何一个零售商单独采购时的采购量,然后将库存容量优先分配给利润高的产品.确定合作联盟的总采购量之后,将联盟的总采购量分配给联盟成员,也就是从算法2 中的步骤11 开始,其计算量为O(nm)+O(nm)+O(n2).因此,算法2 也是多项式时间算法.注意到并不是零售商j每个周期对产品i的需求量,而是每个周期零售商j对产品i的目标库存量.零售商j对产品i的需求量为但由于零售商j的库存空间可能不够,需要存储在其他零售商的库存容量里,从而可能导致

4 利润分配方案设计

信息共享是合作联盟合作的基础,然而一个能让联盟所有成员接受的分配方案是合作的关键.公平合理的分配方案能够促进采购联盟长期稳定的合作,而合作博弈理论是研究合作联盟运作策略和稳定性的理论,因此本节将基于合作博弈理论设计利润分摊方案.

将由集合M中的成员参与合作的博弈定义为(M,ν),其中Π: 2M→R,ν(∅) = 0.同时满足下面条件的利润分配方案为核分配方案或者称这个分配方案是在联合采购博弈的核中的,即

其中是合作联盟M分配给成员j的利润.

满足1)的分配方案称为有效分配方案.把所有成员都参与合作形成的合作联盟称为大联盟.R为M的子集,子联盟R所产生的利润是不大于R中所有零售商从大联盟的所获的利润之和的.故从利润的角度上考虑,子联盟R若是理性的集体则不会脱离大联盟来形成小联盟R的,因为子联盟R无法得到更高的利润.同时可以看到R={j}时,≥ν({j}),这意味着合作之后零售商分配到的利润不会比单独采购所产生的利润低.故从利润的角度上考虑,对于理性的零售商而言是不会采取单独采购的.1)和2)表明核分配方案是满足集体理性和个体理性的有效分配方案,它能保证任何子联盟离开大联盟都不能获得更大收益.因此,核分配方案能够保证理性的零售商都参与合作,因为他们都参与合作能够获得最大的利润.

定义联合采购博弈(M,Π),其中Π是联合采购联盟的总利润,那么合作联盟M的总利润为

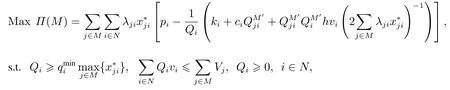
其中剔除了不采购的产品.那么易知Π(M)的最优解和模型CPM的最优解是相同的,Π({j})的最优解和模型(Pj)的最优解是相同的.

引理1联合采购博弈是超可加的.

证明设R,T ⊆M且R ∩T=∅,R ∪T=H,分别是Π(R),Π(T),Π(H)的最优解.记是Π(H)的一个可行解,所以有

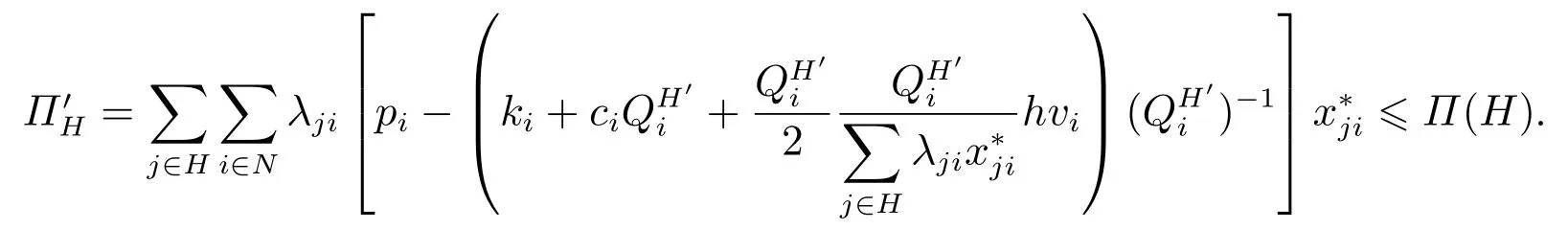
又因为Π′H≥Π(R)+Π(T),所以有Π(R)+Π(T)≤Π(H). 证毕.

超可加博弈是核分配方案存在的必要条件,引理1 表明这个合作博弈的核是有可能找到的.

下面首先给出两种分配方案,记

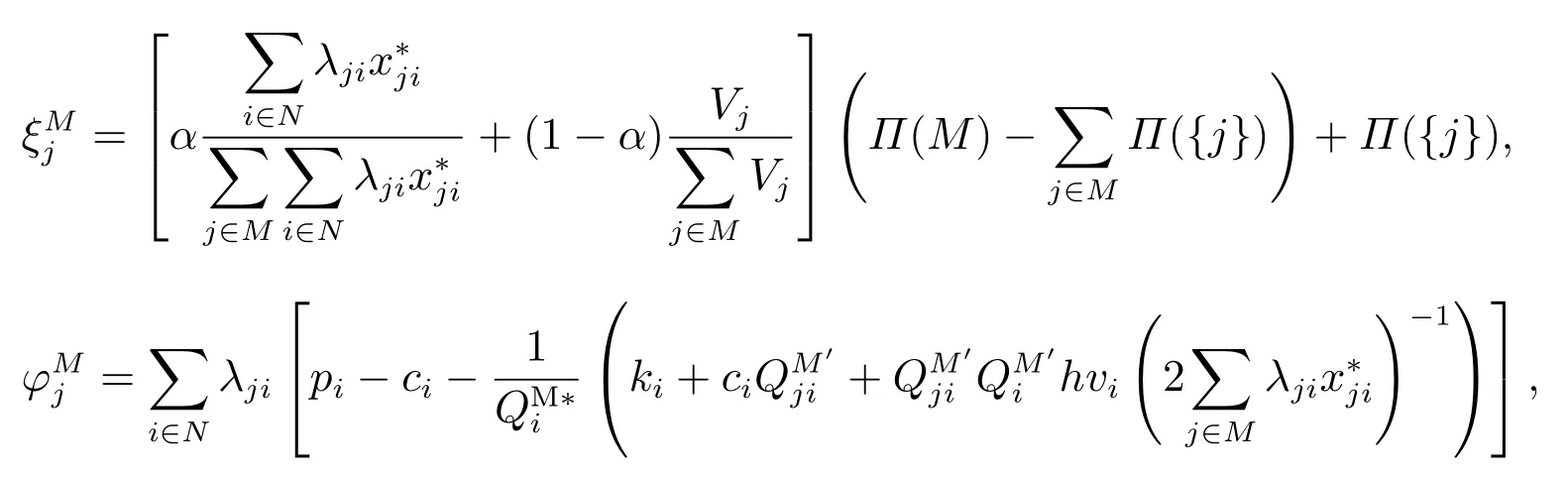
其中分别表示联合采购联盟M分配给零售商j的利润分配方案,是Π(M)优化模型的最优解.

定理2当分配方案φ= (φ1,φ2,...,φm)是联合采购博弈的核分配方案.当分配方案ξ=(ξ1,ξ2,...,ξm)是满足个人理性的有效方案.

证明1)即联合采购联盟的库存容量充足.首先,

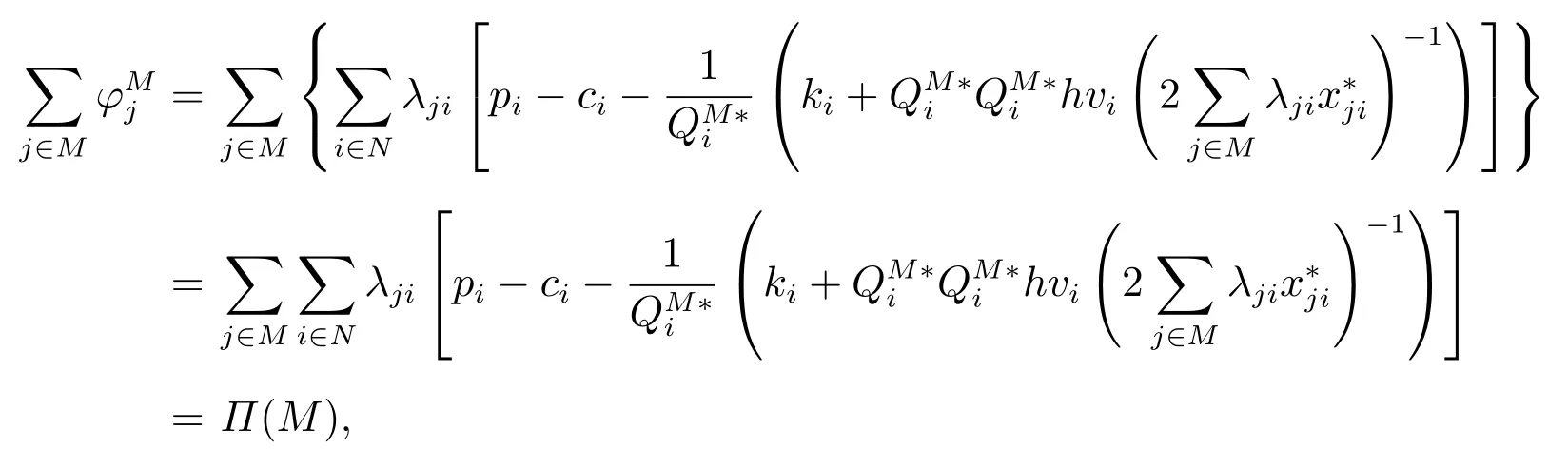
因此,φ=(φ1,φ2,...,φm)是一个有效分配方案.记为Π(R)的最优解,联合采购联盟的库存容量是充足的,产品i的最优订货量为那么

故

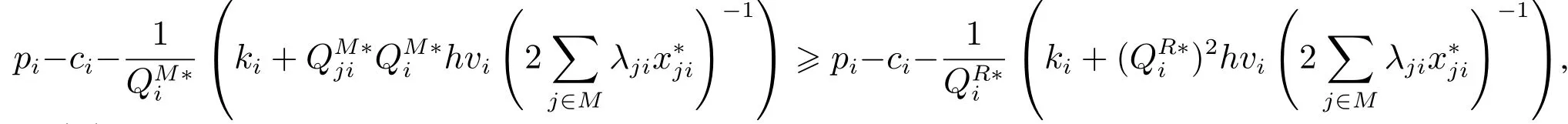
因此有

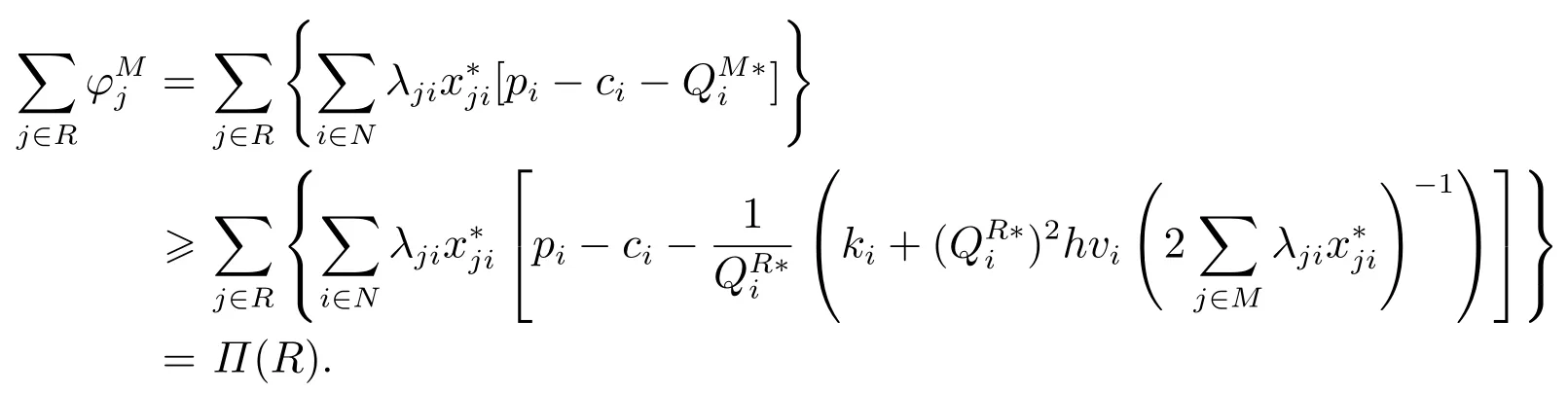
因此,分配方案φ=(φ1,φ2,...,φm)是联合采购博弈的核分配方案.

首先有

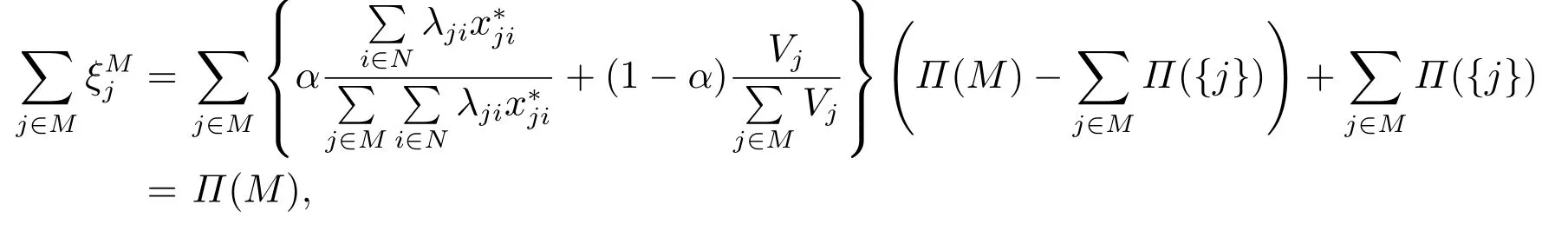
因此,分配方案ξ=(ξ1,ξ2,...,ξm)是有效分配方案方案.

情况I

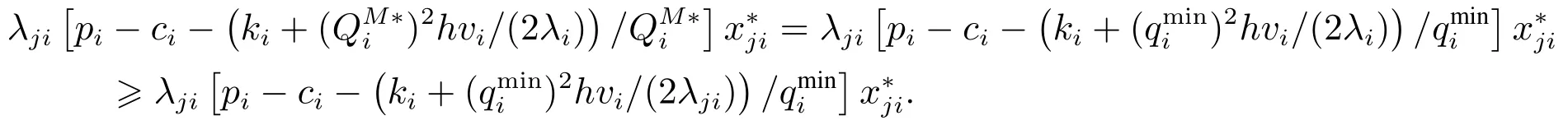
情况II

综合情况I 和情况II,可知

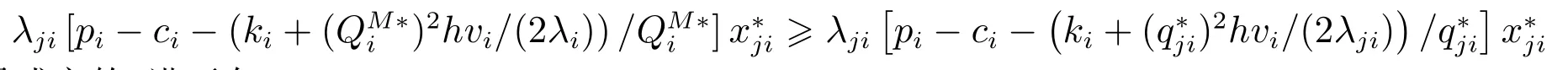
总是成立的.进而有

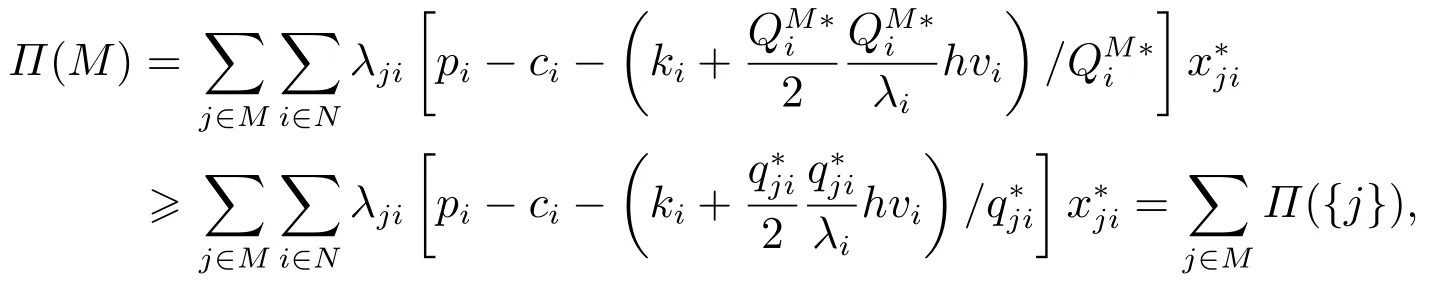
这保证了合作之后分配到的利润不会比单独采购时获得的利润低,说明分配方案ξ= (ξ1,ξ2,...,ξm)是满足个体理性的.因此,分配方案ξ=(ξ1,ξ2,...,ξm)是满足个体理性的有效分配方案. 证毕.

定理中的φj,ξj是库存容量充足和不足的情况下在单位时间内分别获得的收益.这个收益可以表示为销售收入减掉采购成本和存储成本,而销售入和存储成本通常是零售商自己管理的,联合采购联盟只管理采购费用.因此需要计算每次采购的零售商应该支付的采购费用.并且不同产品的采购周期可能不一样,因此,下面计算零售商j在采购产品i时所需支付的费用.值得注意的是若计算结果为证表示零售商向联盟支付的费用,若为负则表示联盟向零售商支付的费用.

φj是联盟库存容量充足的情况下零售商j最终分配到的利润,合作联盟可以通过零售商支付采购成本来达到利润的分配.假设销售的收入归零售商自己所有,库存产生的成本也由零售商自己承担,每次采购联盟收取相应的采购成本.由于库存共享,零售商j的库存量未必是零售商j的需求量.定理2 的分配方式实际上是按照需求比例分摊固定成本,各自承担自己所需采购量的采购成本和存储成本.且算法2 得到的是零售商j产品i的库存量,那么联合补货时零售商j产品i的每次采购应该承担的采购成本为

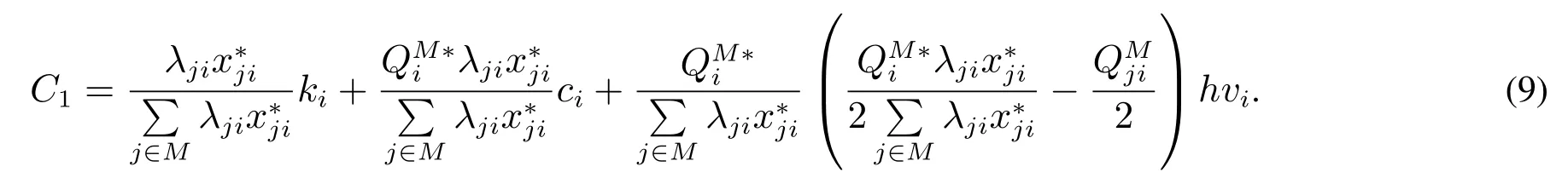
式(9)右边的第2 项是零售商j每个周期产品i的需求量,而是存储在零售商j的产品i库存量.若是零售商j库存空间里的存储量比需求量大,那么说明零售商j的部分库存空间被其他零售商所用,被占用的库存产生的库存成本需要其他零售商对零售商j进行补偿,式(9)右边的第3 项即是零售商j获得补偿库存成本的费用.若是需求量比库存量大,那么零售商j获得的该项费用表示零售商j对其他零售商的库存成本的补偿,这样就能保证零售商j承担了自己产品产生的存储成本,从而达到零售商单位时间产生利润φj的目标.

ξj是联盟库存容量不足的情况下零售商j最终分配到的利润,合作联盟同样通过零售商支付采购成本来达到利润的分配.因此,下面计算零售商j每次采购产品应该支付的采购成本.

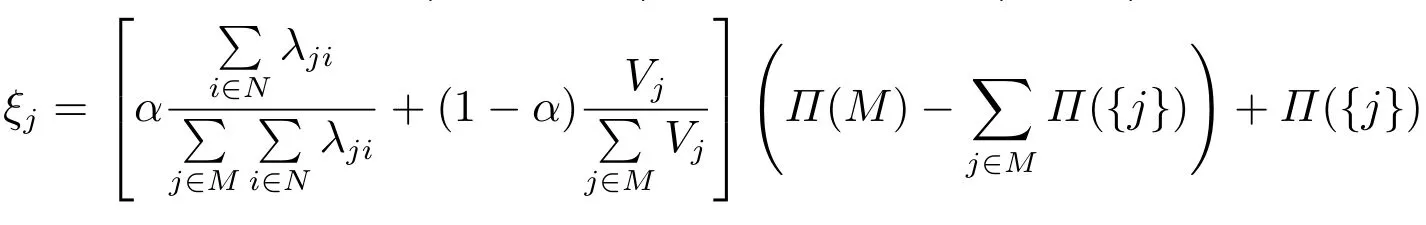
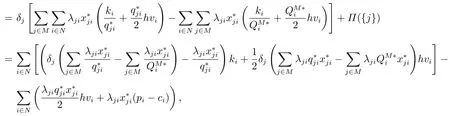
那么零售商j产品i单位时间内需要承担的成本为

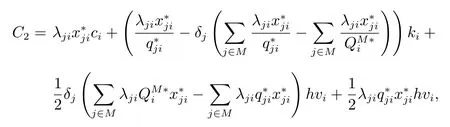
而一个周期需要承担的成本为

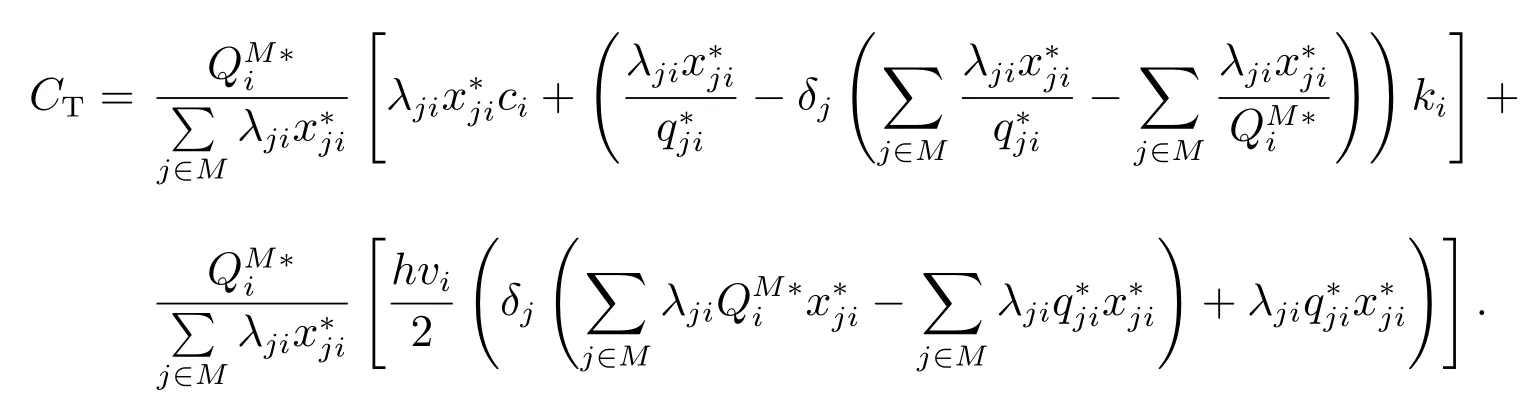
CT是采购成本和存储成本之和.而这个周期内零售商j自己库存会产生存储成本所以联盟每次采购产品i时零售商j应该承担的采购成本为

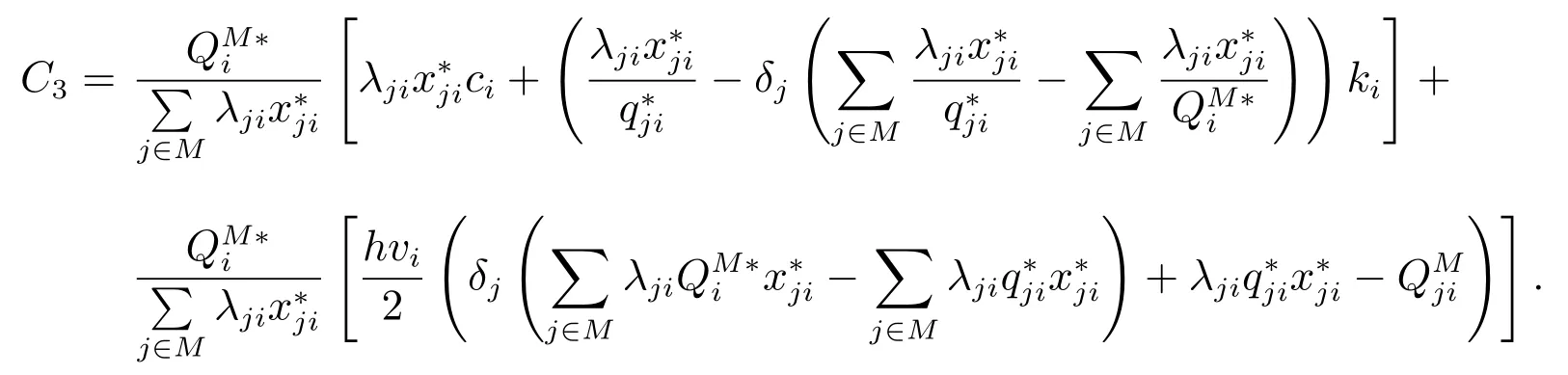
通过定理2 的证明可知, 这个收益能保证合作后的利润全部分配完, 每个零售商的利润都能够增大, 并且当联盟的库存容量充足时任何子联盟收益都不会比参与大联盟合作的收益更大.因此, 对于理性的零售商来说, 这样的核分配方案能够促使他们形成稳定的合作.尽管定理2 中的核分配方案是需要联盟库存容量充足的条件, 但这个给定条件并不会太苛刻.当参与联合补货的零售商越多,条件越容易达到,这是因为根据算法1 的计算过程,在单独决策时零售商最多只有一种产品的订货量不是而联合采购通常能够减小零售商的订货量,从而节省库存容量使得最后一种产品也经常能达到最优订货量.下面用一个简单例子来说明合作之后减少了库存水平.

例1若三个零售商决策购进五种产品, 这五种产品的最小订货量分别取qmin= 60,50,60,30,20, 产品售价p= 10,25,25,25,25, 单位产品的采购费用c= 2.500 0,6.250 0,6.250 0,6.250 0,6.250 0, 产品体积v= 0.100 0,0.250 0,0.050 0,0.500 0,0.350 0, 固定采购费k= 100,50,10,50,90, 各零售商库存容量V=30,60,45,单位体积单位时间的库存成本h=1,各零售商的需求到达率为

当零售商单独决策时,通过算法1 可得到他们的采购量为

当三个零售商库存容量都增加到75 时,他们单独决策式的采购量为

这说明当库存容量充足时所有产品都是能够盈利的, 而库存容量为30,60,45 时, 零售商的库存容量是不够的, 因为他们都选择放弃采购至少一种产品.而当他们联合采购时, 各产品的总采购量为Q= 94.701 5,64.477 9,60.000 0,76.124 6,130.193 7, 占用库存容量为112.219 7, 比他们的总库存容量135 小.联合采购是在零售商确定了采购产品之后发生的,当零售商们选择的产品都高度一致时,联盟库存容量总是会有剩余的,说明总库存水平降低了.但当零售商选择了很多不一样的产品导致能形成联合采购的产品比较少,这样联盟库存容量不够的概率会增加,如下面的例2.

例2若两个零售商决策购进三种产品, 这三种产品的最小订货量都为0, 即qmin= 0,0,0, 产品售价p=60,120,140,单位产品的采购费用c=10,15,20,产品体积v=1,1,1,固定采购费k=50,50,50,各零售商库存容量V=80,80,单位体积单位时间的库存成本h=1,各零售商的需求到达率为当零售商单独决策时,通过算法1 可得到他们的采购量为当零售商联合采购量时,三种产品的联合采购量分别为3,57,100,联盟的库存容量是不足的,只有产品3 形成了联合采购.若需求到达率为16,13,0 的零售商3 加入联合采购联盟,并且零售商3 的库存容量为70.单独采购时,零售商的采购量为34,36,0,没有达到其最优采购量40,36,0.但当三个零售商一起联合采购时,合作联盟的采购量为60,70,100,正好达到无库存容量限制下各产品的最优采购量,这个联盟的库存容量是充足的.这时候产品1,产品2 和产品3 都形成了联合采购,节省了更多的库存容量空间.

定理2 给出的分配方案在联盟库存容量不足的情况下只是满足个人理性的有效分配方案,无法保证联盟的稳定.并且是很难找到核分配方案的,这是因为通过第2 节对模型(Pj)的分析容易知道在库存容量不足时,目前也无法确定能找到多项式时间内的算法能够求解CP(M)的最优解.而近似解是有可能导致子联盟R(R ⊆M)比大联盟M得到更优的解从而发生子联盟R的总利润比大联盟M的利润更大,这种情况下找核分配方案是不现实的.

定理2 中给出的分配方案φ= (φ1,φ2,...,φm)实际上也是联合采购联盟库存容量不足情况下满足个人理性的有效分配方案.但使用分配方案ξ= (ξ1,ξ2,...,ξm)是因为这个分配方案能够激励参与联合采购的零售商共享库存容量(α<1).ξj的表达式中很容易看到零售商j的库存容量占联盟的库存容量比例越大收益就会越多.在库存容量不足的情况下,库存容量是联合采购的稀缺资源,增大库存容量会增加联合采购联盟的利润.因此有必要通过利润来激励零售商共享其真实的库存容量.而在库存容量充足时,库存容量不再是稀缺资源,无法通过增加库存容量来提高联盟的利润,若是通过利润激励零售商会导致零售商虚报库存容量而造成分配的不公平.

5 数值实验

5.1 零售商单独决策的算例分析

本节通过数值算例调查库存容量和最小订货量对零售商利润的影响.下面给出一个10 种产品的例子,其中h=1,V=75,其它参数如表1.本节没有特别说明都使用表1 中的参数值以及h=1,V=75.

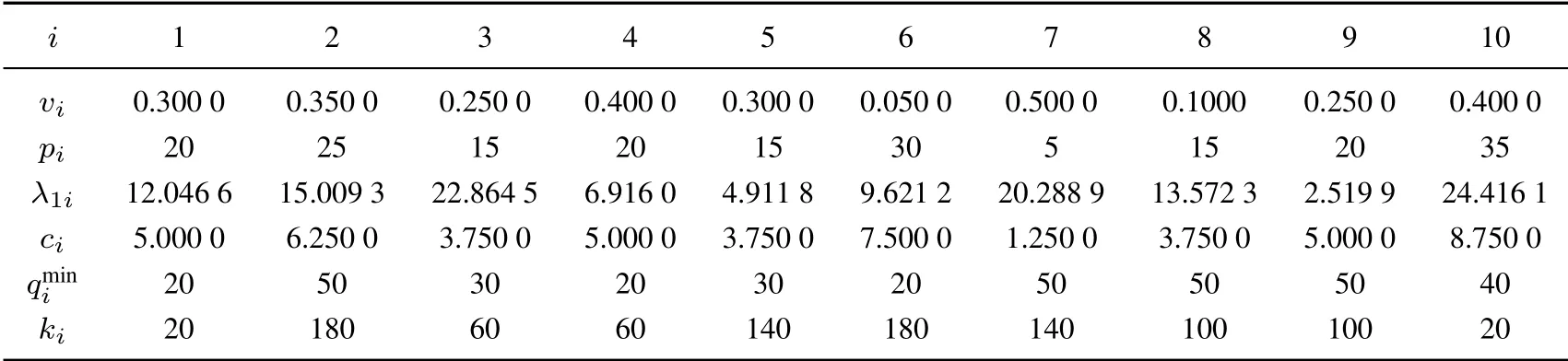
表1 模型(Pj)的参数值Table 1 Parameter values of the model(Pj)

首先研究供应商的最小订货量对零售商的影响.将产品1 的最小订货量从4 增大到200,得到零售商1的总利润曲线图,如图1.可以观察到零售商的总利润变化在区间[20,72]内.为进一步分析这个变化过程,将零售商在供应商最小订货量区间[20,72]内的最优订货量计算出来,得到表2.表2 中第2 列至第11 列分别是产品1 至产品10 在产品1 最小订货量变化时的订货量.从表2 中可以看到产品1 的最小订货量为20 时,零售商产品1 的订货量为21.951 4,说明零售商最优订货量是大于供应商最小订货量的,供应商最小订货量小小于21.951 4 时不会影响零售商的决策,因此利润也不会变化.而当供应商最小订货量大于21.951 4 时,零售商的产品1 的订货量就是供应商要求的最小订货量,并且随着最小订货量增大而影响其它产品的决策,这也就造成了图1 中零售商总利润突然大幅度下降.当供应商要求的最小订货量大于64 时,产品1 被放弃采购,并且总利润反而提高了.说明之前的解并不是最优解,这是因为这种情况并没有满足定理1 的条件.

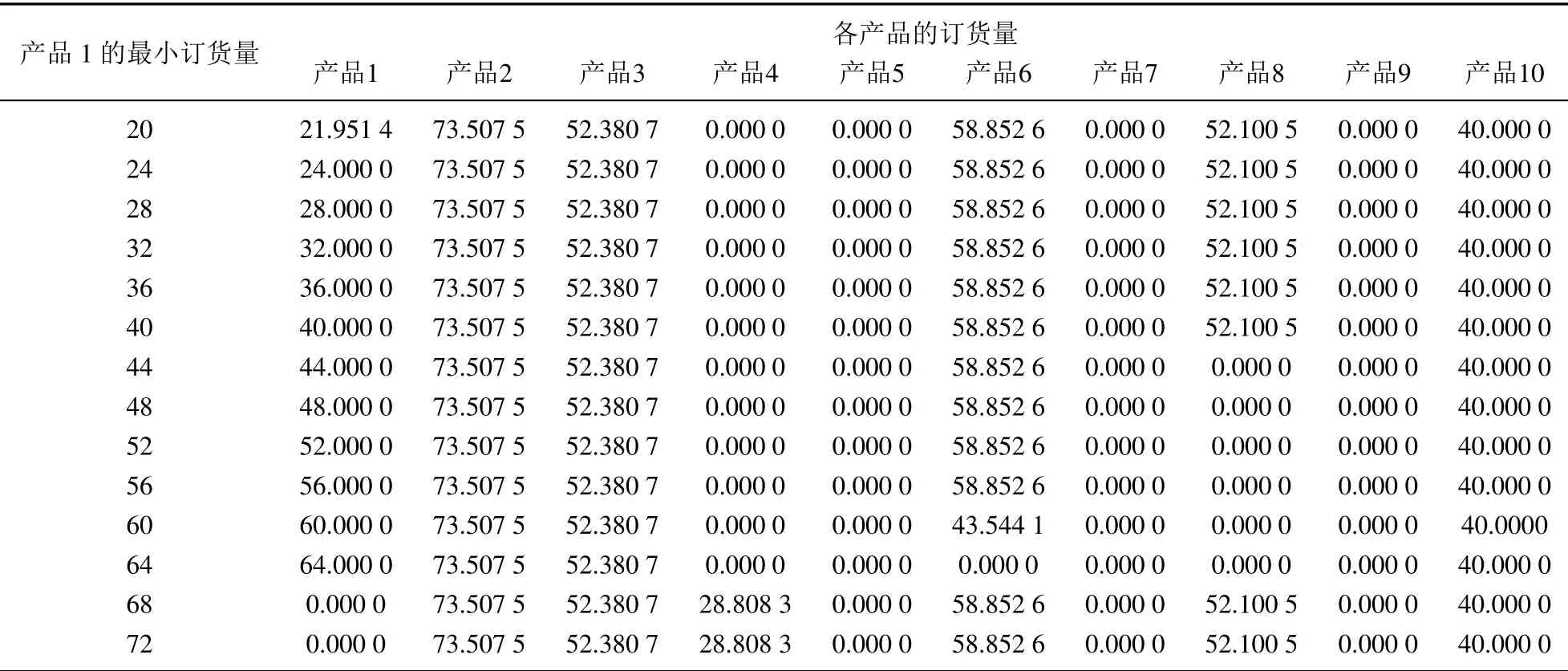
表2 产品订货量Table 2 The order quantity of product

接下来研究产品需求到达率对零售商利润的影响.将产品1 的需求到达率从0 开始增大到500,其它参数仍然用表1 的数值,另外给出了一个库存容量为150 但其它都一样的零售商的利润曲线作为对比,得到了图2.图2 中V= 75 的这条曲线整体呈上升趋势,但有的点突然下降,这是因为有的产品订货量逐渐减当减小到低于最小订货量时就会被放弃采购,而零售商总利润突然下降的点就是被放弃采购的临界点.但V= 150 时,库存容量总是充足的,产品1 的订货量上升,但没有影响的其它产品的决策.其它产品需求到达率不变的情况下,零售商的总利润随产品1 的需求到达率增大而增加.

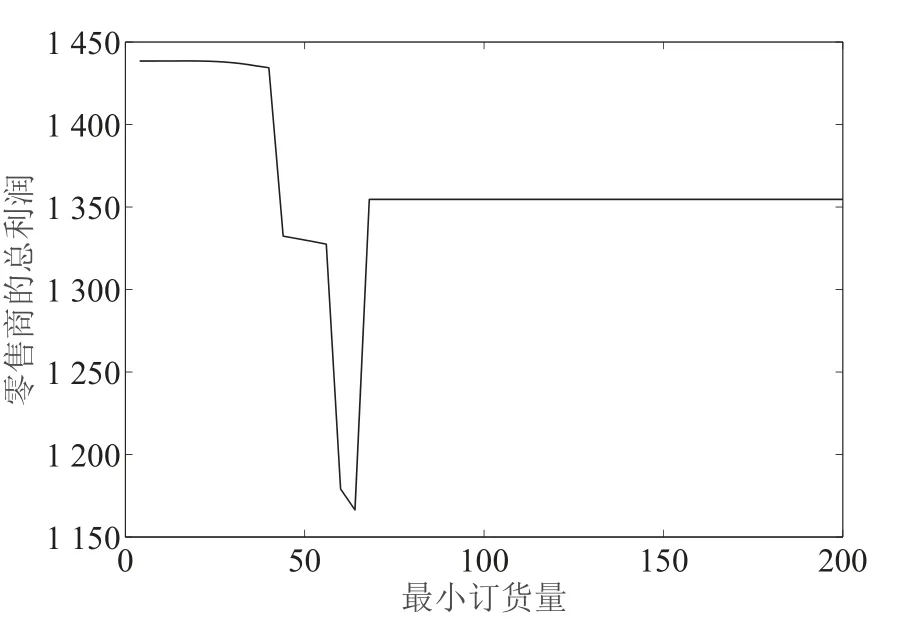
图1 产品1 最小订货量对利润的影响Fig.1 The profit affected by minimum order quantity of product 1

图2 产品1 需求对总利润的影响Fig.2 The total profit affected by demand arrive rate of product 1

通过上面的数值实验得到的结论是,在一定范围内,零售商的利润与库存容量和需求到达率正相关.

5.2 联合采购的算例分析

本节主要研究产品种类,库存容量和联盟规模对联盟合作收益的影响.本节的部分参数值取一定范围的随机数,其取值范围为λji ∈[1,25],pi ∈[5,50],ci=另外h=1,Vi=75,i ∈N.

首先研究产品种类数量和库存容量对联盟利润的影响.|M|=10,产品种类数量|N|分别取5,10,20,50,100,500,为方便计算,所有零售商的库存容量取一样的值,其值分别取75,150,300,600.产品种类和库存容量各取一个值,h=1,其它参数随机产生,计算合作后利润增长比率,每一组做100 次,取平均值,得到表3.将表3 中的数据纵向对比,可以看到,当产品种类为5 和10 时,库存容量增大并没有帮助联盟获得更大收益,而产品种类大于20 时,联盟收益随库存容量增大而增大.这是因为产品种类为5 和10 时,库存容量总是充足的,所以增加库存容量并不能帮助联盟提高收益.而产品种类大于20 时,库存容量不足导致每次采购量受限,增加了采购频率,从而增加了成本.当库存容量增大时能够帮助联盟减小成本二获得更高收益.然后进行横向对比,观察表3 中每一行的数据,可以看到,每一行从左到右,联盟的利润增长率整体都是呈下降趋势的.这是因为当产品种类很多时,零售商的选择更广了,尤其当库存容量不足时,产品种类越多,选择相同的产品概率就越低.在极端情况下甚至可能所有的零售商都采购不同的产品,从而无法形成联合采购.

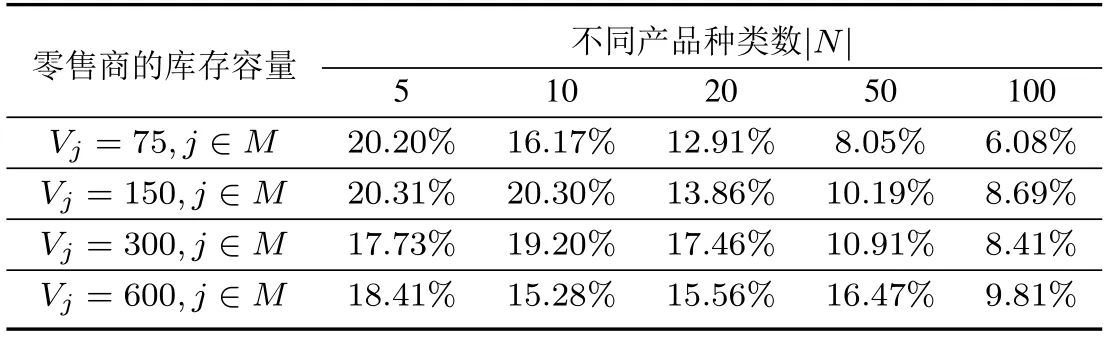
表3 产品种类数量和库存容量对联盟收益的影响Table 3 The profit affected by product category quantity and inventory capacity

接下来研究联盟规模对联盟收益的影响.联盟成员数|M|分别取5, 10, 20, 50, 100, 500,h= 1,Vj=150,j ∈M,|N|= 10,100,其它数据随机产生,同样每组做100 次,联盟利润增长率取平均值,得到表4 的数据.可以观察到表4 中联盟利润增长率是随联盟规模增大而增大的.通过表4 可以看到仅有产品种类为100,联盟成员数为5 时,才存在联盟库存容量使用完以及零售商出现负增长的情况,而其它情况下库存容量总是有剩余的.而定理2 证明了库存容量充足,并且最优订购量大于供应商的最小订货量的情况下,本文的分配方案总是在联合采购博弈的核中的.这也意味着当联盟规模较大并且联盟成员采购的产品高度集中(有较多的零售商采购同一种产品)时,总是能够保证设计的分配方案是核分配方案,因为联盟规模较大时更容易达到供应商最小订货量要求.并且当采购产品种类比较小时,会有更多的零售商采购同一种产品,能够节省更多的库存容量.

表4 联盟规模对收益的影响Table 4 The profit affected by coalition scale

通过上面的实验,可以看到,产品种类越少,库存容量越大,联盟成员越多,联合采购提高的利润越多;联合采购最高可以提高联盟总利润的26%.并且可以看到零售商数量大于10 时,再也没出现库存容量不够的情况了,这说明参与合作的零售商较多时,联盟出现库存容量不够的概率较小.

这些数值实验都是使用MATLAB 2015b 实现的.通过MATLAB 计时函数tic 和toc, 算法1 求解10 000 种产品的单独采购决策模型只需要27 s, 而算法2 求解10 000 种产品, 100 个零售商的联合采购模型也只需大概660 s 完成.这说明算法1 和算法2 的效率是非常高的,能够满足比较大规模的计算要求.

6 结束语

本文研究了库存容量和最小订货量约束的产品选择和联合采购问题.首先建立了一个多产品选择的模型,通过该模型零售商单独决策需要购进哪些产品以及其购进量.然后设计了一个多项式时间算法求解该模型,并证明了在文中给定的三种情况下该算法得到的解是最优解.为了帮助中小型企业提高利润,建立了库存共享下的联合采购决策模型并证明了该模型能够提高合作联盟的总利润.为激励零售商形成合作联盟,分别为联盟库存容量充足的情况下设计了核分配方案和联盟库存容量不足的情况下设计了满足个人理性的有效分配方案.数值实验表明联合采购总是能够提高联盟的利润并且当参与合作的零售商越多,合作联盟提高的利润越高.

本文的一些假设一定程度上限制了模型的应用.首先假设零售商采用统一零售价进行销售,这限制了联合采购产品的种类,对于许多产品零售商会选择自主定价.其次在资源限制中并没有考虑资金限制,并且在联合采购模型中,并没有考虑库存共享时产生的转运成本.这几个因素会使模型更加的复杂和难解,但也会更贴近现实,是值得继续深入研究的.