基于贝叶斯估计的威布尔更新过程统计控制
曹程明, 马义中
(南京理工大学经济管理学院,江苏南京210094)
1 引 言
在高质量过程监控中,监控事件间隔时间是一个重要问题[1].当事件发生率不为定值时,用威布尔分布描述事件间隔时间更为合适.Woodall 等[2]、Ali 等[3]建议研究威布尔分布的TBE 控制图.威布尔更新过程由一系列独立同分布的威布尔分布的事件间隔时间构成,其在产品、设备或者生产系统的可靠性建模及监控中广泛应用[4].
威布尔分布的形状参数与产品的失效机制紧密相关,形状参数的变化往往意味着所监控的产品或系统的根本性的变化,因此相比较于监控样本均值,监控威布尔分布的形状参数更有意义[4].Pascual[5]将威布尔分布转换成最小极值分布,然后基于样本极差得到1/β的无偏估计量作为监控统计量,设计了EWMA 控制图监控威布尔分布的形状参数.Pascual 等[6]和Pascual 等[7]采用了相似的方法,将样本极差作为监控统计量对威布尔分布的形状参数进行监控.但是应用这些控制图时,为了得到控制限需要进行复杂的计算.为了避免复杂的计算,Zhang 等[4]利用形状参数的枢轴量构建了一个近似服从正态分布的统计量,并在此基础上设计了Beta 控制图,仿真分析结果说明Beta 控制图能够有效的探测到威布尔分布形状参数的偏移.但是其研究中只应用20 个过程稳定时的样本数据估计过程参数,且没有分析参数估计对其所设计的控制图性能的影响.由于参数估计量固有的波动,在同一设计方法下设计出的控制图的性能将呈现差异,这称之为使用者与使用者之间的波动.这种波动使得使用者不能确定所设计控制图的错误警报概率,影响其对控制图的信心.
在应用控制图的第一阶段,收集大量的样本数据通常是不现实的,贝叶斯估计利用了过程的先验信息,可以减少参数估计对控制图性能的影响[8].Raubenheimer 等[9]设计了Bayesian c 图,分析结果表明Bayesian c 图具有良好的性能.Kumar 等[10]设计了Bayesian-Tr 控制图,分析结果表明Bayesian-Tr 控制图的性能优于传统的Tr 控制图.Lee 等[11]设计了基于贝叶斯理论的Bernoulli CUSUM 控制图,提高了控制图的性能.
针对威布尔更新过程,考虑威布尔分布形状参数偏移的探测问题以及实际中样本数据较少的问题,本文在Beta 控制图的基础上,结合贝叶斯理论,设计了Bayesian-Beta 控制图监控威布尔更新过程的形状参数.首先,给出了Bayesian-Beta 控制图的统计设计方法及其监控程序;其次,给出了过程参数的贝叶斯估计方法;然后,应用AARL 和SDARL 及蒙特卡洛仿真分析了参数估计对控制图性能的影响,结果表明Bayesian-Beta控制图受参数估计量波动的影响更小,所提出的贝叶斯估计方法中先验信息的误差对控制图性能的影响小,可操作性强;最后,用实际案例说明Bayesian-Beta 控制图在实际中的应用.
2 Bayesian-Beta 控制图的设计
2.1 监控统计量
两参数威布尔分布的密度函数如下
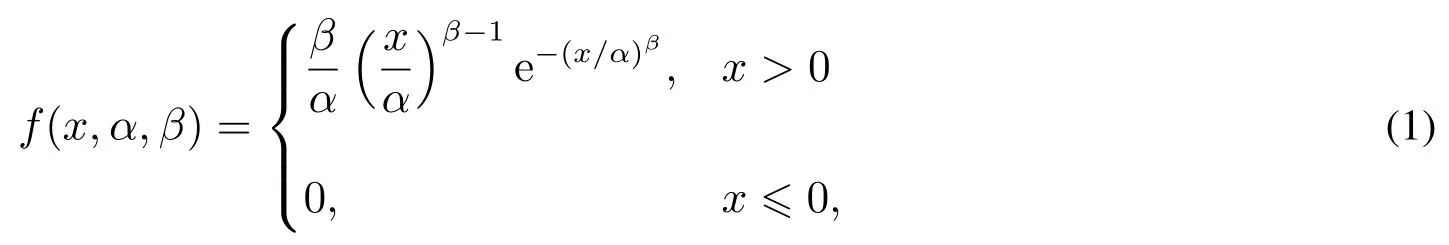
其中α,β >0,分别是威布尔分布的尺度和形状参数.
令{x1,x2,...,xn}为威布尔分布的一组样本值,则α和β的极大似然估计α和β可由下式得到,即
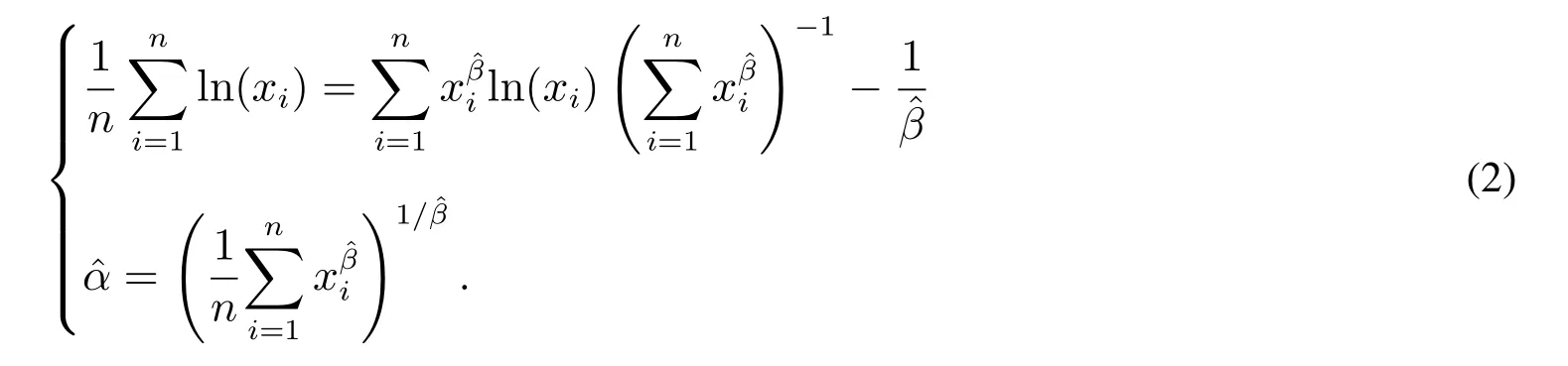

Zhang 等[4]的仿真实验表明,λ=−0.5 时,近似服从正态分布.的均值Ec[]和方差Varc()分别为其中En=E[(/β)λ],Vn=Var[(/β)λ].(/β)λ是枢轴量,因此En和Vn可通过蒙特卡洛仿真得到.En和Vn的参考值可参照文献[4].
2.2 控制限的设计
对于一系列来自威布尔更新过程的事件间隔时间的数据,设定窗口大小为n,{x1,x2,...,xn}为第一个样本,{x2,x3,...,xn+1}为第二个样本,依此类推,根据式(3)可计算统计量S的值.由2.1 节可知统计量服从均值为的正态分布.Zhang 等[4]设计了Beta 控制图,其上控制限UCL和中心线CL 以及下控制限LCL 分别为
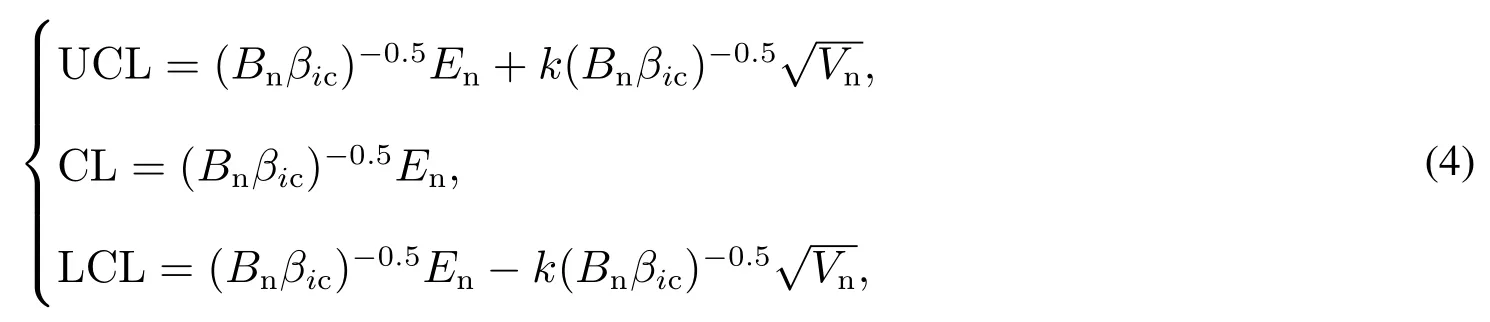
其中n为计算监控统计量的窗口大小,其中k为控制图系数.
显然控制图的ARL0值由n和k决定,不同n和k的ARL0值可参照Zhang 等[4].βic为过程受控时的β值.在应用控制图的第一阶段,收集大量的样本数据通常是不现实的,为了利用过程的先验信息,本文使用贝叶斯方法估计β值,设计Bayesian-Beta 控制图,其控制限的设计与Beta 控制图相同.
2.3 控制图的监控程序
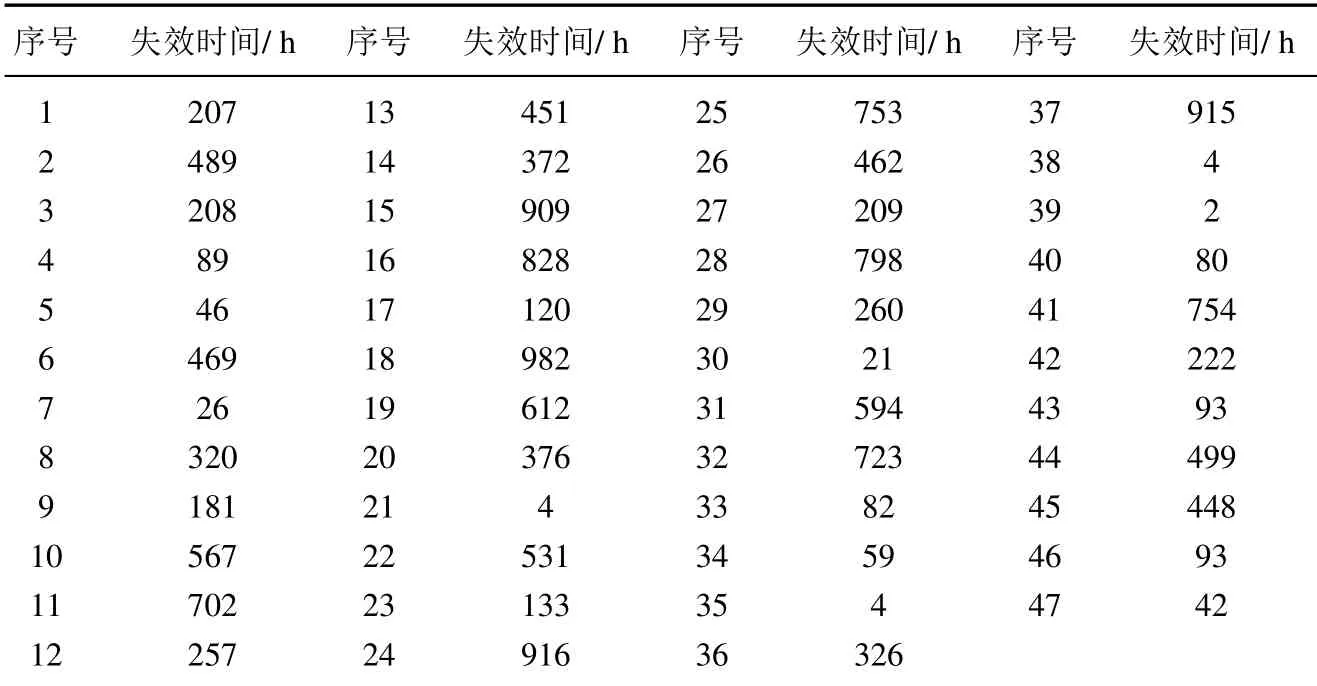
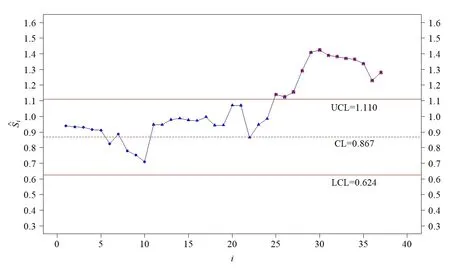
质量控制的第一阶段: 确定过程的受控状态.首先根据第一阶段的m个样本数据得到参数β的贝叶斯估计值;然后选取合适的窗口大小n和系数k计算控制限、打点,判断过程是否受控,若有异常点且异常点是由异常原因造成,则需要查找异常原因并消除,调整生产参数,采集数据重新估计参数β,计算控制限和打点,直到确定过程处于受控状态,将此时的作为过程参数的估计值,开始第二阶段的监控.第二阶段:监控阶段.计算,打点,若打点值超出控制限,则可判断过程失控,查找失控原因,采取措施使过程回到受控状态(当i 式(4)是建立在已知参数βic的基础上,在实际中参数βic通常是未知的.假设X=(x1,x2,...,xm)为第一阶段的样本数据. 令θ=1/αβ,则式(1)变为 假设参数θ的先验分布为伽马分布Gamma(c,d),c,d>0,β的先验分布为伽马分布Gamma(e,f),e,f >0 且独立于θ[13].可得θ和β的联合后验密度为 因此,θ和β的后验密度为 在平方损失下,β的点估计为其后验分布的均值.这里采用独立链M-H 算法从其后验密度中对β进行采样,具体步骤如下: 步骤1任意选择一个初始值β(i),并令i=0; 步骤2从伽马分布Gamma(e,f)中生成一个备选值β∗,并从均匀分布U(0,1)中抽取u; 步骤3若u≤a(β(i),β∗),令β(i+1)=β∗,否则令β(i+1)=βi,接受概率为 步骤4令i ←i+1,并返回到步骤2,重复步骤2、步骤3,M=10 000 次. 则参数β的估计值为 令prior(β)和prior(α)分别为β和α的先验值,MLE(β)和MLE(α)分别为参数β和α在样本X=(x1,x2,...,xm)下的极大似然估计.则β和θ先验分布的参数值可由式(5)和式(6)得到 过程受控时,为了分析参数估计对控制图性能的影响,考虑当第一阶段的样本数m为20,50,100,200,250 和500, 参数β真实值分别为0.5, 1 和2 时控制图的性能.不失一般性, 令α= 1.表1、表2 和表3分别是n= 11,k= 2.2;n= 15,k= 2.1 和n= 20,k= 2.0 即ARL0= 100 时Bayesian-Beta 控制图的AARL 和SDARL 值.为了比较Bayesian-Beta 控制图(贝叶斯估计)和Beta 控制图(极大似然估计)的性能差异,表1、表2 和表3 同时给出了Beta 控制图的AARL 和SDARL 值.具体的仿真步骤如下: 步骤1初始化m,n,k,β,α,并令先验值为prior(β)=β和prior(α)=α; 步骤2生成m个第一阶段的样本数据,估计过程参数后进入过程监控阶段; 步骤3产生一系列监控阶段的数据,计算并打点,当点超出控制限时,认为过程失控,此时的i为运行链长,; 步骤4重复步骤3 共10 000 次,计算i的均值得到ARL; 步骤5重复步骤2 到步骤4 共2 000次,计算ARL 的均值和标准差得AARL 和SDARL. 从表1、表2和表3 中可以看出随着样本数m的增大,Bayesian-Beta 控制图和Beta 控制图的AARL 逐渐接近100,SDARL 越来越小,即随着样本数m的增大,参数未知的Bayesian-Beta 控制图和Beta 控制图的性能越来越接近参数已知的情况.对比Bayesian-Beta 控制图和Beta 控制图的性能可以发现Bayesian-Beta控制图的AARL 更大,SDARL 更小,例如,当m=20,β=0.5 时,Bayesian-Beta 控制图的AARL=75.73,SDARL = 26.53, Beta 控制图的AARL = 63.63, SDARL = 30.79, 说明用贝叶斯估计可以有效降低参数估计对控制图性能的影响.Zhang 等[14]建议SDARL 值应小于设定值ARL0的10%,对于Bayesian-Beta控制图, 当样本数m为200 时, 其SDARL 值在设定值ARL0的10%左右, 而Beta 控制图, 当样本数m为250 甚至500 时,其SDARL 值才在设定值ARL0的10%左右. 对比表1、表2 和表3 可以看出, 当ARL0相同, 窗口大小n不同时控制图的性能略有差异.当样本数和参数β相同如m= 20,β= 0.5 时,n= 11 时的AARL = 75.73, SDARL = 25.63,n= 15 时的AARL = 71.74,SDARL = 26.57,n= 20 时的AARL = 66.90,SDARL = 27.15,说明参数未知情况下,窗口大小n较小时受控状态下的控制图的性能更稳定. 表1 受控状态下控制图的性能(n=11,k =2.2)Table 1 Control chart performance in controlled state(n=11,k =2.2) 表2 受控状态下控制图的性能(n=15,k =2.1)Table 2 Control chart performance in controlled state(n=15,k =2.1) 表3 受控状态下控制图的性能(n=20,k =2.0)Table 3 Control chart performance in controlled state(n=20,k =2.0) 在贝叶斯估计中, 先验信息对估计结果有一定的影响.在确定参数β和θ先验分布的参数值时利用了参数β和α的先验值prior(β)和prior(α), 显然prior(β)和prior(α)会影响到控制图的性能.令δ1= prior(β)/β,δ2= prior(α)/α分别为参数β和α的先验值prior(β)和prior(α)和其真实值的误差系数.因为δ1或δ2的增大(或减小)对控制图性能的影响相同, 所以分析中考虑δ1或δ2取相同值的情况.表4 给出了误差系数δ1或δ2为(1.15,1.10,1.05,1.00,0.95,0.90,0.85)时的控制图的性能,其中n= 11,k=2.2,β=1,α=1. 表4 不同误差系数下控制图的性能对比Table 4 Performance comparison of control charts with different error coefficients 当误差系数δ1=δ2>1 时, 即参数β和α的先验值prior(β)和prior(α)大于其真实值时, 控制图的性能随着误差系数的增大越来越差, 但仍然比Beta 控制图的性能更好, 例如m= 20 时, 误差系数δ1=δ2= 1.15 的AARL = 67.51, SDARL = 25.66,δ1=δ2= 1.10 的AARL = 70.82,SDARL = 24.60,δ1=δ2= 1.05 的AARL = 73.58, SDARL = 23.32, Beta 控制图的AARL = 61.47,SDARL = 29.14.当误差系数δ1=δ2<1 时,即参数β和α的先验值prior(β)和prior(α)小于其真实值时,控制图的性能随着误差系数的减小越来越好. 综上, 采用贝叶斯方法估计参数能够有效减少参数估计量的波动对控制图性能的影响, 即使用者与使用者之间的波动问题, 增强了使用者对控制图的信心; 先验信息值的误差在真实值的15% 以内,Bayesian-Beta 控制图都有着较好的性能,说明所提贝叶斯估计方法具有可操作性. 表5 的数据是某生产系统中生产出来的硬盘驱动器的加速寿命试验的失效数据[4].取前20 个数据为第一阶段的样本数据,n= 11,k= 2.2 即ARL0= 100,计算得βic= 1.238,LCL = 0.624,CL = 0.867,UCL=1.110.剩余的数据作为第二阶段的监控数据,监控图如图1 所示. 表5 硬盘驱动器失效时间Table 5 failure times of hard disk drives 图1 中的实心圆点表示第一阶段的打点值,可以看出第一阶段过程是稳定的;其余点是第二阶段的打点值,超出控制限的打点值用方框实心点表示.图中有一个明显的上升的趋势,说明形状参数的值在减小,意味着该硬盘驱动的可靠性在提高.事实上该硬盘驱动器的可靠性确实提高了,图中的上升的趋势符合事实.可见Bayesian-Beta 控制图对过程偏移具有较好的探测能力. 图1 某硬盘驱动器的生产过程监控图Fig.1 The control chart of a hard disk drives’production process 针对威布尔更新过程,考虑威布尔分布形状参数偏移的探测问题以及实际中样本数据较少的问题,设计了Bayesian-Beta 控制图,给出了控制图的监控程序和参数的贝叶斯估计方法.相比较于Beta 控制图,在过程受控时Bayesian-Beta 控制图的AARL 更接近于ARL0,SDARL 更小,即Bayesian-Beta 控制图的性能受参数估计量波动的影响更小.所提出的贝叶斯估计方法中先验信息的误差对控制图性能的影响小,可操作性强.案例分析表明Bayesian-Beta 控制图在实际应用中能够有效探测到过程的偏移. 由于监控统计量之间的相关性,本文未能给出ARL 的理论计算方法,另外如何处理数据之间的相关性是一个需要进一步研究的问题.3 贝叶斯估计
3.1 参数估计的步骤
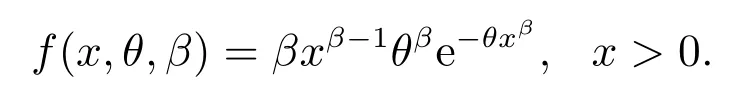
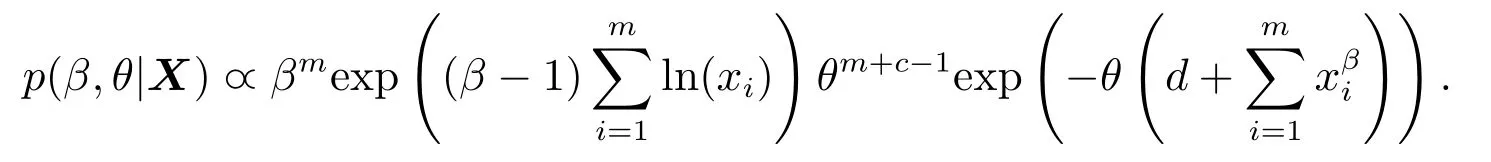
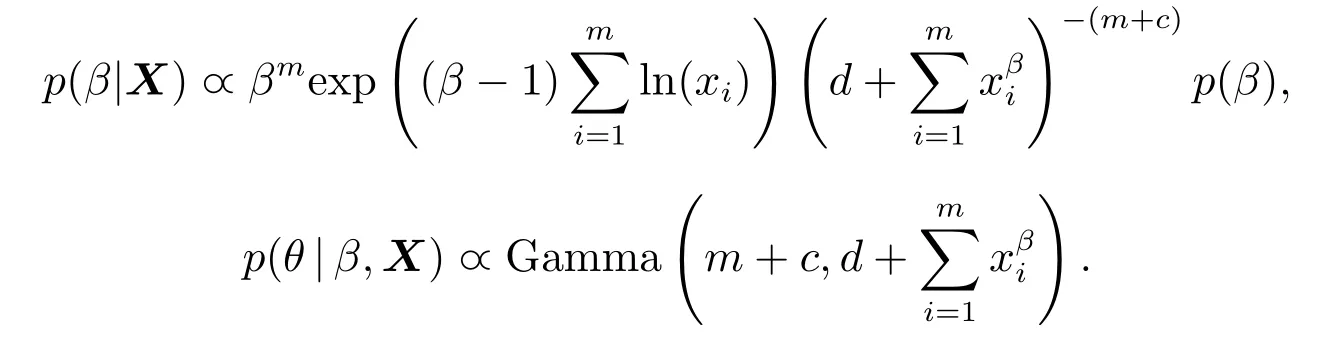
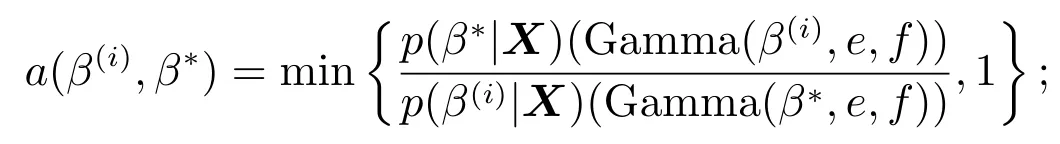
3.2 先验分布参数的取值
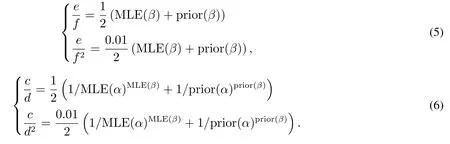
4 控制图的性能分析
4.1 受控状态下控制图的性能分析
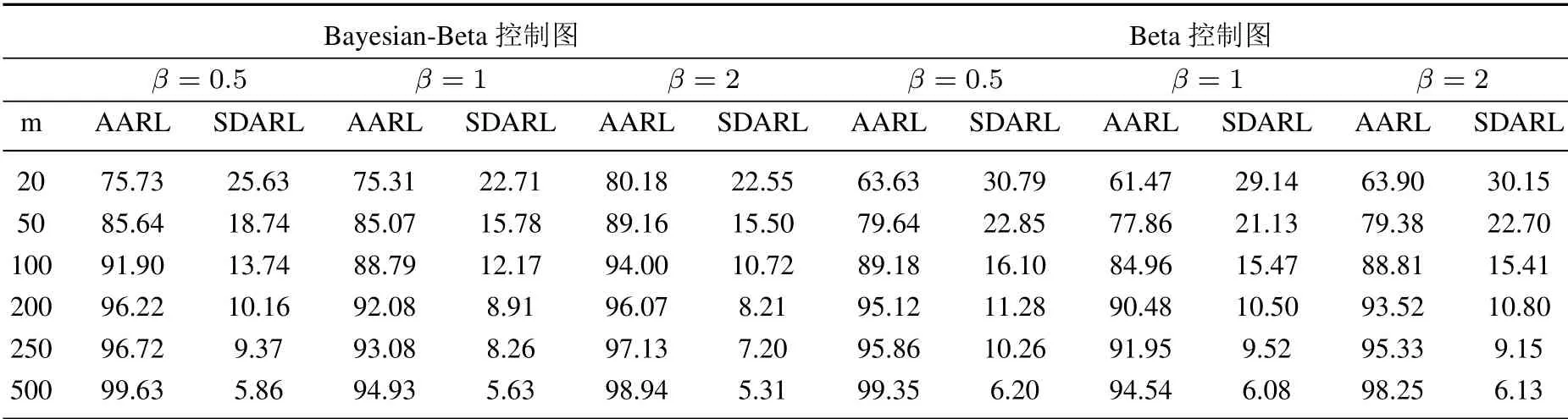
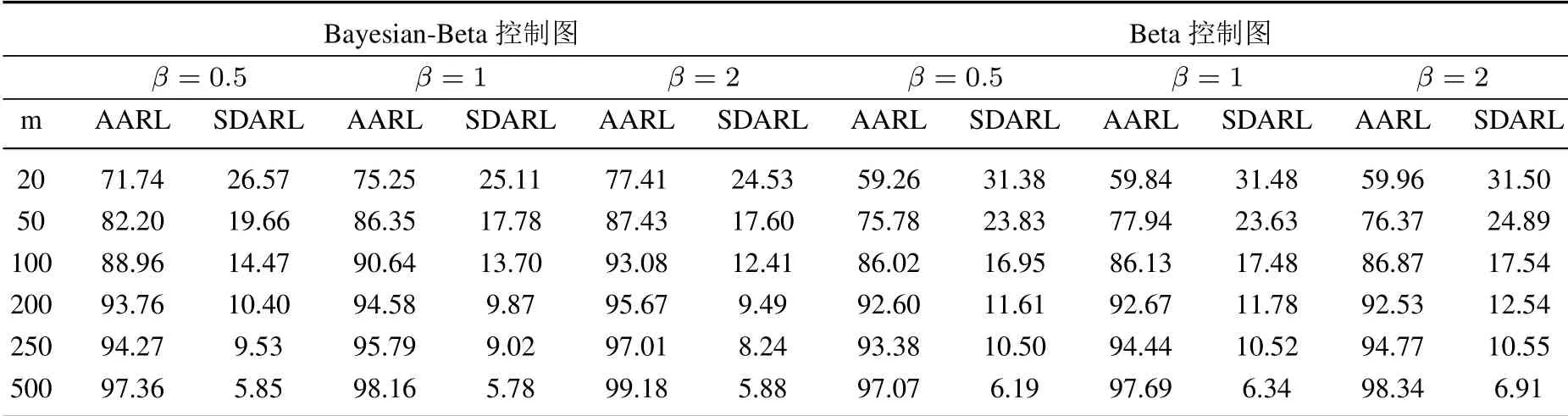
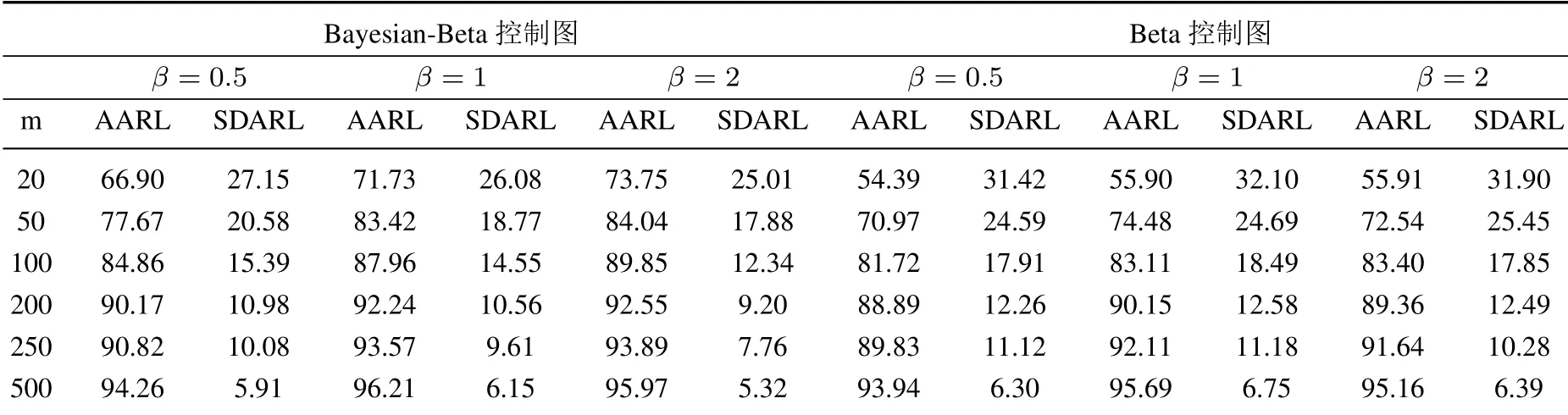
4.2 先验信息误差灵敏度的分析
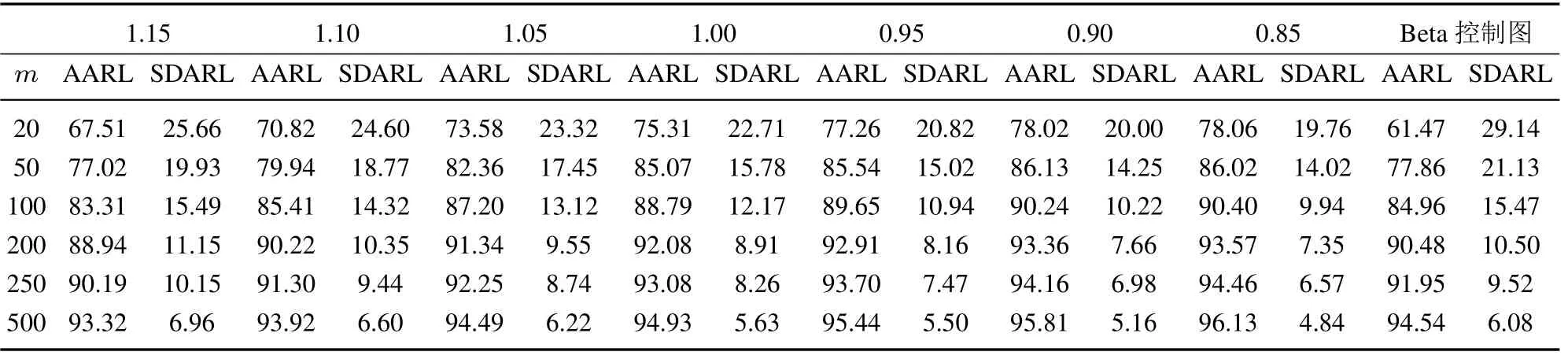
5 案例分析
6 结束语

