基于变点–算术失效强度减的设备维修质量评估

周 瑜, 寇 纲, 白 杨, 尔古打机

(1.内蒙古大学经济管理学院,内蒙古自治区呼和浩特010021;2.西南财经大学工商管理学院,四川成都611130;3.西南民族大学电气信息工程学院,四川成都610041)

1 引 言

生产设备是企业的重要资产,生产设备的运行状况严重影响企业的生产安全和效率.企业为了提高生产设备的可用度,通常对设备实施一系列的预防维修政策.据文献[1,2]统计,设备维修费用一般占全部生产成本的15%～70%,平均为20.8%.发达国家交通运输行业的数据为20%～30%,钢铁行业约为40%.同时,预防维修质量与预防维修成本之间具有一定的内在关系[3].因此,如何获得最优的预防维修质量一直是研究热点.

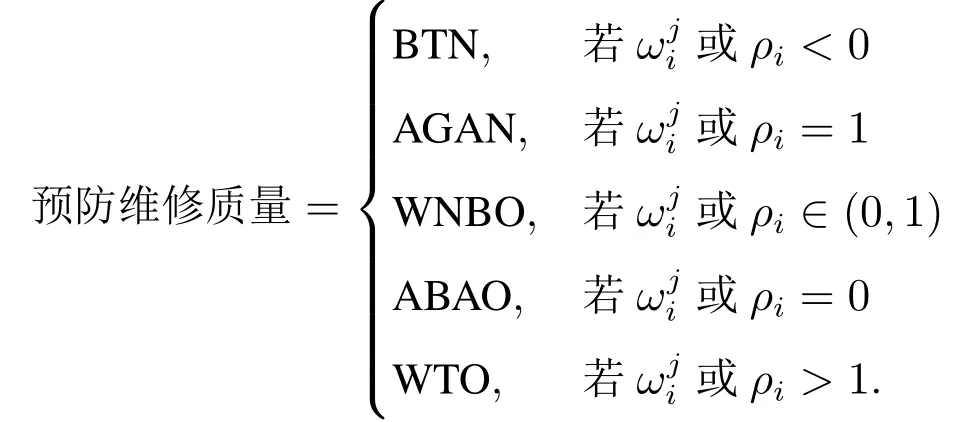
对于预防维修,设备经历一次预防维修后,设备的失效强度与预防维修之前相比通常会出现以下五种情形: 比新的好(better than new,BTN),修复如新(as good as new,AGAN),介于新旧之间(worse than new but better than old,WNBO),修复如旧(as bad as old,ABAO)和比旧的差(worse than old,WTO).其中BTN 意味着设备经历一次预防维修后,它的失效强度明显优于预防维修之前,即出现了可靠性增长现象[4,5].此状态下的常见模型为可靠性增长模型[4,5].然而,可靠性增长现象很难出现在劣化系统中.AGAN意味着设备的失效强度在预防维修后恢复到新设备的水平,即设备的状态完好如新.这种状态在电子元器件的可靠性建模中较为常见,常用的建模方法为更新过程[6,7].ABAO 表示设备的失效强度在预防维修前后无差异,即设备的状态恢复如旧.由于这种状态假设既不影响失效强度的变化趋势也不影响失效强度的变化速率,因此在设备可靠性建模中最为常见,常用的建模方法有点过程模型[8].实际上,设备经历一次预防维修后,其失效强度一般会介于新旧状态之间,即WNBO 状态,也称之为不完美维修[9].针对WNBO 状态,Wang 等[10]总结了已有建模方法,读者可以通过该文献进一步了解这些方法.WTO 状态是五种维修状态中最不理想的一种状态.WTO 状态意味着设备在执行预防维修后,设备的失效强度较预防维修之前相比出现明显的劣化趋势.

以上五种情形中,关于不完美维修的应用和研究最常见,现有文献开发了许多经典模型,如Kijima 模型[11,12],BP 模型[13]等.Wu 等[14]把这些方法大致划分为三类,分别是年龄减模型,失效强度减模型和混合模型.基于本文模型应用的背景,本文仅就失效强度减模型进行讨论.失效强度减模型通常假设设备经历一次预防维修后,设备的失效强度将减少一确定值或与原失效强度成固定比例的减少.已有研究中,有大量的关于失效强度减的文献,如文献[15–21].Nakagawa 等[18−21]提出的失效强度减模型就是成比例减少模型,即假设预防维修后的设备失效强度减少量与预防维修前的失效强度成一定比例.Wu 等[22]建议的模型则是假设预防维修后的设备失效强度将随机减少一定量值.随后,算术失效强度减(Arithmetic Reduction of Intensity,ARI)模型被广泛应用[15−17,19,20].文献[16]在Nakagawa 等的模型基础上提出了一个p阶记忆模型,其中阶数p是指预防维修能够影响到的未来预防维修区间数.而Chan 等的模型实质上就是一种无限记忆模型.Toledo 等[17]随后给出了p阶记忆模型的极大似然估计方法和模型选择方法.Zhou 等[23]根据实际应用背景,提出了一个新的算术失效强度减模型.该模型假设设备经历一次预防维修后的失效强度等于预防维修前的失效强度和一个当量之和.这个当量与预防维修前的失效强度和设备固有失效强度之差成一定比例,进而采用该比例描述设备预防维修质量.通过与现有模型的比较说明了方法的有效性.

在上述模型和方法中, 通常假设设备的失效强度的变化是平滑的.现实中, 设备的失效强度有可能在某一时间区间上出现失效强度变化趋势不一致的情形, 这种现象被称为失效变点[24].基于此, 本文在Zhou 等[23]的工作基础上,给出了一个具有失效变点的算术强度减模型.

2 变点–算术失效强度减模型

生产设备通常具有多个不同时间周期的预防维修,简称为多级预防维修制度.以巴士车队为例,每隔15天进行一次一级预防维修;每隔3 个月～4 个月进行一次二级预防维修;每隔2年进行一次高级预防维修.为了模型构建过程的简捷,接下来将以具有二级预防维修制度的设备为例进行说明,但这并不影响该模型扩展到更多级别的预防维修制度.具有二级预防维修制度的设备发生故障和维修历程如图1 所示.在图1中,车队在171 周内共进行了7 次二级预防维修.例如,车队在第26 周,第48 周做了第1 次,第2 次预防维修.假设一次预防维修结束后,重新计算车队在该预防维修区间内的失效表现,直到下一次预防维修来临为止.因此,车队的第1 个预防维修影响下的车队失效表现区间为[0,22].由图可以看出,车队预防维修的执行并非严格按等周期进行,即预防维修周期是非齐次的.本文采用累积失效次数衡量车队失效表现,图中每一段带圈实线表示在上一次二级预防维修后和下一次二级预防维修之前,车队发生失效的累积次数.图线斜率越大,说明该二级预防维修区间内车队失效越频繁.

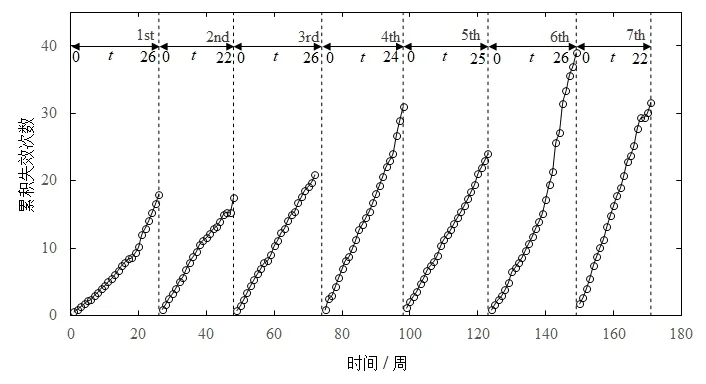
图1 设备故障和维修历程Fig.1 Equipment failure and maintenance process

根据图1,车队在第123 周进行了第五次二级预防维修.此后,车队的失效频率出现了较为明显的变化,在该二级预防维修区间内的累积失效次数高达39 次,远高于其它二级预防维修区间.实际上,引起该变化的原因是车队在该区间内发生了营运线路的变更.线路变更引起了失效频率的变化,这种变化可以看作为失效变点[24].如果不考虑变点的存在,建模得到的结果可能存在一定偏差.因此,本文将基于以下假设构建失效变点–算术失效强度减模型.

2.1 模型假设

具有二级预防维修制度的设备预防维修历程如图2 所示.

图2 设备二级预防维修历程Fig.2 Equipment type-II preventive maintenance process

根据图2, 假设设备进行第i次二级预防维修的时间为Ti,i= 1,2,...,n.假设二级预防维修为等周期预防维修, 则有T1=T2−T1=···=Tn −Tn−1.在第i个二级预防维修周期内, 设备进行第j次一级预防维修的时间为Hj,j= 1,2,...,mi.且有H1=H2−H1=···=Hmi −Hmi−1和Ti −Ti−1= (mi+1)(Hmi −Hmi−1)成立.令t为任意一个一级预防维修周期内的运行时间, 为一非负变量, 0 ≤t≤Hmi −Hmi−1.假设在t时间内每隔Δt统计一次系统的累积失效次数, 观察时间点可简记为tpj(t=pjΔt),且令Mji(t)标识观察到的累积失效次数,即令Mji(t)标记第j次和第j+1次一级预防维修区间内的累积失效次数.经历一次一级预防维修后,Mj i(t)清零并重新计算.这样,获得的失效观察次数,如表1 所示.由于实际执行过程中,预防维修区间非严格相等,因此出现观察时间点非齐次现象.例如,表1的[H2,H3]区间内,tpj中的累积失效次数为null,意味着设备在tpj来临前已经进行了预防维修.

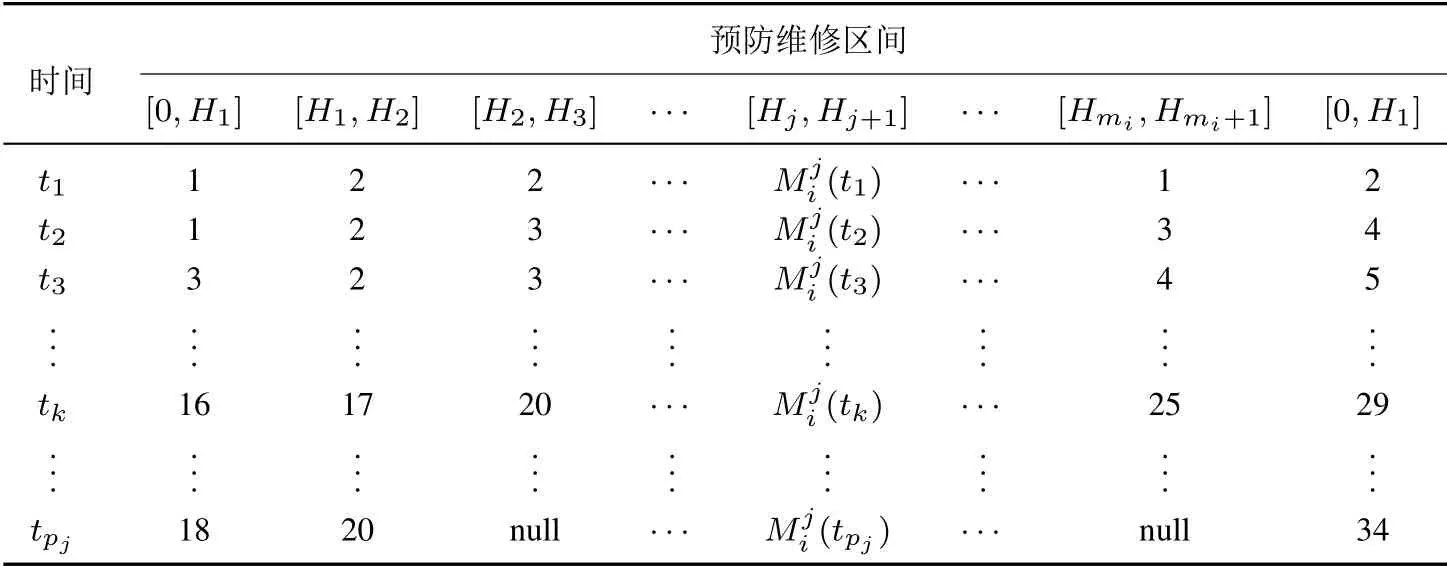
表1 累积失效次数Table 1 Cumulative failure number

此外,令(t)标识设备在第i次二级预防维修区间内进行的第j次一级预防维修区间内的实际失效强度,而设备的固有失效强度记为(t).假设设备的预防维修质量为变量,令ρi为第i次二级预防维修质量,为第i次二级预防维修区间内第j次一级预防维修质量.幂律模型的参数为αi和βi.为了方便建模,结合文献[23],还对模型做如下假设:

1)设备故障修理时间,预防维修时间和停机时间与设备的运行时间相比足够小,可以忽略不计.

2)设备故障修理因为是最小维修,因此故障修理不会本质上改变设备的固有失效强度.因此,在对设备失效强度进行建模时可以应用失效计数过程.

3)固有失效强度一般可以由进行首次预防维修前的失效历程进行确定.实际上,设备首次进行预防维修前的失效历程很难获得,即使获得也很难推断出失效的固有失效强度.因此,如果无法获得首次预防维修前的失效历程,可以将能够获得的最早失效历程作为建模固有失效强度的参考.

2.2 模型构建

根据以上假设,令设备经历一次预防维修后的失效强度等于预防维修前的失效强度和一个当量之和.文献[20]中假设该当量与预防维修前的失效强度和预测失效强度之差成一定比例,失效强度仅基于最近的预防维修区间的失效强度进行预测.由于失效强度的变化受过去所有预防维修和固有失效强度的累积影响,文献[23]在此基础上提出,该当量与预防维修前的失效强度和设备固有失效强度之差成一定比例.因此,第i次二级预防维修区间内第j次一级预防维修后的失效强度之和.

第i次二级预防维修区间内第1 次一级预防维修前的失效强度只受第i次二级预防维修影响,因此第i次二级预防维修区间内第1 次一级预防维修前的失效强度可以表达为之和.综上所述,可以得到不含有失效变点的算术失效强度减模型[23]

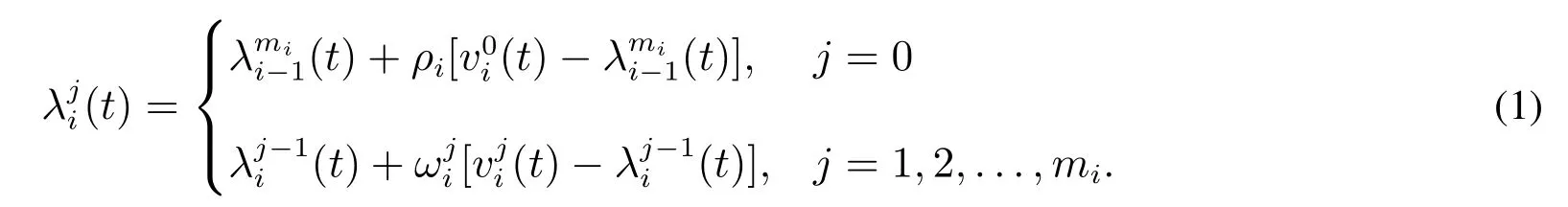
当i= 1,2,...,n时,上式成立.当i= 0 时(即无任何预防维修干扰时),根据假设3)和图2 有(t) =(t).

如果设备的运营环境,工作强度等在第i次二级预防维修区间的第j次一级预防维修后发生较大变化,从而使得设备的失效强度变化趋势发生变化,已有文献称之为失效变点[23].设备失效强度的趋势变化通常表现为短周期内两次相邻失效的时间间隔变化和长周期的趋势变化.对于短周期内的失效时间间隔变化可以引入一个尺度参数描述,而长周期的趋势变化可以引入一个形状参数进行度量.在现有失效强度模型中两参数幂律模型恰好含有一个尺度参数和一个形状参数,因此本文采用幂律模型对失效趋势进行平滑处理.平滑处理的目的是消除因设备运营环境差异或工作强度变化而带来的失效强度变化.基于式(1),可构建得到新的基于失效变点–算术失效强度减模型为

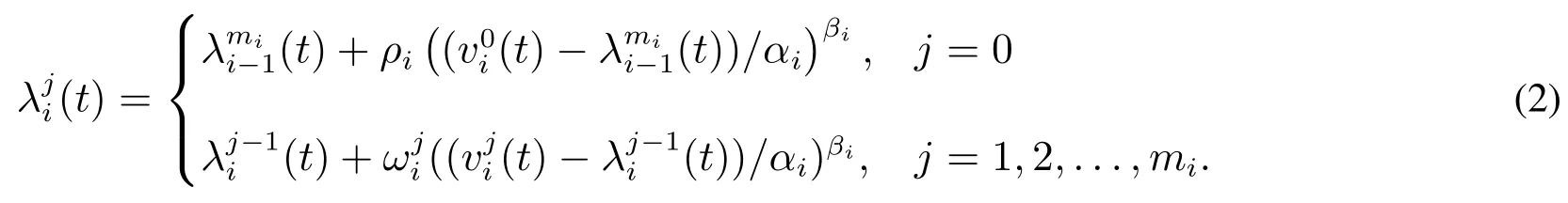
根据文献[25],失效计数过程中,失效强度为单位时间内的失效次数.故设备失效强度和失效次数存在以下关系

根据式(2)和式(3),有

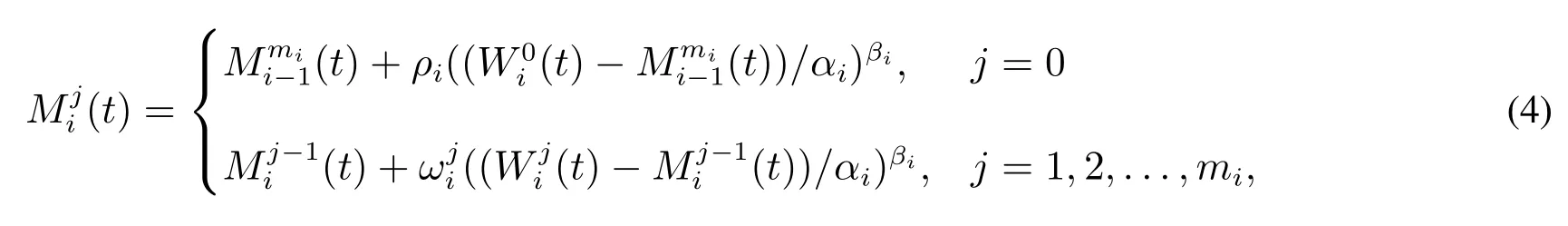
实际上,设备在运行过程中会受到预防维修的干扰,因此该值是一个理论值,可以根据初次失效强度建模得到.根据表1 和式(4),建模的具体步骤如下.

步骤1为数据转换及预处理.如果采集的失效数据为失效时间间隔数据,可以统计转换为失效计数数据,并整理得如表1 所示的数据类型.

步骤2建模数据集得到其概率分布进而应用式(4)估计观察时间点上的期望累积失效次数并确定固有失效强度.对于数据集可以采用较为常用的幂律模型或线性对数模型[3,25].同时,将能够获得的最早的预防维修区间内的失效过程确定为固有失效强度.当然,这样确定的固有失效强度与设备真实的失效强度之间必定存在一定的差异,但维修质量评估主要参考的就是维修前后的失效强度变化情况.因此,取能够获得的最早的失效过程为固有失效强度具有一定合理性.当然,固有失效强度对维修质量评估的影响值得在今后的研究中进一步探讨.

步骤3估计ρi或.根据式(4),预防维修质量可以通过最小化拟合值与观察值之间的最小误差平方和(sum of squares for error,SSE)得到.SSEij为

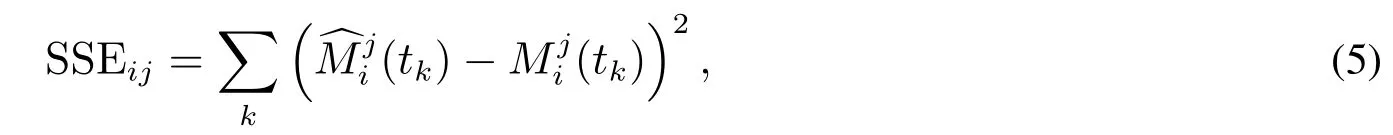
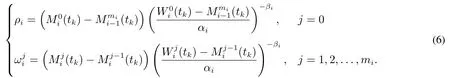
步骤4预防维修质量评估.依据估计得到的ρi或值,根据模型构建原理,可以推导当ρi或取不同值时,系统失效强度经历一次预防维修后的变化情况.举例来说,若ρi=1 或=1,系统经历第i个二级预防维修区间内的第j次一级预防维修后的失效强度就等于(t).因为(t)是系统在第i个二级预防维修区间内的第j −1 次一级预防维修干预得到的系统在第i个二级预防维修区间内的第j次一级预防维修区间内的固有失效强度表现.因此,ρi= 1 或= 1 意味着系统经历第i个二级预防维修区间内的第j次一级预防维修后,其失效强度与该区间的系统固有失效强度表现一致.因此,与上一预防维修区间相比,相当于修复如新.由此,可以推出不同ρi或值对应的预防维修质量如下:

在本文建议的模型中,对于二级预防维修ρi是通过二级预防维修后至下一个一级预防维修来临前的失效历程来衡量的.现实中,二级预防维修的实际影响区间为一个完整的二级预防维修区间.换句话说,模型中的ρi是衡量整个二级预防维修区间内的变化趋势,而是衡量整个一级预防维修区间内的变化趋势.一旦能获取充足的二级预防维修数据(至少在二级预防维修后再运行一个二级预防维修周期),可以对二级预防维修的维修效果ρi进行校对.

2.3 模型比较和验证

为了说明模型的有效性, 本文建议的模型将与相似的三个模型进行对比, 这三个模型分别来自于文献[18,20,23].文献[23]给出的模型如式(1)所示.文献[18]的模型可以描述为

其中φ是预防维修质量.文献[20]的模型是

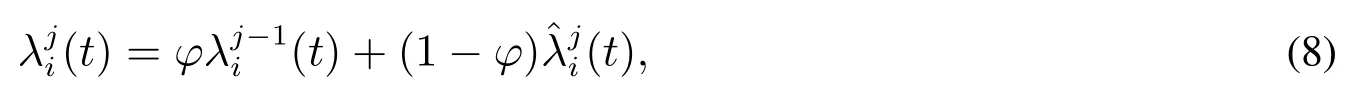
其中φ是预防维修质量.

对比几种模型,建议的模型参数的增加,势必会导致具有更优的拟合效果.为了避免此类情况的发生,可以通过构建AIC 准则或AICc 准则进行拟合优度比较.基于最小二乘法的AIC 准则[26]为

本文的建模数据样本较小,考虑基于最小二乘法的AICc 准则[26]更为恰当.基于最小二乘法的AICc 准则为

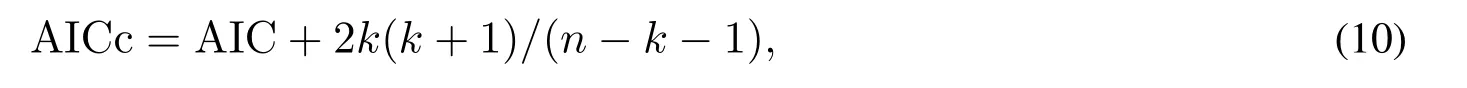
其中k为模型参数个数,n为数据样本量.一般来讲,最小的AIC 值或AICc 值,具有最优的拟合优度.

为了进一步说明建议模型与其它模型的可比性,以及对存在的失效变点进行平滑的合理性,本文分析了原始数据的平均失效时间间隔(mean time between failures,MTBF),并以两次预防维修区间内的MTBF 改进量ΔMTBF 为依据开展验证说明.这是因为MTBF是系统预防维修状况的外在表现.预防维修排除的潜在失效越多, 则系统的失效次数越少, 那么系统的MTBF 会越大.设第j个预防维修区间内的MTBF为MTBFj,则

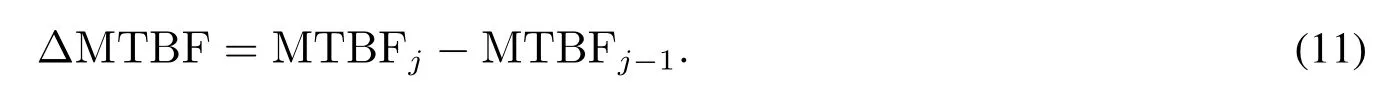
这样,如果ΔMTBF>0,则意味着系统经历一次预防维修后运行状态有改善,值越大改进程度越明显;如果ΔMTBF=0,则意味着系统经历一次预防维修后运行状态不变;如果ΔMTBF<0,则意味着系统经历一次预防维修后运行状态保持比原来更差.由于ΔMTBF 和或(ρi)具有不同的变化范围,可以将其进行0-1 标准化后进行比较.

3 数值例子

某巴士公司的管理信息系统详细记录了预防维修周期内车辆发生的故障数据和所开展的维修活动.本文收集了该巴士公司一个车队的预防维修数据.在数据收集周期内,该公司对该车队共进行了7 次二级预防维修.经过整理得到了该车队中巴士车辆在7 次二级预防维修周期内的累积失效次数,如表2 所示.表2中初始列表示车辆未进行二级预防维修前的初始失效过程,“1st”指车辆经历第1 次2 级预防维修后的失效过程,以此类推.不失一般性,对数据进行了脱敏处理,累积失效次数取的是车队所有车辆的平均累积失效次数.而这并不会影响到评估结果.此外,该车队车辆在第5 次预防维修后的运营线路发生了变化,由于两条线路的明显差异,导致车辆失效趋势发生明显变化.因此,在第5 次预防维修效果评估时,可考虑应用具有失效变点的评估模型进行处理.

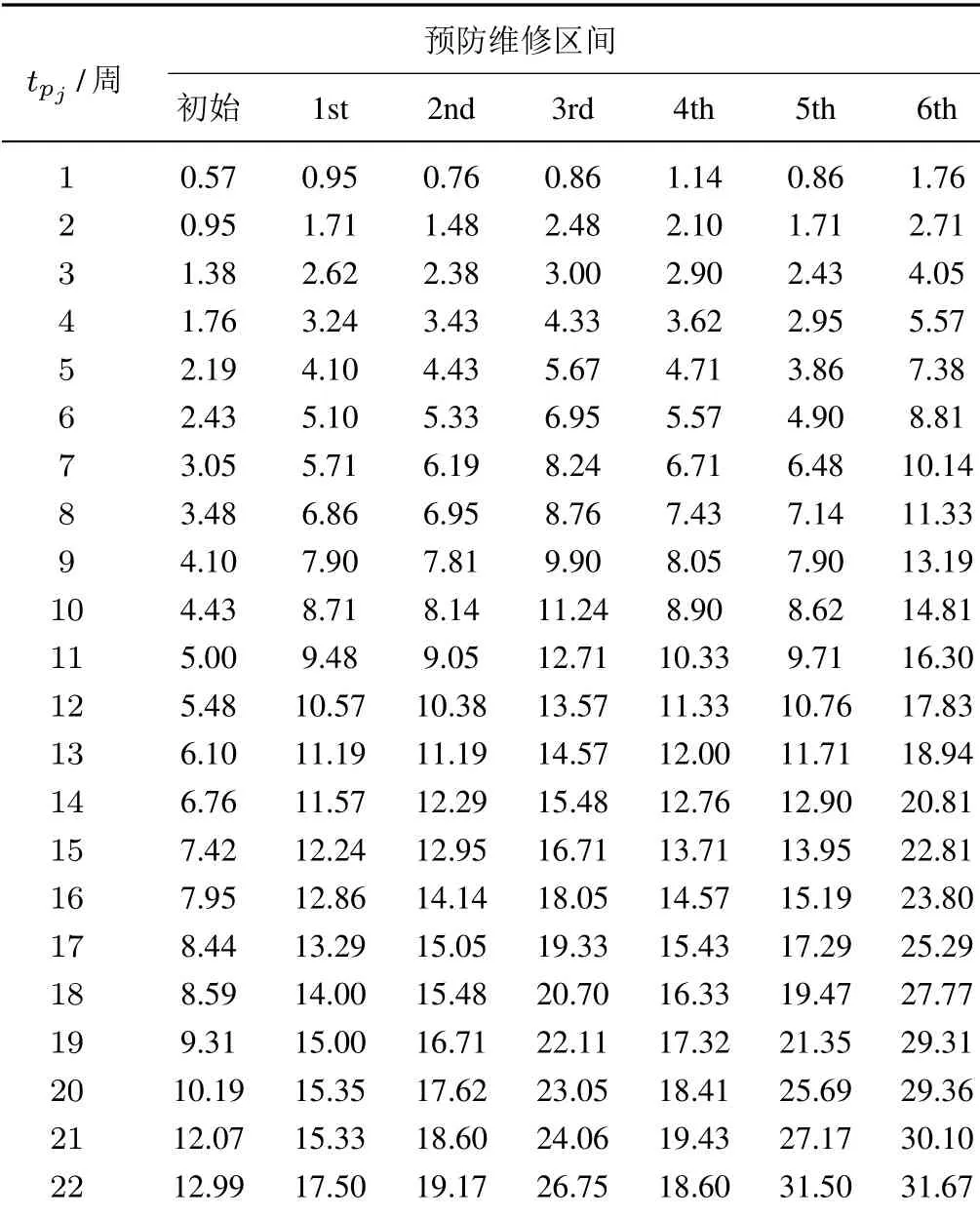
表2 巴士车辆的累积失效次数Table 2 Cumulative failure number of the urban bus

根据表2,应用幂律模型对每一预防维修周期内的失效次数进行模型,继而应用文献[18,20,23]和本文的模型估计得到了前6 次预防维修的维修质量.具体的建模步骤如下:

步骤1设将能够得到的最早的失效记录,即表2 中第一列数据确立为固有失效数据.应用三参幂律模型(tk)=((tk+θ)/φ)ψ建模(tk),参数估计得到θ=17.08,φ=17.14 和ψ=3.75.

步骤2应用文献[18,20,23]中的评估方法进行预防维修效果评估,得到的预防维修质量如表3 所示,得到的SSEi也列在了表中.

步骤3观察表3 中文献[18,20,23]估计得到的SSEi会发现,这三种方法得到的SSEi在第5 次预防维修时发生了突变.因此,可尝试使用本文建议的模型建模第5 次和第6 次预防维修质量.根据式(4),在文献[23]评估的前4 次预防维修质量基础上,进一步估计得到了第5 次和第6 次的预防维修质量,如表3 倒数第2 行和第3 行所示.在平滑建模时,参数估计得到α5=17.32 和β5=4.40.

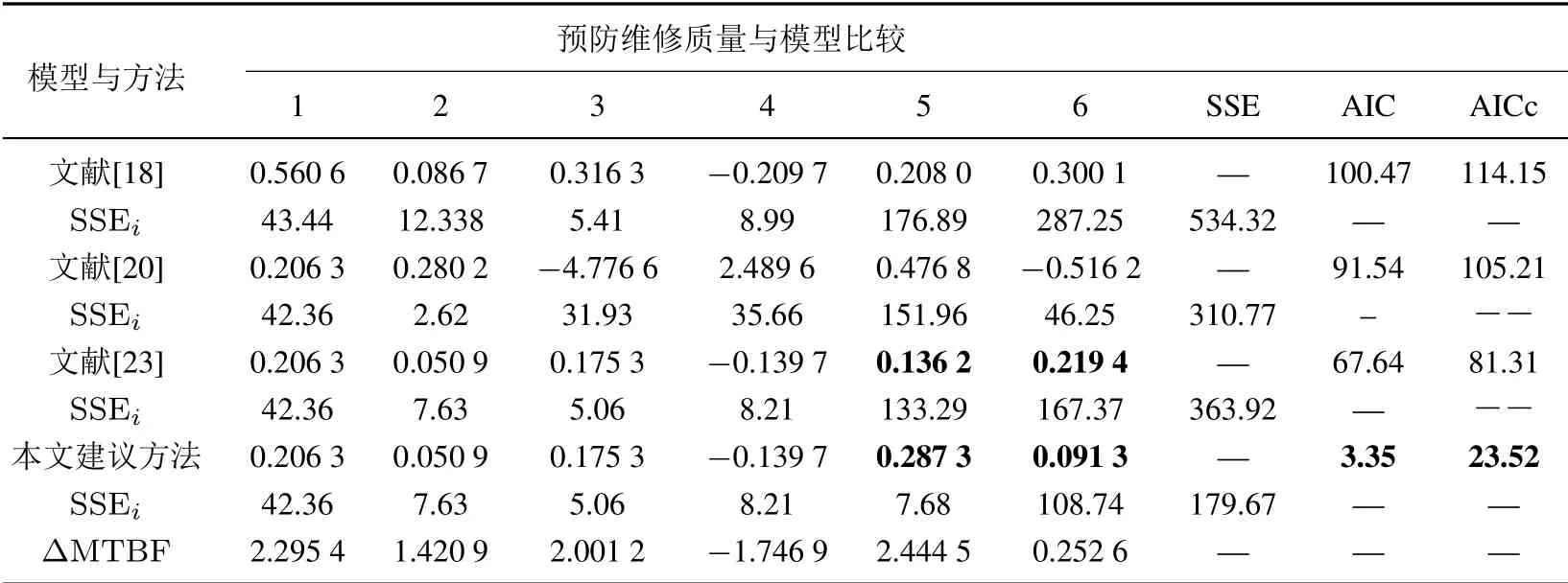
表3 建模结果Table 3 Modelling results

最终, 估计得到的预防维修质量如表3 所示.根据表3 所示的建模结果, 本文建议的模型具有最小的SSE 值,AIC 值和AICc 值,故本文建议的模型具有最优的拟合优度.为了进一步说明参考模型与本文建议模型对预防维修质量评估的有效性,根据2.3 节模型比较与验证中所描述的验证方法,通过原始数据计算得到了二级预防维修区间内的ΔMTBF,如表3 最后一行所示.

根据表3 中的评估结果,运用0-1 标准化方法, 将文献[18, 20, 23]和本文建议方法所得到的评估结果与ΔMTBF 进行对比, 比较结果如图3 所示.可见本文建议方法得到的预防维修质量变化曲线与实际的ΔMTBF 变化趋势非常一致.为了说明一致性程度,进一步应用欧式距离衡量了几种方法与ΔMTBF 的相近程度.经计算,文献[18,20,23]和本文建议方法与ΔMTBF 的欧式距离分别为0.427 3,1.969 5,0.378 1和0.148 1.本文建议方法与ΔMTBF 具有最相近的趋势变化,这进一步说明了本文方法的有效性.

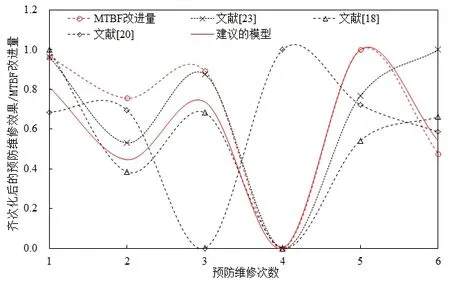
图3 模型比较Fig.3 Comparison between models

4 结束语

在算术失效强度减模型中,通常假设设备的失效强度平滑变化.然而,发现现实情况中设备失效强度的变化有可能存在变点.因此,本文在前期研究工作基础上,给出了一个具有失效变点的算术失效强度减模型.为了验证方法的有效性,本文给出了以预防维修区间内的MTBF 改进量的变化趋势为衡量依据,并以某巴士车辆的二级预防维修数据为例开展了案例研究.案例研究中,本文建议的建模方法与文献已有相似的模型进行了比较.研究结果表明,本文建议的变点-算术失效强度减模型不仅具有更优的模型拟合优度,而且还具有与MTBF 改进量最小的欧氏距离,这表明本文建议的方法是有效可行的.