数形结合思想方法在高中数学教学中的应用分析

廖警

摘 要：随着我国教育事业的不断发展，对于学生的综合能力也有了较高的要求。在高中数学学习过程中，数形结合思想运用得比较多，因此就要加强数形结合思想方法在高中数学教学中的应用，让学生能够通过数形结合思想方法更好地理解所学的数学知识并且在头脑中建立联系，为以后的高考以及更深入地学习数学打下坚实的基础。

关键词：数形结合;思想方法;高中数学;教学措施;应用分析

数学作为学生各个学习阶段都要学习的科目之一，在学生的学习生涯中占据着非常重要的地位。高中数学的学习比较抽象，学生不管是学习还是理解都存在一定的难度，对于学生的逻辑思维能力要求比较高。为了能够帮助学生更好地理解所学内容，加强学生数学思维的培养，教师就要重视数形结合思想方法在高中数学教学中的应用，让学生在头脑中自动将所学知识建立起联系，从而找出适合自己的解题方式;教师要将与之有关系的数学知识在合适的习题以及场景中加以利用，进一步加快学生的解题速度，同时更好地培养学生的问题解决能力。

一、高中数学教学中存在的问题

（一）学生无法及时对所学知识进行提取，影响解题思路

众所周知，在利用数形结合思想方法进行解题和学习时，会用到很多之前学习的内容，这就要求学生在熟练掌握所学习的数学知识的同时，还可以在解题时能够顺利提取出来，从而保证解题过程顺利和完整，能够给自己解题提供必要的帮助。但是在实际的问题解决中，由于学生没有将之前的知识掌握扎实，因此无法在短时间内提取知识，进而影响了自己的解题思路，解题效率也得不到提升。

（二）学生不愿意动脑

应用数形结合思想方法，要求学生在画图之后，通过图形整理自己的解题思路。要想将整个题目都顺利解决，学生需要先在头脑中建立相关的联系再进行图形的绘制。但实际上，很多学生没有将其价值充分明确，认为即使做出来了，得到的分数也不是很高，并且还会浪费自己很多的时间。这样导致学生不仅无法在要求的时间内完成相应的题目解答，还让他们的数学思维能力发展受到了限制，不利于学生的全面发展。

二、数形结合思想方法应用的意义

（一）有助于学生数学综合能力的提升

在高中数学学习过程中，学生通过解题可以在头脑中建立起数学知识间的联系，再加上数学学科涉及的内容比较复杂，涉及面很广，采用之前的数学学习方式已经无法满足学生实际的学习需求。通过利用数形结合思想方法，可以讓学生发现学习重点和难点，积极思考，通过寻找图形和题目的关系来解题。同时，学生在具体的学习中进行自主学习和自主谈论，其自主学习意识能够充分发挥出来，学习数学的积极性和主动性也能够得到较好的激发，加强了对学习内容的理解，从而有助于学生数学综合能力的提升。

（二）有助于学生数学探究意识的培育

数学本身的抽象性比较强，因此必须要培养学生能够独立发现问题及解决问题的能力，能够透过所学习的抽象内容看到本质，进而激发学生的数学探究意识。有效地培养学生的探究能力，其要求学生在做出相应的图形后，必须要思考才可以进行接下来的解题和学习，有效地锻炼了学生的思维能力和探究能力。另外，在学生计算的过程中，其数学运算能力还得到了培养，思维能力也得到了锻炼，从而有效地帮助学生提高数学成绩，最大限度地培育了学生的探究意识。

三、数形结合思想方法在高中数学教学中的应用

（一）在数学运算中加强数形结合思想的应用

高中数学教育的重点内容之一就是学生的计算能力，这也是教学的难点。通过数学运算的教学来加强对学生核心素养的培养，这是非常有效的措施。从目前的教学情况来看，很多学生能够将运算的公式和方法记住，但是却记不住原理，也就是说他们对知识的理解程度不够。这就需要教师在学生的运算过程中加强数形结合思想的渗透，让学生明白数和图之间的关系，给学生更直观的形象感受，从而让学生的运算能力得到有效提升，促进学生数学思维的锻炼。

（二）在实际解决问题的过程中利用数形结合思想方法

教师利用数形结合思想可以让学生将实际的数学问题和数学知识之间建立起一定的联系，在解决实际问题的过程中灵活运用所学习的知识，进而培养学生的数据分析能力和应用知识的能力。另外，还能让学生将数学知识和生活实际相联系，学生理解起来也比较轻松。在实际的教学中，教师要指导学生在图形中标出已知条件，然后再根据图形形进行综合分析，这样就能够有比较直观的感受，实际问题的分析解决提供了便利。

（三）在学生作业中充分利用数形结合思想方法

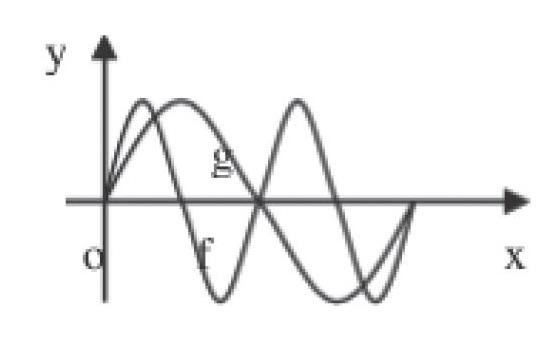
学生日常作业中利用数形结合思想方法也可以充分将自身优势发挥出来，不仅帮助教师了解学生本阶段的学习情况，还可以学生加强对该方法的应用。例如，在函数学习的过程中，可以要求几名学生对自己作业上的练习题进行计算和图象的说明，并通过图形的方式来表现出自己的整个解题过程。这样可以让学生对数形结合思想方法有更深刻的认识，加强对所学知识的理解，还可以有效提升学生计算的准确率。例如，教师布置的作业中有这样一道练习题：方程sin2x=sinx在区间（0，2π）解的个数是（ ）。这是一道典型的数形结合习题，在解题时可以作这样的图：

如上图，在同一坐标系内，作出y=sin2x，x∈（0，2π）;g=sinx，x∈（0，2π）的图有三个交点，所以方程sin2x=sinx在（0，2π）内有三个解。一般情况下，将方程式的一端为曲线，一端为动直线，解题较为简单，能够考查学生的逻辑思维能力与计算能力，还体现划归与转化和分类讨论的思想。学生可以简单快速地解决。

四、结语

综上所述，数形结合思想方法在高中数学教学中的应用对于学生的数学学习具有深远的影响，图形与题目相结合能够让学生对题目的理解更深刻，不仅加快了学生做题的速度和准确率，而且锻炼了学生的思维能力。另外，这种方法帮助学生将所学的数学知识更系统地保存在自己的记忆中，后期不管是更深入的学习还是理解知识，都可以及时利用，有效地提高解题的速度和准确性，促进自我综合能力的提升。

参考文献

[1]李金业.数形结合思想方法在高中数学教学与解题中的应用[C].教育部基础教育课程改革研究中心.2020年“基于核心素养的课堂教学改革”研讨会论文集，2020：1880-1882.

[2]邹宁.数形结合思想方法在高中数学教学与解题中的应用分析[C].中国智慧工程研究会智能学习与创新研究工作委员会.2019年教育信息化与教育技术创新学术论坛年会论文集.2019：637-639.

[3]雷鹏.数形结合思想方法在高中数学教学与解题中的应用[J].中国农村教育，2019（15）：118.