利用方位角信息的移动机器人编队控制
谭 瑶,梅 杰
(哈尔滨工业大学(深圳)机电工程与自动化学院,广东深圳 518055)
1 引言
近年来,随着人工智能技术的迅速发展,多智能体协同操作技术得到越来越广泛的应用.相比单智能体,多智能体系统工作能力大大提高,并且具有更强的鲁棒性和容错性[1].许多学者在多智能体系统方面也做了大量研究.文献[2]采用线性变换方法研究了通信不确定的多智能体系统的鲁棒一致性问题.Wang[3]等人对异构多智能体系统的一致性问题进行了研究.作为多智能体协同控制的一个重要领域,多智能体编队控制具有十分广泛的应用前景,比如无人机编队表演、智能物流、军事侦察等.
传统的编队控制的研究方法可分为以下几类:跟随领航者法、基于行为法、虚拟结构法以及基于图论法[4].跟随领航者法就是指定系统中某一智能体作为领航者,其余的智能体跟着领航者运动,这样就把编队控制问题转化为控制跟随者跟踪领航者的位置和方向的问题.Kumar教授带领的GRASP团队提出了两种跟随领航者的编队模型:基于距离–角度模型和基于距离–距离模型,并通过反馈线性化方法设计了稳定的控制算法[5].领航者的选择和编队队形的拓扑结构选择也是跟随领航者方法的一个研究重点.Ji等在文献[6]中指出跟随领航者编队方法的可控性由多智能体系统的拓扑图唯一决定.文献[7]将模糊控制算法应用于跟随领航者编队控制,设计出不依赖智能体模型的控制算法.基于行为法是通过设计并组合一系列基本行为来控制编队,它最早用于计算机动画中模拟动物群的聚集行为[8],随后Balch[9]将该方法应用到多智能体系统的编队控制中,并进行了仿真与实物的对比.Lawton[10]将基于行为法应用到空间飞行器的编队控制中.虚拟结构法是把多智能体系统的队形看作虚拟的刚性结构,各智能体通过跟踪虚拟点实现编队.Ren[11]等引入反馈控制克服智能体编队运行时扰动对队形控制的影响.基于图论法主要是借助图论的一些特殊性质设计控制算法,如利用图的拉普拉斯矩阵的特征值分布来分析控制算法的稳定性[12].在上述研究中,所设计的控制算法都使用了相对位置(或距离)信息,而实际中距离信息比较难以精确获得甚至无法获得.
为克服实际中距离信息难以精确获得的问题,新近出现的基于方位角信息的编队控制研究受到越来越多的关注.在基于方位角信息的编队控制研究中,编队的理想队形是由各智能体间的方位角约束决定的,不必考虑各智能体间的距离问题,控制算法的设计也不需要用到距离信息.Meysam[13]等提出基于智能体的角度信息的控制算法,使得多智能体系统形成三角形队形,但该算法只能形成三角形队形.Adrian[14–15]提出了一种仅利用智能体间方位角信息的编队控制算法,最后通过庞加莱–本迪克松定理(Poincare-Bendixson Theorem)证明了控制算法的全局稳定性,但该算法仅仅适用于涉及3个或4个智能体的场景.为了实现大规模的编队控制,Zhao[16]等人借助最小方位刚性图理论提出一种新的控制算法,分别对一阶积分器模型和二阶积分器模型以及非完整动力学模型进行编队控制,最终证明其控制算法的稳定性,但对于非完整约束动力学模型的编队控制无法实现队形的缩放控制,队形的整体规模由智能体的初始状态决定.
结合前面的研究结果,本文在智能体模型为非完整动力学模型的情形下利用智能体间的方位角信息进行编队控制算法设计,并在最后通过仿真实验来验证研究结论.与现有的编队控制算法相比,本文仅使用方位角信息,不直接使用任何距离信息,使得控制算法在实际中更容易实现.与文献[14–15]相比,本文利用李雅普诺夫稳定性理论证明系统的稳定性,对智能体的个数没有限制,可实现大规模的编队控制.相比文献[16],本文可实现整体队形的缩放控制.
2 数学背景与问题描述
首先介绍本文用到的移动机器人模型、刚性图理论以及控制目标.
2.1 移动机器人模型
本文中所采用的移动机器人模型如下[17]:

上式中:pi=[xi yi]T表示移动机器人i两轮中心与轴线的交点的位置坐标,vi和wi分别表示移动机器人的线速度和角速度,θi表示移动机器人的前进方向与全局坐标的x轴的夹角,如图1所示.本文的控制目标就是设计控制算法[vi wi]T使得移动机器人系统形成目标队形.
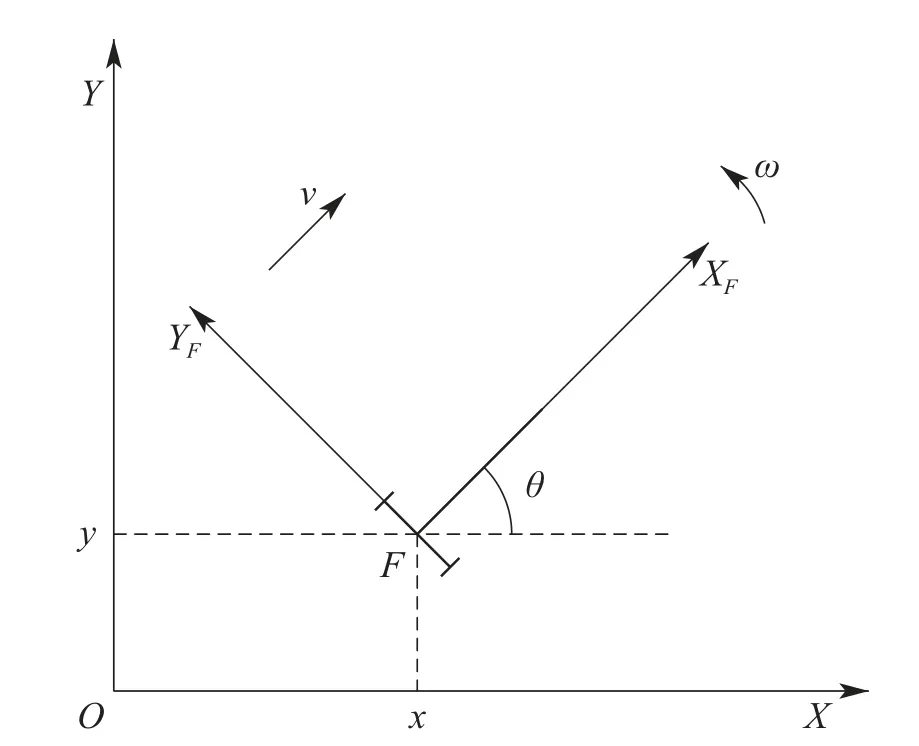
图1 移动机器人模型Fig.1 The model of mobile robot
2.2 刚性图理论
本文只讨论二维空间的刚性图理论.在多智能体系统中,每一个智能体可看作一个节点,智能体间的约束看作节点与节点之间的边,用有向图G=(V,E)表示,其中V={1,2,···,n}为图中的顶点集,E为边的集合.本文中把边(i,j)∈E看作智能体i与智能体j间的方位角gij,其数学表达式为,其中eij=pj −pi.该方位角在实际中是可测的.那么可定义一个框架(G,p)代表编队队形,p表示智能体的位置坐标.为了使得编队队形唯一,需要给出合理的理想方位角约束.Leonard[18–19]等人表示,在二维空间中,如果队形框架的顶点数n和边数m满足m=2n −3,那么该队形框架形状唯一(在不考虑缩放情况的前提下).对于有向图的关联矩阵H=[Hki]∈Rm×n,当顶点i是边k的起点时,[H]ki=−1,当顶点i是边k的终点时,[H]ki=1;若顶点i不在边k上,则[H]ki=0.
定义向量e表示由m条边对应的eij所组成的列向量,p=[p1p2··· pn]T表示由n个智能体位置组成的列向量,则,其中=H ⊗Id[20].
这里,基于智能体间的方位角,引入如下非常重要的辅助量–正交投影矩阵:
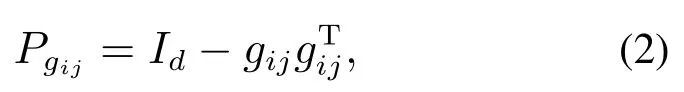
其中Id ∈R2是一个二维的单位矩阵.不难发现,Pgij是半正定的,且对任意与gij平行的向量x都有Pgijx=0成立.
2.3 控制目标
本文的控制目标:基于由式(1)表示的非完整约束移动机器人系统,在领航者运动状态已知的前提下,仅使用智能体间的方位角信息,分别为第1跟随者和其余跟随者设计控制算法[vi wi]T,使得各智能体间的方位收敛至给定的期望值,且所有智能体的速度和航向角都收敛于领航者的速度和航向角,这也就意味着整个移动机器人系统将保持特定的队形进行整体运动.
3 控制算法设计
3.1 位置估计控制算法设计
为了克服实际中相对位置信息无法直接获得的难点,本文设计一个基于方位角信息的位置估计算法来获得准确的相对位置信息.在全局坐标系O中,领航者和跟随者的相对位置为plf=pl −pf,那么在跟随者的局部坐标系F中,两者的相对位置为
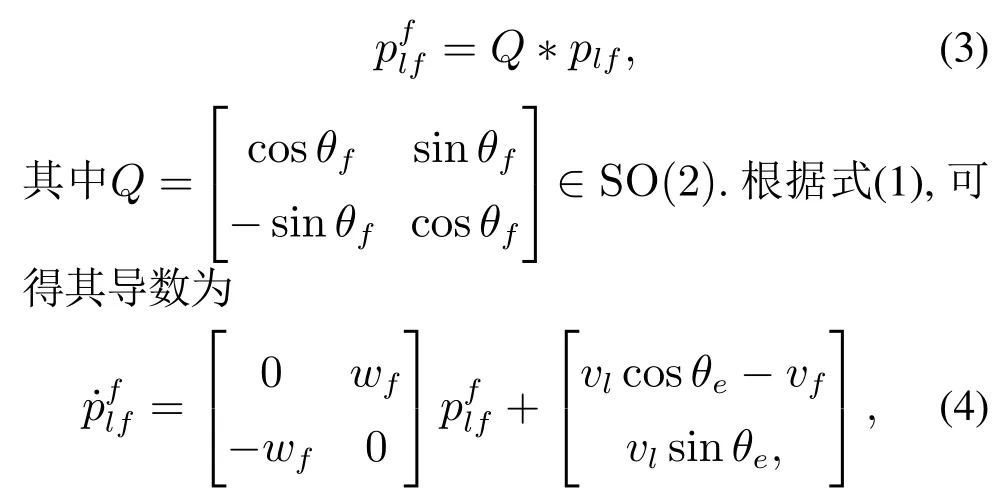
其中:θe=θl −θf,下标l表示领航者的相关量,下标f表示跟随者的相关量.仅使用方位信息,设计如下位置估计算法:

引理1在领航者速度信息已知的前提下,算法(5)能估计出准确的位置信息,且估计误差−plf将最终收敛于零.

3.2 第1跟随者控制算法设计


假设1领航者的线速度和角速度是有界的,且线速度是一致连续的.
对第1跟随者,设计如下控制算法:
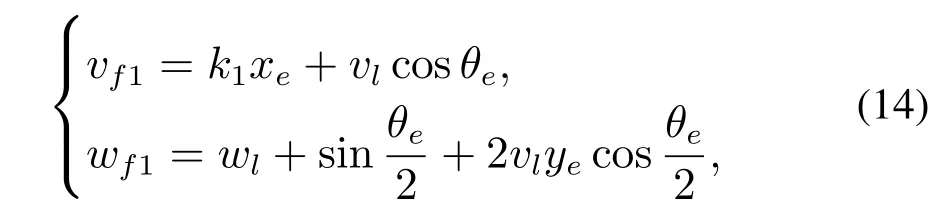
其中:k1为任意大于零的常数,θe是可测的,xe,ye为第2.1节估计的相对位置信息.最后,得到如下结论.
定理1在假设1成立的前提下,跟踪误差(12)在控制算法(14)作用下将收敛到理想值,且线速度和角速度也最终分别收敛于vl和wl.

3.3 编队控制算法设计
本文中,除了领航者和第1跟随者以外,剩下的均为其余跟随者,它们通过与邻居智能体间的方位约束决定了整个队形框架,所以应选择合适的方位约束,使得队形框架唯一,队形的缩放由领航者和第1跟随者决定.在这里,控制算法的设计要用到第1.2节中提到的正交投影矩阵,通过该矩阵约束智能体间的方位.把作为控制算法的重要组成部分,它的几何解释如图2.
其中hi=[cosθisinθi]T,那么,
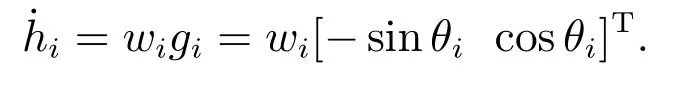
编队控制算法如下:

结合第2.1节提出的位置估计控制算法和第2.2节提出的第1跟随者跟踪控制算法,对于移动机器人系统的主从式编队控制,得出以下结论.
定理2在主从编队(G,p)控制系统中,领航者以固定速度自由运动,在仅利用智能体间的方位信息设计的第1跟随者控制算法(14)和编队控制算法(25)作用下,第1跟随者与领航者之间保持期望的相对位置,所有智能体间保持期望的方位约束,整个系统以共同速度运动.
证令p=[p1p2··· pn]T,h=[h1h2···hn]T.p1,p2分别为领航者和第1跟随者的位置信息.把式(25)代入式(24)中,可得
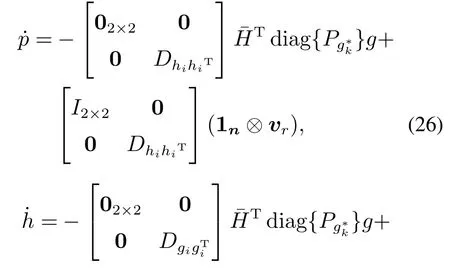
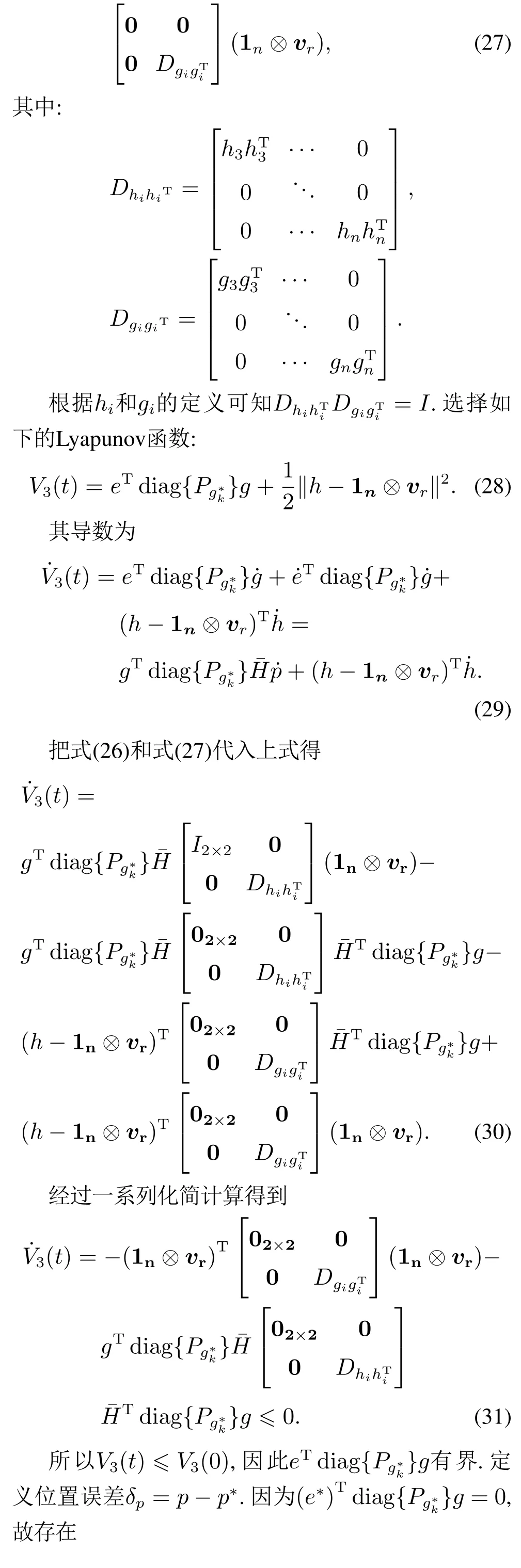

4 仿真分析
在本小节中,通过仿真来验证所设计的控制算法的有效性.考虑由5个移动机器人所组成的系统,所有移动机器人的动力学均为相同的非完整约束动力模型.本文的目标队形为一个正五边形,各智能体间的目标方位约束如下:
设定领航者的线速度为v1=0.1 m/s,角速度为ω1=0 rad/s,运行角度为θ1=+90◦.
缩放因子α可根据需要进行选择.本小节选择了两个不同大小的缩放因子,当t<190 s时,令α=1;当t≥190 s时,令α=2;由此实现目标队形的缩放控制,即目标队形由一个边长为1 m的正五边形扩大为一个边长为2 m的正五边形.
图3表示各移动机器人的运动轨迹以及最终形成的目标队形.由图可知,随着缩放因子α的变化,整个移动机器人系统的目标队形也会发生对应的变化并最终达到稳定状态,这也体现了本文提出的算法相比于现有算法的一个优势.由图4可以看出各移动机器人间的实际方位角与期望方位角之间的误差收敛于零;并且由图5可以看出各个移动机器人的线速度和角速度也分别收敛于领航者的线速度和角速度.综上所述可知,整个多移动机器人系统在所设计的控制算法的作用下能够实现本文的编队要求,这也验证了本文所提出算法的有效性.
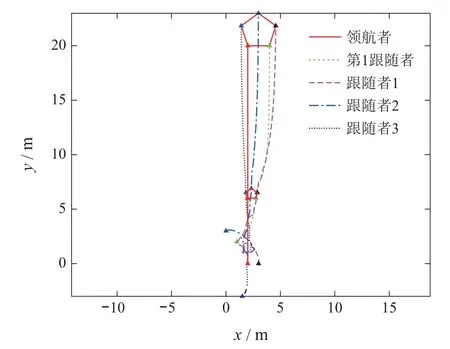
图3 智能体运动轨迹和最终队形Fig.3 The trajectories and final formation
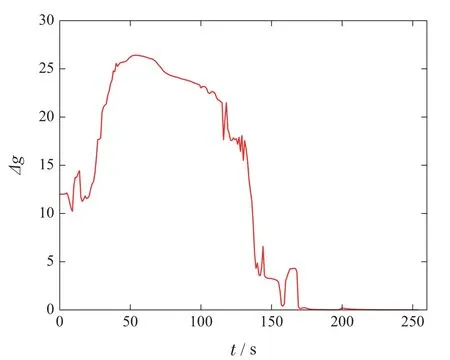
图4 方位角总误差Fig.4 Total bearing error
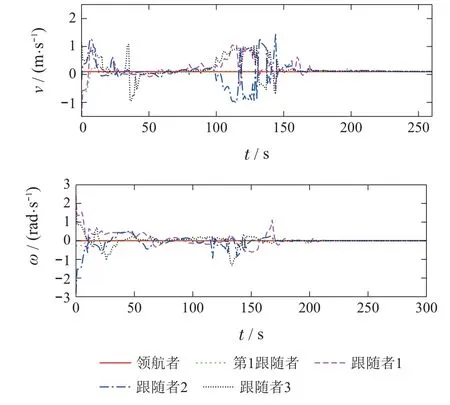
图5 智能体线速度、角速度Fig.5 Linear velocity and angular velocity of each agent
5 ROS实物实验
为了验证本文提出的编队控制算法在实际场景中应用的可行性,本部分将在Gazebo环境中选取Turtle-Bot3移动机器人进行验证.各机器人的初始状态和目标方位约束均与第3节中相同.
图6 表示的是在Gazebo 仿真环境中各个Turtle-Bot3的运动轨迹,可以明显地看出,多TurtleBot3移动机器人系统可以形成期望的编队队形并且能够保持该队形的同时进行运动;图7表示的是各TurtleBot3实际方位角与期望方位角间的误差变化曲线,最终该误差收敛到零,满足编队要求;图8表示的是各个Turtle-Bot3的线速度和角速度变化曲线,从图中可以看出所有的TurtleBot3的线速度和角速度均收敛于领航者的线速度和角速度,其中速度与第3节中不同是因为在Gazebo环境中TurtleBot3限速为0.26 m/s.综上分析可知,实物实验结果与数值仿真结果一致,所以本文提出的编队控制算法在实际场景中具有一定的可行性.
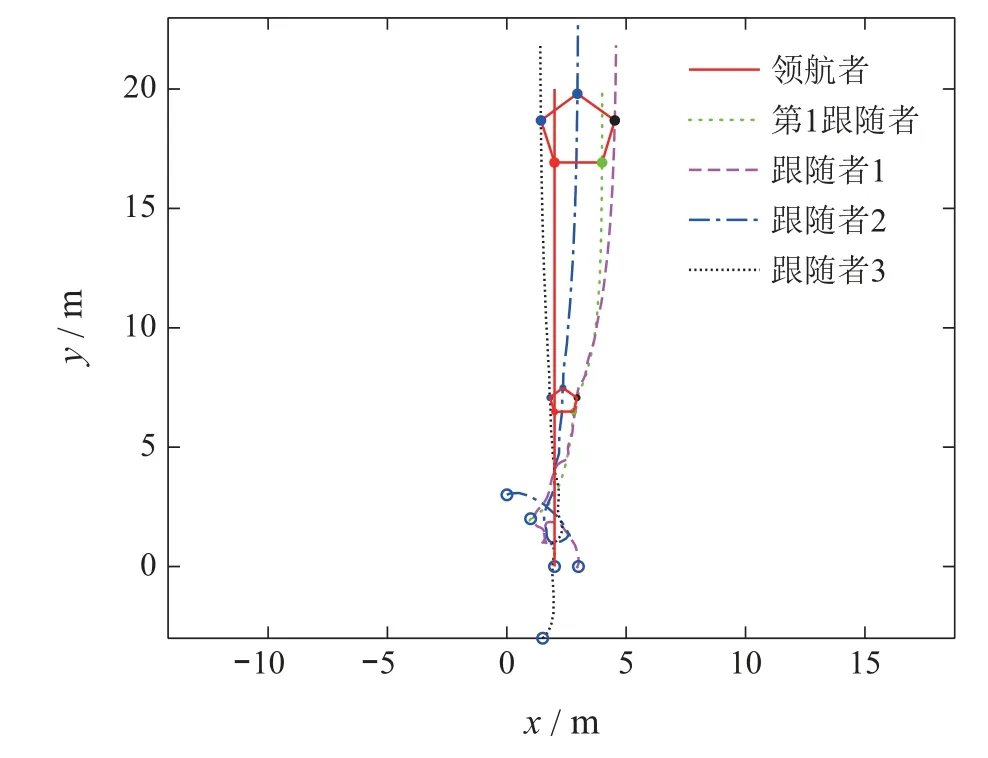
图6 各个TurtleBot3运动轨迹和最终队形Fig.6 The trajectories and final formation of TurtleBot3
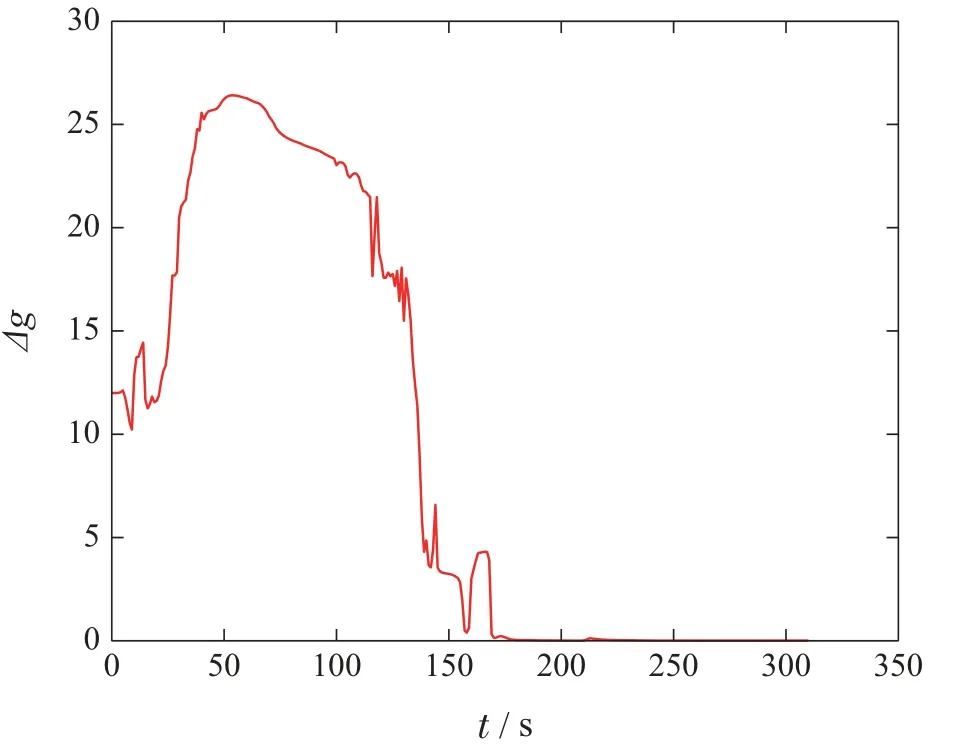
图7 方位角总误差Fig.7 Total bearing error

图8 各个TurtleBot3线速度、角速度Fig.8 Linear velocity and angular velocity of TurtleBot3
6 结论
本文主要基于方位角信息研究多移动机器人系统的编队问题.通过智能体间的方位约束构建整体队形框架,同时,通过控制第1跟随者与领航者间的相对位置来实现整体队形的缩放.此外,还引入辅助变量设计位置估计算法以克服实际中位置信息无法准确获得的问题.在所设计的控制算法的作用下,整个系统达到目标队形并以固定的速度进行运动.最后通过数值仿真和ROS实物实验验证了算法的有效性.
—— 瓮福集团PPA项目成为搅动市场的“鲶鱼”

