基于super-twisting算法的多航天器姿态有限时间分布式协同控制
许 淼方一鸣 李建雄 赵晓东
(1.燕山大学工业计算机控制工程河北省重点实验室,河北秦皇岛 066004;2.燕山大学智能控制系统与智能装备教育部工程研究中心,河北秦皇岛 066004)
1 引言
与传统大型航天器相比,一组小而经济的航天器具有更高的灵活性、更强的鲁棒性和更低的成本[1–4].由于分布式合成孔径雷达、三维立体成像等多航天器对地观测任务需要各航天器指向地球上的特定位置,这就必须保证各航天器能跟踪上预设的姿态轨迹[5].因此,多航天器协同控制技术作为对大型航天器技术的必要扩展和补充,具有重要的研究价值.
滑模控制作为一种特殊的非线性控制,被应用于多航天器姿态协同控制[6–8].滑模面可以独立于参数和干扰进行设计,因此滑模控制具有响应速度快、对参数变化和干扰不敏感、物理实现简单等优点.然而,传统的滑模控制会产生影响系统性能的抖振.文献[9]用“sigmoid”或者饱和函数代替不连续控制项来抑制抖振.然而,这种近似控制是以牺牲系统的性能为代价.文献[10–11]提出的super-twisting算法是一种典型的二阶滑模控制算法,该算法在保持传统滑模鲁棒性的同时,可以提高系统的精度,削弱抖振的影响.文献[12]基于齐次性方法设计了一个有限时间supertwisting 控制器,但不能计算系统的收敛时间.文献[13]将Lyapunov方法应用于不确定系统的super-twisting算法的性能分析,克服了收敛时间无法计算的问题.文献[14]提出一种无模型自适应分数阶supertwisting滑模控制来实现机器人在不确定性和外部干扰下的轨迹跟踪问题.文献[15]针对一类带有非匹配干扰的非线性系统,设计一种自适应super-twisting滑模控制器,提高了系统的鲁棒性.文献[16]将supertwisting滑模与模糊系统相结合,设计了一种鲁棒控制器,利用super-twisting滑模的概念来削弱抖振问题.
上述研究都是基于单输入单输出系统,不适用于多输入多输出系统.文献[17–19]针对带有未知干扰和不确定性的多机器人系统编队控制问题,基于领导–跟随结构,设计了super-twisting滑模控制器.在所设计的控制器下,系统领导–跟随误差可以在有限时间内收敛.文献[20]针对多机器人协调控制问题,提出了一种新的super-twisting神经网络及其外部干扰抑制模型,以提高协调控制的有限时间收敛性和对外界干扰的鲁棒性.上述文献中,每个航天器的控制器设计都是基于各自的领导–跟随误差,并未考虑与邻居的交互信息.并且当领导者与第i个跟随者之间没有信息交互时,该控制器的设计方法将不再适用.为了实现具有双积分动力学的多智能体系统有限时间编队控制和目标跟踪,基于多输入多输出super-twisting算法,文献[21]提出了一种由观测器和非光滑反馈控制律组成的算法.在所设计的控制器下,系统状态在有限时间内快速收敛.然而,控制器设计是集中式的,集中控制方式的系统结构较为简单,但由于控制器设计时需要系统的全局变量,因此,对系统的通讯要求较高.
此外,实际航天器系统中通常存在多种影响因素,包括由重力和太阳辐射等外作用力产生的干扰力矩以及执行器故障等.这些干扰和故障会对系统性能产生影响.针对带有外部干扰的一组航天器,文献[28]提出了一种分布式自适应姿态协同控制方案,由于采用有限时间控制方法,提高了系统的响应速度.本文针对存在外界干扰和执行器故障的多航天器姿态分布式协同控制问题,设计了基于多航天器姿态一致性误差的super-twisting分布式协同控制器.首先,对每个航天器设计有限时间自适应滑模干扰观测器来估计系统外界干扰和执行器故障构成的集总干扰.其次,将积分滑模与super-twisting算法相结合,提出一种分布式协同控制器.由于所设计的控制器不需要包含系统的全局信息,因此该控制器可以实现分布式控制.再次,利用Lyapunov稳定性理论证明了多航天器姿态可以在有限时间内收敛到平衡点附近的邻域内.最后,仿真及对比结果表明,本文所提出的分布式控制器具有更快的收敛速度和更高的控制精度.
2 系统描述与控制问题提出
2.1 符号定义
给定向量x=[x1x2··· xn]T及常数α>0,定义sigα(x)=[|x1|αsgnx1|x2|αsgnx2··· |xn|αsgnxn]T,其中sgn(·)为符号函数.对于向量q=[q1q2q3]T,定义向量q的反对称矩阵q×为
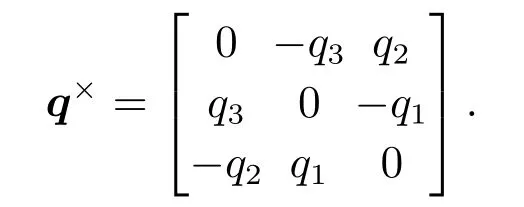
2.2 引理及定义
引理1[29]若在包含原点的邻域Ω(Ω ⊂Rn)内,存在连续可微函数V(x)和实数l0>0,ϑ>0,µ∈(0,1),对于满足

V(x0)为V(x)的初始值,0<ρ≤1,0<ρ0<1.
引理2[23]若在包含原点的邻域U(U ⊂Rn)内,存在连续可微函数V(x,t)和实数l1>0,l2>0,θ ∈(0,1),ξ >0,对于满足:

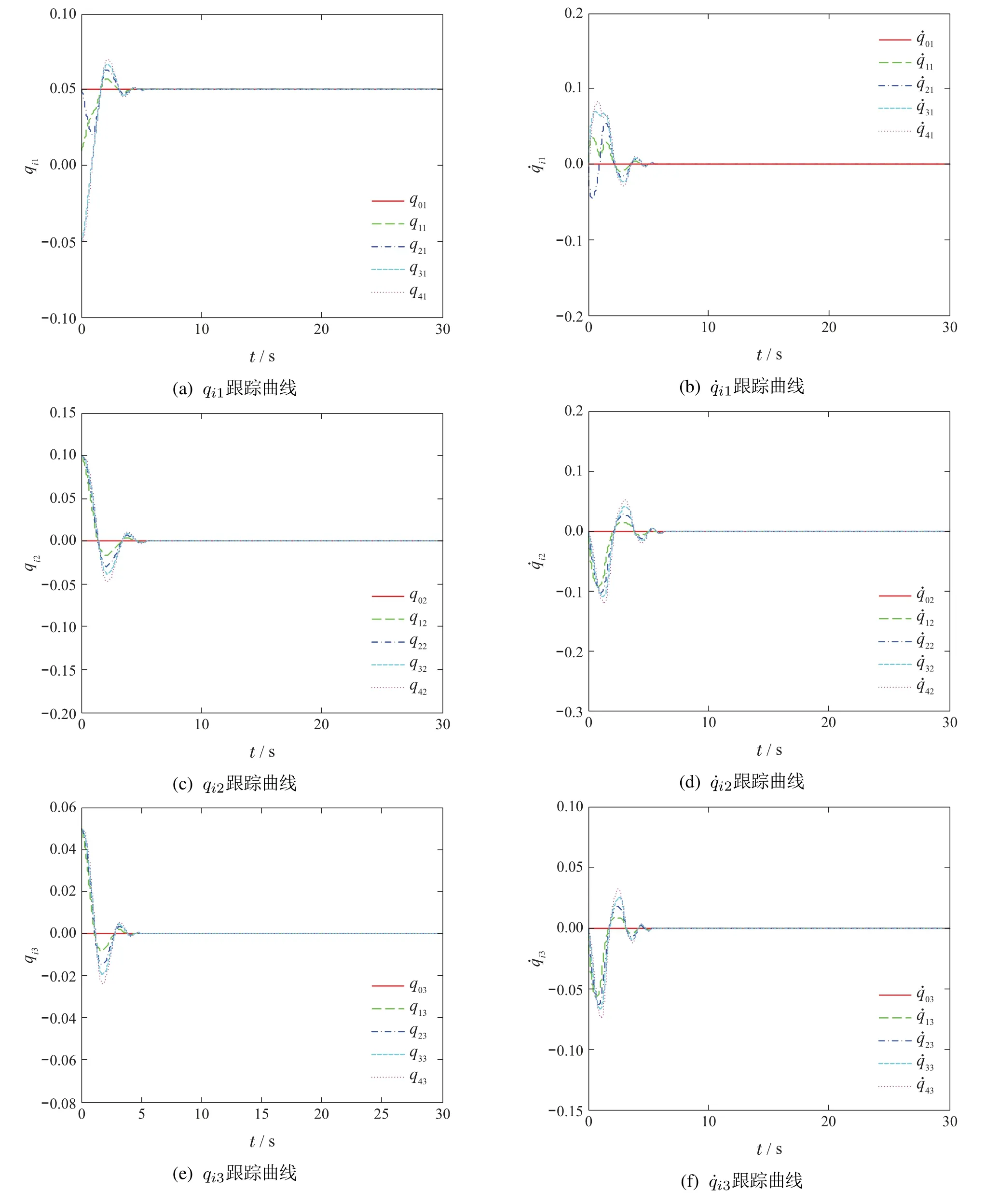
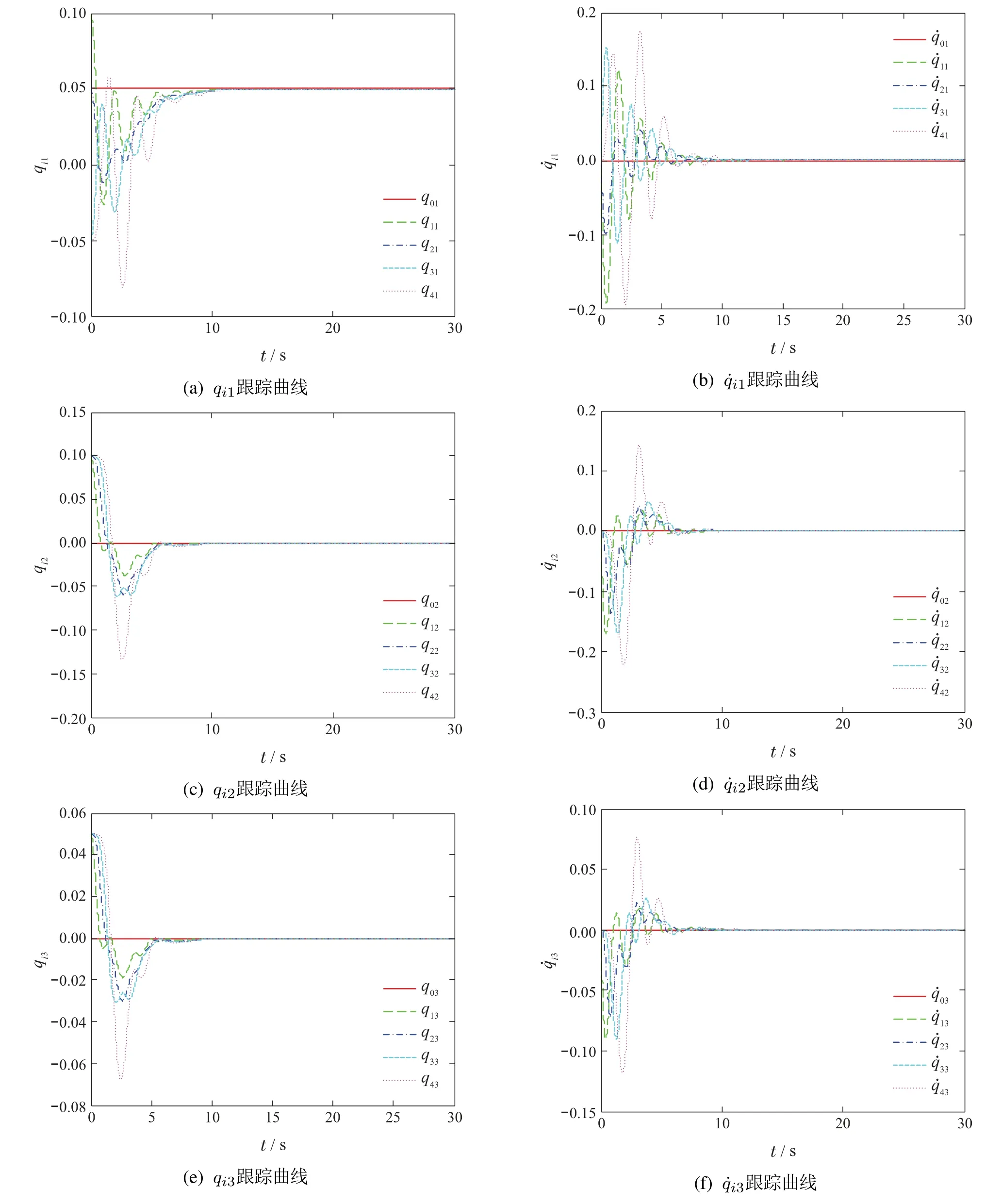
V(x0,0)为V(x,t)的初始值,0<κ 引理3[24]对于任意正实数m,n,w和实数变量φ和ψ,有如下不等式 本文采用修正的Rodrigues参数(MPRs)[26]来描述各航天器的刚体姿态运动.第i(i=1,2,···,n)个航天器的动力学方程如下 根据文献[26],得到Euler-Lagrange形式的多航天器运动学方程如下 由性质1可知,Mi(qi)有界.根据di的定义,假设2是合理的. 本文的主要目的是设计分布式协同控制器uci(i=1,2,···,n),使得多航天器的姿态在具有外界干扰及执行器故障的情况下,在有限时间内快速跟踪参考轨迹. 为了估计系统的集总干扰di,本文使用了一个自适应滑模干扰观测器. 定义一个滑模面 定理1在假设2下,针对第i个航天器系统(6),在所设计的滑模干扰观测器(8)及自适应律(9)下,观测误差可以在有限时间内收敛到平衡点附近的邻域内. 根据引理1,观测误差可以在有限时间收敛到平衡点附近的邻域内. 定义一致性误差 可以在有限时间内有界稳定.由于χ2可以在有限时间内有界稳定,故状态χ1也可以在有限时间内有界稳定.即:多航天器的姿态可以在有限时间内收敛到平衡点附近的邻域内. 注1将文献[22]中的滑模面 将第1项中的χi,2变为xi,2,可以避免在控制器设计时引入全局的拉普拉斯矩阵H,从而实现了分布式控制.即:当领导航天器与第i个航天器有信息交互时,第i个航天器仅根据自身信息、邻居航天器的信息及领导航天器信息进行姿态调整.当领导航天器与第i个航天器没有信息交互时,第i个航天器仅根据自身信息及邻居航天器的信息进行姿态调整.与集中式控制器相比,本文所设计的分布式控制器仅采用自身信息及邻居航天器信息,具有更低的通讯要求和更高的灵活性. 注2由于引入super-twisting算法,加快了系统的收敛速度.控制器设计包含快速趋近律和指数趋近律Si两部分.当系统状态离滑模面较远时,指数趋近项Si保证系统的快速收敛.当系统状态离滑模面较近时,快速趋近项保证系统的快速收敛. 为了验证本文所提方法的有效性,针对1个虚拟领导者和4个跟随者的多航天器模型,将本文所提方法与文献[28]方法进行仿真对比研究. 4个跟随者的惯性矩阵为 虚拟领导者的姿态为q0=[0.5 0 0]T.系统的外部干扰为 执行器故障的效率因子为 偏差故障为 其中ϖ ∈[−1,1]为一个随机数. 自适应滑模干扰观测器参数选取ri=0.05,γi=0.5,ηi=0.1,ℓi,1=0.2. 控制器参数选取 图1为多航天器的通讯拓扑图.图2为有限时间姿态跟踪曲线.qij和为第i个航天器的第j个姿态及其导数.图2(a)–2(b)表示4个航天器姿态及其导数的第1个状态.图2(c)–2(d)表示4个航天器姿态及其导数的第2个状态.图2(e)–2(f)表示4个航天器姿态及其导数的第3个状态.图3表示了式(8)所示的系统在文献[28]提出的控制器下4个航天器姿态及其导数的有限时间跟踪曲线.从图2和图3(a)–3(b)等可以看出多航天器的姿态可以在有限时间收敛到达稳定状态. 图1 多航天器通讯拓扑结构图Fig.1 Communication topology of multi spacecraft 图2 本文控制器下的多航天器姿态及其导数跟踪曲线Fig.2 Multi spacecraft attitude and its derivative tracking curve under this paper 将图2和图3做对比可以看出,本文提出的控制器具有更快的瞬态响应和更强的鲁棒性.在本文提出的控制器下,4个航天器姿态在5秒左右到达稳定;而在文献[28]提出的控制器下,4个航天器姿态在10 s左右到达稳定.在文献[28]提出的控制器下要达到稳定状态还需要多5 s的时间.与文献[28]所设计的分布式有限时间姿态协同控制器相比,由于引入了super-twisting算法,本文提出的有限时间分布式协同控制器具有更快的收敛速度.从图2和图3对比可以看出,本文所提出的控制器具有更高的控制精度. 图3 文献[28]控制器下的多航天器姿态及其导数跟踪曲线Fig.3 Multi spacecraft attitude and its derivative tracking curve under reference[28] 本文研究了基于super-twisting算法和自适应滑模干扰观测器的多航天器姿态协同控制问题.首先,通过对每个航天器构造自适应滑模干扰观测器来估计系统外界干扰及执行器故障构成的集总干扰;然后,基于多航天器姿态的一致性误差将super-twisting算法与积分滑模控制相结合设计了分布式协同控制器,有效地避免了控制器设计中全局信息的引入,实现了分布式控制,简化了控制器的设计过程;最后,通过Lyapunov稳定性理论证明了多航天器姿态可以在有限时间内收敛到平衡点附近的邻域内.通过仿真及对比,结果表明:本文所设计的控制器具有更快的收敛速度和更高的控制精度.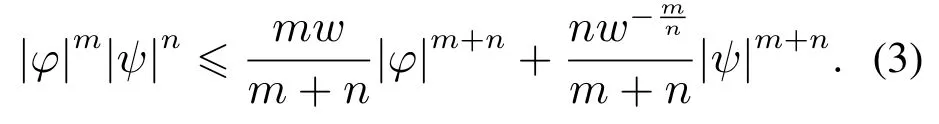
2.3 通讯拓扑

2.4 系统描述


3 自适应滑模干扰观测器设计


4 基于super-twisting和积分滑模面的分布式协同控制器设计




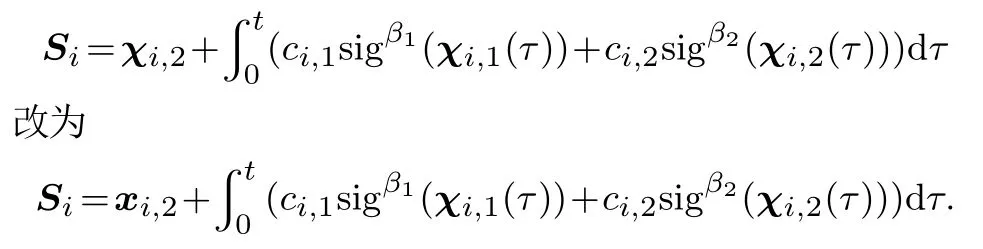
5 仿真研究
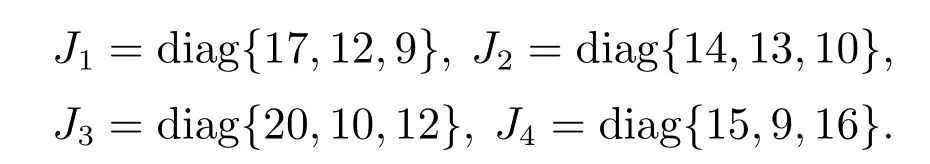
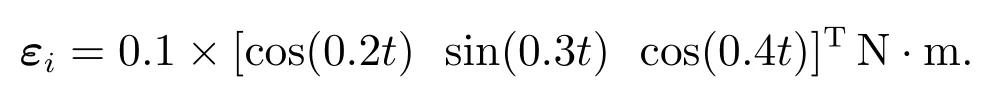


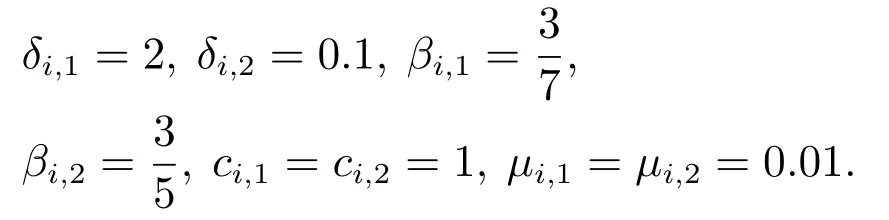

6 结论

