多无人水面艇协同海上溢油羽流监测
王俊伟,姚余磊
(北京科技大学自动化学院,北京 100083)
1 引言
海上溢油是一种高污染、难治理的突发环境污染事故.近年来,海上溢油事故频发,如美国墨西哥湾原油泄漏事件、巴西原油污染事件、蓬莱19–3油田溢油事故、“桑吉轮”碰撞溢油事故等,对海洋尤其是近海生态系统造成了极大破坏[1].海上溢油应急响应的主要任务之一是实时掌握溢油羽流输移动态,这需要对海上溢油进行大范围持续监测.传感器、海洋机器人、无线传输和机械系统控制等技术进步使得利用搭载化学传感器的移动海洋机器人网络大范围持续监测海洋环境成为可能[2],进而派生出多机器人协同海洋环境监测问题.现有成熟的多智能体协同控制理论不能直接解决上述海洋环境监测问题,因其大都忽略了环境的动态特性.因此,面向动态环境大范围持续监测的多机器人协同控制问题不仅具有重要的实际应用价值,还将进一步推动多智能体协同控制理论研究的发展.
目前,已有大量研究工作专注于多机器人协同动态环境监测问题[3–12].针对动态环境边界跟踪与合围,文献[4]为移动传感器网络开发一种包括随机覆盖控制、避碰控制和bang-bang角速度控制在内的协同控制算法.在文献[6]中,一种协同控制算法被提出用于驱动移动传感器网络跟踪环境边界的动态扩张.考虑到环境场时空动态可建模为由偏微分方程(partial differential equation,PDE)描述的分布参数系统[7],文献[8]利用飞行器测量的浓度数据提出一种基于Lyapunov的龙贝格型PDE观测器设计实现移动气体源的气体扩散浓度估计,其中气体扩散模型是由具有可变涡流扩散率和环境风的空间二维对流–扩散方程刻画.假设海洋机器人局部位置处的污染羽流浓度、梯度、散度信息均可得,学术专著[9]的作者为多机器人协同动态羽流边界跟踪与监测问题构造了一种基于模型的协同控制算法,其中羽流被建模为空间二维对流–扩散PDE.在作者前期研究工作[10]中,仅利用机器人局部位置处羽流浓度信息,从估计与控制角度出发,提出一种基于PDE观测器的控制策略用于解决单海洋机器人动态羽流边界跟踪与监视问题.具体来说,通过构造龙贝格型PDE观测器实现整个空间区域内动态羽流场估计,然后根据观测器方程设计运动控制算法引导海洋机器人跟踪动态羽流边界并在此边界上按给定速度巡逻.此思路被进一步推广到仅有点式浓度测量的双海洋机器人协同动态羽流边界跟踪与监测问题[11]和仅有局部区域浓度测量的多海洋机器人无领导者协同动态羽流边界跟踪和合围问题[12].需要强调的是上述协同控制算法设计均忽视了羽流模型误差和测量干扰的影响.另外,基于领导–跟随结构的多海洋机器人协同动态羽流边界跟踪和合围问题依然保持开放.
在前期研究工作[10–12]基础上,本文采用领导–跟随–锚结构进一步探讨海上溢油污染羽流多海洋机器人协同监测问题,其中溢油羽流的动态扩张是由含有过程干扰的二维空间对流–扩散机理模型刻画,且羽流边界是由事先设定阈值的水平集合刻画.本文致力于开发基于模型的协同控制设计方法使得n艘水面无人艇有效监测羽流边界的动态扩张.为此,在n艘水面无人艇中,选择两艘无人艇分别将其设定为边界领导艇和边界锚艇,其余艇设定为跟随艇.利用各自艇载化学浓度传感器测量的局部溢油羽流浓度信息,分别为边界领导艇、跟随艇以及边界锚艇构造基于分布一致龙贝格型PDE观测器控制策略.结合Lyapunov技术、集合稳定以及多智能体一致性理论,严格证明了所提出协同控制算法能驱动所有水面无人艇跟踪羽流边界的动态扩张并同时在此边界上形成均匀分布.最后数值仿真实验结果说明了所提出协同控制算法的有效性.

2 问题描述与前期准备
2.1 海面溢油污染羽流模型
海面溢油羽流动态扩散过程可由如下二维空间对流–扩散方程描述[10,12]:

受约束于齐次狄利克雷边界条件

和初始条件

假设1[10–12]假设海面洋流场v(x,t)是完全已知的且其散度∇·v(x,t)为零,即∇·v(x,t)=0.
2.2 无人水面艇数学模型
考虑由n艘无人水面艇构成的同构型海洋机器人网络,其无人艇运动学模型可由如下方程刻画[9]

其中:(x1(t),x2(t),θ(t))是无人水面艇在其笛卡尔坐标系下位置和航向;τ1(t)和τ2(t)是无人艇的控制输入.为获得一个更适用于控制设计的运动学模型,引入如下坐标变换[13]

当lc>0为已知常数时,欠驱动模型(4)可改写为如下单重积分器模型:

在同构型海洋机器人网络中,所有无人水面艇均配置相同的定位传感器、溢油羽流浓度传感器和无线通信模块.通过这些艇载设备,每艘艇均能获得其准确位置信息xr(t)和以xr(t)为中心的局部区域平均浓度测量,并与通信拓扑邻居节点交互信息.溢油羽流浓度y(xr(t),t)的表达式为

其中U(xr(t))是以xr(t)为中心的局部区域,其勒贝格测度为l(U(xr(t))),ω(t)是测量干扰满足|ω(t)|<ωm,ωm是事先给定常数.此测量方程可写成

若x ∈U(xr(t)),则χ(x,xr(t))=1,否则χ(x,xr(t))=0.不失一般性,假设l(U(xr(t))是一个常数,也就是说,l(U(xr(t)))是一个独立于艇位置xr(t)的参数.
2.3 控制目标与问题描述
为保证同构型海洋机器人网络有效监视溢油羽流的动态扩张过程,本文设定以下两个控制目标.第1个目标是驱动所有水面无人艇运动到由集合LS(C,Cf)≜{xf(t)∈R2|C(xf,t)=Cf}刻画的羽流边界,Cf>0是羽流边界的浓度阈值.第2个目标是n艘无人水面艇在羽流边界上形成均匀分布.
针对上述两个控制目标,本文拟讨论的控制问题正式定义如下.
协同动态羽流监测问题:针对由二维空间对流–扩散模型(1)–(3)描述的溢油污染羽流时空动态扩散过程,本文为由n艘无人水面艇构成的同构型海洋机器人网络开发协同控制算法使得:随着时间演化,受运动学模型(6)约束的n艘无人水面艇在‖xr(t)‖LS(C,Cf)范数意义下跟踪羽流边界LS(C,Cf),同时在此羽流边界上实现均匀分布.
为此,针对羽流场C(x,t),令

为无人艇位置xr(t)与由集合LS(C,CB)≜{xB(t)∈R2|C(xB,t)=CB}刻画的轮廓线之间的距离,其中常数值CB为事先给定的轮廓线值.本文引入如下关于无穷维集合LS(C,CB)的集合稳定概念.
定义1[10,12]受运动学方程(6)约束的无人艇是关于集合LS(C,CB)集合稳定,如果对任意时间td>t0和任意常数ε>0,存在一个依赖于td和ε的常数v>0使得‖xr0(t)‖LS(C,CB) 则无人艇是关于集合LS(C,CB)集合跟踪. 为实现第二个控制目标(即n艘无人水面艇均匀分布在羽流边界上),无人艇之间必须交换信息.通常无人艇之间通信可用图来建模.考虑到通信复杂度和通信拓扑的易拓展度,本文选择最近邻线无向图.如图1所示,1号无人艇与2号艇通信,i(1 图1 由8艘无人水面艇构成的海洋机器人网络中边界领导艇、跟随艇分配及最近邻线图通信拓扑Fig.1 The assignment of boundary leader robot,boundary anchor robot,and follower ones,and nearest-neighbor-line graph communication topology in a mobile sensor network with 8 USVs 在图1中,红色方形、蓝色圆形、紫色三角形与绿色虚线分别表示边界领导艇、跟随艇、锚艇以及临近节点间通信链.在最近邻线型通信拓扑结构下,描述此无向图的拉普拉斯矩阵为 显然矩阵L是半正定的(即L≥0).此矩阵的半正定性质将用于后续的协同控制算法分析.Ni,i ∈N ≜{1,2,···,n}刻画与i号艇通信的所有艇编号构成的集合,其具体定义为 在研究工作[10,12]基础上,根据溢油羽流动态模型(1)–(3)和无人水面艇运动学模型(6),本节将在领导–跟随–锚策略下进一步提出基于分布一致观测器的协同控制算法. 首先利用n艘无人艇所配备的化学浓度传感器测量到各自位置处的局部羽流浓度信息 其中l(U(xri(t))),i ∈N为常数且均相同,即 和ωi(t),i ∈N是测量干扰并满足|ωi(t)|<ωmi,ωmi>0,i ∈N是给定的常数,构造具有如下形式的分布一致偏微分观测器 根据观测器方程(12),分别为边界锚艇、跟随艇、边界领导艇构造如下协同控制律. 其中k4>0是给定的控制参数和sgn(·)是符号函数. 为衡量协同控制律(13)–(15)的性能,引入以下3类误差指标. 此指标刻画协同控制算法的编队控制性能(即在羽流边界上无人水面艇编队的均匀性). 定理1从理论角度严格分析了所提出协同控制算法(13)–(15)的性能. 定理1在假设1下,考虑由二维空间对流–扩散方程(1)–(3)描述的溢油污染羽流扩散方程、受运动学方程(6)约束的n艘无人水面艇以及协同控制算法(13)–(15).对给定常数wm>0,ωmi>0,i ∈N,系数矩阵D≜diag{d1,d2}>0,控制增益ki>0,i ∈{1,2,3,4},观测器增益Li >0,i ∈N和一致观测器增益Lc>0,在过程干扰w(x,t)和测量干扰ωi(t)分别满足和|ωi(t)|<ωmi,i∈N前提下,有如下结论成立: a) 羽流场协同估计误差均值指数收敛于一个事先给定的以零点为圆心的邻域内,其半径依赖于wm和ωmi,i ∈N; b) 羽流场协同跟踪误差均值指数收敛于一个事先给定的以零点为圆心的邻域内,其半径依赖于wm和ωmi,i ∈N; c) 协同编队误差均值收敛于事先给定有界区域内. 证本证明主要由3部分构成:a)协同估计误差分析;b)羽流边界协同跟踪误差分析;c)协同编队误差分析. 在羽流边界协同跟踪误差分析部分,已经得到下列结论:尽管过程干扰w(x,t)和测量干扰ωi(t),i∈N存在,协同控制算法(13)–(15)依然能驱动n艘水面无人艇运动到羽流边界附近且随着羽流边界的扩张而动态扩张.众所周知,对于大多数羽流场,边界附近的浓度、梯度和散度均有界的且通常情况下值很小.因此,均有界,即存在一个常数τ >0使得 因为E(t)ET(t)≥0且L≥0,所以从不等式(46)和(47)可得到如下结论:随着t →∞,系统(44)的解收敛到一个以一致性值为中心的小区域,其区域半径由τ >0决定. 证毕. 注1根据定理1的证明可知,如果过程模型完全已知且浓度测量精确,即不考虑过程干扰w(x,t)和测量干扰ωi(t),i ∈N的影响,协同控制算法(13)–(15)可保证羽流场协同估计误差和羽流边界协同跟踪误差指数收敛. 注2在协同控制算法(13)–(15)中,本文通过控制增益k3n(t)切换实现第2个控制目标.结合文献[12]的工作,第二个控制目标还可通过通信拓扑切换实现.具体来说,当两艘边界领导艇在羽流边界上相遇(或两者之间距离小于某给定值),将最近邻线型图通信拓扑切换到最近邻环型图通信拓扑[12]. 设仿真区域Ω为[0,14]×[0,21]的矩形.在此区域内,两个化学源头(记为Y1和Y2)分别设定在位置[9 6]T和[7 8]T处,其中浓度值分别为2和3.令扩散系数矩阵为D=diag{0.5,0.5},羽流边界阈值为Cf=0.1 且外部干扰w(x,t)为w(x,t)=0.1 sin(πx)·exp(−0.01t). 类似于文献[12],仿真环境包括海面洋流场v(x,t)虚拟仿真和羽流浓度场C(x,t)虚拟仿真.海面洋流场v(x,t)是通过利用文献[15]提供的算法数值近似求解空间区域Ω内带有预设边界速度的不可压缩羽流场纳维–斯托克斯方程.在位置[9 6]T和[7 8]T处的两个泄漏源持续向流场中释放化学物质,这些化学物质在流场中传播形成了一个动态羽流浓度场C(x,t).此动态浓度场可通过数值求解的空间二维对流–扩散方程(1)–(3)近似获得. 针对由30艘水面无人艇构成的同构型海洋机器人网络(即n=30,N≜{1,2,···,30}),本节给出了所提出协同控制算法的数值仿真来验证其有效性.两个化学物质泄漏源在t=0时刻开始泄漏(t0=0).在化学物质泄漏1 s后,含有30艘无人艇的同构型海洋机器人网络被随机部署在区域Ω内(td=1 s),如图2所示,其中伪色彩表示每时刻羽流浓度分布其边上的色条显示比例,黑色曲线是羽流边界的轮廓,阈值浓度值为Cf=0.1,跟随艇被标记为蓝色圆圈‘○’,边界领导艇标记为红色方框‘□’,边界锚艇标记为紫色三角形‘Δ’,标记为Y1和Y2的两个位置分别是化学物质泄漏源,且无人艇的初值位置为 图2 针对由30艘水面无人艇构成的海洋机器人网络基于领导–跟随–锚结构海洋溢油羽流边界协同监测一次仿真运行中无人艇运动截图Fig.2 The snapshots of the vehicle movements for a simulation run with the marine robot network consisting of 30 USVs for boundary-leader-follower-anchorbased cooperative dynamic plume monitoring 其中rand(2,30)是一个2×30的矩阵,其元素取值于区间(0,1)内均匀分布的随机数.假设艇载浓度传感器所测量的羽流浓度值受到测量干扰为取值于区间(−0.03,0.03)内的随机噪声.过程噪声为w(x,t)=0.1 sin(πx)exp(−0.01t). 在协同控制算法(13)–(15)中,相关参数取值分别为Lc=30,Li=5,i ∈N,k1=70,k2=25,k3=4,k4=5.在边界领导艇控制律(15)中,当条件‖xr1(t)−xr30(t)‖≤2得到满足时,控制增益k3n(t)切换到(16).类似于文献[12],为降低初始估计误差对控制性能的影响,海洋机器人网络要充分收集任务区域内相关信息.为此,在本节仿真中,所有无人艇在初值位置固定不动以搜集任务区域内羽流浓度信息,直到4 s后才在协同控制算法(13)–(15)驱动下运动. 如图2所示,30艘无人艇在协同控制算法(13)–(15)引导下跟踪羽流边界(由黑色轮廓线刻画)的动态扩张,并在此羽流边界上保持均匀分布.具体来说,在t=8 s之前,边界领导艇引导跟随艇在羽流边界上散开(见t=6 s和t=7 s时刻截图)以有效监视羽流边界的动态扩张.在时刻t=8 s之后,边界领导艇控制算法(15)中控制增益k3n(t)已切换为(16)以实现边界领导艇与边界锚艇一起运动,且随羽流边界扩张而扩张(见t=10 s和t=18 s时刻截图).此外,为进一步说明协同控制算法的工程应用效果,图3中展示了由(17)–(19)定义的三类误差随时间的演化轨迹,以及30艘无人艇的运动轨迹,其中Y1和Y2是两个化学物质泄漏源,空心圆圈、方形框、三角形框及其实心形状分别表示无人艇初始和最终位置.这些仿真结果说明即使存在过程干扰和测量干扰,本文所提出的协同控制算法(13)–(15)依然能提供令人满意的控制效果. 图3 无人艇运动轨迹和编队误差、羽流边界跟踪误差和估计误差时间轨迹Fig.3 The USV trajectories,the time trajectories of formation error,plume front tracking error,and estimation error 为进一步说明其优越性,下面将本文所提出的领导–跟随–锚协同控制算法与文献[12]中的无领导者协同控制算法进行仿真对比.在此仿真对比实验中,两种算法的仿真环境设定以及控制参数选取均相同,即 与之前的仿真一样,所有无人艇在初始位置固定不动以搜集任务区域内羽流浓度信息,直到4 s后才在各自协同控制算法驱动下运动.图4给出了仿真结束时受上述两种协同控制算法驱动的30艘无人艇在羽流边界上的分布情况.图5提供了由领导–跟随–锚协同控制算法驱动无人艇的编队误差、羽流边界跟踪误差和估计误差时间轨迹(红色实线).仿真结果表明:本文提出的领导–跟随–锚协同控制算法有效实现了在第2.3节设定的两个控制目标,而文献[12]的无领导者协同控制算法未能实现第2个控制目标(即30艘无人艇在羽流边界上形成均匀分布). 图4 仿真结束时30艘无人艇在羽流边界上的分布情况Fig.4 The distribution on the plume front at the end of simulation 图5 30艘无人艇的编队误差、羽流边界跟踪误差和估计误差轨迹Fig.5 The time trajectories of formation error,plume front tracking error,and estimation error for 30 USVs 另外,文献[12]的仿真研究已经指出:相对于初始位置随机布放,无领导者协同控制算法能提供更好监测效果,如果其初始位置设定为包含溢油源的期望形状.为此,将无人艇的初始位置重新设定为 并重新运行无领导者协同控制算法仿真实验.图5给出相应无人艇的编队误差、羽流边界跟踪误差和估计误差时间轨迹(蓝色虚线). 由图4和图5中仿真结果可知,即使存在过程干扰和测量噪声,相对于文献[12]中的无领导者协同控制算法,本文所提出的领导–跟随–锚协同控制算法能提供更好的控制效果. 在领导–跟随–锚框架下,本文提出了基于分布一致观测器的协同控制策略,引导由n艘无人水面艇构成的海洋机器人网络完成海上溢油污染羽流的协同监测任务.在所提的协同控制算法中,分布一致观测器技术不仅能实现整个空间区域内动态浓度场的无偏估计,还克服了无人艇局部位置处梯度信息难以直接测量导致的控制设计困难.结合Lyapunov技术、集合稳定概念和多智能体一致性理论,严格分析了所提出协同控制算法的收敛性.数值仿真实验直观地展示了所提出协同控制算法的有效性及其仿真应用效果.
2.4 无人水面艇之间通信


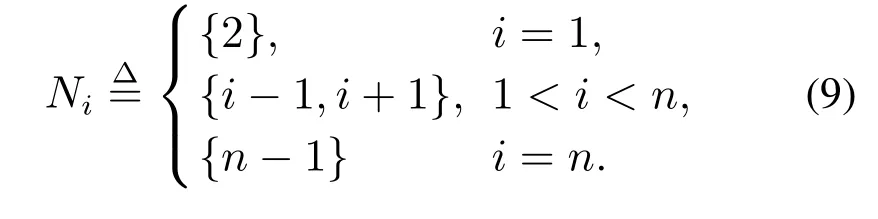
3 基于分布一致观测器的协同控制律设计











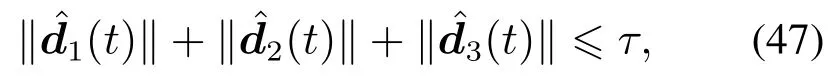
4 数值仿真
4.1 仿真环境
4.2 基于分布一致观测器的协同控制算法仿真




4.3 对比仿真实验





5 结论

