水下管道向下泄漏的羽/射流特性

张军，臧晓刚，张园春，何宏舟，陈怀民



水下管道向下泄漏的羽/射流特性

张军1，臧晓刚1，张园春2，何宏舟1，陈怀民1

（1集美大学机械与能源工程学院，福建省能源清洁利用与开发重点实验室，福建厦门 361021；2长庆油田勘探开发研究院，陕西西安710018）

对水下管道向下泄漏的羽流特性进行了实验及理论研究。采用拉格朗日控制体积分法建立了向下运动的羽动力模型，并对羽流参数进行了模拟。模拟结果表明模型对羽流半径及长度的预测与实验结果基本相符，但在接近羽流终端时，对羽流半径的预测结果要高于实验值。实验及模拟结果还表明，向下泄漏时羽流的初始动量衰减很快，与向上泄漏时羽流相比，羽流长度很短。随着Froude数的增大，向上羽流的长度增长较大，而向下羽流的长度却增长缓慢。

水下管道；向下泄漏；羽流动力特性；数值模拟；实验研究

引 言

随着海上油气田的不断开发及其他海上活动的日益增多，海底输油管道已逐渐成为石油天然气输送的有效工具[1-2]。这些海底管道虽然在经济建设中发挥着重要作用，但由于施工、人为事故、管道腐蚀等各种因素而对海洋环境破坏的潜在危害也日益增大[3-4]。因此，开展对水下油管泄漏及溢油运动规律的研究对于泄漏事故的风险评估、泄漏后的紧急响应及对污染物的控制有极为重要的实际意义。因水下泄漏产生的溢油最初是以水下射流或羽流形式释放的，因此，对水下羽射流动力学特性的研究对于理解溢油在水中的运动规律极为重要。有关这方面研究在不少文献中有所涉及[5-8]。如Hirst[5]对水下圆柱射流进行了研究，采用质量、动量、能量积分方程对射流的宽度、长度及射流轴线的温度分布进行了预测。Yapa等[6-7]针对海底溢油事故，采用拉格朗日积分法建立了溢油的浮羽动力学理论模型，模型考虑了周围海流状况及射流中油向周围海水中的扩散及溶解。Johansen[8]也建立了类似的Lagrangian型羽动力模型。其他学者对这些模型进行了进一步的改进，并对许多水下溢油事故进行了成功的预测[9-11]。文献[12]对浮羽射流的三维轨迹进行了实验研究，采用光衰减技术（light attenuation technique）对羽流的最高浓度位置进行跟踪。文献[13]考虑羽流因横向海流或水平动量的影响发生弯曲的因素，采用羽流的水平及垂直方向的质量、动量守恒及一个有关水的夹带率的经验公式，建立了一个水下油气水平释放的动力学模型。文献[14]采用拉格朗日控制体积分法及拉格朗日颗粒随机行走法较为全面地模拟了深水油气释放的迁移及归宿，模拟中考虑了水化物的生成。这些研究对于水下溢油事故的应急处理无疑提供了很好的理论指导，但这些研究均是针对水下溢油的向上（或者倾斜及水平）释放的，而目前对于水下溢油的向下释放却研究较少，而实际场合中很可能会遇到这种泄漏工况。如由于海底地形的变化，经常会出现悬跨管段，如果在管道下部因腐蚀或其他原因出现泄漏，将会产生油的向下泄漏释放，此时羽流在初始动量作用下首先向下运动，当初始动量耗费完后才开始在浮力作用下向上迁移，这将与油的向上泄漏时有极大的不同。文献[15]虽涉及水下悬跨管的向下泄漏，但仅采用商业软件FLUENT模拟了泄漏后油管周围的流场及温度场分布，没有涉及任何有关羽流动力学理论模型的建立，也没有进行相关的实验测试。基于上述原因，对水下管道向下泄漏及所形成的羽射流动力特性进行了一定的实验及理论研究，为这种工况下的水下溢油研究提供一定借鉴。

1 实验配置

实验是在静水箱中进行。实验配置如图1所示。油液由油泵1泵出，通过阀门2、压力表3，流入透明水箱8中的透明实验段5，实验段内径为30 mm，水平安装在水箱水中。在实验段中部下壁面开有直径为2 mm的泄漏孔，泄漏孔出口距离水箱底部为300 mm。在实验段泄漏孔的上下游分别安装精密流量计4、6（LWGY型涡轮流量传感器，量程0.02～2 m3·h-1，测量误差小于0.5%），用于测量泄漏流量。油液通过实验段后流回油箱。实验油品为柴油，密度为815 kg·m-3，动力黏度为0.00426 Pa·s。水箱中的水为自来水，密度为997 kg·m-3，动力黏度为0.001 Pa·s。实验中羽射流形态采用Sony ILCE-5100相机拍摄录像采集（拍摄速度为25 frame·s-1），通过安装在水箱上的标尺及图像放大倍率可获得羽流相关尺寸。通过调节阀2，可调节实验段内压力，从而获得不同的泄漏流量。

1—oil pump; 2—valve; 3—pressure gauge; 4,6—flowmeter; 5—transparent test section; 7—oil tank; 8—transparent water tank

2 理论模型

对于水下溢油的理论模拟，多数学者将溢油运动分为两个阶段来分别处理[6-7,11]。第1个阶段为羽动力阶段，即油液泄漏后形成的羽流，此时溢油主要依靠初始动量驱动。当初始动量消耗完后，大量油滴将主要依靠浮力及周围海流的作用而运动，此即第2个阶段——浮力阶段。在羽动力阶段，主要采用羽动力模型来获得油水混合物的运动规律，而在浮力阶段，一般采用拉格朗日颗粒跟踪法来模拟油滴群的运动，并最终获得溢油在水中的整个运动规律。由于本研究主要局限于水下管道向下泄漏的羽流特性，故这里仅限于羽动力模拟，而不涉及第2阶段溢油运动。对于向下泄漏的羽流，这里采用Yapa等[6-7]的拉格朗日控制体积分法来建立羽流动力模型。即在每一时刻将溢油及水混合物视为一系列控制单元体，通过控制单元体的质量、动量、浓度等守恒方程来建立羽流动力学模拟。假如不考虑油的压缩性、油在水中的溶解及水密度、温度等的变化，每个控制单元体守恒方程可建立如下：

质量守恒

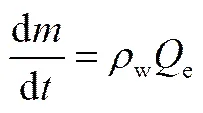
式中，为单元体内油水混合物质量；w为周围水的密度；e为周围水流的卷吸流率；为时间。

动量守恒

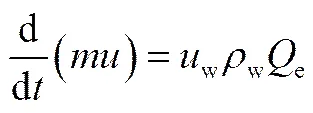
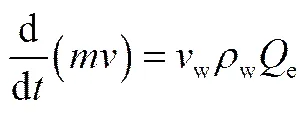
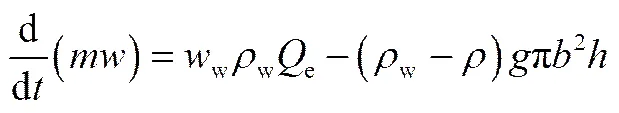
式中，、、分别为单元体混合物在、、方向的速度；w、w、w分别为周围水在3个坐标方向的速度；为单元体混合物密度；和分别为羽流的半径及厚度（=Δ）；式(4)右边第2项反映浮力对羽流的作用。假如速度为正，则浮力方向与之相反，这是与向上泄漏所不同的。

浓度守恒

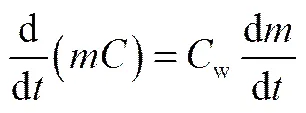
式中，为单元体内油质量浓度；w为周围水体中的油浓度。

对于卷吸流率，如仅考虑剪切卷吸，可表达为

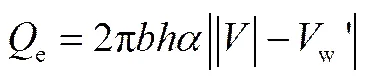
式中，为卷吸系数，许多学者进行了大量的实验研究，给出各种实验值[16]，这里采用文献[17]的实验关系式

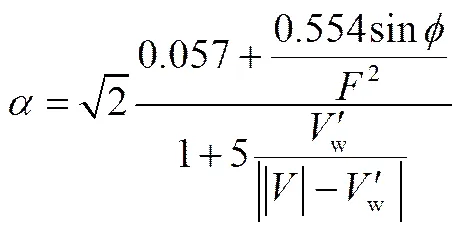
式中与羽流的Froude数有关，可表达为

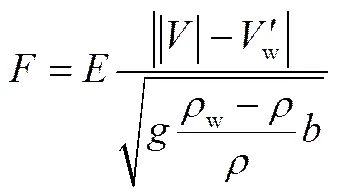
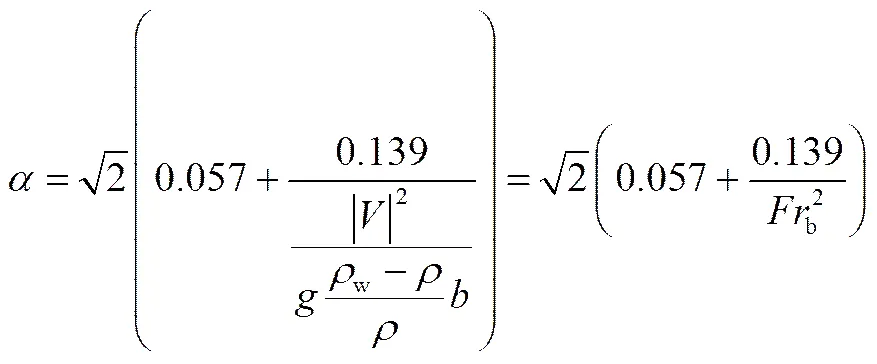
式(9)表明，卷吸量与羽流的局部Froude数b有关。

采用上述理论模型计算时必然涉及羽流的终止准则，即羽流最大延伸的长度。对于羽流终止准则，目前主要有3个准则[6-7,9]：①中性浮力准则（NBL，neutral buoyancy level），即在羽流上升过程中，羽流（油水混合物）密度达到周围水密度时，羽动力阶段将结束；②滴浮力速度准则（VC，droplet buoyant velocity criterion），即当羽流速度降低到油滴浮力速度时，羽流终止；③零速度准则（zero velocity criterion），即羽流速度变为0时，羽流终止。对于管道向下泄漏，羽流在初始动量作用下向下运动，当初始动量耗费完后，油滴群才开始在浮力作用下向上迁移。显然以零速度准则为羽流终止准则更为客观。为了揭示向下泄漏不同于向上泄漏羽流的一些特点，本研究也计算了向上羽流的运动规律[对于向上泄漏，浮力方向与羽流运动方向相同，故式(4)右边第二项的符号与向下泄漏时相反]。对于向上泄漏，研究表明滴浮力速度准则更加符合实际。而对于滴浮力速度准则，目前又有3种选取方法，分别为最大滴、最小滴及平均滴浮力速度。文献[9]曾对3种滴浮力速度准则进行过比较，认为选取平均滴浮力速度准则更为合适。故对于向上泄漏，计算时选取平均滴浮力速度准则作为向上羽流的终止准则。另文献[18]曾根据深水溢油释放实验数据进行分析，认为95%的油滴直径小于7.5 mm，油滴的平均滴径约为5 mm。为此，以5 mm油滴的浮力速度（约为0.085 m·s-1）为向上羽流的终止准则，即当羽流速度降低为0.085 m·s-1时，羽流达到最大长度。

以上公式可采用数值技术来计算，选取一定的时间步长，给定初始条件，便可计算出每个时间步的羽流半径、厚度、速度、质量、浓度等参数，从而描述羽流的动力学特性。本研究使用有限差分法来离散上述方程，并采用Matlab进行编程，对不同泄漏量下的向上及向下泄漏羽流的运动进行了模拟计算。计算时间步长Δ采用文献[17]所推荐的取值，即Δ=0.10/||，这里0为泄漏孔半径。计算初始值为：初始羽流半径为0，初始羽流速度为泄漏出口速度，初始羽流油浓度为1，初始羽流密度为油密度。

3 实验及理论模拟结果的分析及讨论

按照前面的实验配置，首先进行了泄漏实验研究。图2是实验中拍摄的不同泄漏量时的羽流的形态。由照片可见，油液的向下泄漏形成向下运动的羽流。在初始动量的作用下，羽流不断向下延伸。随着轴向距离的增大，周围的水不断被卷吸进来，羽流径向尺寸不断增大。当初始动量消耗完后，羽流轴向达到最大长度，不再向下运动，此时油滴群在浮力的作用下向上运动。随着泄漏量的增大，羽流的最大长度也逐渐增大，但与向上泄漏有所不同的是，羽流长度增大的幅度较为有限。

为了评价采用拉格朗日控制体积分法用于向下羽流运动的预测特性，图3给出了羽流半径的预测值与实验值的比较。该图实际上表征了理论模型对羽流形态的预测特性。比较可见，理论模型预测的射流半径变化趋势与实验结果基本一致。相对而言，泄漏量较小时，预测误差稍大。随着泄漏量的增大，预测值与实测值逐渐变得吻合。这主要是小泄漏量时流量的测量误差较大的缘故（本次工作泄漏量采用泄漏孔上、下游的流量计测量值之差而得）。随着泄漏量的增大，测量误差会减小，故大泄漏量时预测值与实测值更为相符。比较还表明，在轴向距离较大（接近羽流的终端）时，预测结果与实验结果的偏差有增大的趋势，这个原因可由羽流动力学模型的建立过程来解释。采用拉格朗日控制体积分法建立羽动力学模型时忽略了羽流断面上的速度分布，即假设羽流控制单元体上每个断面的速度均匀分布，而实际羽流截面上速度分布并不是均匀的，而近似呈指数分布，即轴线处速度最大，沿径向逐渐减小[12,19]。在接近羽流终端时，虽然羽流断面平均速度还没有降低为0，但羽流边缘处（径向最大位置）速度可能已为0，这会使得模拟的羽流半径在接近羽流终端位置时大于实际结果。此外，比较图3及图2照片还可发现，模拟的羽流长度与实验结果也是基本相符的（图2四种泄漏量下羽流长度大致分别为6～7、11～12、13～14、14～15 cm）。总体上来说，拉格朗日控制体积分法所建立的羽动力学模型基本能够反映向下泄漏时的羽流特性，尤其在较大泄漏量时，预测结果与实验结果有较好的相符性。

为了揭示向下泄漏时羽流不同于向上泄漏羽流的特点，图4给出了模拟的向上与向下羽流参数随轴向距离变化的比较（=6.95×10−6 m3·s-1）。从羽流运动过程来看，随着羽流的运动，周围水不断被卷吸进来，羽流半径不断增大，因此，羽流内油浓度逐渐减小、羽流混合物密度逐渐增大，初始动量不断被消耗，速度不断降低。图4清晰地演示了羽流的这一变化过程。与向上运动的羽流有所不同，向下运动的羽流参数随轴向距离的增大而变化得更快些。显著地体现在羽流半径增长很快，速度衰减很快，在接近0.1 m处速度就几乎衰减为0，羽流半径及长度达到最大，此时羽流浓度达到最小，密度达到最大，接近周围水的密度。可见，对于向下运动的羽流，羽流的最大长度极为有限，所有参数在很短的时间及距离内就达到终端。

对于羽流运动的模拟，卷吸系数是较为重要的参数，采用不同的值计算，模拟结果会有所出入。本文模拟采用文献[17]的关系式[即式(9)]来计算，它充分考虑了局部Froude数的影响。也有一些学者采用确定的卷吸系数[16]（如很多采用=0.086）。图5为卷吸系数对模拟的羽流半径的影响。由图可见，当采用式(9)来确定卷吸系数时，对羽流半径的模拟与实验结果更为相符，而卷吸系数取值为0.086时，预测结果稍微偏高。

在变密度浮力射流中，密度Froude数是一个重要的量纲1数，它可表征惯性力和浮力对羽流的影响程度，定义如下[20]

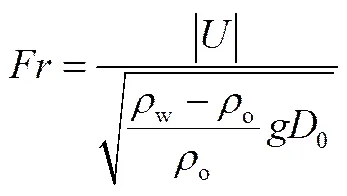
式中，o为油密度；为射流出口速度；0为泄漏孔直径。

为了表征浮力和初始动量对羽流的影响，图6给出了模拟的羽流最大长度与Froude数的关系。由图6可见，无论向上羽流还是向下羽流，其最大长度均随Froude数的增大而增大，这是必然的，因为Froude数越大，即意味着羽流所获得的初始动量越大，羽流在初始动量作用下所达到的长度也必然越大。但是，向上羽流的长度远大于向下羽流长度，并且随着Froude数的增大，向上羽流长度增长很大，而向下羽流却增长有限。从羽流动力学来说，羽流的运动主要依靠初始动量和浮力所驱动。对于向上运动羽流，初始动量与浮力方向相同，羽流在两者的共同作用下向上运动，随着羽流的运动，周围水被不断卷吸进来，羽流半径不断变大，截面速度不断变小，直到初始动量消耗殆尽，这个过程会花费较长的时间，因此羽流会延伸很长距离。而对于向下运动羽流，浮力方向与初始动量方向相反，除了卷吸作用会消耗初始动量外，羽流所受浮力也会极大地消耗羽流运动的动力，这使得向下羽流所形成的长度极为有限，即使在较大的Froude数下，向下羽流的长度也增长不大。向下羽流的这个特点对于水下管道泄漏溢油的模拟可提供这样一些有益的建议：在较小的Froude数情况下，相同泄漏量的向上及向下泄漏对于模拟溢油轨迹及溢油到达水面时间及位置差别不大，可忽略羽流长度（尤其对于深水管道泄漏），可直接用拉格朗日颗粒跟踪法来模拟油滴群的运动轨迹。但当Froude数较大时，虽然向下泄漏羽流长度增长有限，但忽略羽流长度可能会带来一定误差，因为在横向海流作用下，假如不考虑羽流长度，会使溢油轨迹预测发生一定的偏差，从而影响到溢油到达水面时间及位置的预测精度。因此，建议在较大的Froude数情况下，对于向下泄漏，仍应按照Yapa及其他学者所采用的方法[6-7]，将溢油分为两个区域来处理。即在羽动力阶段，按照拉格朗日控制体积分法来求解羽动力模型，当羽流初始动量消耗完后，再按照拉格朗日颗粒跟踪法来求解油滴群的运动轨迹，这样可保证较好预测精度。

4 结 论

对水下管道向下泄漏的羽流特性进行了实验及理论研究，可得以下基本结论。

（1）拉格朗日控制体积分法可用于向下运动羽流的运动描述，其对羽流形状及长度的预测与实验值总体相符。但由于拉格朗日控制体积分法没有考虑羽流截面的速度分布，故在接近羽流的终端时，预测的羽流半径要大于实验结果。

（2）模拟及实验结果表明，向下泄漏时羽流的初始动量衰减很快，与向上泄漏时羽流相比，羽流长度很短。随着Froude数的增大，向上羽流的最大长度增长较大，而向下羽流的最大长度却增长缓慢。

（3）对于深水管道泄漏，在Froude数较小时，向下泄漏的羽流长度可以忽略。在Froude数较大时，如忽略羽流长度，对于溢油运动模拟可能带来较大误差。

[1] WANG Z H, LI H B, PAN R S. Oil-gas multiphase transportation technology in a subsea pipeline: a case study [J]. Explorationproduction, 2012, 10(1): 34-37.

[2] 付长静, 李国英, 赵天龙, 海底管道与海床相互作用研究综述[J]. 水利水运工程学报, 2014, (6): 100-106. FU C J, LI G Y, ZHAO T L. On interaction between submarine pipelines and seabed under action of waves [J]. Hydro-Science and Engineering, 2014, (6): 100-106.

[3] ALAMILLA J L, SOSA E, SÁNCHEZ-MAGAÑA C A,. Failure analysis and mechanical performance of an oil pipeline [J]. Materials & Design, 2013, 50: 766-773.

[4] ILMAN M N. Analysis of internal corrosion in subsea oil pipeline [J]. Case Studies in Engineering Failure Analysis, 2014, 2(1): 1-8.

[5] HIRST E. Zone of flow establishment for round buoyant jets [J]. Water Resources Research, 1972, 8(5): 1234-1246.

[6] YAPA P D, LI Z. Simulation of oil spills from underwater accidents (Ⅰ): Model development [J]. Journal of Hydraulic Research, 1997, 35(5): 673-688.

[7] ZHENG L, YAPA P D. Simulation of oil spills from underwater accidents (Ⅱ): Model verification [J]. Journal of Hydraulic Research, 1998, 36(1): 117-134.

[8] JOHANSEN Ø. DeepBlow — a Lagrangian plume model for deep water blowouts [J]. Spill ScienceTechnology Bulletin, 2000, 6(2): 103-111.

[9] DASANAYAKA L K, YAPA P D. Role of plume dynamics phase in a deepwater oil and gas release model [J]. Journal of Hydro-Environment Research, 2009, 2(4): 243-253.

[10] NORTH E W, ERIC ADAMS E, SCHLAG Z,. Simulating oil droplet dispersal from the deepwater horizon spill with a Lagrangian approach [J]. Geophysical Monograph, 2011, 195: 217-226.

[11] YAPA P D, WIMALARATNE M R, DISSANAYAKE A,. How does oil and gas behave when released in deepwater? [J]. Journal of Hydro-Environment Research, 2012, 6(4): 275-285.

[12] KIKKERT G A, DAVIDSON M J, NOKES R I. Buoyant jets with three-dimensional trajectories [J]. Journal of Hydraulic Research, 2010, 48(3): 292-301.

[13] HISSONG D W, POMEROY J, NORRIS H L. A mechanistic model for hydrocarbon plumes rising through water [J]. Journal of Loss Prevention in the Process Industries, 2014, 30: 236-243.

[14] CHEN H, AN W, YOU Y,. Numerical study of underwater fate of oil spilled from deepwater blowout [J]. Ocean Engineering, 2015, 110: 227-243.

[15] 袁朝庆, 郝佳宁, 马良. 海底悬跨石油管道泄漏流场和温度场耦合分析[J]. 压力容器, 2013, 30(5): 23-27. YUAN Z Q, HAO J N, MA L. Coupling analysis of flow field and temperature field on spanning submarine oil pipeline after leakage [J]. Pressure Vessel Technology, 2013, 30(5): 23-27.

[16] LIST E J, IMBERGER J. Turbulent entrainment in buoyant jets and plumes [J]. Journal of the Hydraulics Division, 1973, 99(9): 1461-1474.

[17] LEE J H W, CHEUNG V. Generalized Lagrangian model for buoyant jets in current [J]. Journal of Environmental Engineering, 1990, 116(6): 1085-1106.

[18] JOHANSEN Ø. Development and verification of deep-water blowout models [J]. Marine Pollution Bulletin, 2003, 47(9/10/11/12): 360-368.

[19] GEORGE W K, ALPERT R L, TAMANINI F. Turbulence measurements in an axisymmetric buoyant plume [J]. International Journal of Heat and Mass Transfer, 1977, 20(11): 1145-1154.

[20] 汪守东, 沈永明. 海底管线溢油数学模型研究[J]. 大连理工大学学报, 2006, 46(Suppl.): 191-197. WANG S D, SHEN Y M. Study of mathematical model for oil spills from seabed pipeline [J]. Journal of Dalian University of Technology, 2006, 46(Suppl.): 191-197.

Dynamic characteristics of plume/jet from underwater pipe downward leakage

ZHANG Jun1, ZANG Xiaogang1, ZHANG Yuanchun2, HE Hongzhou1, CHEN Huaimin1

(1Fujian Province Key Laboratory of Energy Cleaning Utilization and Development, Jimei University, Xiamen 361021, Fujian, China;2Research Institute of Changqing Oil Exploration & Development, Xi’an 710018, Shaanxi, China)

The plume dynamic characteristics from underwater pipe downward leakage are experimentally and theoretically investigated. The Lagrangian integral method is used to establish the dynamic model of downward plume. The model is numerically solved and the main plume parameters are obtained. The simulated results show that the simulated values in plume radius and length are generally consistent with the experimental values, but the simulated radius is higher than experiment value in area near plume terminal. The experimental and simulated results also show that for downward leakage the initial momentum of plume quickly decays and the plume length is very short compared with upward leakage. With increasing Froude number, the maximum length of upward plume rapidly grows while the maximum length of downward plume slowly grows.

underwater pipe; downward leakage; plume dynamic characteristics; numerical simulation; experimental investigation

date: 2016-01-08.

ZHANG Jun, bull0202@sina.com

10.11949/j.issn.0438-1157.20160034

TQ 021.1；X 55

A

0438—1157（2016）12—4969—07

福建省自然科学基金项目（2014J01201）；福建省科技计划项目（2014H6019）。

supported by the Natural Science Foundation of Fujian Province (2014J01201) and the Fujian Provincial Science and Technology Project (2014H6019).

2016-01-08收到初稿，2016-09-19收到修改稿。

联系人及第一作者：张军（1966—），男，博士，副教授。