不同充气条件下密相输运床返料系统气固流动数值模拟
马乔,雷福林,张亚文,阳绍军,徐祥,肖云汉
不同充气条件下密相输运床返料系统气固流动数值模拟
马乔1,2,3,雷福林2,3,张亚文1,2,3,阳绍军2,3,徐祥2,3,肖云汉2,3
(1中国科学院大学,北京 100049;2中国科学院工程热物理研究所,先进能源动力重点实验室,北京 100190;3中国科学院能源动力研究中心,江苏连云港 222069)
采用计算颗粒流体力学对密相输运床返料系统内的气固流动行为进行了数值模拟,分析了曳力模型和颗粒最大堆积浓度等参数对模拟结果的影响,确定了合适的模型参数。通过对比3组工况的模拟结果,获得了与实验结果基本一致的立管压力分布和固体循环流率随充气条件的变化规律,并分析了立管内压力梯度分布、气体流动方向、颗粒浓度分布等。结果表明立管充气口处压力梯度绝对值为局部最大值;当立管充气口气量为零时,会使充气口上方一段距离的压力梯度绝对值较小;充气量增大到一定值时会在充气口附近形成明显的气泡。当缺少立管高位充气时,会导致立管下部区域形成大的压力梯度,增加颗粒下落阻力。充气松动颗粒的作用仅对充气口附近区域有一定影响,更大的作用是在立管内形成均匀的压力梯度分布,使立管内气固流动状态保持上下一致。在制定充气方案时,应根据固体循环流率确定立管压降,补充合适气体量以维持气体下行速度均衡,使得各段的平均压力梯度相同。
返料系统;移动床;数值模拟;气固两相流
引 言
密相输运床是一种高通量高密度循环流化床,以高固体循环流率和密相悬浮上升流为其主要特征,具有高效的气固混合、传热、化学反应等优点,在煤气化方面具有很大的应用潜力。密相输运床循环回路主要由提升管、旋风分离器、立管和返料控制阀等构成。其中返料控制阀采用非机械阀,用于将立管底部颗粒回送到提升管底部。立管中则存储着高料位的物料,防止气体通过立管反蹿到旋风分离器而破坏系统平衡。颗粒在立管和返料阀中的流动特征能很大程度上影响整个系统的性能。密相输运床的物料循环过程主要通过不同的充气条件组合控制,使操作具有灵活性,适用于变工况运行,但充气不当容易产生系统不稳定。
由于返料系统在气固循环系统中的重要性,研究人员对其进行了大量实验和理论研究。Ludlow等[1]基于实验结果提出了估算料位高度和空隙率分布的立管模型。Basu等[2]和Kim等[3]对返料阀内颗粒运动基本原理进行了研究,从理论上分析了运行参数对颗粒循环流率、立管内物料高度和压力梯度的影响。Leung等[4]分析了负压差移动床里的流动结构。由于负压立管内流动形式的复杂性,张济宇等[5]和李洪钟[6]分别对立管稳定性控制进行了相关研究。这些研究获得的实验数据都是基于特定的实验平台,得到的结论或经验关系式还不具有普适性。在工业装置方面,由于测量难度较大和测试条件苛刻,得到实验数据有限,难以全面分析系统流动特性。
由于密相输运床装置较高,颗粒存料量较大,循环回路中不同区域气固流型差异巨大,其中返料系统内颗粒处于非流化下行移动床流型而提升管内为密相悬浮上升流,因此建立统一的模型方法具有很大的挑战性。同时由于立管内颗粒处于堆积状态,通常的实验方法无法测量颗粒的浓度和速度分布,为分析立管内流动增加了障碍。计算机技术的发展使得计算流体力学在气固流动模拟方面得到广泛应用,各种气固模拟方法被提出并得到快速发展。相比于实验,采用数值模拟的方法能获得更为全面的数据,如在分析立管流动时,可以很容易地得到固相浓度分布、气固相速度分布以及压力梯度分布等,这些数据对于理解气固流动行为以及装置的设计与运行都很有帮助。
目前,适合于宽浓度范围颗粒流的模拟方法主要有双流体模型和离散元模型。双流体模型可以模拟较大规模的装置,但不能有效用于非完全流化的立管返料模拟[7-8]。离散元模型能准确模拟颗粒间作用力,适用于返料系统中各种复杂流型,但是计算非常耗资源,能模拟的颗粒数还较少,无法做大尺度的气固流动模拟,限制了其在工业领域的应用[9]。近年来,兼顾了双流体模型和离散元模型优点的计算颗粒流体力学(CPFD)方法得到越来越多的应用。CPFD是基于多相质点网格(MP-PIC,multiphase particle-in-cell)模型,其单个计算颗粒由很多性质相同的实际颗粒组成,从而能实现工业规模级别的颗粒系统模拟,并且还可以考虑颗粒粒径分布。CPFD作为一种离散颗粒方法[10],直接计算颗粒的受力情况,因此能模拟非流化的颗粒运动,适用于立管内下行移动床流型的模拟[11-14]。
本研究选用CPFD模拟方法,对密相输运床返料系统的气固流动行为进行数值模拟,通过与实验结果对比验证该方法模拟立管颗粒流的可行性。此外,通过参数敏感性分析研究模型重要参数的影响。最后对3组不同工况进行模拟,研究了立管充气条件对返料系统气固流动特性的影响。
1 实验描述
密相输运床冷态实验装置如图1所示,主要包括提升管、一级旋风分离器、二级旋风分离器、立管和J阀等。空气通过布风板进入提升管,携带着从J阀返入的固体颗粒沿提升管上升,到达提升管顶部后,经出口结构改变运动方向进入一级旋风分离器。大部分颗粒被一级旋风分离器捕集而下落进入一级立管,而大部分气体与颗粒分离后通过旋风顶部出口进入二级旋风分离器,其将颗粒进一步捕集下来,通过二级立管和U阀返回一级立管。颗粒沿一级立管向下移动,到达立管底部后通过J阀送回提升管,实现固体颗粒的循环。
实验装置的提升管高度(布风板以上部分)约为18.3 m,提升管和立管中心轴线间距为1.5 m;提升管和J阀内径均为0.1 m,立管内径为0.13 m。J阀斜管与水平面角度为30°,这是通过试验不同角度的J阀确定的,它能实现较大的固体循环流率、较好的调节性能和运行稳定性。各充气口位置及编号如图1(b)所示,在J阀上布置有X1、X2两路充气,立管上布置有间距为2 m的L1~L4四路充气,各充气管内径均为0.03 m,立管底部布置有布风板形式的充气口A。沿立管以1 m间距均匀布置多个压力传感器来测量压力分布。实验中采用堆料法测量固体循环流率。
实验采用B类石英砂颗粒作为物料,其真实密度为2996 kg·m-3,堆积密度1740 kg·m-3,自然堆积浓度为0.58,平均粒径为106 μm,颗粒粒径分布如图2所示。其中,真实密度测量采用浸水法,用颗粒质量除以浸水测得的体积计算;堆积密度测量采用堆料振实的方法,用颗粒质量除以其对应的具有轻度振实的堆积颗粒体积计算;颗粒粒径分布测量采用不同目的筛网筛分颗粒获得。
选取了3组实验工况,其相关充气操作条件见表1,其中J阀充气量上保持一致,仅改变了立管充气量,以分析立管充气对返料的影响。3组实验工况的测量结果见表2,其中固体循环流率基于提升管截面积计算。

表1 实验工况的充气量(标况)
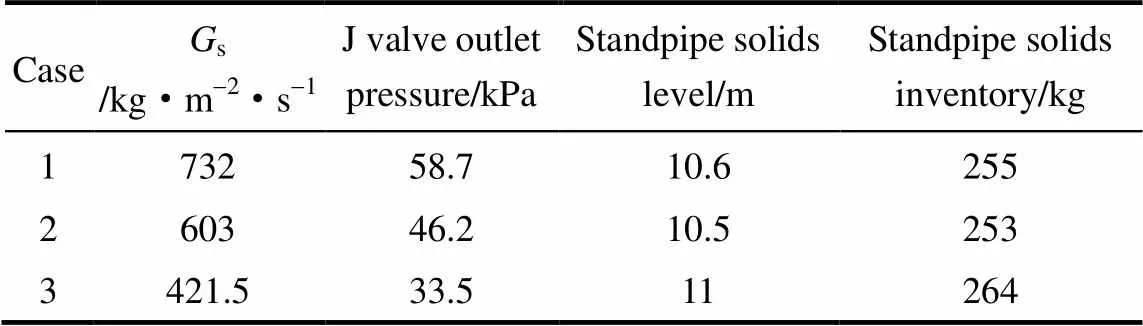
表2 实验测量结果
2 数值模拟方法
2.1 数学模型
计算颗粒流体力学是一种欧拉-拉格朗日方法,其将气体作为欧拉连续相,将固体颗粒作为拉格朗日离散相,主要控制方程如下[15-16]:
气相连续性方程

气相动量方程

式中,g为气相体积分数;g为气体密度;为压力;g为气体应力张量;为重力加速度;为气固相互作用力。
颗粒相采用MP-PIC方法处理。颗粒运动通过求解颗粒分布函数(,p,p,p,) 的Liouville方程

式中,p为颗粒加速度。本研究采用考虑接触应力加速度的混合加速模型[17]

式中,为曳力系数;D为颗粒碰撞松弛时间[18];c为接触应力加速度[17]
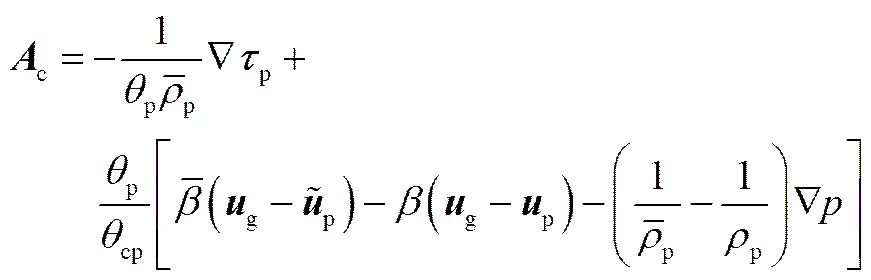
式中,cp为颗粒堆积极限体积分数;p为颗粒应力[16]

式中,s为压力常数;为10-7量级的小数;为2~5的常数。
气固相互作用力为单颗粒曳力的积分

式中,p为颗粒体积。
气固曳力模型对计算结果的影响很大。考虑到立管气固流动横跨稀相流到移动床,本研究采用Wen-Yu/Ergun组合模型,并分析不同曳力模型的影响。Wen-Yu模型表达式如下[19]
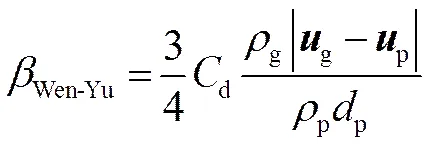
式中,p为颗粒直径,


Ergun模型表达式为[20]
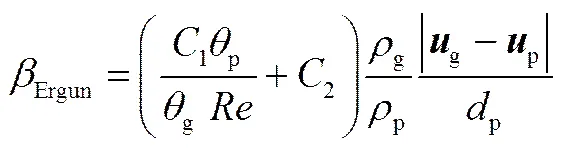
式中,1、2为常数。
Wen-Yu/Ergun组合模型表达式为
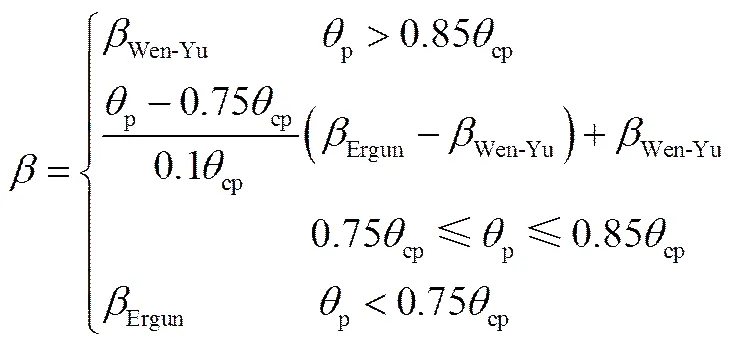
原始的Ergun模型中1、2系数分别为150和1.75(Ergun 1模型);在CPFD方法中,这两个系数修改为180和2(Ergun 2模型)。根据1、2的不同取值,选取了Ergun 1模型、Ergun 2模型、Wen-Yu/Ergun 1组合模型和Wen-Yu/Ergun 2组合模型等曳力模型用于模拟对比。表3为本研究模拟中用到的曳力模型。

表3 曳力模型
2.2 模拟设置
在气固循环回路中存在完全不同的流型,气固间作用也存在明显差异。本研究主要关注立管内颗粒流动,同时为了减少计算量,采用图3所示的返料系统几何模型,其主要包括一级旋风分离器、立管和J阀。
返料系统中初始物料量根据实验中观测的稳定料位高度确定(表2),颗粒初始分布区域为J阀和立管内料位高度以下区域,颗粒初始化浓度为0.58。各充气口和旋风入口为速度入口边界条件,具体数值根据表1中所列的空气流量设置,其中,在旋风入口给定提升管气量r。对气相,J阀出口和旋风分离器顶部设置为压力边界条件,J阀出口压力值根据表2所示实验值设定。考虑到二级旋风和除尘设备的压降,所有工况的旋风分离器顶部压力都设为5 kPa。对固相,J阀和旋风分离器出口设为出流边界,并实时监测出口流出的颗粒流率;为了保持系统内物料平衡,将J阀流出的物料返回到一级旋风分离器入口,而从一级旋风出口流出的物料则通过2 m3·h-1的气体(标况)流量从二级返料口输送回一级立管,如图3所示。
气相采用无滑移边界条件,气相湍流用LES模型计算;固相考虑与壁面的能量损耗,颗粒-壁面法向/切向恢复系数参考CPFD方法的推荐值以及文献中的常用值[11],分别设为0.3和0.95。除非特殊说明,颗粒最大堆积浓度cp设为0.58,曳力模型为Wen-Yu/Ergun 2模型。时间步长设置为变时间步长以加速计算,最大时间步长限制为5×10-4s。每个计算工况模拟时间80 s,以确保计算达到稳定,并选取60~80 s的时均值作为稳态计算结果。
相关研究表明[21-22],曳力模型和颗粒最大堆积浓度对模拟结果会有较大的影响,因而进行相关的参数敏感性分析以选取合适的模型参数。
2.3 网格无关性分析
选取网格尺寸时需要在计算精度和计算效率间取得平衡,因此有必要进行网格无关性分析。由于离散颗粒和流体网格的描述尺度不同,颗粒信息需要映射到网格上,因此需要一定尺寸的网格来容纳足够数量的计算颗粒以保证统计权重,同时尽量采用较少的颗粒数减少计算量。计算网格采用沿坐标轴线的笛卡儿网格,边界则采用与几何边界一致的切割体网格。依据文献[23]对一台循环流化床装置模拟采用的网格尺寸为参考,结合所研究装置的尺寸,选取了3组不同尺寸的网格进行比较分析,见表4。对于表4中的3种网格,保持每个网格中的计算颗粒数不变,总计算颗粒数与网格数呈正比关系。

表4 3种计算网格信息
模拟工况选取表1所示的实验工况1,图4为采用3种网格计算获得的立管轴向压力分布结果。从图中可以看出,网格1和网格2计算的轴向压力分布基本相同,仅在立管底部和料位面附近存在较小差异,而网格3计算的轴向压力分布则存在明显区别,特别是3 m到料位面(11 m)之间的压力分布已经完全偏离实验值。
图5为采用不同网格尺寸模拟得到的固体循环流率。从图中可以看出,随着网格尺寸的减小,网格1和2模拟的固体循环流率结果趋于一致,而粗网格3模拟的固体循环流率相差较大。平衡计算精度和计算效率,选用网格2(即13 mm×13 mm×26 mm网格)作为以下所有模拟计算的网格。
3 结果与讨论
3.1 曳力模型的影响
曳力作为驱动颗粒运动的动力来源能极大地影响模拟结果。对于立管内已接近堆积状态的颗粒流动,选取了表3所示的4种曳力模型用于模拟对比。图6为采用不同曳力模型获得的沿立管轴向的压力分布。从图中可以看出,由于Ergun 2模型相比于Ergun 1模型采用更大的系数,计算的曳力更大,最终Ergun 2模型计算的沿立管压力分布与实验结果产生较大偏差,而Ergun 1模型得到了与实验比较接近的压力分布。Wen-Yu/Ergun 1组合模型和Wen-Yu/Ergun 2组合模型模拟得到的立管压力分布与实验结果都比较接近,但是Wen-Yu/Ergun 2组合模型在6 m以下区域与实验结果更为接近。表5为不同曳力模型计算的固体循环流率,可以看出Ergun 1模型和Wen-Yu/Ergun 2组合模型的循环流率模拟结果与实验结果比较接近。综合对比压力和循环流率模拟结果,并考虑更宽的颗粒浓度适用范围,最终选取Wen-Yu/Ergun 2组合模型作为以下模拟分析的曳力模型。

表5 不同曳力模型计算的固体循环流率
3.2 颗粒最大堆积浓度的影响
颗粒最大堆积浓度cp取决于颗粒的尺寸、形状、空间排列等,即使处于堆积状态的流动颗粒也还有可能发生颗粒间位移或重新排列而使颗粒体积分数达到或超过静止时的堆积浓度[13]。
CPFD方法采用颗粒应力模型来描述颗粒间接触作用力,颗粒应力在颗粒接近堆积状态变得极为重要。在密相输运床系统中,立管和J阀存在明显的颗粒堆积区域。在这些区域,最大堆积浓度会很大程度上影响立管和J阀中的气固流动模拟结果。本研究选取了0.56~0.6之间的4组不同的最大堆积浓度进行模拟,通过对比实验结果来选取最优的颗粒最大堆积浓度。
图7为采用不同最大堆积浓度时模拟得到的立管轴向压力分布结果。从图中可以看,除了cp=0.57外,其他3组模拟的压力分布与实验值基本一致,其中cp=0.6时与实验结果吻合较好。同时也可以看到随着cp增加,立管中下部的压力分布也逐渐增加。随着cp增加,静止床高减小,造成立管上部的物料量减少而更容易流化,因此上部的压力随cp的变化趋势与中下部不同。由于立管底部与J阀连接,是气固流动的转向区域,通过对比发现模拟的底部压力变化趋势与实验值一致,但要低于实验值。
图8为采用不同最大堆积浓度时模拟得到的固体循环流率。从图中可以看出,固体循环流率随着cp的增加而增加,但cp=0.6时的循环流率相比于cp=0.59时基本没变化。当cp=0.58时,模拟结果与实验结果最为接近。综合考虑压力分布和循环流率的计算结果,选取0.58作为以下模拟计算的参数。选取的cp与实验测量的物料自然堆积浓度一致,说明在选取此参数时,自然堆积浓度可以作为很好的参考值。
3.3 不同充气条件下立管流动特性
为了分析充气条件对立管气固流动特性的影响,对工况1~3进行了数值模拟。工况1~3的充气操作条件见表1;边界条件和立管内初始物料量参考表2。
图9为工况1~3的固体循环流率模拟结果和实验结果对比,从图中可以看出,模拟结果能比较准确地预测出不同充气条件下的循环流率变化趋势。但在低循环流率下模拟结果误差较大,可能是由于充气量较小时,立管内几乎所有区域的颗粒浓度都接近最大堆积浓度,混合加速度模型中的接触应力加速度过大,导致模拟结果大于实验值。
图10为工况1~3立管内轴向压力分布模拟值与实验值对比。从图中可以看出,随着立管充气量减少,立管总压降相应地减小。图中3个工况的模拟结果与实验结果在整体分布上有较好的一致性,但在底部区域与实验值有所偏离。这是由于在立管底部0~2 m区域发生流动转向,存在流型转变,这一过程中颗粒受力较难准确计算,导致模拟结果与实验结果存在差异。
图11为不同工况下的压力梯度分布,可以看出压力梯度变化较大的区域分布在充气口附近区域。这是因为充气口为局部压力极大值点,充入的气体向上、下两方向扩散,使得充气点上方附近气固滑移速度加大,压力梯度增大,而充气点下方附近气固滑移速度减小,压力梯度减小。充气口形成的空腔会对流动产生扰动,工况2和3的L4充气口即使没有充气也引起了压力梯度的微小变化,但对总体变化趋势没有产生明显影响。
工况1条件下立管中段压力梯度分布比较均匀,各充气段的压力变化比较一致,而工况2和3的压力梯度在两个充气口之间线性变化,形成“锯齿”形压力梯度分布。工况2和3由于充气口L4没有充气,在L4上方一段距离内压力梯度接近于零,使压力累积到下部区域,在L4和L3充气口间形成急剧的压力梯度变化。因此,当立管没有高位充气时,立管底部充气会使立管下部形成高压力梯度分布,这种压力梯度分布很容易在立管中部形成气相逆流区,破坏颗粒稳定下落。
图12为工况1~3立管中心剖面上各充气口附近的瞬时(80 s)气相速度矢量图和时均颗粒浓度等值线图,从左往右依次为L1~L4充气口。由于图中各区域的速度大小差异较大,因而没有用矢量长度来表示速度大小,速度矢量仅表示流体相的局部流动方向。由颗粒浓度的等值线可以判断出气泡大小,从图12中可以看出,由于工况1的充气量较大,相同充气口附近的气泡也相对较大。对比同一工况不同充气口位置气泡大小,可以看到由于下部压力大于上部压力,相同充气量条件下位于立管下部的充气口气泡大小要小于上部充气口气泡。位于上部的气泡不仅在径向方向深入更多,在轴向方向也同样有更大延伸。特别是L3充气口距离料位面较近,压力相对较低,因此相同充气量下流速较高,产生的气泡最大,并容易在大的充气量下产生占据整个截面的气栓。工况3由于充气量较小,因此产生的气泡也较小。从气相速度矢量图中可以看出L1和L2的充气对气体流动方向有一定影响,气体在气泡内产生回流。L3充气口对气相流动有较大影响,在此充气口会有一部分气体沿立管边壁向上流动。如果充气量过大,立管上部存在气相整体向上流动的区域。从整个立管的流动来看,气体被下落的颗粒携带流动,最终具有与颗粒相近的速度,在立管内形成气固一致向下的流动。
图13为3个工况下充气口附近的时均颗粒浓度分布云图。从图中可以看出颗粒浓度不是关于充气口对称分布的,同时也可以看到充气量需要达到一定量才会在充气口附近形成明显的气泡。立管内绝大部分的颗粒都处于堆积状态,仅在充气口附近存在一定的固相低浓度区。充入气体的作用不只是松动颗粒,减少颗粒间接触摩擦,更重要的是补充气量以维持在更高压力下的气体流速相对稳定,在立管内形成整体相对均匀的压力梯度分布,避免在底部形成大的压力梯度而阻碍颗粒下行,恶化返料过程。
对比各工况的充气条件,工况1和2的L1充气量(标况)分别为0.8、0.6 m3·h-1,但由于底部气体压力较高,使得充入气体的气速较低,充气对充气口附近的颗粒浓度影响较小,两个工况在L1附近的气固流动行为较为相似。工况1和2的L2、L3充气量(标况)分别为0.8、0.6 m3·h-1,但工况2的充气形成了变化更为急剧的压力梯度。一是因为工况1的循环流率较大,更多的气体随颗粒向下流动,使气固滑移速度分布较为均匀。二是因为工况2的L4缺少充气,无法使上部颗粒流化,造成下部压力积累,在两个充气口间形成较大的压力变化。工况3的充气量与前两个工况相比要小,并从L1到L3逐渐递减,使得下部的负压力梯度的绝对值较大,产生较大的气固曳力减缓了颗粒的整体流动速度,使工况3的固体循环流率更小。
综上所述,合理的充气能使立管内压力梯度分布较为均匀,提高返料系统的固体循环流率。对于本研究的实验装置,立管的料位高度约为10 m,运行过程中立管底部和顶部的压力差很大,但是稳定运行时立管下行移动床的空隙率沿高度变化不大,固体颗粒下行速度基本恒定。如果立管不充气,因为气体可压缩导致立管下部的气体下行速度减小,气固滑移速度增加,使得气固曳力增大而阻碍颗粒下行;另一方面,如果立管不充气,立管下部固体颗粒间的接触应力增大,导致摩擦力增大而阻碍颗粒下行。充气的作用是尽量均衡立管上下部的气固滑移速度和颗粒间的接触应力,使立管内气固流动状态保持上下一致。立管内单位料位高度所需充气量的大小是与立管压力梯度、固体循环流率密切正相关的,而立管压降需要平衡J阀、提升管、旋风分离器等的压降,也与固体循环流率正相关。归根结底,立管充气量与固体循环流率密切正相关,它们之间具有一定的匹配关系。实际上,因为充气口数量有限,充气沿高度分布是不连续的,可能在充气口附近产生急剧变化的压力梯度。在制定充气方案时,应根据固体循环流率确定立管压降,补充合适气体量以维持气体下行速度均衡,使得各段的平均压力梯度相同,以单位高度充入相同气量为宜。如果立管充气量与固体循环流率不匹配或者充气分布不当,有可能导致立管运行不稳定。对于如何确定合理的充气方案将是下一步需要研究的重点。
4 结 论
采用CPFD方法对密相输运床返料系统的气固流动特性进行了数值模拟,获得如下结论:
(1)对工况1模拟得到的立管压力分布和固体循环流率结果与实验值吻合较好,表明CPFD方法能有效用于立管内非流化颗粒流动的模拟。参数敏感性分析结果表明曳力模型和颗粒最大堆积浓度对模拟结果有较大影响。
(2)对不同充气条件下立管气固流动行为进行了模拟,获得了立管压力分布和固体循环流率随充气量的变化规律,并且与实验结果的变化趋势一致。立管充气口处压力梯度绝对值为局部最大值;立管充气口气量为零时,会使充气口上方较长一段的压力梯度绝对值较小;充气增大到一定量时才会在充气口附近形成明显的气泡。
(3)立管充气的作用不只是松动颗粒,更大的作用是在立管内形成较均匀的压力梯度分布。立管底部维持高的负压力梯度流动容易形成气相逆流区,破坏颗粒稳定下落。在制定充气方案时,应根据固体循环流率确定立管压降,补充合适气体量以维持气体下行速度均衡,使得各段的平均压力梯度相同。
(4)合理的立管充气能使返料系统固体循环流率增大,但是在充气口附近易产生急剧变化的压力梯度。对于实际的工业装置,立管直径和料位高度都相对大很多,为了使压力梯度分布更为均匀,应该沿立管轴向和周向增加充气口的数量。CPFD方法可以应用到工业装置的气固流动数值模拟,本文的研究结果对高料位立管的设计与运行也有一定的指导作用。
[1] LUDLOW J C, PANDAY R, SHADLE L J. Standpipe models for diagnostics and control of a circulating fluidized bed [J]. Powder Technology, 2013, 242: 51-64.
[2] BASU P, CHENG L. An analysis of loop seal operations in a circulating fluidized bed [J]. Chemical Engineering Research and Design, 2000, 78(7): 991-998.
[3] KIM S W, NAMKUNG W, KIM S D. Solid recycle characteristics of loop-seals in a circulating fluidized bed [J]. Chemical EngineeringTechnology, 2001, 24(8): 843-849.
[4] LEUNG L S, JONES P J, KNOWLTON T M. An analysis of moving-bed flow of solids down standpipes and side valves [J]. Powder Technology, 1978, 19(1): 7-15.
[5] 张济宇, 杨贵林, 杨守扑, 等. 负压差移动床的气-固流动[J]. 化工学报, 1980, 31(3): 229-240. CHANG G Y, YANG G L, YANG S P,. Gas solid flow in a moving bed under negative pressure difference [J]. Journal of Chemical Industry and Engineering (China), 1980, 31(3): 229-240.
[6] 李洪钟. 立管移动床气固流动相图及理想料封状态[J]. 化学工程, 1989, 17(5): 28-34. LI H Z. Gas-particle flow phase-diagram and the ideal sealing state for vertical moving bed [J]. Chemical Engineering, 1989, 17(5): 28-34.
[7] NIKOLPOULOS A, NIKOLPOULOS N, VARVERIS N,. Investigation of proper modeling of very dense granular flows in the recirculation system of CFBs [J]. Particuology, 2012, 10(6): 699-709.
[8] LI T, DIETIKER J F, SHADLE L. Comparison of full-loop and riser-only simulations for a pilot-scale circulating fluidized bed riser [J]. Chemical Engineering Science, 2014, 120: 10-21.
[9] TSUJI Y, KAWAGUCHI T, TANAKA T. Discrete particle simulation of two-dimensional fluidized bed [J]. Powder Technology, 1993, 77(1): 79-87.
[10] SNIDER D M. Three fundamental granular flow experiments and CPFD predictions [J]. Powder Technology, 2007, 176(1): 36-46.
[11] 王庆功, 汪佩宁, 杨海瑞, 等. N阀和U阀内流动结构比较的数值模拟[J]. 锅炉技术, 2013, 44(5): 22-26.WANG Q G, WANG P N, YANG H R,. Comparison of the gas-solid flow characteristics between an N loop-seal and U loop-seal with numerical simulation [J]. Boiler Technology, 2013, 44(5): 22-26.
[12] 赵伟, 陆海峰, 郭晓镭, 等. CPFD在细颗粒料仓下料中的应用[J]. 化工学报, 2015, 66(2): 512-521. ZHAO W, LU H F, GUO X L,. Application of CPFD in hopper discharge of fine granular material [J]. CIESC Journal, 2015, 66(2): 512-521.
[13] ABBASI A, ISLAM M A, EGE P E. CPFD flow pattern simulation in downer reactors [J]. AIChE Journal, 2013, 59(5): 1635-1647.
[14] JIANG Y, QIU G, WANG H. Modelling and experimental investigation of the full-loop gas-solid flow in a circulating fluidized bed with six cyclone separators [J]. Chemical Engineering Science, 2014, 109: 85-97.
[15] ANDREW M J, O’ROURKE P J. The multiphase particle-in-cell (MP-PIC) method for dense particulate flows [J]. International Journal of Multiphase Flow, 1996, 22(2): 379-402.
[16] SNIDER D M. An incompressible three dimensional multiphase particle-in-cell model for dense particle flows [J]. Journal of Computational Physics, 2001, 170(2): 523-549.
[17] O'ROURKE P J, SNIDER D M. A new blended acceleration model for the particle contact forces induced by an interstitial fluid in dense particle/fluid flows [J]. Powder Technology, 2014, 256: 39-51.
[18] O’ROURKE P J, SNIDER D M. An improved collision damping time for MP-PIC calculations of dense particle flows with applications to polydisperse sedimenting beds and colliding particle jets [J]. Chemical Engineering Science, 2010, 65(22): 6014-6028.
[19] WEN C, YU Y. Mechanics of fluidization [J]. Chem. Eng. Prog. Symp. Ser., 1966, 62: 1100-1111.
[20] ERGUN S. Fluid flow through packed columns [J]. Chemical Engineering Progress, 1952, 48(2): 89-94.
[21] YIN S, ZHONG W, JIN B,. Modeling on the hydrodynamics of pressurized high-flux circulating fluidized beds (PHFCFBs) by Eulerian-Lagrangian approach [J]. Powder Technology, 2014, 259: 52-64.
[22] SOLNORDAL C B, KENCHE V, HADLEY T D,. Simulation of an internally circulating fluidized bed using a multiphase particle-in-cell method [J]. Powder Technology, 2015, 274: 123-134.
[23] WANG Q, YANG H, WANG P,. Application of CPFD method in the simulation of a circulating fluidized bed with a loop seal (Ⅰ): Determination of modeling parameters [J]. Powder Technology, 2014, 253: 814-821.
Numerical simulation of gas-solid flow in recirculation system of dense transport bed under different aerating conditions
MA Qiao1,2,3, LEI Fulin2,3, ZHANG Yawen1,2,3, YANG Shaojun2,3, XU Xiang2,3, XIAO Yunhan2,3
(1University of Chinese Academy of Sciences, Beijing 100049, China; 2Key Laboratory of Advanced Energy and Power, Institute of Engineering Thermophysics, Chinese Academy of Sciences, Beijing 100190, China; 3Research Center for Clean Energy and Power, Chinese Academy of Sciences, Lianyungang 222069, Jiangsu, China)
Computational particle fluid dynamics (CPFD) approach was employed to investigate the gas-solid flow behavior in the recirculation system of the dense transport bed. The influences of the drag model and the particle close packing limit on the simulation results were analyzed, and the appropriate model parameters were determined. Through the comparison of the simulation results under three operation conditions, the variation trends of the pressure distribution and solids circulating rate with the aeration flowrate were obtained, which was in agreement with experimental observation. The pressure gradient distribution, the gas flow direction and the solids concentration distribution were analyzed. The absolute value of the pressure gradient at the aeration inlet was the local maximum. When the aeration flowrate was zero, the pressure gradient was close to zero in a big area above the inlet. When the aeration flowrate was big enough, there was bubble around the inlet. A high pressure gradient would be formed in the lower area of the standpipe due to the lack of aeration at higher elevation, which would slow down the solids moving. The role of aeration gas on loosening particles just existed in a limited region near the inlet and its role on uniform pressure gradient distribution was more important to enable uniform gas-solid flow in the standpipe. In the design of aeration conditions, the standpipe pressure drop was determined by the solids circulating flowrate, and it needed appropriate aeration to keep constant gas velocity, leading to more uniform pressure gradient in the standpipe.
recirculation system; moving bed; numerical simulation; gas-solid two-phase flow
date: 2016-07-01.
Prof. LEI Fulin, leifulin@iet.cn
10.11949/j.issn.0438-1157.20160896
TK 227
A
0438—1157(2016)12—4959—10
中国科学院战略性先导科技专项项目(XDA07050500)。
supported by the Strategic Priority Research Program of Chinese Academy of Sciences (XDA07050500).
2016-07-01收到初稿,2016-09-22收到修改稿。
联系人:雷福林。第一作者:马乔(1986—),男,博士研究生。

